旅行商问题以及swap-2opt应用

问题简化

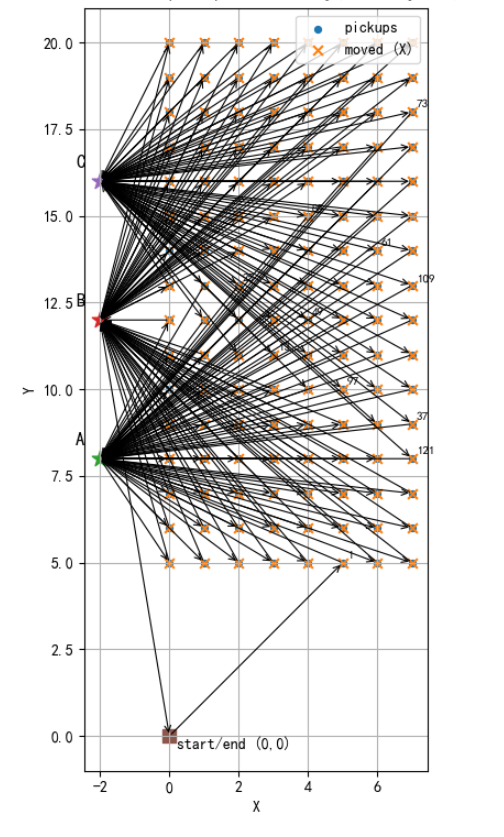
有一个花田（grid 上的 128 个点 = pickups）。

每采一朵花要送到 左侧三个点 A、B、C，循环交替送。

起点/终点是 depot = (0,0)。

要求找到一条路径，总路程最短。

这本质上是一个 变种的旅行商问题 (TSP)，带有“取点 -> 送点”的周期性约束。

初始解构造

贪心算法：每次从当前点选择最近的 pickup + 对应 delivery 的花。

得到一个 初始可行解，但不一定最优。

局部优化算子

两个典型启发式：

交换 (swap)：交换两个 pickup 顺序。

用 delta_swap 只重算局部路径，而不是全局。

2-opt：翻转一段路径。

用 delta_2opt 快速算差值。

这种 增量更新 (incremental evaluation) 能显著提高效率。

详细数学与实现解析（swap + 2-opt + 增量更新）

符号与问题建模

• 设采花点集合为 P={p1,…,pn}P=\{p_1,\dots,p_n\}P={p1​,…,pn​}（代码中 n=N=128）。

• 送货点（左侧）有三个固定位置 $D_0,D_1,D_2$（代码里的 A/B/C）。

• 起点/终点（depot）为 $s$。

• 我们用排列（permutation） $\pi$ 表示“按顺序访问 pickups 的索引”：

  π:{0,1,…,n−1}→P,位置 t上的 pickup 是 pπ(t).\pi:\{0,1,\dots,n-1\}\to P,\quad \text{位置 }t\text{ 上的 pickup 是 }p_{\pi(t)}. π:{0,1,…,n−1}→P,位置 t 上的 pickup 是 pπ(t)​.

• 距离函数用欧氏距离 $d(x,y)=\Vert x-y{\Vert }_2$。

路径的约定（和代码一致）：

s -> p_{π(0)} -> D_{0} -> p_{π(1)} -> D_{1} -> p_{π(2)} -> D_{2} -> p_{π(3)} -> D_{0} -> ...
... -> p_{π(n-1)} -> D_{(n-1) mod 3} -> s

---

完整代价函数（公式）

总路程（目标函数）对一个排列 $\pi$ 定义为

$$C(\pi )=d(s,p_{\pi (0)})+\sum _{t=0}^{n-1}(d(p_{\pi (t)},D_{t\mathrm{mod}3})+\{\begin{array}{ll}d(D_{t\mathrm{mod}3},p_{\pi (t+1)})& t<n-1\\ d(D_{t\mathrm{mod}3},s)& t=n-1\end{array}).$$

为了推导增量，我们常把 $C(\pi )$ 写成各位置的“位置贡献”之和：
令 $c_p(\pi )$ 为位置 $p$ 的贡献：

$$\begin{array}{rl}{c}_p(\pi )& =1_{p=0}d(s,p_{\pi (p)})+d(p_{\pi (p)},D_{p\mathrm{mod}3})\\ & +1_{p<n-1}d(D_{p\mathrm{mod}3},p_{\pi (p+1)})+1_{p=n-1}d(D_{p\mathrm{mod}3},s).\end{array}$$

于是

$$C(\pi )=\sum _{p=0}^{n-1}{c}_p(\pi ).$$

这就是代码中 position_contribution(perm, p) 的数学对应。

---

预计算（加速技巧）

代码在开始时预计算并保存了这些表（均为 O(1) 查询）：

• $D_{s\to p_j}=d(s,p_j)$ —— dist_depot_to_pickup[j]
• $D_{p_i\to D_r}=d(p_i,D_r)$ —— dist_pickup_to_delivery[i][r]
• $D_{D_r\to p_j}=d(D_r,p_j)$ —— dist_delivery_to_pickup[r][j]
• $D_{D_r\to s}=d(D_r,s)$ —— dist_delivery_to_depot[r]
• （可选）$D_{p_i\to p_j}$ 整表 —— dist_pickup_to_pickup[i][j]

优点：位置贡献 $c_p$ 以及各种边的代价都能用常数时间查表得到，不用每次算 sqrt。

---

邻域操作（swap / 2-opt）数学定义

• swap(a,b)：交换排列中两个位置 $a$ 和 $b$ 上的元素：

  $${\pi }^{\prime }\text{ 与 }\pi \text{ 相同，除了 }{\pi }^{\prime }(a)=\pi (b),{\pi }^{\prime }(b)=\pi (a).$$

• 2-opt(i,j)（在此语境是区间反转）：将区间 $[i,j]$ 内的顺序翻转：

  $${\pi }^{\prime }=(\pi (0),\dots ,\pi (i-1),\pi (j),\pi (j-1),\dots ,\pi (i),\pi (j+1),\dots ).$$

这些是常见的局部搜索邻域：swap 改变两个位置，2-opt 翻转一个段。

---

为什么要做“增量更新”？

如果每次候选解都完全重新计算 $C({\pi }^{\prime })$（遍历全部 $n$ 个位置），代价为 $O(n)$。做大量局部尝试（上万次）时开销太大。

增量更新的思想是：只有少量位置的贡献会因为一次邻域变换而改变，只重算这些受影响的位置即可，节省大量计算。

---

增量差值（delta）推导 —— 一般形式

对任意一次变换（swap 或 2-opt），令 ${\pi }^{\prime }$ 为变换后的排列，定义差值

$$\Delta =C({\pi }^{\prime })-C(\pi )=\sum _{p\in S}(c_p({\pi }^{\prime })-c_p(\pi )),$$

其中 $S$ 是需要重新计算的“受影响位置”集合（对其他位置，位置上与它相邻或引用的元素都没变，故贡献相同）。

下面说明每种操作的 $S$。

---

swap(a,b) 的 $S$

记 $a<b$。交换 $\pi (a)$ 和 $\pi (b)$ 只影响这些位置的贡献：

S⊆{a−1,a,a+1,b−1,b,b+1}∩{0,…,n−1}.S \subseteq \{a-1,a,a+1,\, b-1,b,b+1\}\cap\{0,\dots,n-1\}. S⊆{a−1,a,a+1,b−1,b,b+1}∩{0,…,n−1}.

直观理由：位置 $p$ 的贡献 $c_p$ 只参照位置 $p$ 的元素和（若 $p<n-1$）位置 $p+1$ 的元素，以及 $p-1$ 的元素可能指向它（在 $c_{p-1}$ 中）。因此，只有被交换元素所在位置及其相邻位置会改变。

代码里就是按这个集合重算旧贡献与新贡献的和（见 delta_swap）。

边界/特殊情况：若 $b=a+1$（相邻交换），集合更小，但上面的一般集合仍然覆盖（某些索引会重复或不存在，但代码用集合并排除越界）。

---

2-opt(i,j) 的 $S$

反转区间 $[i,j]$ 会使区间内每个位置的元素都换到新的位置，因此所有 $p\in [i,j]$ 的贡献都变。并且边界位置 $i-1$ 和 $j+1$ 的贡献也会变（它们的“下一位置”或“上一位置”发生变化）。所以

S={i−1,i,i+1,…,j,j+1}∩{0,…,n−1}.S = \{i-1, i, i+1, \dots, j, j+1\}\cap\{0,\dots,n-1\}. S={i−1,i,i+1,…,j,j+1}∩{0,…,n−1}.

代码中的实现就是显式构造这个集合并重算这些位置的贡献差（见 delta_2opt）。

复杂度：2-opt 的增量开销与区间长度成正比：若区间长 $k=j-i+1$，则需要 $O(k)$ 次位置贡献计算。

---

位置贡献具体项（展开）——便于手动核对

对于位置 $p$（$0\le p\le n-1$），令元素索引 $a=\pi (p)$，若 $p<n-1$ 令后续元素 $b=\pi (p+1)$。则

$$c_p(\pi )=\{\begin{array}{ll}d(s,p_a)+d(p_a,D_{p\mathrm{mod}3})+d(D_{p\mathrm{mod}3},p_b),& p<n-1,\\ d(s,p_a)+d(p_a,D_{p\mathrm{mod}3})+d(D_{p\mathrm{mod}3},s),& p=n-1.\end{array}$$

（注意若 $p\ne 0$ 则第一个 $d(s,p_a)$ 项为 0 —— 我用前面的带指示符的写法更严谨，但这里展开便于理解实际参与的边。）

因此在编程实现中，position_contribution 只由少量查表运算组成（常数次 dist_* 查表）。

---

复杂度与性能（实际意义）

• position_contribution：常数时间 $O(1)$（查几张表）。
• delta_swap：最多重算 6 个位置，时间 $O(1)$（上界常数）。所以尝试一次随机 swap 的代价是常数的，非常快。
• delta_2opt：重算 $O(k)$ 个位置，其中 $k=j-i+1$。如果 $i,j$ 是均匀随机的，期望 $k$ 大约为 $O(n)$ 的一个常数比例（粗略期望约为 $n/3$），所以 2-opt 较 swap 更“重”一些，但仍然远比全量 $O(n)$ 重新求和快很多——因为只重算受影响的 $O(k)$ 位置而不是全体 $n$。

总体局部搜索流程（伪代码）：

while time_remaining:if coin_flip < 0.5:pick random i,jΔ = delta_swap(perm,i,j)if Δ < 0: accept swap (perm updated, cost += Δ)else:pick random i<jΔ = delta_2opt(perm,i,j)if Δ < 0: accept 2-opt (reverse segment)

（代码中用 d < -1e-12 作为改进判定以避免浮点噪声。）

---

数值示例（小规模，便于手算验证）

用一个 $n=4$ 的小例子演示：

• depot $s=(0,0)$
• pickups： $p_0=(1,0),p_1=(2,0),p_2=(3,0),p_3=(4,0)$
• deliveries： $D_0=(0,1),D_1=(0,2),D_2=(0,3)$

用代码按上述 C(π)、delta_swap、delta_2opt 定义计算得到（这是我内部计算的结果）：

dist_depot_to_pickup: [1.0, 2.0, 3.0, 4.0]
dist_pickup_to_delivery matrix:
[1.41421356, 2.23606798, 3.16227766]
[2.23606798, 2.82842712, 3.60555128]
[3.16227766, 3.60555128, 4.24264069]
[4.12310563, 4.47213595, 5.0]
dist_delivery_to_pickup matrix:
[1.41421356, 2.23606798, 3.16227766, 4.12310563]
[2.23606798, 2.82842712, 3.60555128, 4.47213595]
[3.16227766, 3.60555128, 4.24264069, 5.0]
dist_delivery_to_depot: [1.0, 2.0, 3.0]初始排列 perm = [0,1,2,3]
old_cost = 25.450006尝试 swap(1,3):delta_swap = +0.24926   (表示变差了，路径变长 0.24926)new_cost = 25.699266 = old_cost + delta尝试 2-opt(1,3) (把区间 [1,3] 反转):delta_2opt = +0.24926   （与上面的 swap 在此例中产生相同的差值）new_perm = [0,3,2,1], new_cost = 25.699266

还可以看受影响位置的贡献值（交换前后）：

受影响位置: [0,1,2,3]
旧贡献: [4.650282, 6.433978, 9.242641, 5.123106]
新贡献: [6.537319, 8.077687, 7.848192, 3.236068]
差值合计 = +0.24926

这个例子说明：用 delta 函数只计算受影响位置（在例子里是 4 个位置），就足够知道整个代价的变化，而不需要重新计算全部位置。

---

代码实现里的若干关键细节（对正确性/稳定性很重要）

• 为什么 S={a-1,a,a+1,b-1,b,b+1} 足够？
  因为一个位置 $p$ 的贡献只依赖于：位置 $p$ 的元素、位置 $p+1$ 的元素（用于下一跳），以及位置 $p-1$ 的元素会在 $c_{p-1}$ 中引用 $p$ 的元素。因此，只有被交换元素本身和它们的左右邻居会引用或被引用——其它位置不受影响。

• 边界条件：代码在构造 affected 时做了越界检查（if 0 <= p < n），处理 $p=0$（有 depot->pickup 项）和 $p=n-1$（有 delivery->depot 项）两种特殊边。

• 浮点容忍阈值：d < -1e-12 用来避免因为浮点四舍五入做出不必要的微小变更。

• 随机选择策略：代码在 swap/2-opt 之间 50/50 随机选择；这只是简单元启发，也可以用更复杂的策略（比如优先尝试较大改进的候选，或加上模拟退火的概率接受上升解）来跳出局部最优。

• 记录历史：每隔 log_interval 或出现改进时将 (iteration, cost, route) 记录到 history。这既用于分析收敛，也便于画图或回溯最优解。

---

# modified_route_solver.py
# Requires: matplotlib. Optional: ortools for the approx ATSP step.
import math
import random
import sys
import time
import csv
import matplotlib.pyplot as plt# --- build points ---
# pickups (flowers) grid
pickups = [(x, y) for x in range(0, 8) for y in range(5, 21)]  # 8 x 16 = 128
N = len(pickups)# left positions A,B,C
A = (-2, 8)
B = (-2, 12)
C = (-2, 16)
deliveries_positions = [A, B, C]# start/end
depot = (0, 0)# --- Precompute distances to avoid repeated hypot calls ---
def euclid(a, b):return math.hypot(a[0]-b[0], a[1]-b[1])# dist matrices
dist_depot_to_pickup = [euclid(depot, p) for p in pickups]                # depot -> pickup_j
dist_pickup_to_delivery = [[euclid(pickups[i], deliveries_positions[r]) for r in range(3)] for i in range(N)]
dist_delivery_to_pickup = [[euclid(deliveries_positions[r], pickups[j]) for j in range(N)] for r in range(3)]
dist_delivery_to_depot = [euclid(deliveries_positions[r], depot) for r in range(3)]
dist_pickup_to_pickup = [[euclid(pickups[i], pickups[j]) for j in range(N)] for i in range(N)]# --- helper to compute full route cost given a permutation ---
def full_route_cost_from_permutation(perm):cost = dist_depot_to_pickup[perm[0]]  # depot -> first pickupfor t, idx in enumerate(perm):r = t % 3cost += dist_pickup_to_delivery[idx][r]  # pickup -> delivery_rif t < len(perm) - 1:next_idx = perm[t+1]cost += dist_delivery_to_pickup[r][next_idx]else:cost += dist_delivery_to_depot[r]  # last delivery -> depotreturn cost# --- greedy constructive initial permutation ---
def greedy_initial_permutation():remaining = set(range(N))perm, current_pos_is_depot, t = [], True, 0while remaining:best, best_cost = None, float('inf')r = t % 3if current_pos_is_depot:for idx in remaining:c = dist_depot_to_pickup[idx] + dist_pickup_to_delivery[idx][r]if c < best_cost:best_cost, best = c, idxelse:for idx in remaining:c = dist_delivery_to_pickup[(t-1) % 3][idx] + dist_pickup_to_delivery[idx][r]if c < best_cost:best_cost, best = c, idxperm.append(best)remaining.remove(best)current_pos_is_depot, t = False, t + 1return perm# --- incremental/local cost helpers ---
def position_contribution(perm, p):i, r, c = perm[p], p % 3, 0.0if p == 0:c += dist_depot_to_pickup[i]c += dist_pickup_to_delivery[i][r]if p < len(perm) - 1:j = perm[p+1]c += dist_delivery_to_pickup[r][j]else:c += dist_delivery_to_depot[r]return cdef delta_swap(perm, i, j):if i == j: return 0.0n = len(perm)a, b = min(i, j), max(i, j)affected = {p for p in [a-1, a, a+1, b-1, b, b+1] if 0 <= p < n}old = sum(position_contribution(perm, p) for p in affected)new_perm = perm[:]new_perm[a], new_perm[b] = new_perm[b], new_perm[a]new = sum(position_contribution(new_perm, p) for p in affected)return new - olddef delta_2opt(perm, i, j):n = len(perm)affected = set(range(max(0, i-1), min(n-1, j+1)+1))affected.update(range(i, j+1))old = sum(position_contribution(perm, p) for p in affected)new_perm = perm[:i] + list(reversed(perm[i:j+1])) + perm[j+1:]new = sum(position_contribution(new_perm, p) for p in affected)return new - old# --- local improvement: randomized swap + 2-opt ---
def improve_permutation(perm, time_limit=20.0, log_interval=1000):best_perm, best_cost = perm[:], full_route_cost_from_permutation(perm)start_time, it = time.time(), 0history = [(0, best_cost, best_perm[:])]while time.time() - start_time < time_limit:it += 1if random.random() < 0.5:i, j = random.sample(range(N), 2)d = delta_swap(best_perm, i, j)if d < -1e-12:best_perm[i], best_perm[j] = best_perm[j], best_perm[i]best_cost += delse:i = random.randrange(0, N-1)     # FIXED: 不会取到 N-1j = random.randrange(i+1, N)     # 确保 j > id = delta_2opt(best_perm, i, j)if d < -1e-12:best_perm[i:j+1] = list(reversed(best_perm[i:j+1]))best_cost += dif it % log_interval == 0 or d < -1e-12:history.append((it, best_cost, best_perm[:]))return best_perm, best_cost, history# --- try OR-Tools (optional) ---
use_ortools = True
try:from ortools.constraint_solver import pywrapcp, routing_enums_pb2
except Exception:use_ortools = Falseprint("OR-Tools not available; using heuristic only.", file=sys.stderr)# --- Main program ---
random.seed(1)
init_perm = greedy_initial_permutation()
init_cost = full_route_cost_from_permutation(init_perm)
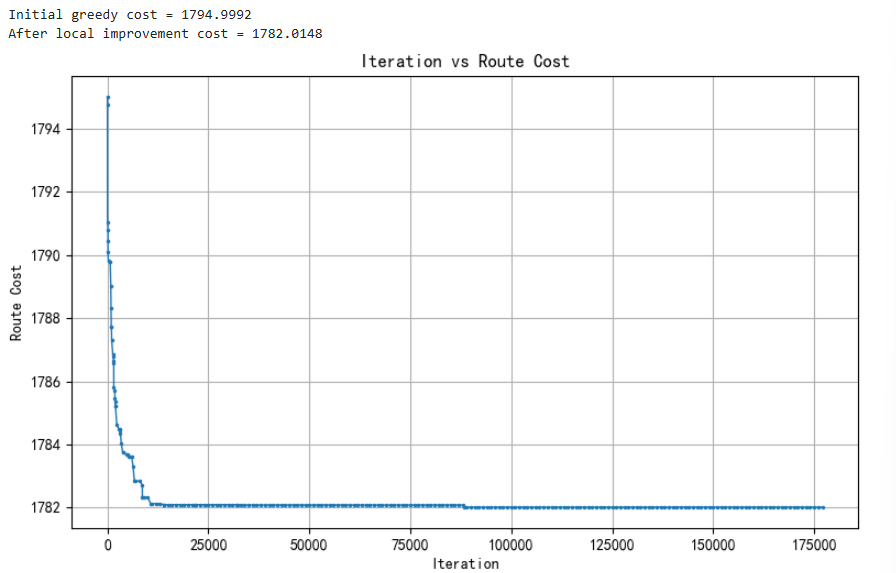
print(f"Initial greedy cost = {init_cost:.4f}")# Improve with local randomized search
perm, cost_after_improve, history = improve_permutation(init_perm, time_limit=8.0, log_interval=1000)
print(f"After local improvement cost = {cost_after_improve:.4f}")# Save history to CSV
with open("route_history.csv", "w", newline="") as f:writer = csv.writer(f)writer.writerow(["iteration", "cost", "route"])for it, cost, route in history:coords = [pickups[idx] for idx in route]writer.writerow([it, f"{cost:.4f}", coords])# Plot iteration vs cost
its, costs = zip(*[(it, cost) for it, cost, _ in history])
plt.figure(figsize=(8,5))
plt.plot(its, costs, marker=".", linewidth=1, markersize=3)
plt.xlabel("Iteration")
plt.ylabel("Route Cost")
plt.title("Iteration vs Route Cost")
plt.grid(True)
plt.tight_layout()
plt.show()# --- Build full path for plotting ---
path_coords = [depot]
picked_indices = []
for t, idx in enumerate(perm):path_coords.append(pickups[idx])picked_indices.append(idx)dpos = deliveries_positions[t % 3]path_coords.append(dpos)
path_coords.append(depot)# moved pickups set
moved = set(picked_indices)# Plot final route
plt.figure(figsize=(10,9))
xs, ys = zip(*pickups)
plt.scatter(xs, ys, s=18, label="pickups")
mx = [pickups[i][0] for i in moved]
my = [pickups[i][1] for i in moved]
plt.scatter(mx, my, marker='x', s=40, label="moved (X)")
for lab, pos in zip(['A', 'B', 'C'], [A, B, C]):plt.scatter([pos[0]], [pos[1]], s=120, marker='*')plt.text(pos[0]-0.7, pos[1]+0.4, lab, fontsize=12, weight='bold')
plt.scatter([depot[0]], [depot[1]], s=80, marker='s')
plt.text(depot[0]+0.2, depot[1]-0.4, 'start/end (0,0)', fontsize=10)
for i in range(len(path_coords)-1):x0,y0 = path_coords[i]x1,y1 = path_coords[i+1]plt.annotate("", xy=(x1,y1), xytext=(x0,y0), arrowprops=dict(arrowstyle="->", linewidth=0.8))
for seq_index, pickup_idx in enumerate(perm):if seq_index % 12 == 0:x,y = pickups[pickup_idx]plt.text(x+0.12, y+0.12, str(seq_index+1), fontsize=8)
plt.title("Route visualization: start -> pickup -> delivery(A/B/C cyclic) -> ... -> return")
plt.xlabel("X")
plt.ylabel("Y")
plt.gca().set_aspect("equal", adjustable="box")
plt.grid(True)
plt.legend(loc="upper right")
plt.show()# Print summary
print("Summary:")
print(f"Number of pickups: {N}")
print(f"Final route total Euclidean distance: {cost_after_improve:.4f}")
print("First 12 pickups and deliveries (A/B/C):")
for i in range(min(12, len(perm))):print(i+1, perm[i], "pickup_coord=", pickups[perm[i]], "delivery=", deliveries_positions[i % 3])