数据结构与算法（栈）

栈

栈的定义及特点

栈（Stack）是操作限定在表的一端进行的线性表。

允许进行插入、删除等操作的一端称为栈顶（Top）。另一端是固定的，不允许插入和删除，称为栈底（Bottom）。向栈中插入一个新元素称为入栈（或压栈），从栈中删除一个元素称为出栈（或退栈）。

栈通常记为：S = (a1，a2，…，an)，a1为栈底元素，an为栈顶元素。当栈中没有数据元素时称为空栈（Empty Stack）。n个数据元素按照a1，a2，…，an的顺序依次入栈，而出栈的次序相反，an第一个出栈，a1最后一个出栈。所以，栈的操作是按照后进先出（Last In FirstOut，简称LIFO）或先进后出（First In Last Out，简称FILO）的原则进行的，因此，栈又称为LIFO表或FILO表。
栈的操作示意图如图3.1所示，其中 top 为栈顶指针，用于记录栈顶元素的位置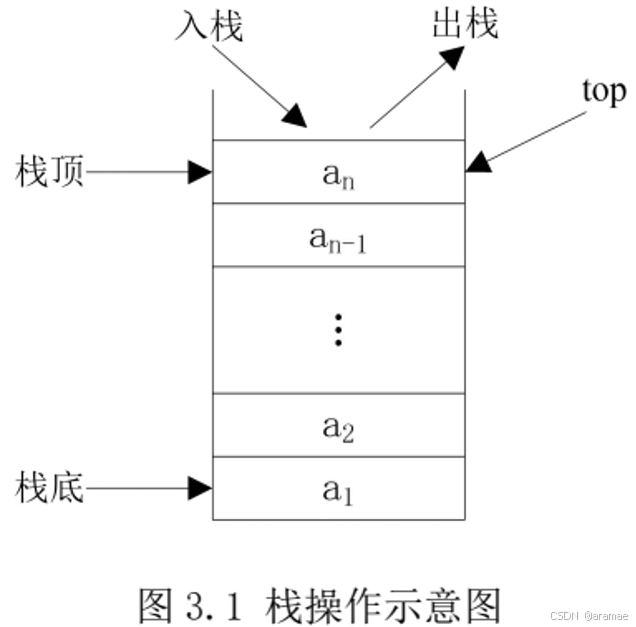

由于栈只能在栈顶进行操作，不能在栈的其他位置插入或删除元素，因此栈的操作是线性表操作的一个子集。
栈的操作主要包括在栈顶插入元素和删除元素、取栈顶元素和判断栈是否为空等。

栈的抽象数据类型定义

栈的基本操作除了入栈和出栈外， 还有栈的初始化、 栈空的判定，以及取栈顶元素等。
下面给出栈的抽象数据类型定义：ADT Stack{数据对象：D = {ai|1 ≤ i ≤ n, n ≥ 0, ai是 ElemType 类型}，D 是具有相同特性的数据元素的集合。

数据关系：R = { < ai−1，ai > |ai−1、ai ∈ D，1 ≤ i ≤ n}，约定an端为栈顶，a1端为栈底。

基本操作：

• InitStack(&s)
  初始条件：栈不存在。
  操作结果：构造一个空栈 s。

• StackEmpty(s)
  初始条件：栈 s 已存在。
  操作结果：判断栈 s 是否为空，若为空则返回 true，否则返回 false。

• Push(&s,e)
  初始条件：栈 s 已存在，e 是一个给定的待入栈的数据元素。
  操作结果：将元素 e 插入到栈 s 的顶部，作为新的栈顶元素。

• Pop(&s,&e)
  初始条件：栈 s 已存在。
  操作结果：将栈 s 的栈顶元素值赋给引用型参数 e，并出栈栈顶元素。

• GetTop(s,&e)
  初始条件：栈 s 已存在。
  操作结果：读取栈 s 中的栈顶元素，并将其值赋给 e，栈顶不发生变化。

• DestroyStack(&s)
  初始条件：栈 s 已存在。
  操作结果：释放栈 s 占用的存储空间。
  和线性表类似，栈也有两种存储表示方法，分别称为顺序栈和链栈。

顺序栈的定义

顺序栈（Sequence Stack）是用一片连续的存储空间来存储栈中的数据元素。类似于顺序表，可以用一维数组来存放顺序栈中的数据元素，用一个记录栈顶位置的整型变量（栈顶指针）来表示栈顶元素的位置。顺序栈的定义如下:

其中，top 称为栈顶指针，用于指示栈顶元素在数组中的下标值，其初值为-1，即 top=-1

顺序栈的存储形态

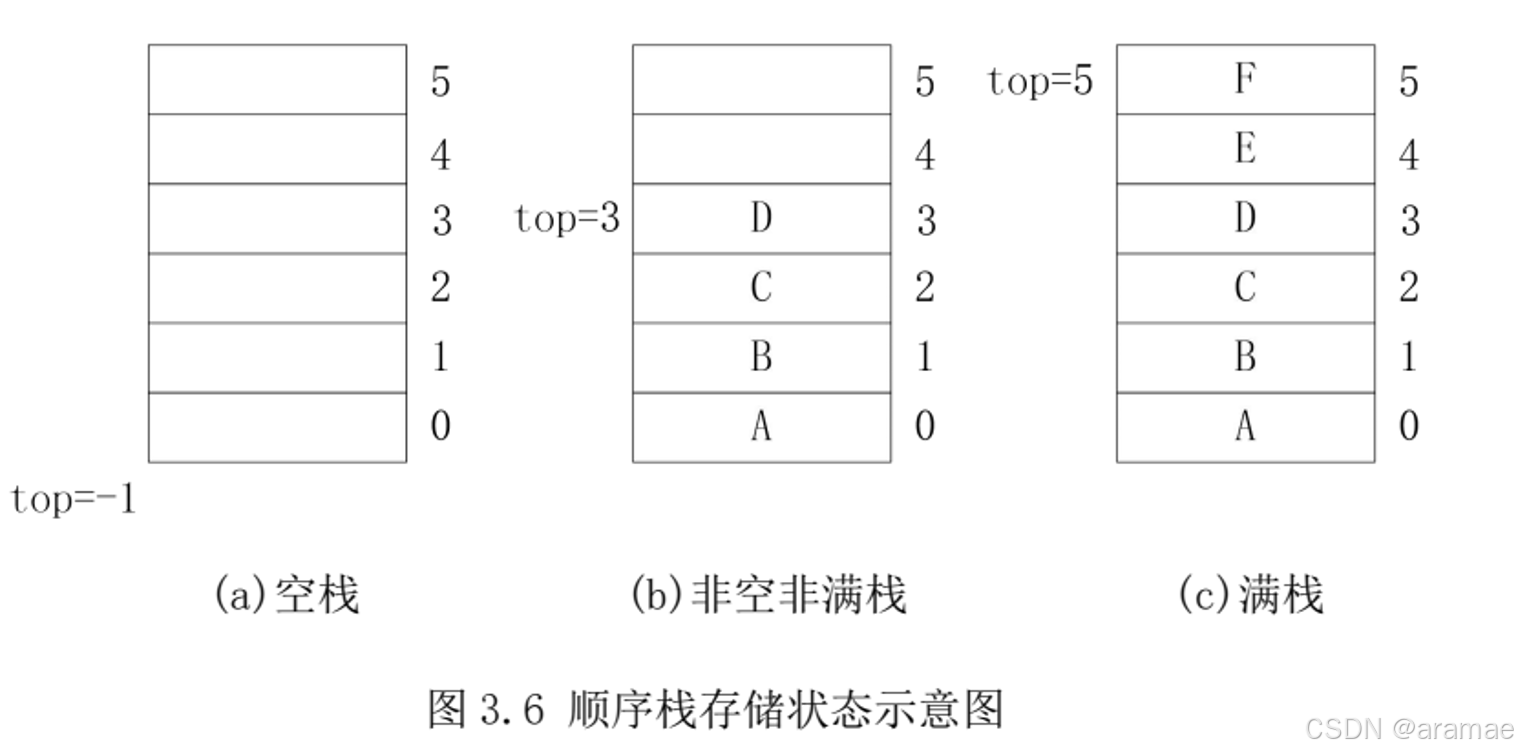
• 根据顺序栈中元素的数目和栈的容量，顺序栈存在三种形态：空栈、非空非满栈和满栈
• 如定义一个长度为 6 的顺序栈 s，将栈底设在数组底端。top 为栈顶指针，记录栈顶元素位置。

1. 图 3.6（a）中栈顶指针 top=-1，表示栈中没有任何元素，即空栈；
2. 图 3.6（b）中栈顶指针 top=3，栈顶元素为 D，A 为栈底元素，栈中一共有 A、B、C、D 4 个元素，栈的最大容量为 6，因此该栈为非空非满；
3. 图 3.6（c）中栈顶指针 top=5，即 F 为栈顶元素，栈内一共有 6 个元素，顺序栈的最大容量也为 6，栈中不能再插入任何元素，此时栈的状态为满，也可以把该顺序栈称为满栈。

顺序栈的入栈和出栈

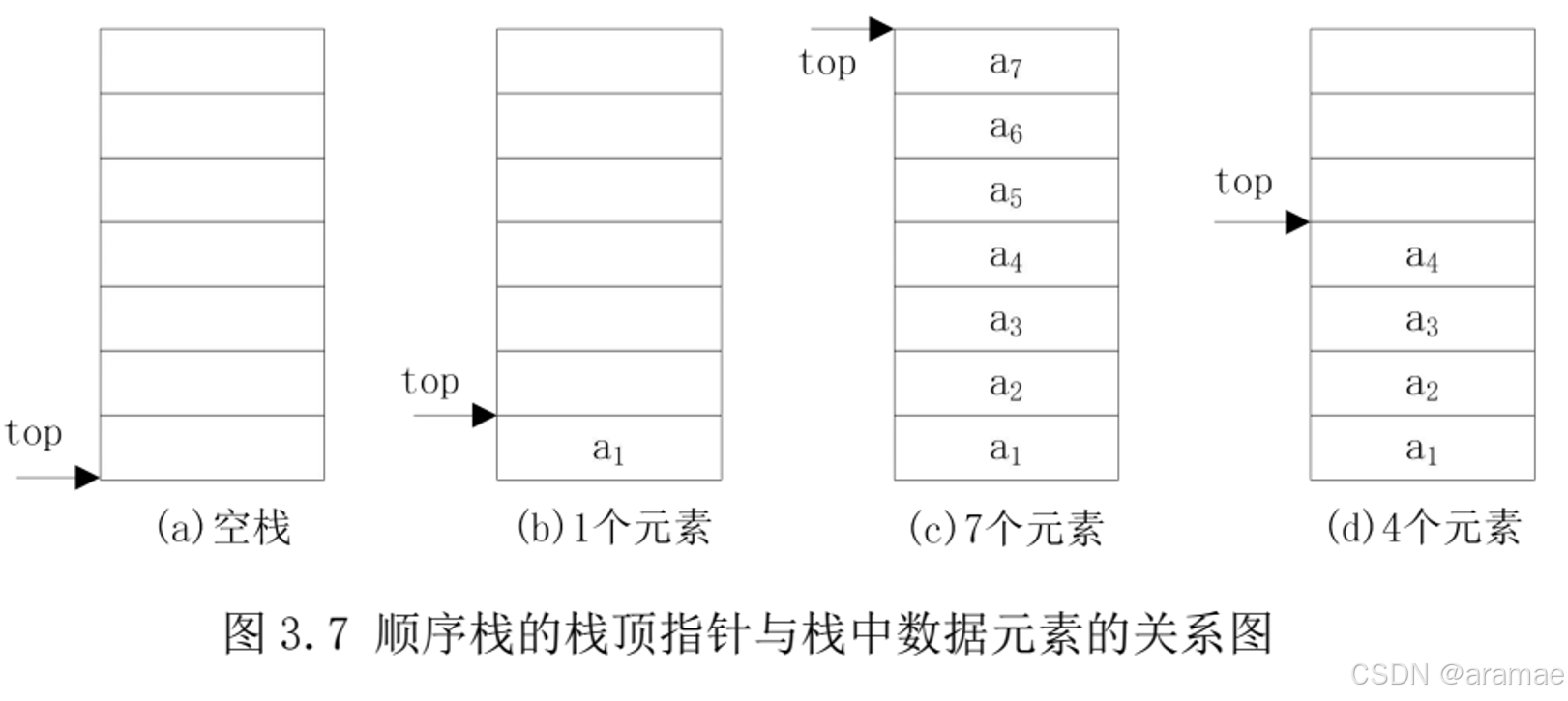
顺序栈有插入和删除两种基本操作，即入栈和出栈。下面以图3.7为例讲解顺序栈的两种操作，设定s是指向顺序栈的指针。

• 入栈操作
  图3.7（a）为空栈，进行入栈操作时只需要将栈顶指针top加1，再把元素a1存放在这个位置上
  如图3.7（b）所示。按照此操作可以实现a2,…,an的入栈操作
  如图3.7（c）所示，其核心操作为：s->top++，s->data[top]=ai。
  在图3.7（c）满栈时插入一个元素时，由于栈已满会产生溢出错误，称为上溢出。故进行入栈操作前，需要判断栈是否为满，满栈入栈产生上溢出错误

• 出栈操作
  在图3.7（c）栈中删除一个元素时只需将栈顶指针top减1，使其指向新的栈顶元素即可，按照此操作可以实现a7,a6,a5的出栈操作
  如图3.7（d）所示，其核心操作为：s->top–
  在图3.7（a）空栈时删除一个元素时，由于空栈中没有元素，会产生溢出错误，称为下溢出。故进行出栈操作前，需要检查栈是否为空，对空栈进行出栈操作时肯能产生下溢出错误

顺序栈的基本操作

1．顺序栈的初始化

创建一个空栈，由指针s指向它，并将栈顶指针top设置为-1。其算法如下：

2．判断顺序栈是否为空

如果顺序栈s的top为-1，则顺序栈为空，返回true，否则返回false。其算法如下

3．入栈操作

入栈操作是在顺序栈s未满的情况下，先使栈顶指针top加1，然后在栈顶添加一个新元素e，入栈成功返回true，否则返回false。其算法如下

4．出栈操作

出栈操作是指在栈s不为空的情况下，将栈顶元素值赋给引用型参数e，再使栈顶指针top减1，出栈成功返回true，否则返回false。其算法如下

5．读取栈顶元素

如果顺序栈s不为空，将栈顶元素值赋给引用型参数e，返回true，否则返回false。其算法如下

6．销毁顺序栈

释放顺序栈s所占用的存储空间。其算法如下

上述 6 个顺序栈基本操作的时间复杂度均为 O(1)，说明顺序栈是一种高效的算法设计。

链栈的定义

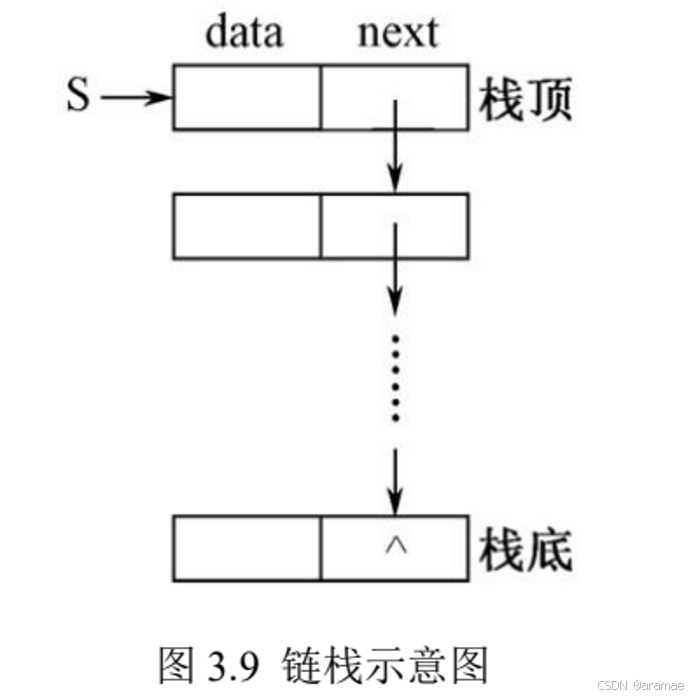
链式存储方式的栈，称为链栈（Linked Stack）。链栈通常用单链表来表示，它的实单链表的简化，如图3.9所示。
所以，链栈结点的结构与单链表结点的结构一样。
由于链栈的操作只是在一端进行，为了操作方便，把栈顶设在链表的头部。链栈的类型定义及变量说明和单链表一样，其类型定义如下：

链栈的基本操作

1．链栈的初始化

建立一个空栈s。实际上是创建链栈的头结点，并将其next域置为NULL，如图3.11所示。其算法如下：

2．判断链栈是否为空

栈s为空的条件是s->next==NULL为真，即单链表中只有头结点，没有数据结点。其算法如下

3．入栈操作

链栈的进栈步骤（无需判断是否为满栈）：

• ①为待进栈元素动态分配新结点，将新结点的首地址存入指针变量p，将e赋给新结点的数据域；
• ②将新结点的指针域指向原栈顶结点；
• ③修改头结点的指针域指向新结点，将新结点设置为栈顶结点。其算法如下
  

4．出栈操作

链栈的出栈步骤如下：

• ①检查栈是否为空，若为空，则进行“下溢出”错误处理，返回false；
• ②将栈顶指针暂存起来，以便返回调用者和释放栈顶存储空间，并保存栈顶元素值；
• ③删除栈顶结点，即将头结点指针域指向原栈顶结点的后续结点，使其成为新的栈顶结点；
• ④释放原栈顶结点的存储空间；⑤出栈成功，返回true。其算法如下

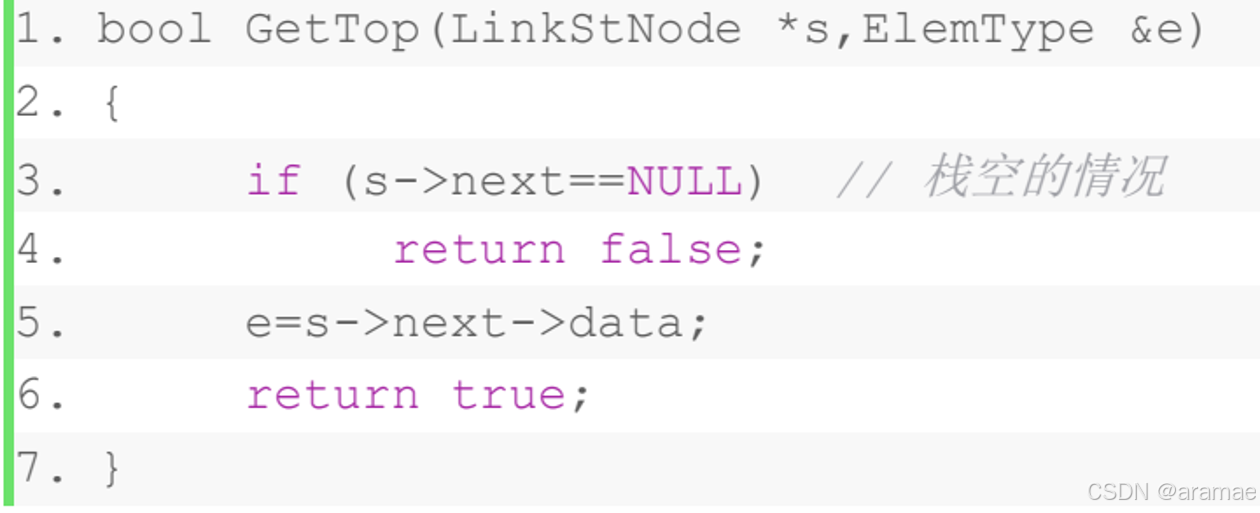
5．读取栈顶元素

读取栈顶元素步骤如下：

• ①检查栈是否为空，若为空，则进行“下溢出”错误处理，返回false；
• ②读取栈顶元素值赋给引用型参数e；
• ③读取成功，函数返回true。其算法如下：

6．销毁链栈

销毁链栈步骤如下：

• ①定义指针p指向栈顶结点；
• ②通过循环语句，依次销毁栈顶结点；
• ③最后销毁链栈的头结点。
  其算法如下

1. void DestroyStack(LinkStNode *&s)
2. {
3. LinkStNode *p = s->next;
4. while (p != NULL)
5. {
6. s->next = p->next;
7. free(p);
8. p=s->next;
9. }
10. free(s); // s 指向头结点,释放其空间
11. s = NULL;
12. }