手写数据结构-- avl树

1. 介绍

avl树是一种平衡二叉树，对于我来说手写这个树还是有一定难度的。

去年其实写过一次，但是只关注了旋转的部分而且也没有写博客记录。

于是今年重新写了一遍，发现之前的实现对于失衡情况的处理有问题。

之前对于失衡情况只处理了一次，正确的实现应该从当前节点开始一直

往父节点回溯，直到当前节点的子树重新平衡为止。

2. 旋转类型

avl是通过维护两子树高度差不超过1来保证不会出现退化的，比如说传统的二叉排序树对于有序插入1 2 3 4 5 6 这样的情况，会直接退化成链表的。

当avl树发生失衡时，就通过旋转来进行调整。

一共有四种旋转类型，不过最基础的只有两种：左旋、右旋；

剩余的旋转类型只是复合一下这两种类型：

左右旋转，就是先左旋，再右旋转。
右左旋转，就是先右旋，再左旋转。

2.1 左旋

这种情况发生在右子树高度比左子树高2，且右子树的右子树高度+1

等于右子树高度。

直接偷programiz的图来说明

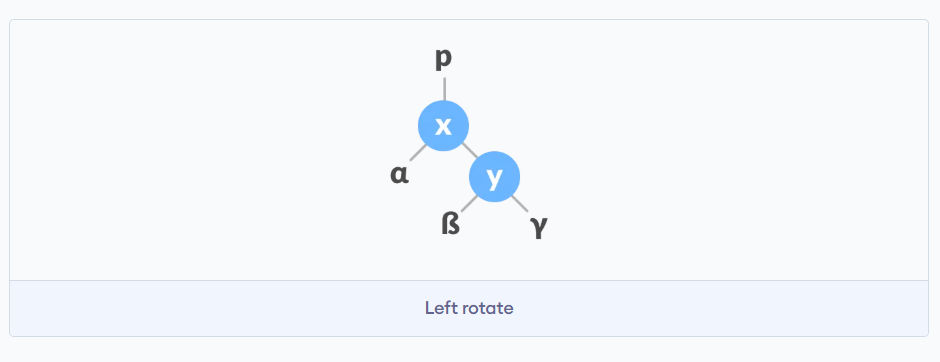
如上图所示，假设用绝对值来表示树的高度，那么发生左旋的情况就是

$$\begin{gathered} |y|-|\alpha |=2 \\ |\gamma |-|\alpha |=1 \end{gathered}$$

至于$\beta$的高度我们并不关心。

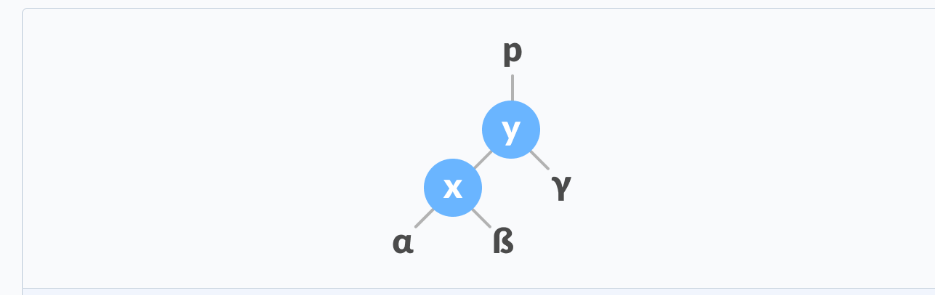
由于我们想让高度回落，因此新的树根就不能再为$x$，

而是要让$y$变成新的根。

那么$x$和它的子树$\alpha$就变成了$y$的左子树，

那$y$原来的左子树$\beta$怎么办呢，由于$\beta$肯定比$x$大，

所以让它链接在$x$的右子树上好了。

旋转后的树长下面这样，中间先后顺序的细节自己试一下就知道了。

我也不想写那么细了。

2.2 右旋

右旋就类似了，左子树的高度比右子树的高度大2。

左子树的左子树高度加一为左子树高度。

还是看图吧！

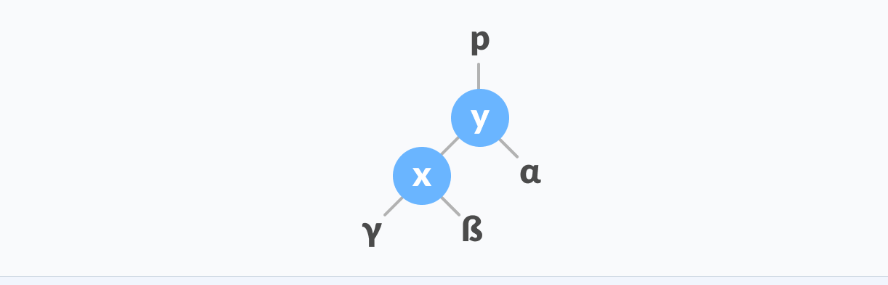
同样的表示法

$$\begin{gathered} |x|-|\alpha |=2 \\ |x|=|\gamma |+1 \end{gathered}$$
至于$\beta$子树的高度，我们不关心。

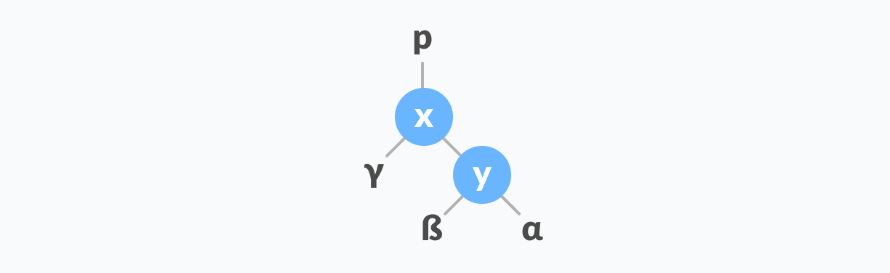
由于我们想让高度回落，因此新的树根就不能再为$y$，

而是要让$x$变成新的根。

那么$y$和它的子树$\alpha$就变成了$x$的右子树，

那$x$原来的右子树$\beta$怎么办呢，由于$\beta$肯定比$x$小，

所以让它链接在$x$的左子树上好了。

旋转后的树

2.3 左右旋

这种情况发生在左子树高度比右子树高度高$2$，

且左子树的右子树高度+1等于左子树的高度。

注意这种情况实际上是左子树失衡的另外一种情况，

只有它不是左旋的情况时，才考虑这种情况。

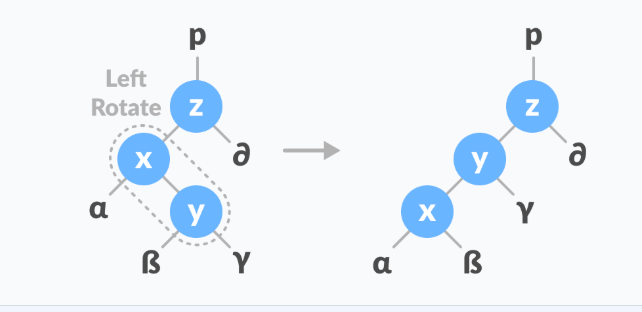
如图所示，左右旋的情况需要满足

$$\begin{gathered} |x|-|\delta |=2 \\ |y|-|\delta |=1 \\ |\alpha |=|\delta | \end{gathered}$$

先对$xy$进行左旋，再对yz右旋。

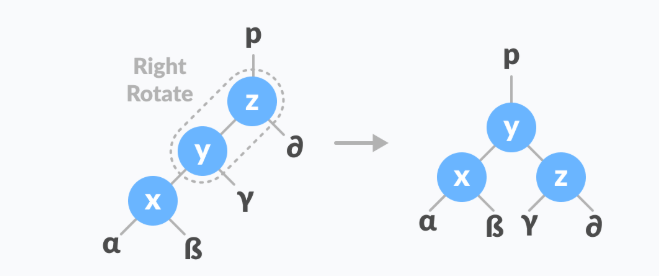
2.4 右左旋

这种情况发生在右子树高度比左子树高度高$2$，

且右子树的左子树高度+1等于右子树的高度。

注意这种情况实际上是右子树失衡的另外一种情况，

只有它不是右旋的情况时，才考虑这种情况。

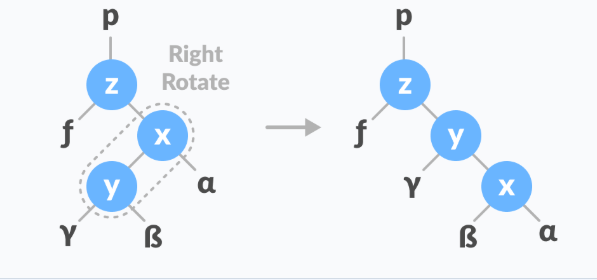
如图所示，右左旋的情况需要满足

$$\begin{gathered} |x|-|f|=2 \\ |y|+1=|x| \\ |\alpha |=|f| \end{gathered}$$

先对$xy$右旋转，再对$yz$左旋转。

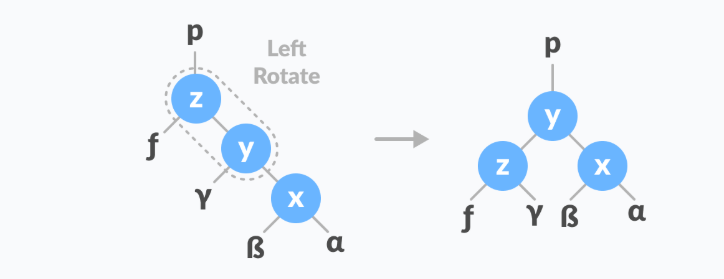
3. 删除一个节点

删除节点的实现感觉不太统一，我这里的实现是用的替换。

先找到替换的节点，

要么是左子树的最右节点，要么是右子树的最左节点。

其实就是中序遍历的前一个或者后一个节点罢了。

在完成值替换后，找到被替换节点父节点，将被替换的节点从树上

删除掉，再从这个父节点开始判断是否失衡并调整一直到根。

这里我们需要一直调整了，因为删除一个节点导致的树高度回落

有可能导致一连串的失衡！

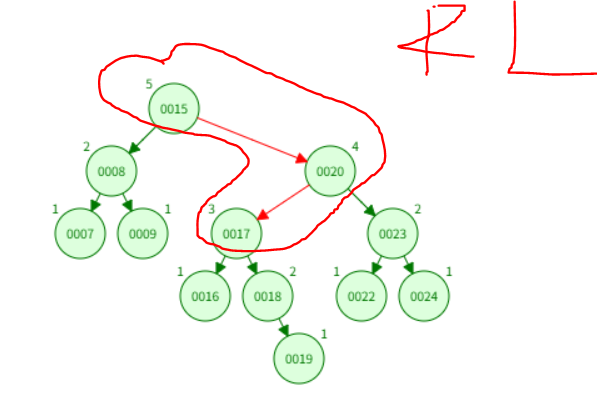
比如说下面的情况，删除了一个节点但连续调整了两次。

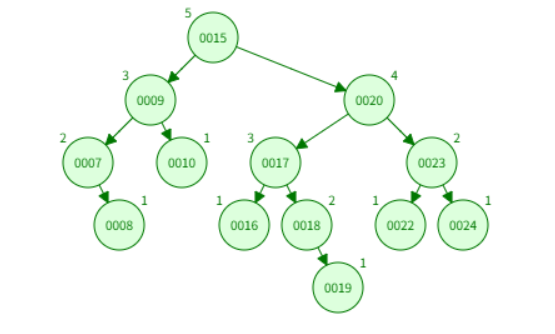
删除节点10后

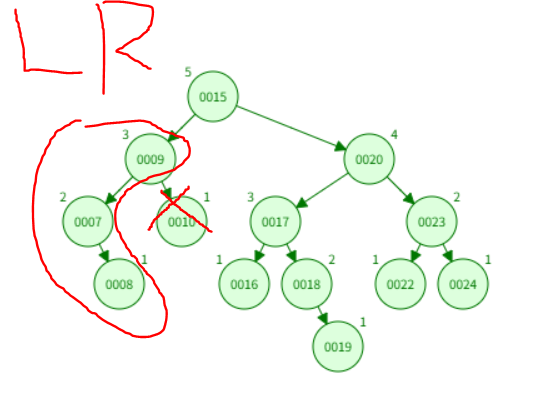
第一次调整后

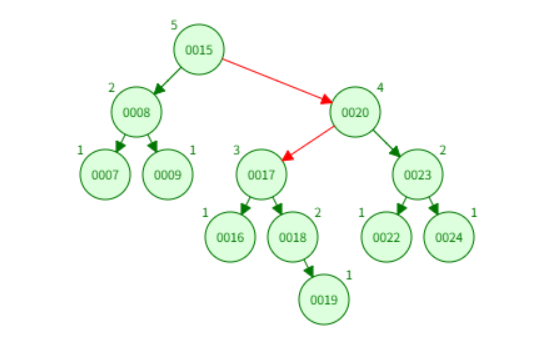
第二次调整

4. 插入一个节点

对于每个节点， 我们需要维护下面的值

struct avl_node_ {int height;int val;struct avl_node_ *lchild;struct avl_node_ *rchild;struct avl_node_ *parent;
};

插入的算法其实跟普通的二叉搜索树的插入完全一样，只不过在插入后

我们树可能失衡，我们就需要重新平衡子树。

我们在插入完成后，判断插入节点的父亲节点对对应的树是否发生了

失衡，如果失衡了就判断失衡的类型，从而决定旋转的类型来调整。

插入引起的高度最多是增加一，因此一次调整就可以使得树平衡了。

但为了省事其实可以沿用一直调整到树平衡这个函数。

5. 代码实现

放在我的gitee上了。

可以年看下参考里的第二个，它是有动画演示的。

6. 参考

prograiz
usfca