Python12-聚类算法

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

1. 介绍

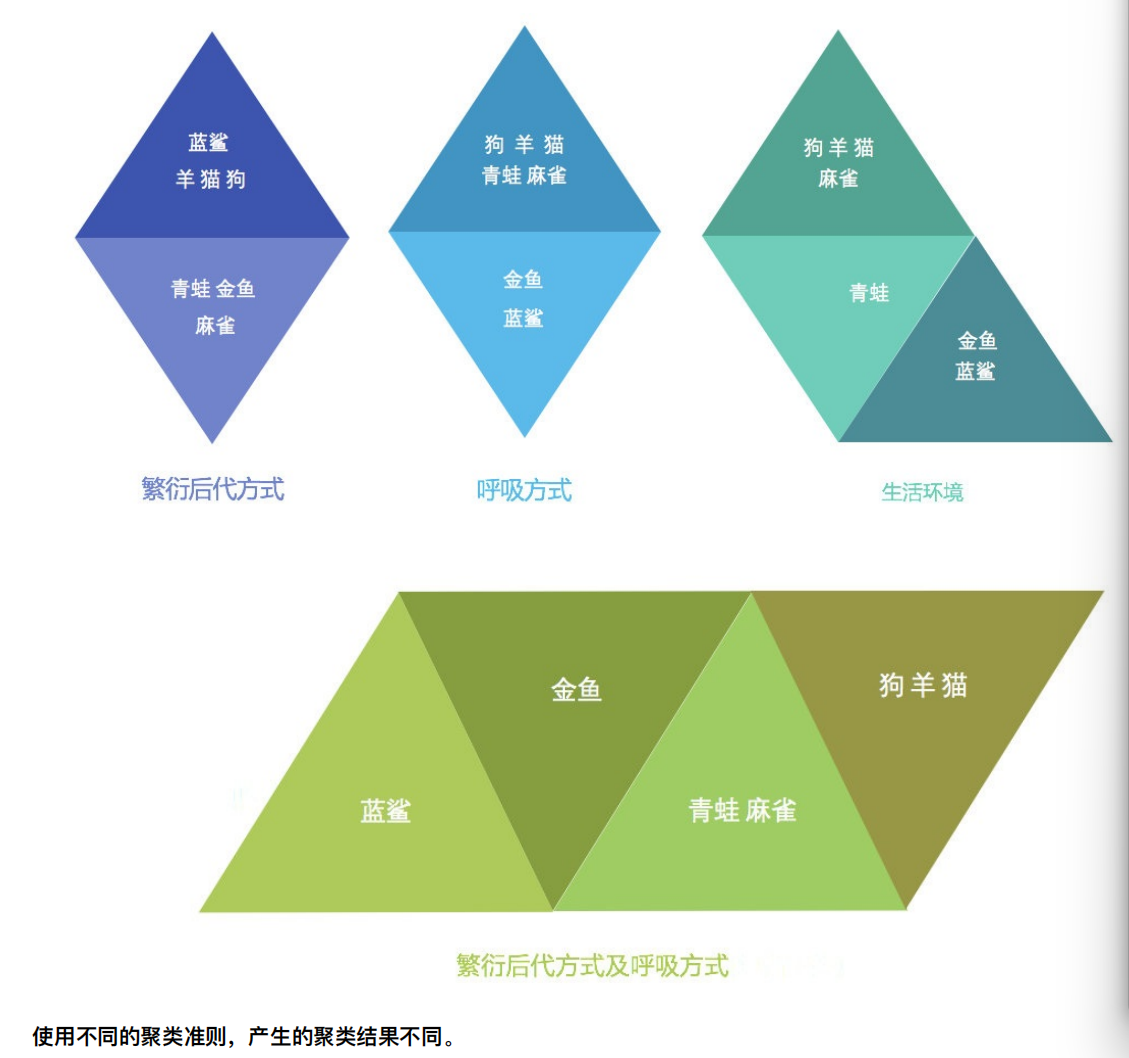
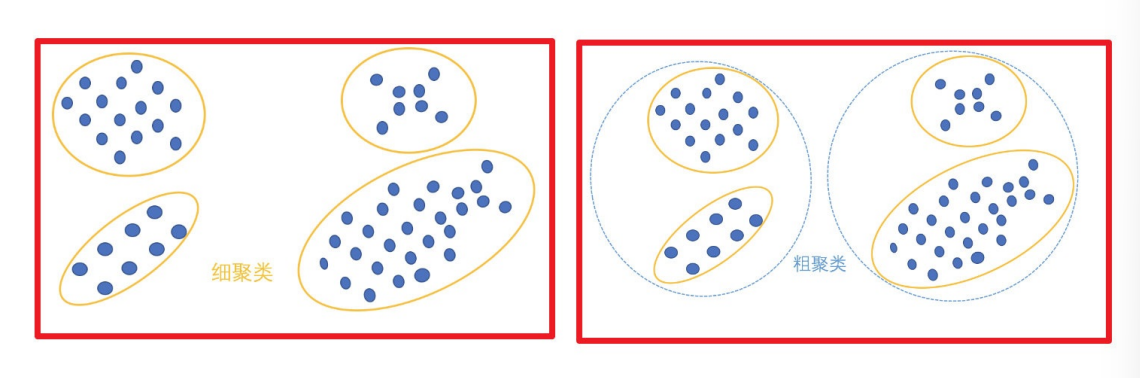
聚类算法：
⼀种典型的⽆监督学习算法，主要⽤于将相似的样本⾃动归到⼀个类别中。
在聚类算法中根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算⽅法，会得到不同的聚类结
果，常⽤的相似度计算⽅法有欧式距离法。

聚类算法是⽆监督的学习算法，⽽分类算法属于监督的学习算法。

无监督学习（Unsupervised Learning）是机器学习的一种重要范式，指的是在没有标签（label）或目标值的情况下，让模型从数据中自主发现隐藏的模式、结构或规律。

2. 聚类算法api初步使⽤

sklearn.cluster.KMeans(n_clusters=8)参数:n_clusters:开始的聚类中⼼数量整型，缺省值=8，⽣成的聚类数，即产⽣的质⼼（centroids）数。
⽅法:estimator.fit(x)estimator.predict(x)estimator.fit_predict(x)计算聚类中⼼并预测每个样本属于哪个类别,相当于先调⽤fit(x),然后再调⽤predict(x)

n_clusters意思就是有几个类
因为没有目标值，所以可以直接fit_predict

import matplotlib.pyplot as plt
#生成数据
from sklearn.datasets import make_blobs
#聚类
from sklearn.cluster import KMeans
#评价分类
from sklearn.metrics import calinski_harabasz_score

#创建数据
#创建数据
X, y = make_blobs(n_samples=1000, centers=[[-1,-1],[0,0],[1, 1], [2, 2]], n_features=2,cluster_std=[0.4, 0.3, 0.2, 0.1])

n_samples表示生成的数据个数
n_features表示特征值的个数，为2的话，表示有两个特征值，那么就是二维的了，x和y轴
centers表示生成的数据的中心点
cluster_std表示中心点数据的标准差–》也就是密集程度

X：生成的样本数据，形状为 (1000, 2) 的数组
y：每个样本的真实聚类标签，取值为 0、1、2、3（对应 4 个聚类中心）

plt.scatter(X[:,0], X[:,1], marker='o')
plt.show()

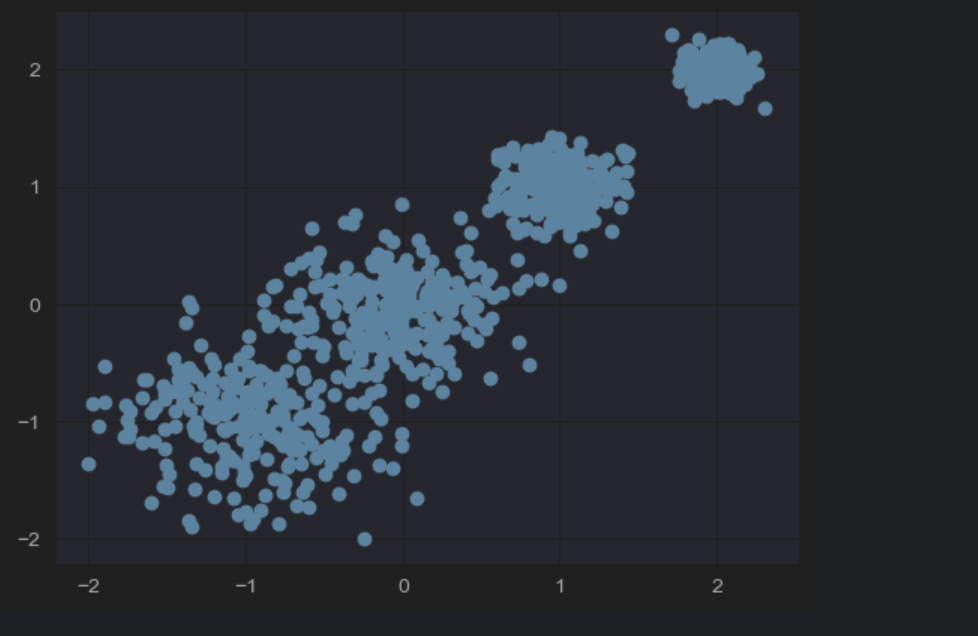
#kmeans训练
y_pre = KMeans(n_clusters=2, random_state=0).fit_predict(X)
#可视化展示
plt.scatter(X[:,0], X[:,1],c=y_pre, marker='o')
plt.show()
#查看最后效果
print(calinski_harabasz_score(X, y_pre))

n_clusters表示分为两类
fit_predict(X)
功能：对输入数据 X 进行拟合（训练 K-Means 模型），并直接返回每个样本的聚类标签。
c=y_pre
含义：根据聚类标签 y_pre 为散点着色，同一聚类的样本会显示相同颜色，不同聚类颜色不同。
y_pre是和X一一对应的

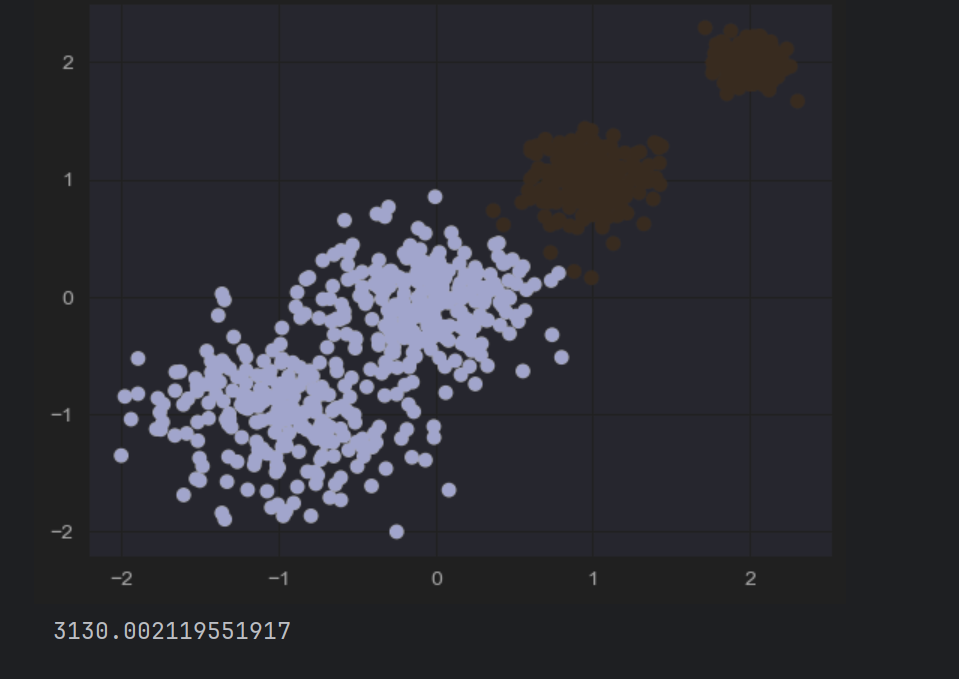
三千多表示的是聚类效果，值越大越好

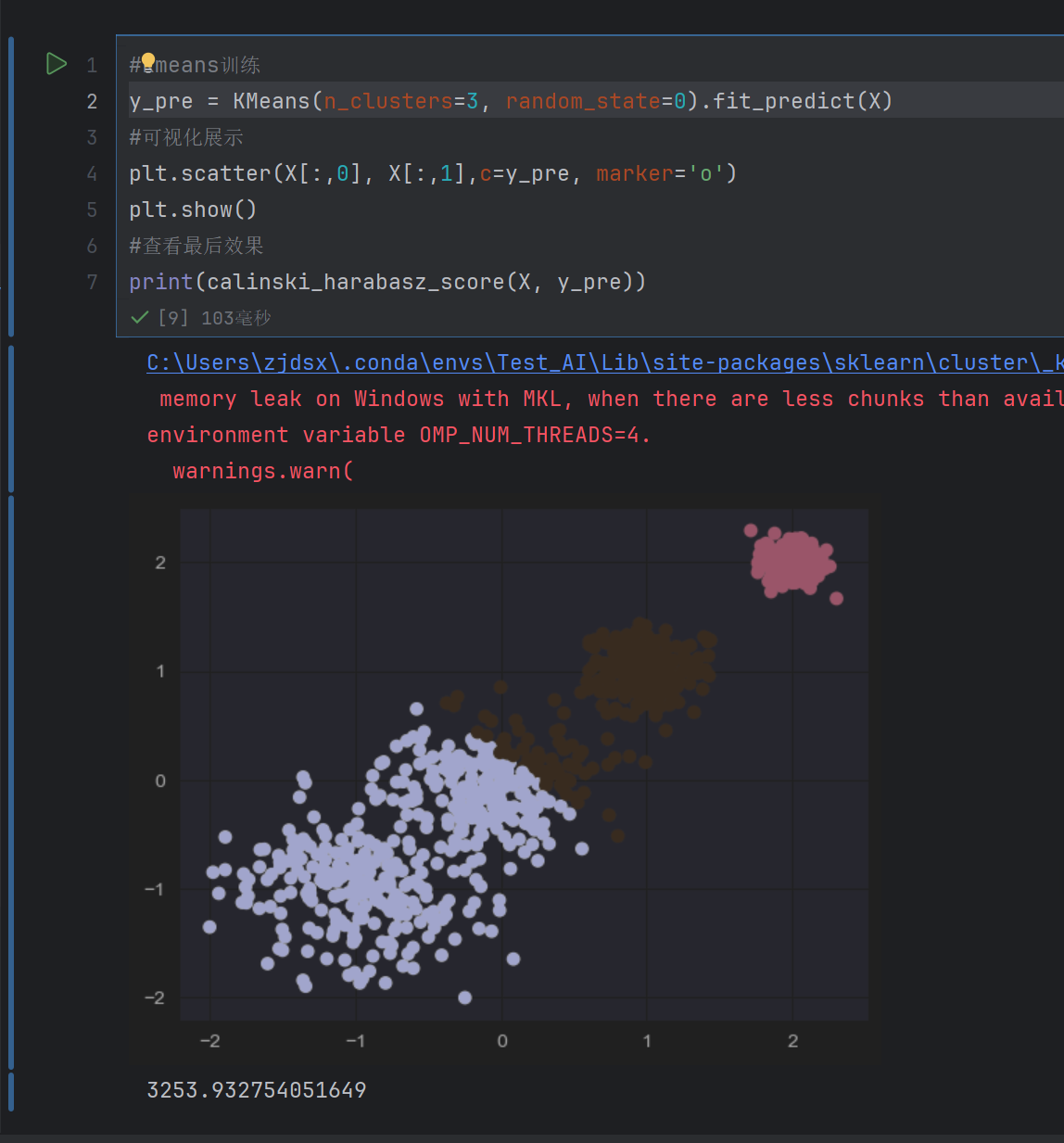
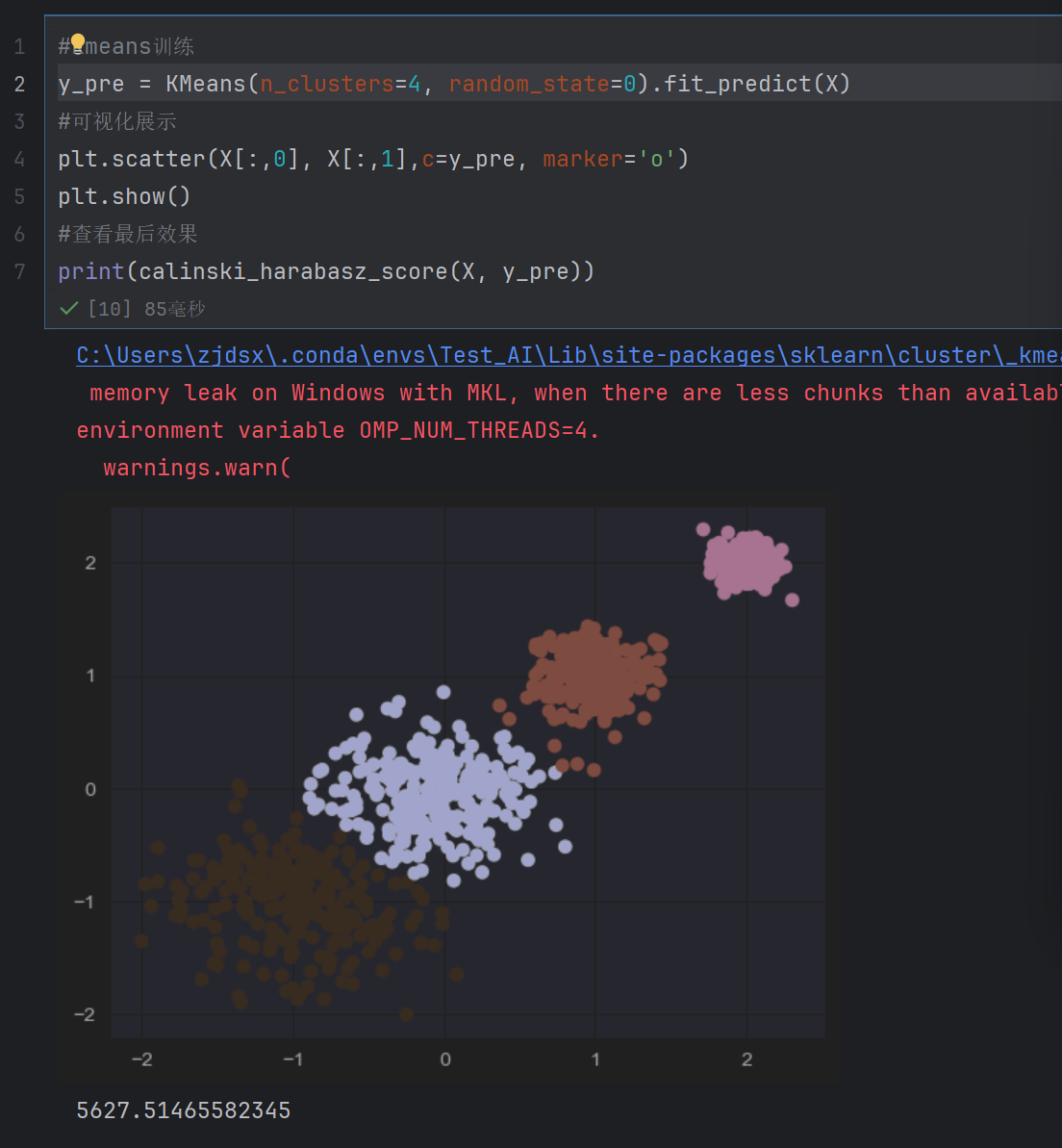
发现四个的时候最好

3. 聚类算法实现流程

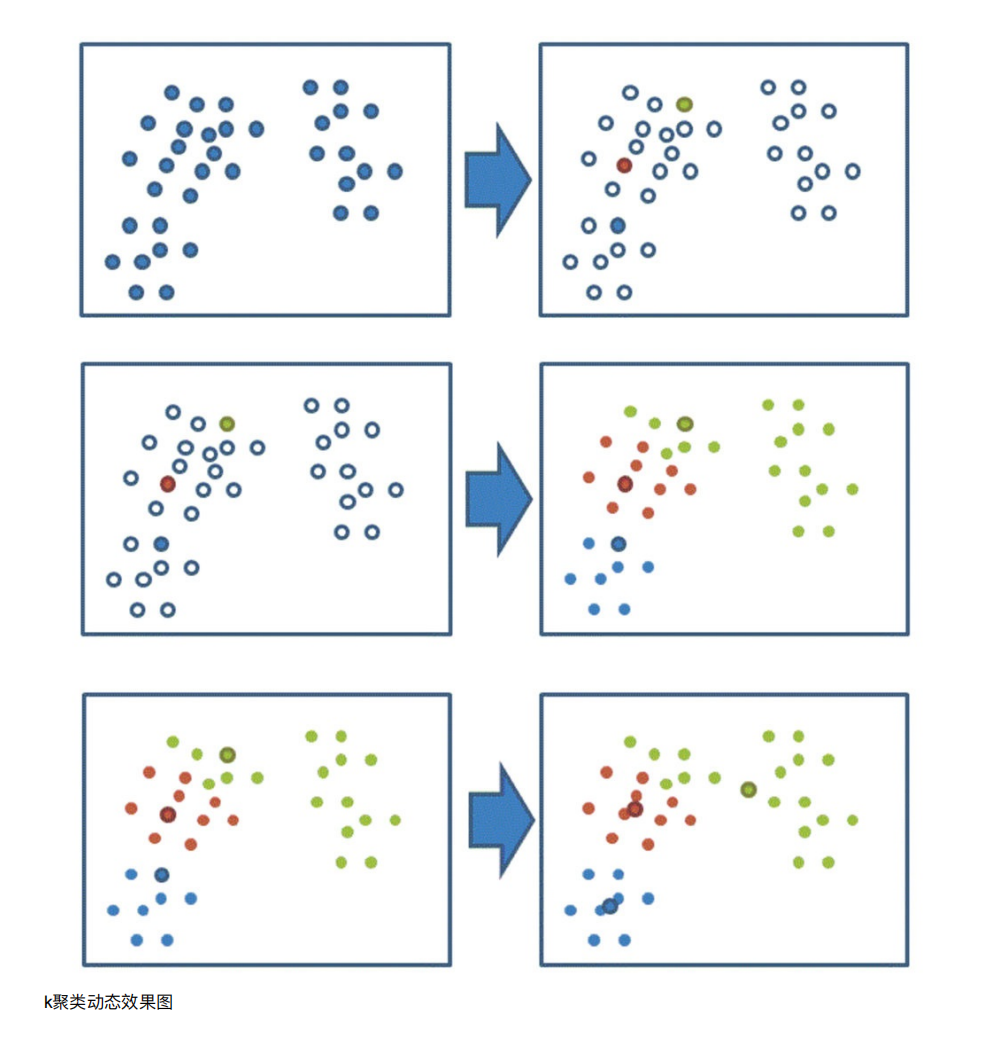
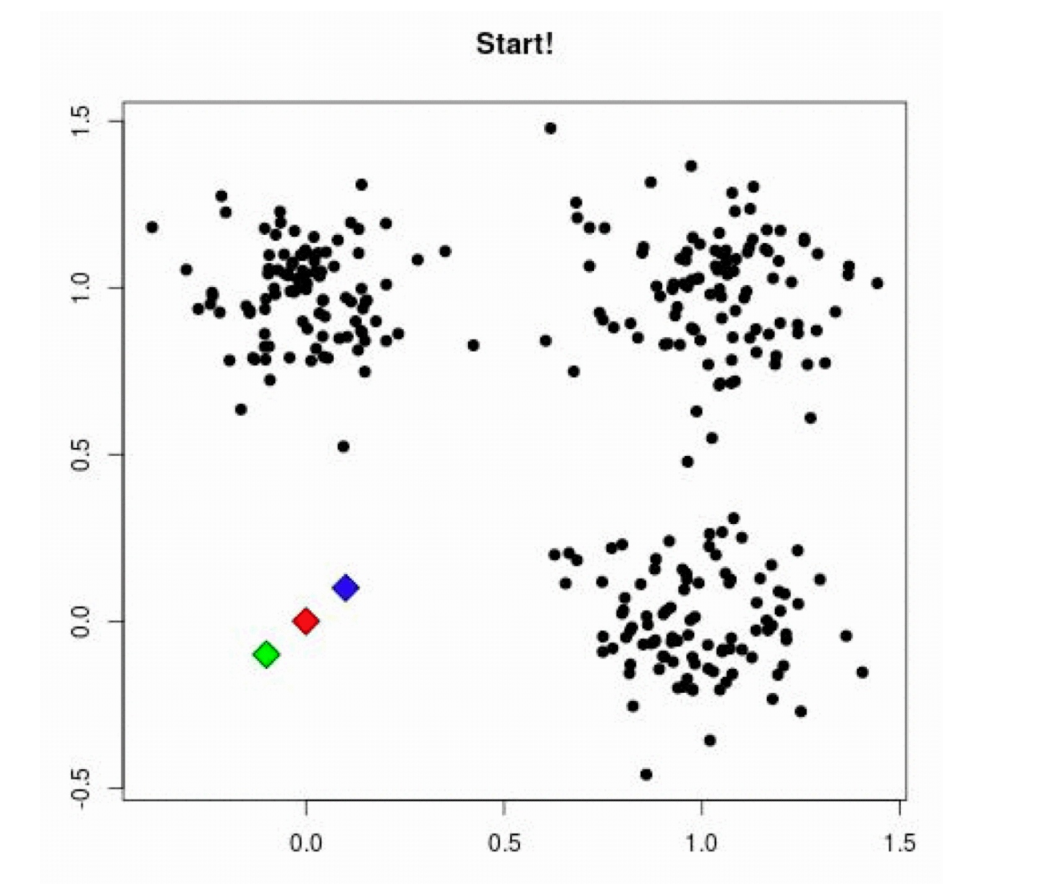
案例练习

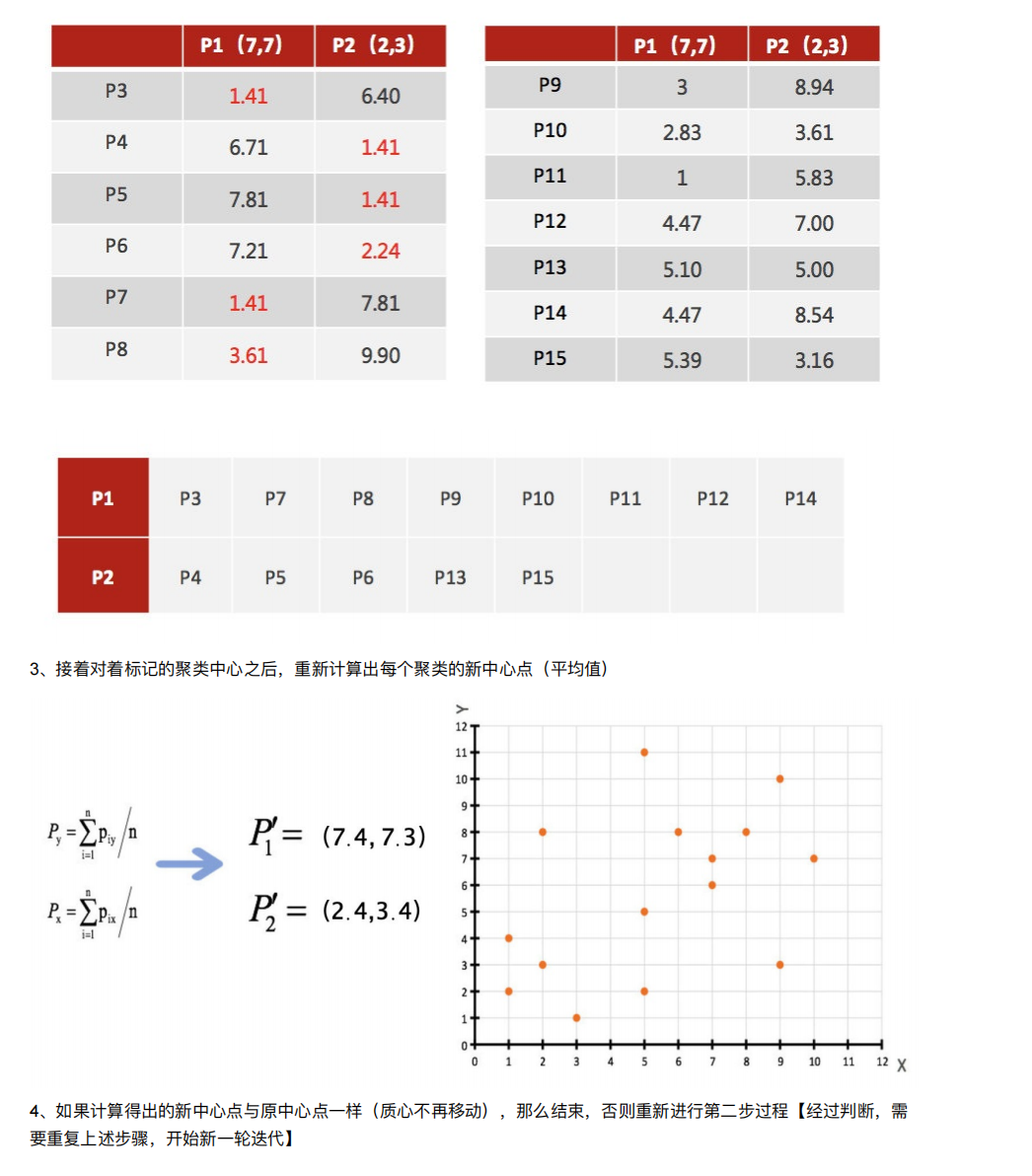
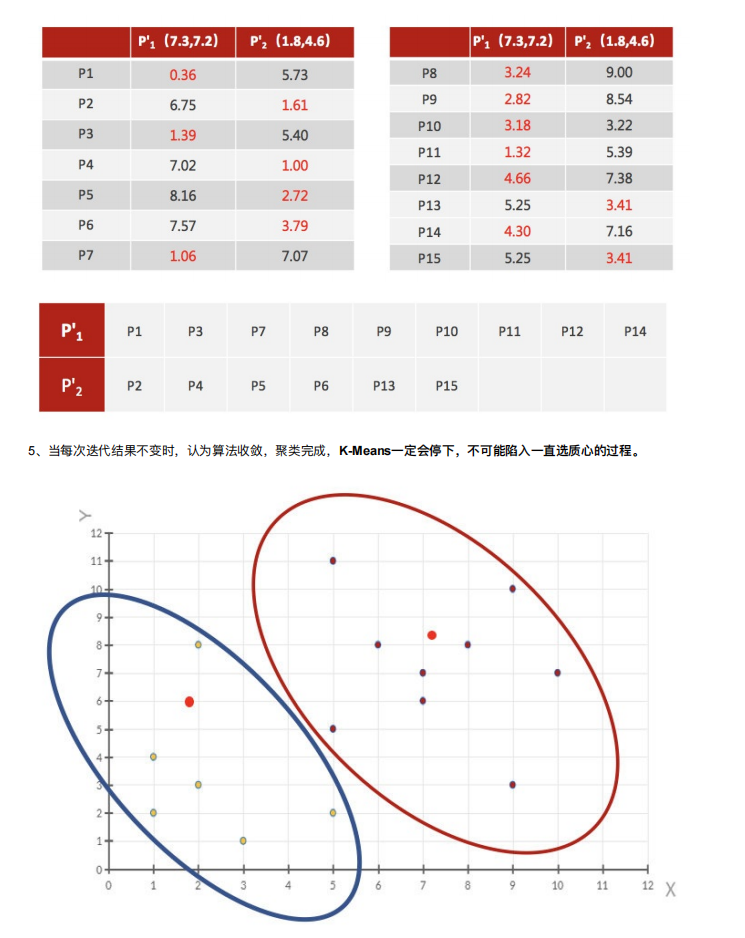
4. 模型评估

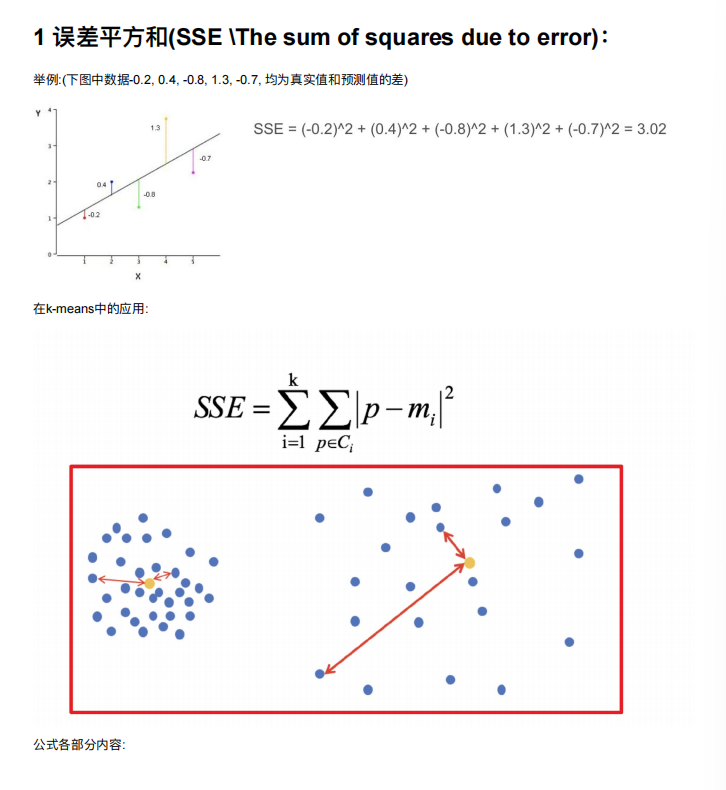
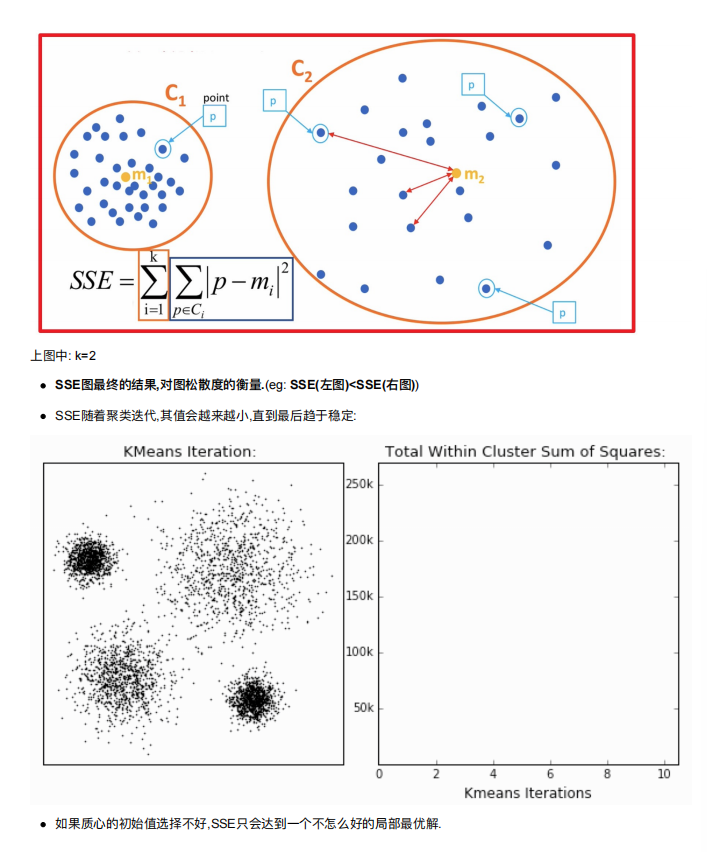
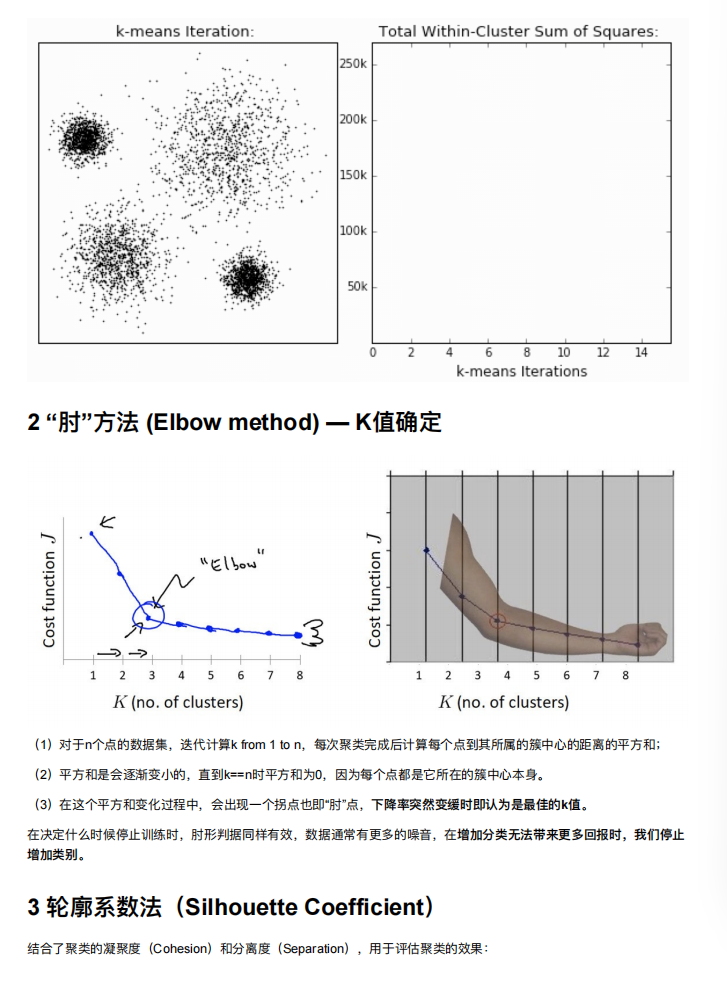
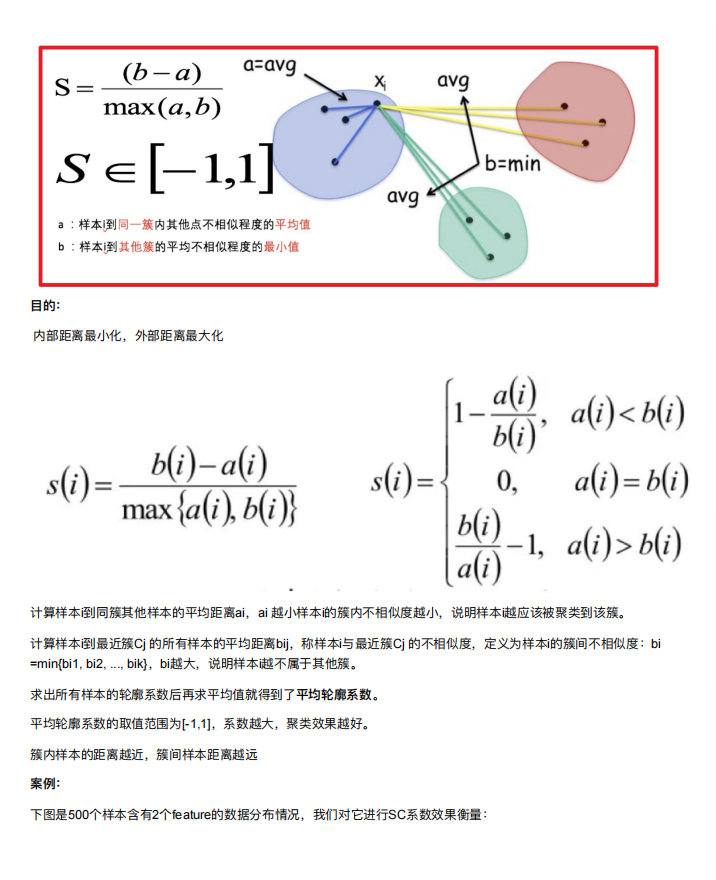
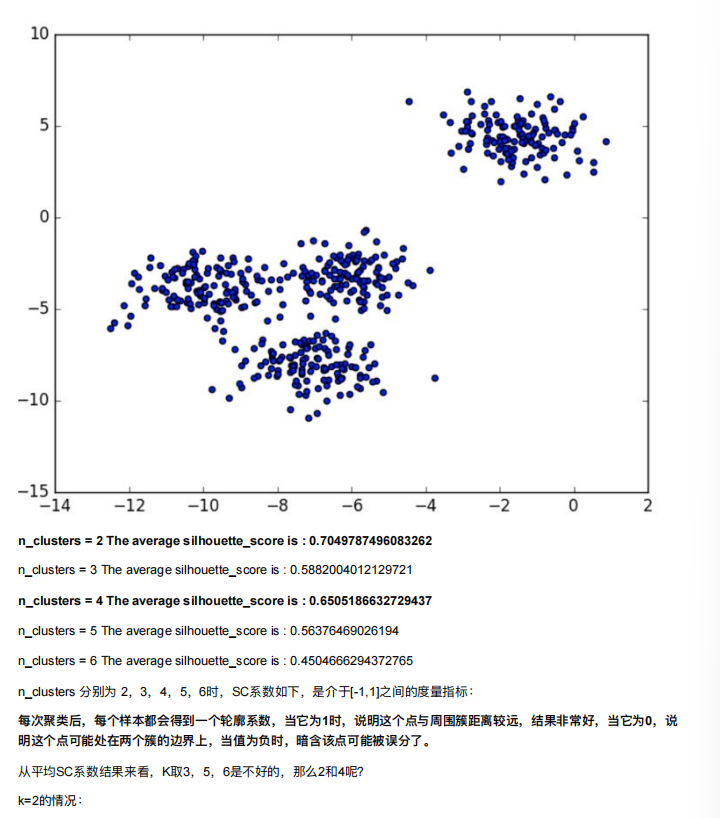
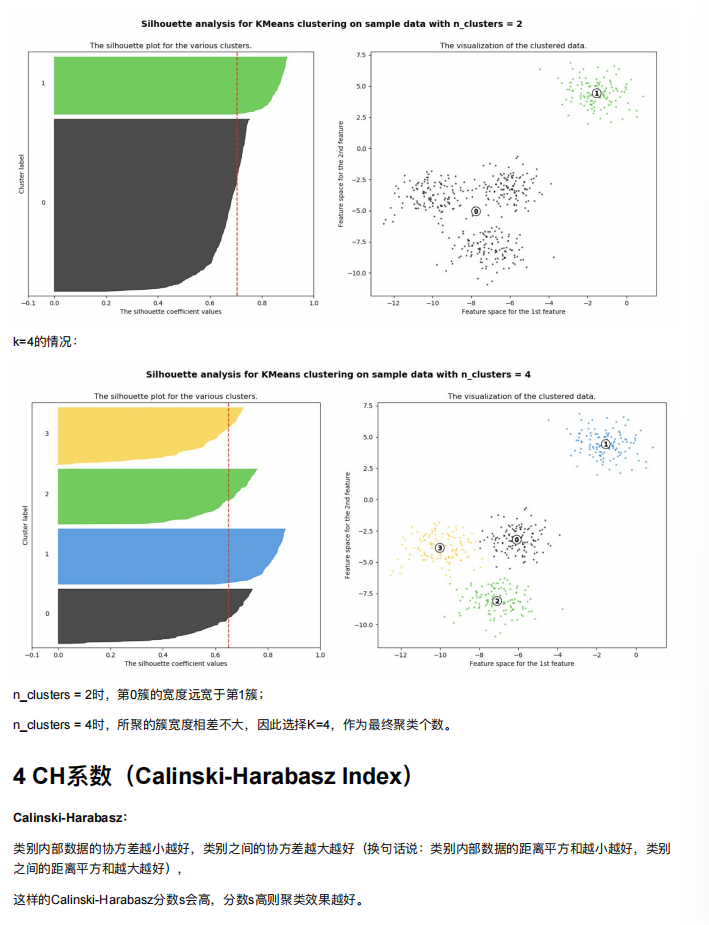
5. 算法优化

5.1 Canopy算法配合初始聚类

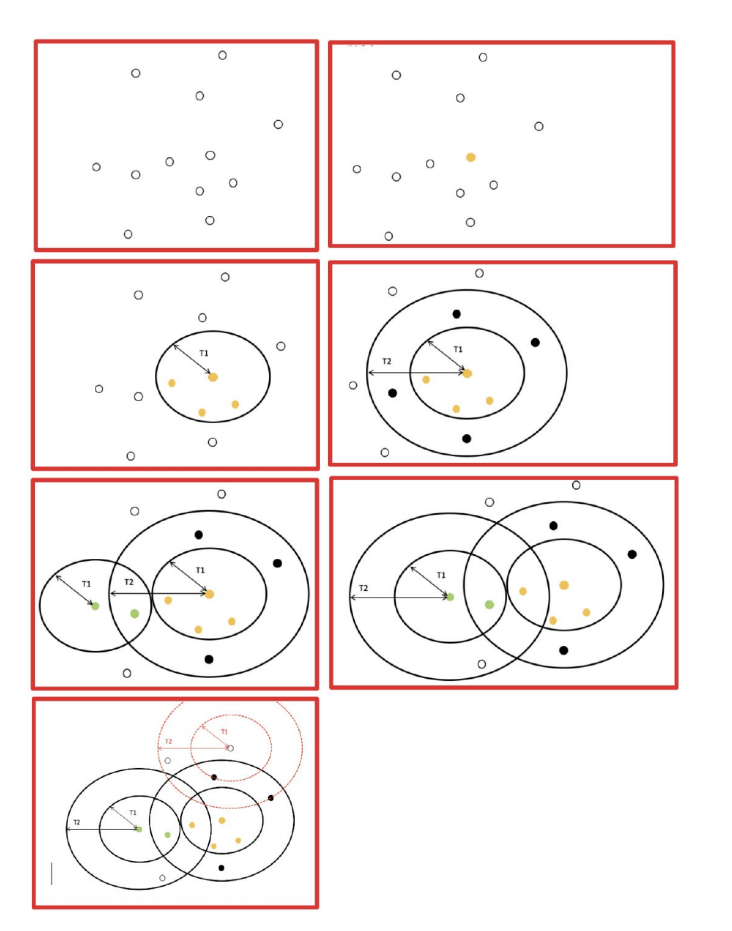
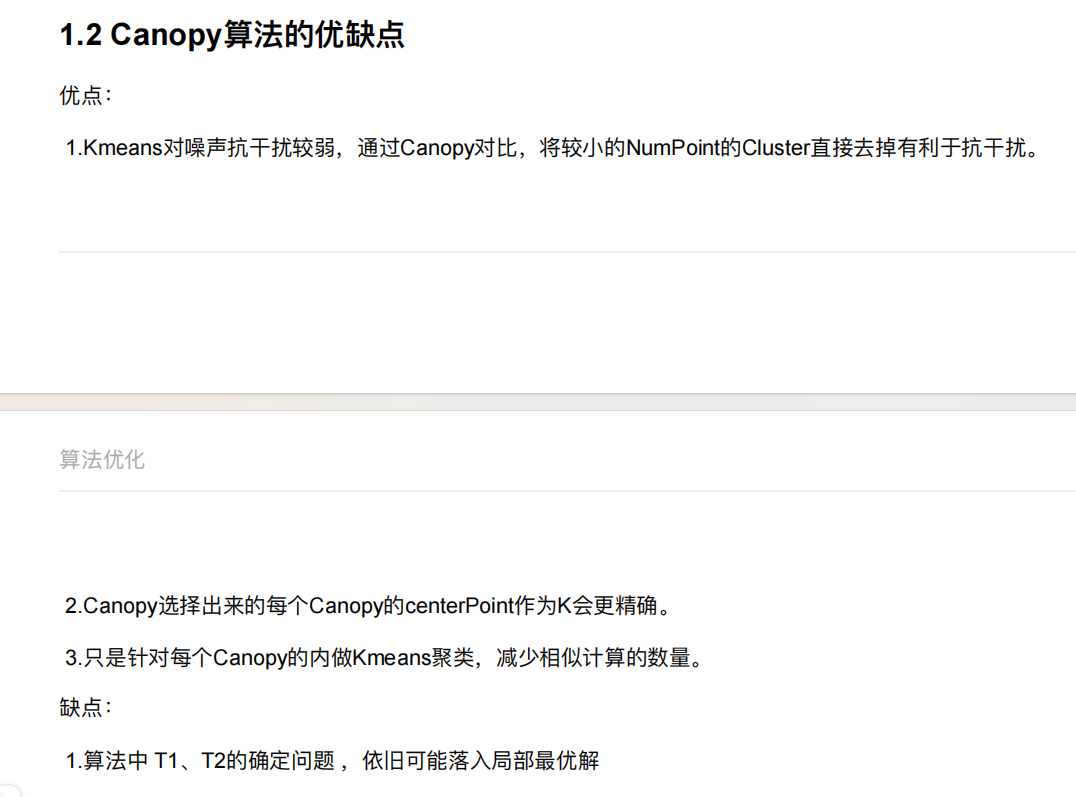
5.2 K-means++

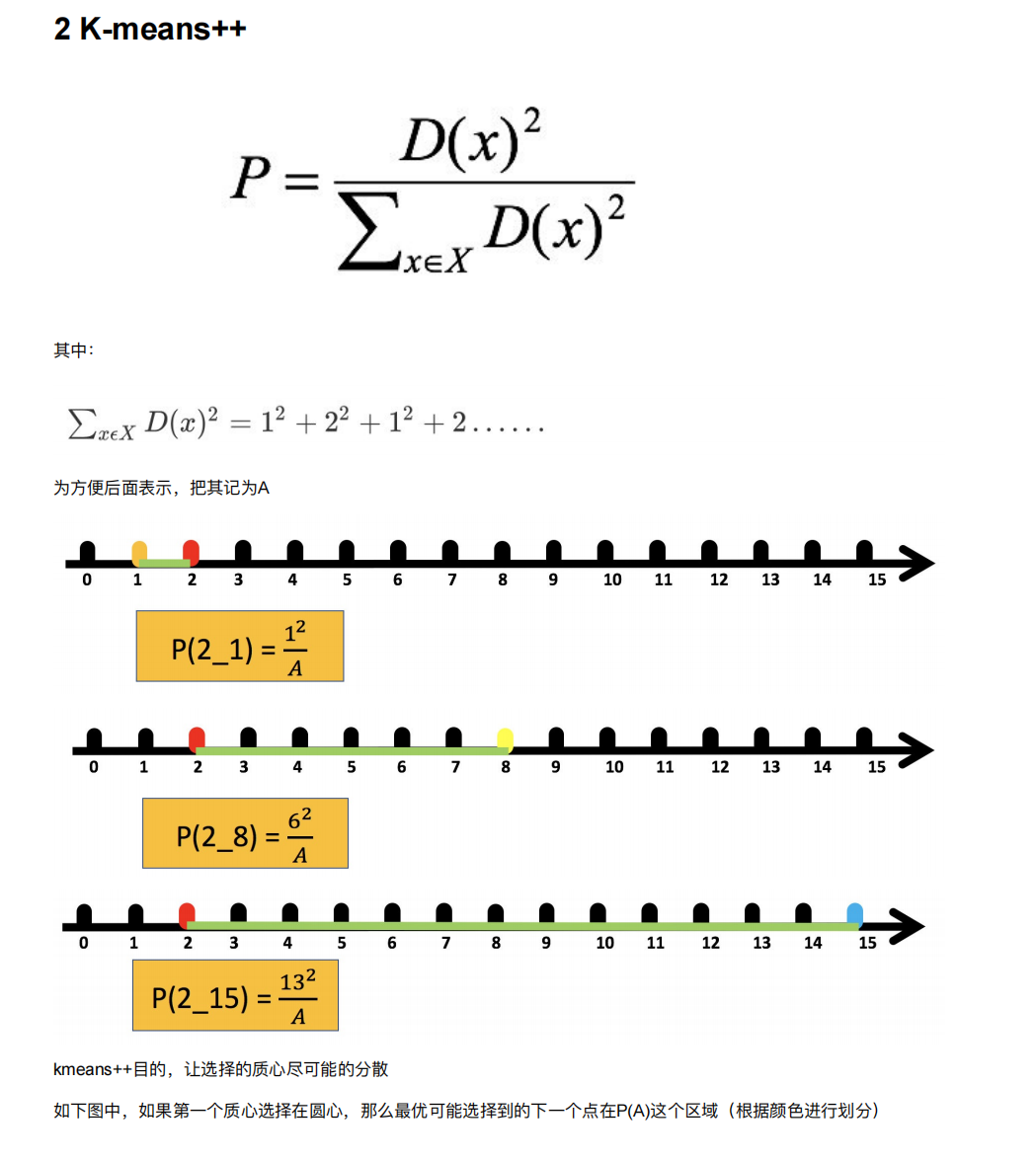
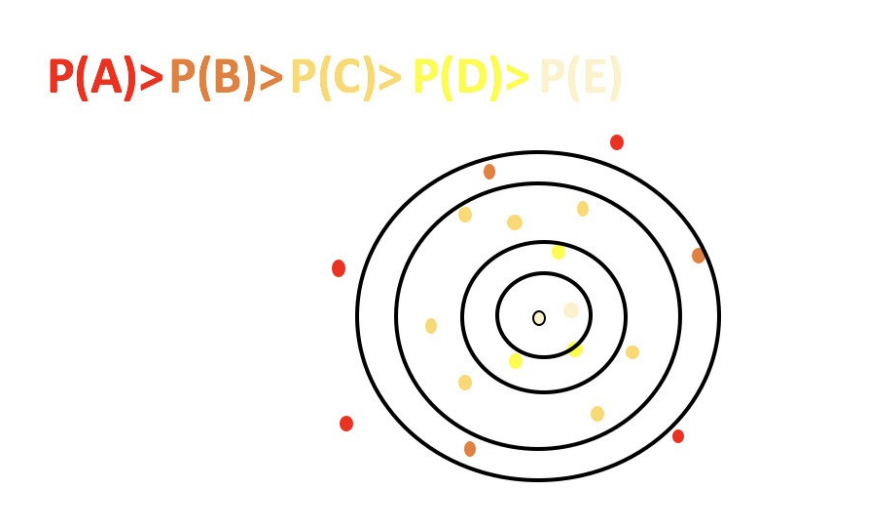
5.3 ⼆分k-means

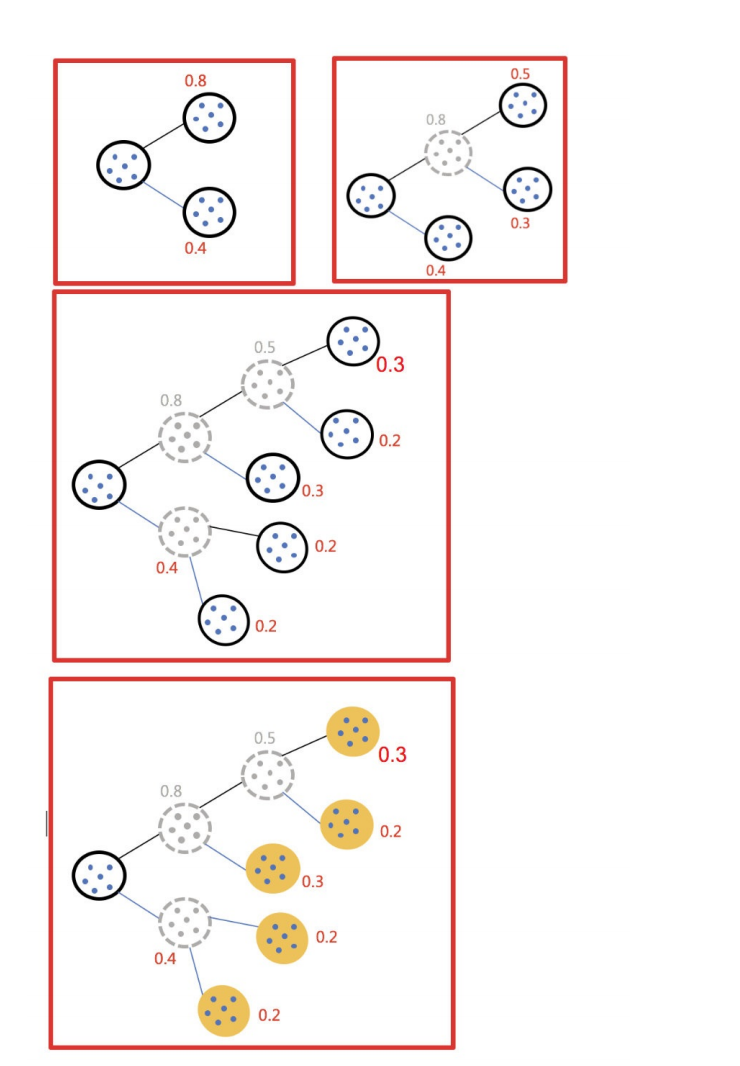
5.4 k-medoids（k-中⼼聚类算法）

5.5 了解

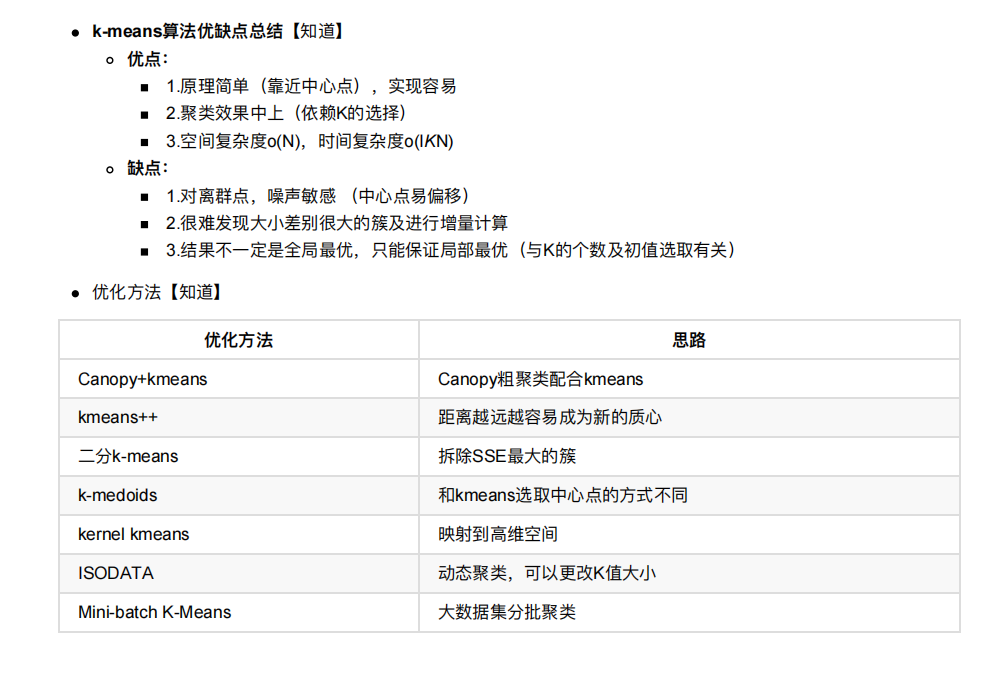
6. 特征降维

降维是指在某些限定条件下，降低随机变量(特征)个数，得到⼀组“不相关”主变量的过程

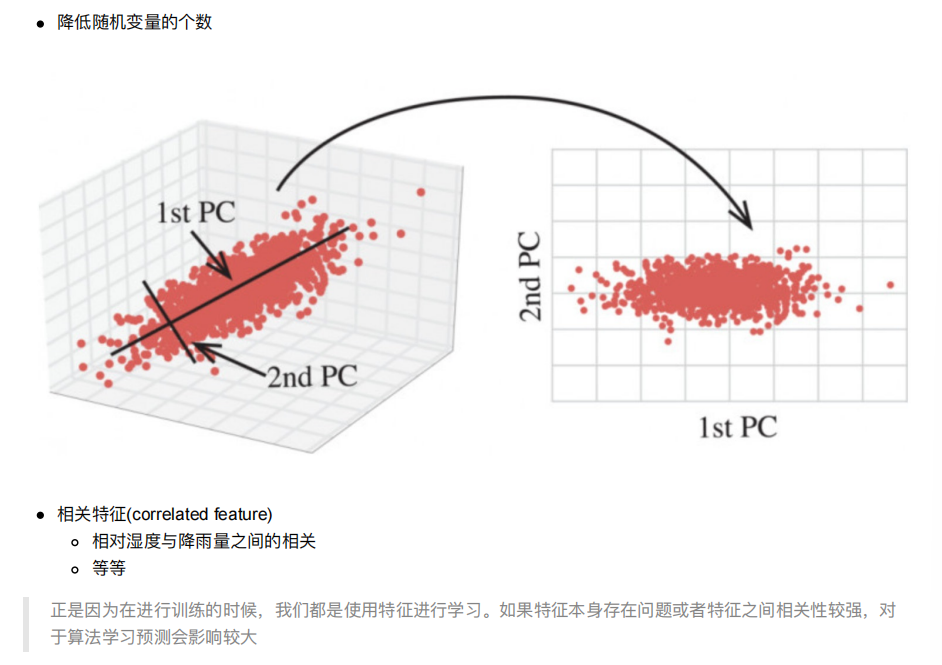
降维的两种⽅式
特征选择
主成分分析（可以理解⼀种特征提取的⽅式）

6.1 特征选择

⽅法
Filter(过滤式)：主要探究特征本身特点、特征与特征和⽬标值之间关联⽅差选择法：低⽅差特征过滤相关系数
Embedded (嵌⼊式)：算法⾃动选择特征（特征与⽬标值之间的关联）决策树:信息熵、信息增益正则化：L1、L2深度学习：卷积等

低⽅差特征过滤
删除低⽅差的⼀些特征，前⾯讲过⽅差的意义。再结合⽅差的⼤⼩来考虑这个⽅式的⻆度。
特征⽅差⼩：某个特征⼤多样本的值⽐较相近—》无关
特征⽅差⼤：某个特征很多样本的值都有差别

API
sklearn.feature_selection.VarianceThreshold(threshold = 0.0)删除所有低⽅差特征Variance.fit_transform(X)X:numpy array格式的数据[n_samples,n_features]返回值：训练集差异低于threshold的特征将被删除。默认值是保留所有⾮零⽅差特征，即删除所有样本中具有相同值的特征。

threshold 就是那个方差临界值，小于threshold 方差的都去掉

我们对某些股票的指标特征之间进⾏⼀个筛选，除去’index,‘date’,'return’列不考虑（这些类型不匹配，也不是所需要指
标）

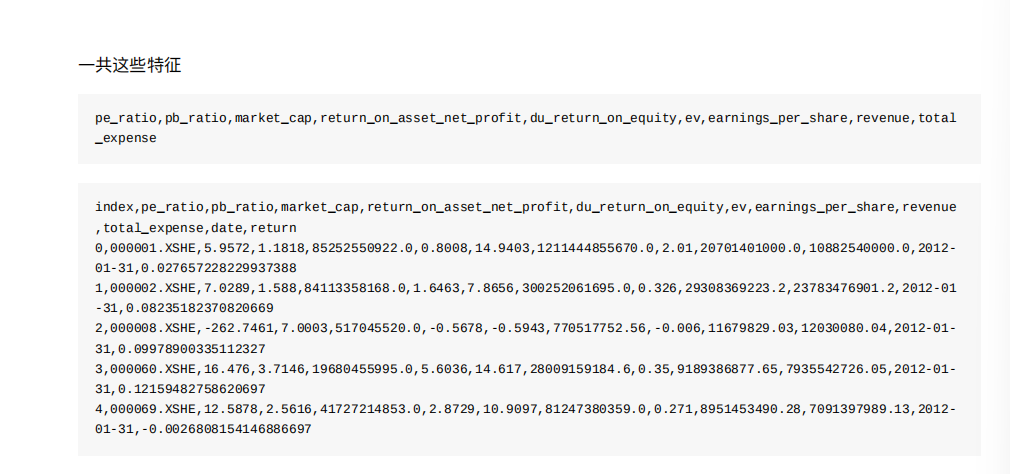
import  pandas as pd
# 特征选择
from sklearn.feature_selection import VarianceThreshold
def var_thr():#特征选择data=pd.read_csv("./data/factor_returns.csv")transfer=VarianceThreshold(threshold=1)#转化,data.iloc[:,1:10]：是所有行，1到10列，因为索引和后面的日期。return不要ret_data=transfer.fit_transform(data.iloc[:,1:10])print("原始数据：\n",data.iloc[:,1:10].shape)print("特征选择后的数据：\n",ret_data.shape)if __name__ == '__main__':var_thr()

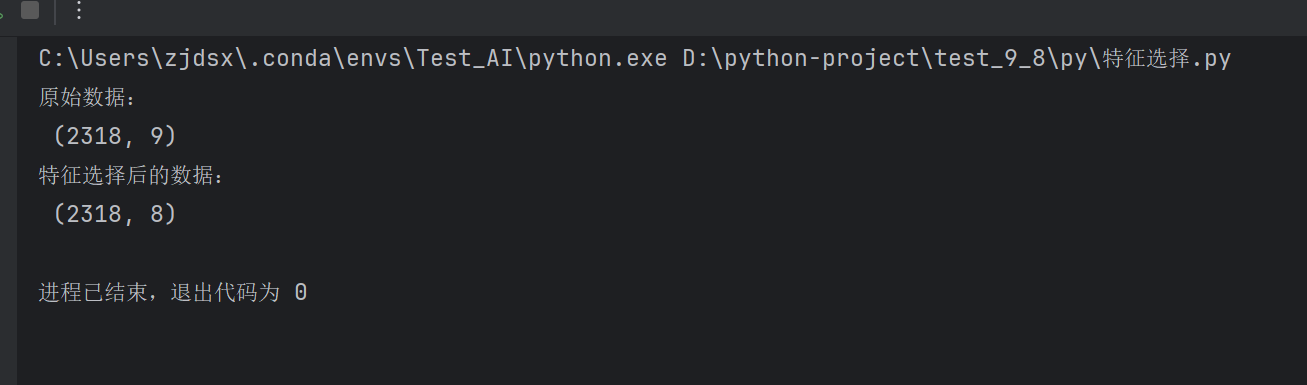
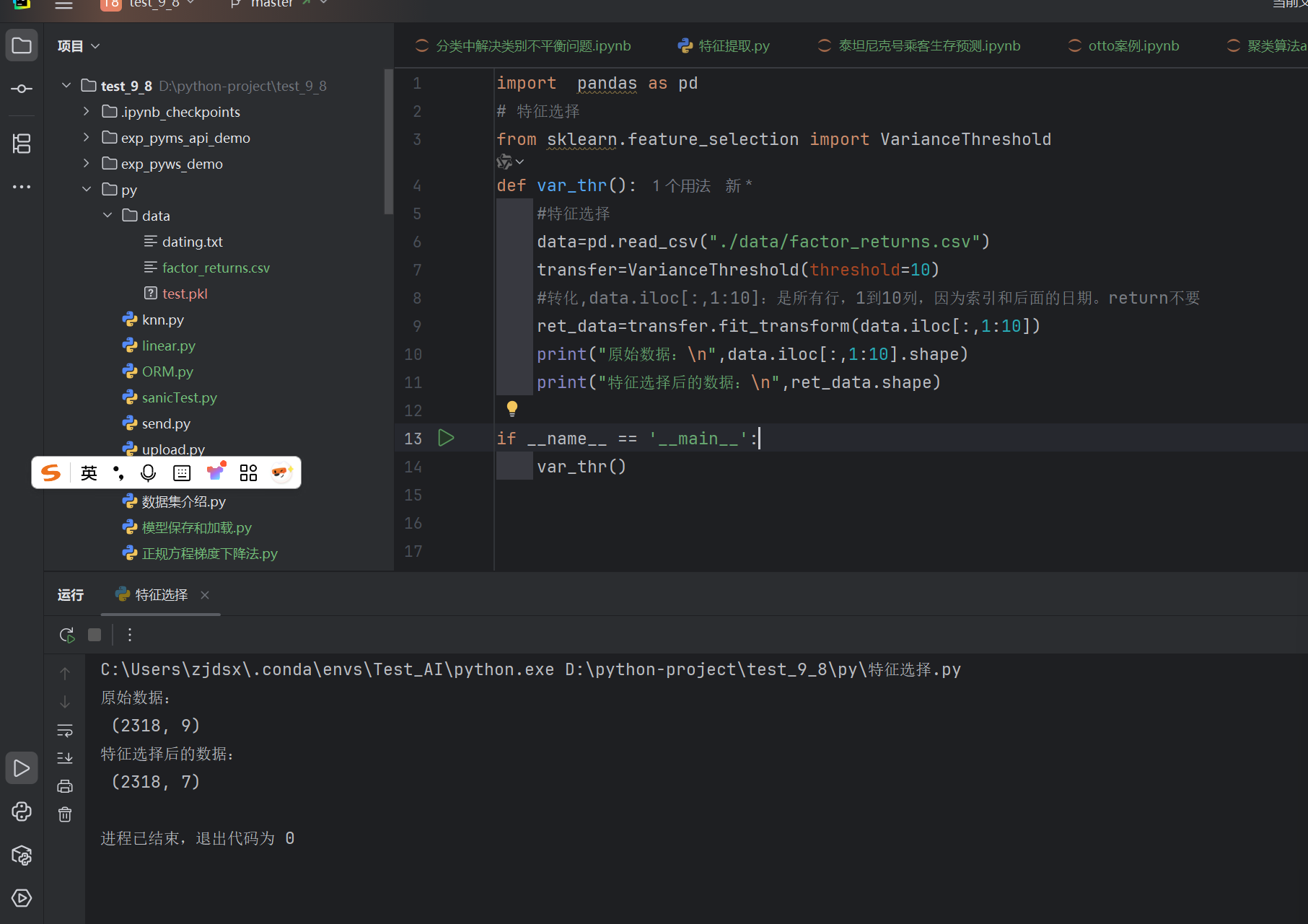
发现方差小的都删除了

相关系数
主要实现⽅式：
⽪尔逊相关系数
斯⽪尔曼相关系数

6.2 ⽪尔逊相关系数(Pearson Correlation Coefficient)

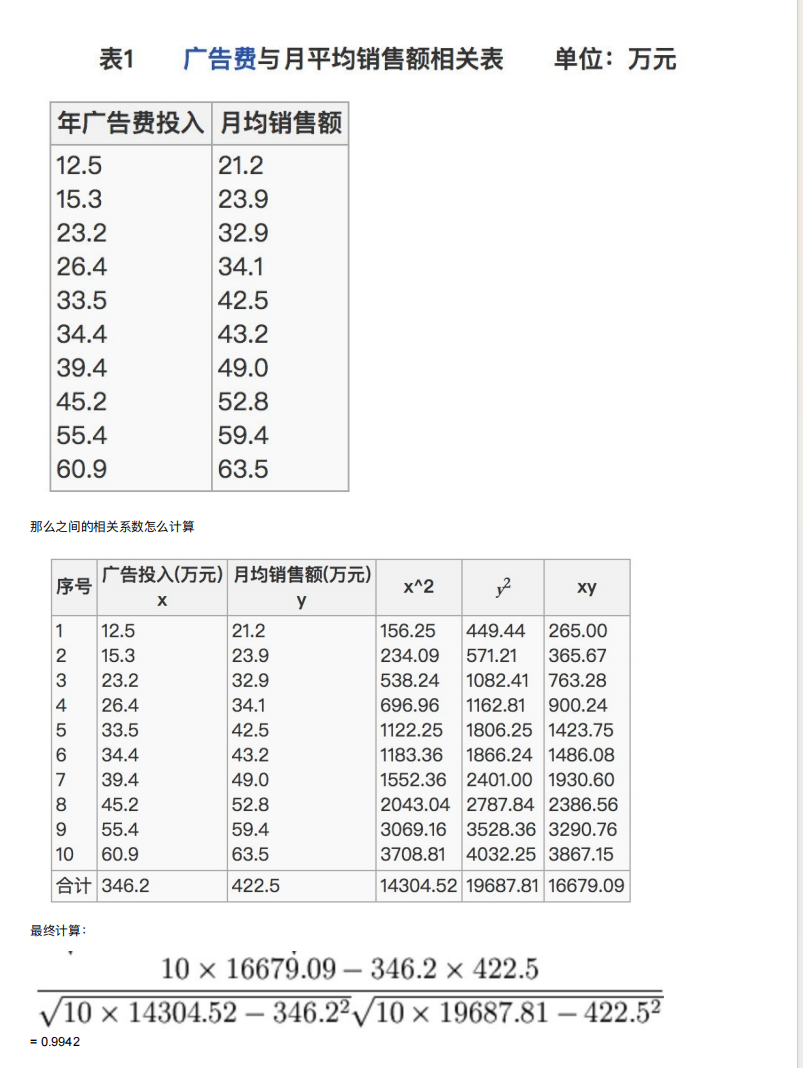
api

from scipy.stats import pearsonrx : (N,) array_likey : (N,) array_like Returns: (Pearson’s correlation coefficient, p-value)

def pea_demo():#准备数据x1 = [12.5, 15.3, 23.2, 26.4, 33.5, 34.4, 39.4, 45.2, 55.4, 60.9]x2 = [21.2, 23.9, 32.9, 34.1, 42.5, 43.2, 49.0, 52.8, 59.4, 63.5]print("皮尔逊相关系数：\n",pearsonr(x1,x2))

第一个值是0.99，说明相关性很高
第二个值是这样说的，当数量大于500的时候有参考意义，越接近于0，相关性就越高

6.3 斯⽪尔曼相关系数(Rank IC)

1.作⽤：
反映变量之间相关关系密切程度的统计指标

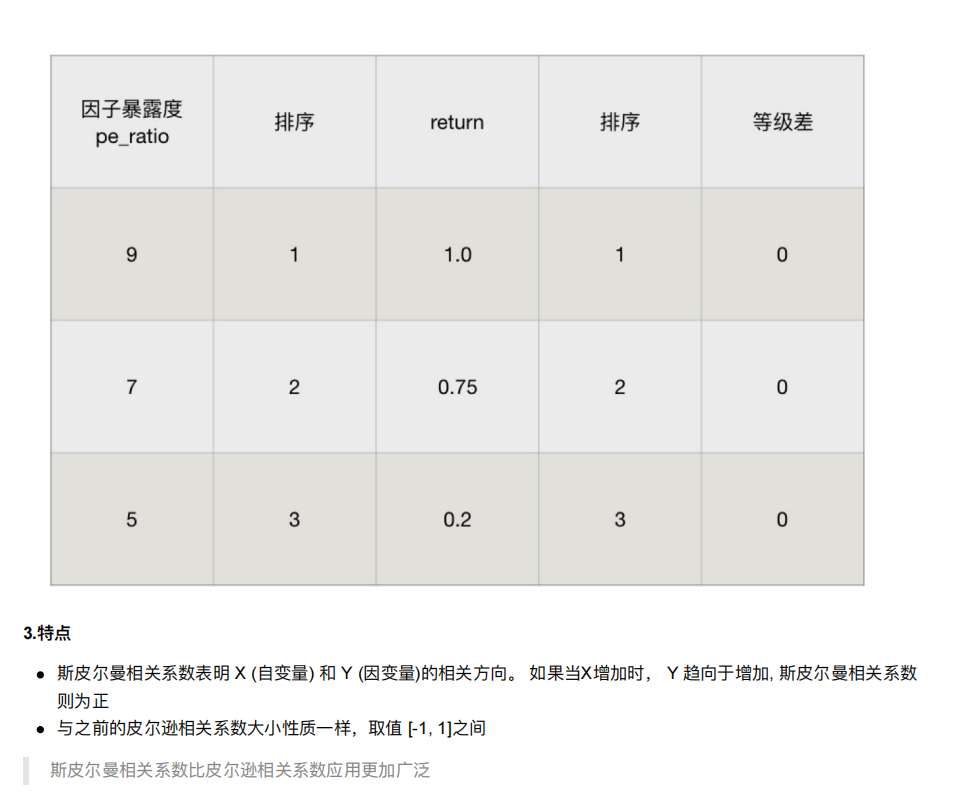
def spea_demo():# 准备数据x1 = [12.5, 15.3, 23.2, 26.4, 33.5, 34.4, 39.4, 45.2, 55.4, 60.9]x2 = [21.2, 23.9, 32.9, 34.1, 42.5, 43.2, 49.0, 52.8, 59.4, 63.5]print("斯皮尔曼相关系数：\n",spearmanr(x1,x2))

6.4 主成分分析

定义：⾼维数据转化为低维数据的过程，在此过程中可能会舍弃原有数据、创造新的变量
作⽤：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。
应⽤：回归分析或者聚类分析当中

就是特征值的合并

sklearn.decomposition.PCA(n_components=None)将数据分解为较低维数空间n_components:⼩数：表示保留百分之多少的信息整数：减少到多少特征PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features]返回值：转换后指定维度的array

from sklearn.decomposition import PCA
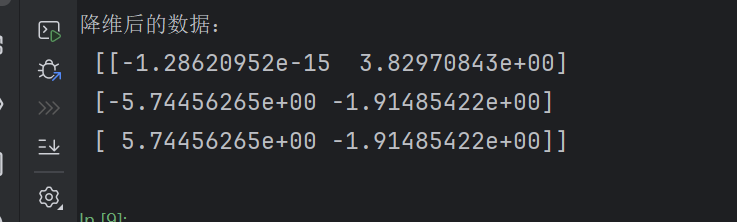
def pca_demo():# PCAdata = [[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]]#小数保留百分比，表示保留90%的信息pca = PCA(n_components=0.9)ret_data = pca.fit_transform(data)print("降维后的数据：\n",ret_data)

原始数据是 3 个样本，每个样本有 4 个特征（4 列）
当设置n_components=0.9时，PCA 计算发现只需要2 个主成分就能保留超过 90% 的原始信息
因此降维后的数据变成了 2 列（每个主成分对应一列）

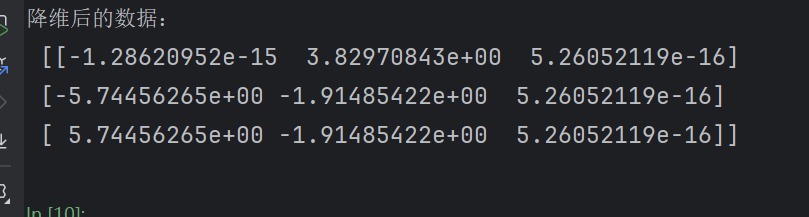
    #表示保留三列数据pca = PCA(n_components=3)ret_data = pca.fit_transform(data)print("降维后的数据：\n",ret_data)

7. 案例：探究⽤户对物品类别的喜好细分

应⽤pca和K-means实现⽤户对物品类别的喜好细分划分

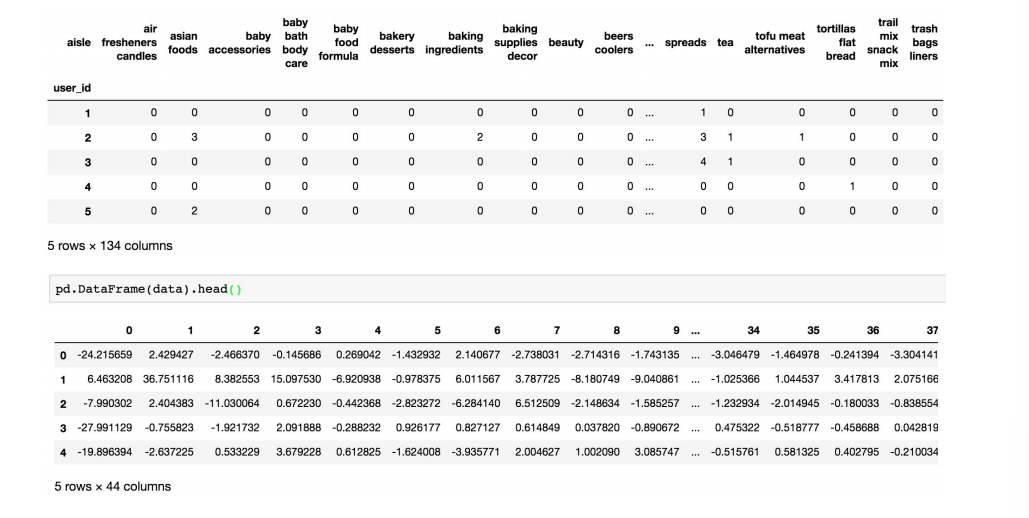
多个表需要合并，因为两两都有相同的字段

import pandas as pd
order_product = pd.read_csv('./source/instacart/order_products__prior.csv')
products = pd.read_csv('./source/instacart/products.csv')
orders   = pd.read_csv('./source/instacart/orders.csv')
aisles   = pd.read_csv('./source/instacart/aisles.csv')

import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score

# 2.数据基本处理
# 2.1 合并表格
table1 = pd.merge(order_product, products, on=["product_id","product_id"])

table2 = pd.merge(table1, orders, on=["order_id","order_id"])
table = pd.merge(table2, aisles, on=["aisle_id","aisle_id"])

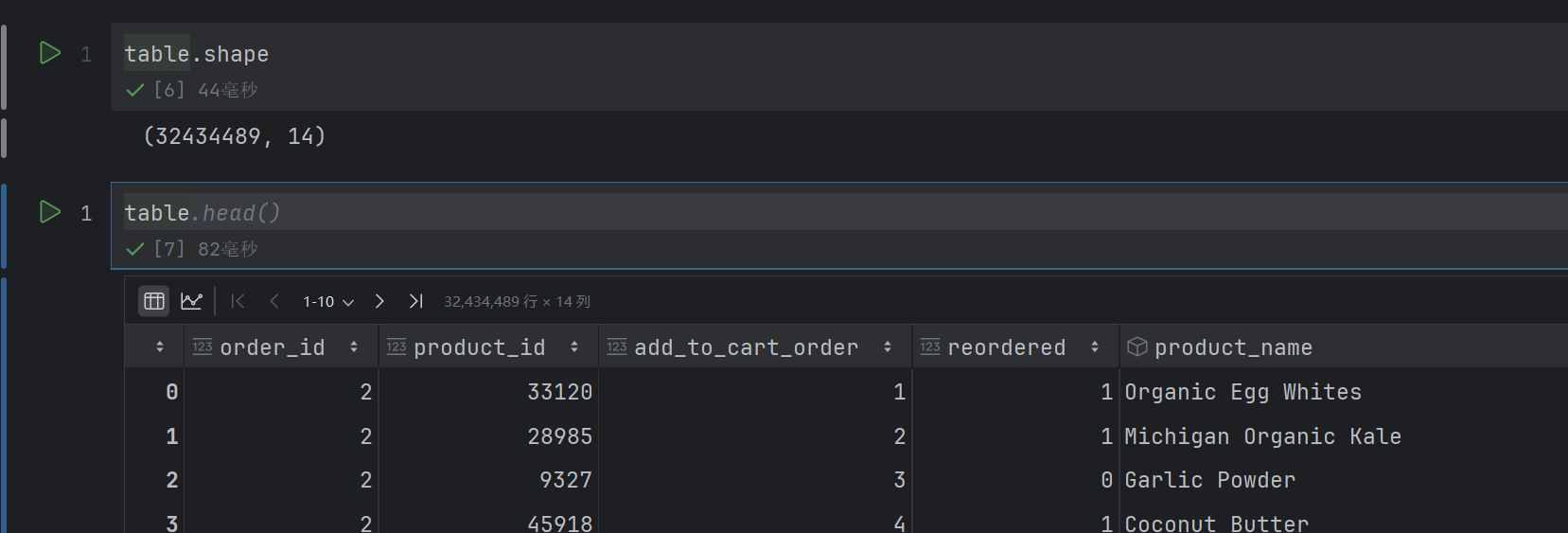
# 2.2 交叉表合并
data = pd.crosstab(table["order_id"], table["aisle"])

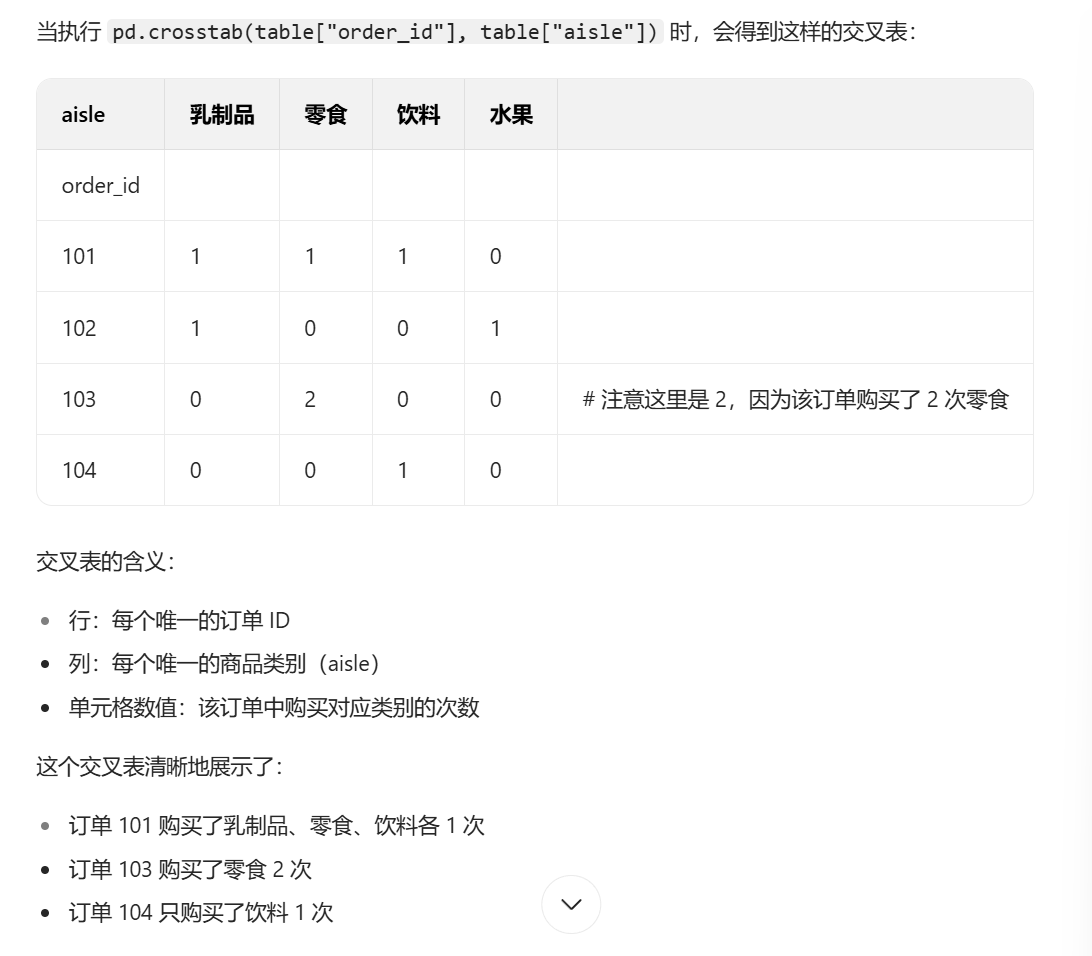
反正意思就是以order_id作为行索引，aisle作为列索引。求出每个order_id中每个aisle的数量

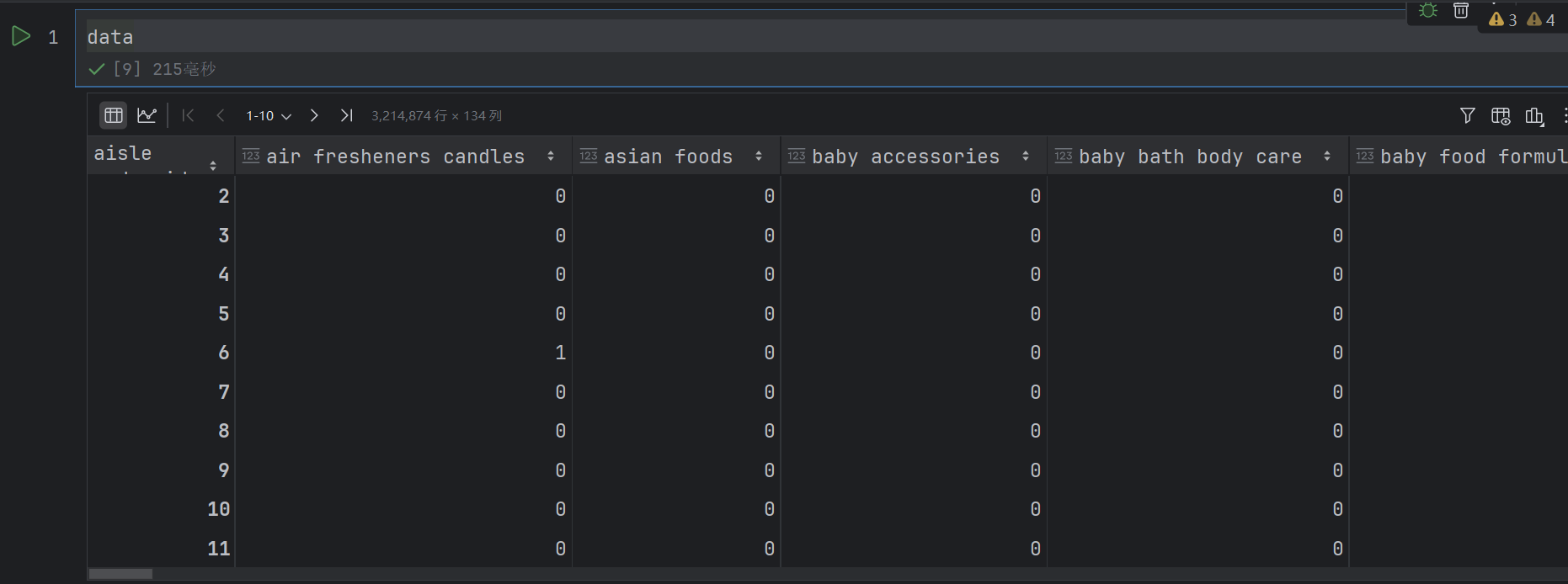
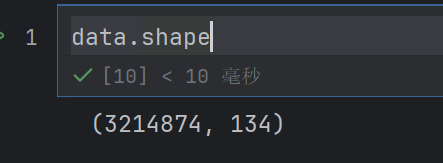
# 2.3 数据截取
new_data = data[:1000]

# 3.特征⼯程 — pca
transfer = PCA(n_components=0.9)
trans_data = transfer.fit_transform(new_data)

发现只有48个特征了

# 4.机器学习（k-means）
estimator = KMeans(n_clusters=5)
y_pre=estimator.fit_predict(trans_data)

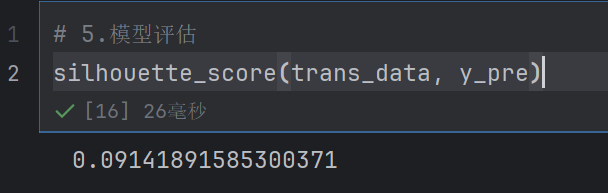
接近1效果就越好，但是我们这个不好

总结