当前位置：首页 > news >正文

语义精炼技巧生成对抗网络（3）基于Wasserstein GAN 的特征生成

news 2025/9/24 12:44:48

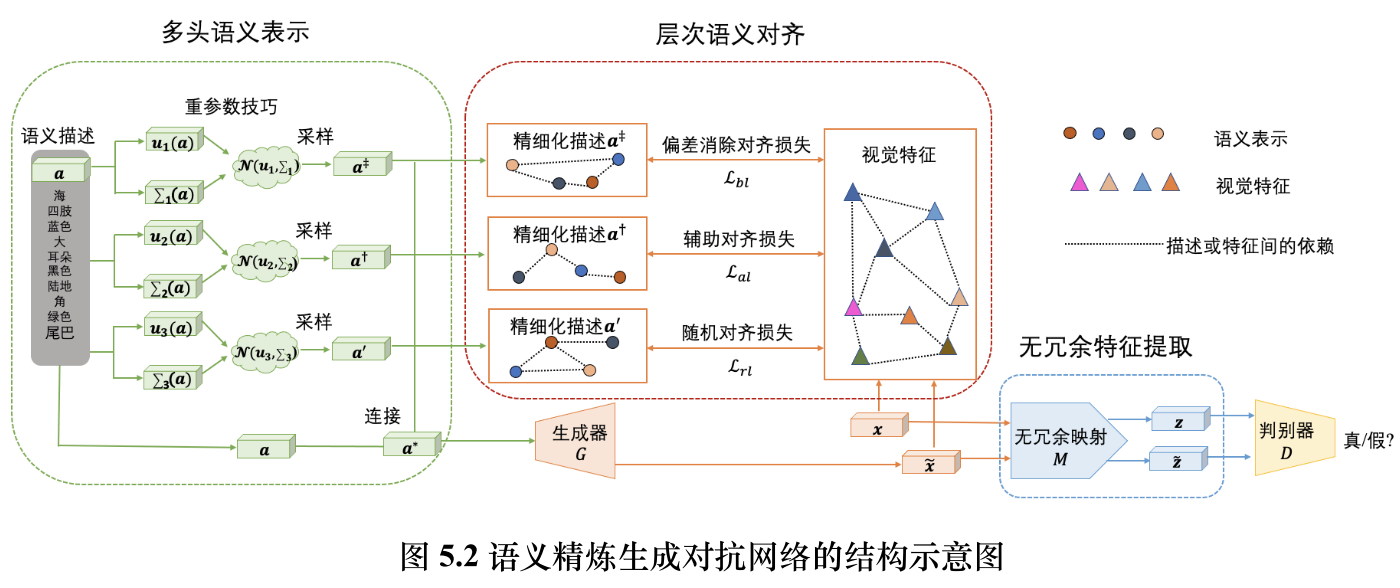
语义精炼生成对抗网络的目标是在对抗生成的框架下训练一个特征生成器 G ；该生成器的输入是拼接后的语义描述 a ∗ = [a ‡,a †,a ′,a ]，输出是虚拟特征 ˜x 。

从WGAN出发

在原始GAN中，判别器（D）的任务是区分真实图像和生成图像，它输出一个概率值（0到1之间）。生成器（G）的目标是“欺骗”判别器。

这带来了两个主要问题：

梯度消失（Vanishing Gradient）：当判别器训练得太好时，它能非常轻松地区分真假样本。此时，它提供给生成器的梯度（即“如何改进”的信号）会变得非常小甚至为零。生成器无法获得有效的学习信号，导致训练停滞。
模式崩溃（Mode Collapse）：生成器可能会发现只生成一种或少数几种能成功欺骗判别器的样本，然后不断重复生成这些样本，而无法学习到真实数据的完整分布。

WGAN 的核心思想是换一个更好的“尺子”来衡量真实数据分布和生成数据分布之间的差异。这把新尺子就是 Wasserstein 距离。

优点：即使两个分布完全没有重叠（比如两个土堆离得很远），Wasserstein 距离仍然能提供一个有意义的、平滑的数值，告诉我们它们相差多远。这个数值会随着两个分布逐渐接近而平滑地减小。

WGAN是如何实现的？

直接将Wasserstein距离公式用于GAN训练在计算上是困难的。WGAN的作者通过Kantorovich-Rubinstein 对偶性将其转化为一个可优化的形式。这导致了WGAN在实现上的两个关键改变：

关键改变一：判别器改为评论家（Critic）

在WGAN中，原来的“判别器”不再输出一个0到1的概率值来判断真假。它变成了一个评论家（Critic），其任务是学习一个函数 $f_w$ ，为真实图像输出一个较高的分数，为生成图像输出一个较低的分数。这个分数的差值（即真实样本得分与生成样本得分的期望差）就是Wasserstein距离的近似。

关键改变二：权重裁剪（Weight Clipping）

为了满足理论中对评论家函数 $f_w$ 必须是 1-Lipschitz 连续 的要求，最初的WGAN论文采用了一个简单的方法：将评论家的权重参数限制在一个固定的范围内（例如 [-0.01, 0.01]）。

这确保了评论家的输出变化不会太剧烈，从而满足了Lipschitz约束。

加入分类正则项

加入无冗余映射 M

学习一个映射函数 M，它能够将原始视觉特征 x_s 转换成一个“干净”的特征 z_s。这个干净特征 z_s 既要能很好地进行分类（由间隔损失 ℒ_m 保证），又要尽可能简洁、不冗余、抗噪声（由KL约束保证）。

$\mathcal{L}_{m}=\mathbb{E}_{p_{M}(z_{s}|x_{s})}[max(0,\bigtriangleup +\left \| z_{s}-c_{y} \right \| _{2}^{2} - \left \| z_{s}-c_{y'} \right \| _{2}^{2} )] \\ s.t. \mathbb{E}_{p_{M}(z_{s}|x_{s})} [D_{KL}[p_{M}(z_{s}|x_{s}) || r(z_{s})]] \le b$

首先，我们明确一下各个符号的含义：

x_s：原始视觉特征（输入）。通常是高维、可能含有噪声或冗余信息的特征。
M：映射函数（例如一个神经网络）。
z_s：提取后的“干净”特征（输出）。z_s = M(x_s)。
p_M(z_s | x_s)：条件分布。给定输入 x_s 时，输出 z_s 的分布。在确定性映射中（比如一个普通的神经网络），输入一个 x_s 会确定性地输出一个 z_s。此时，这个分布可以看作是一个以 M(x_s) 为中心的、非常尖锐的分布（例如方差极小的狄拉克分布）。这暗示映射 M 可能带有随机性（如Dropout），或者我们可以将其输出视为一个分布。
r(z_s)：先验分布。我们希望提取到的干净特征 z_s 所服从的理想分布。通常我们假设它是一个简单的标准分布，比如标准正态分布 N(0, I)。

c_y: 属于类别 y 的特征中心（可学习的参数）。
c_{y'}: 不属于类别 y 的某个其他类别的特征中心。
∆ (Delta): 边界超参数。
b: 一个常数，用于约束KL散度的上界。

间隔损失（Margin Loss）

ℒ_m = 𝔼_{p_M(z_s | x_s)} [ max(0, ∆ + ‖ z_s - c_y ‖²₂ - ‖ z_s - c_{y'} ‖²₂ ) ]

这一项的核心目的是拉近特征与其正确类别中心的距离，同时推远其与错误类别中心的距离。它借鉴了对比学习或三元组损失的思想。

‖ z_s - c_y ‖²₂: 这是特征 z_s 到其正确类别中心 c_y 的欧几里得距离的平方。映射 M 的学习目标是要让这个值越小越好。这意味着，属于同一类的特征应该聚集在它们的类别中心周围。
‖ z_s - c_{y'} ‖²₂: 这是特征 z_s 到某个错误类别中心 c_{y'} 的欧几里得距离的平方。映射 M 的学习目标是要让这个值越大越好。这意味着，不同类别的特征应该被分离开。
∆ + ‖ z_s - c_y ‖²₂ - ‖ z_s - c_{y'} ‖²₂: 这是整个表达式的核心。
- 我们希望 ‖ z_s - c_y ‖²₂ 不仅小于 ‖ z_s - c_{y'} ‖²₂，而且希望它们之间有一个安全间隔（Margin）。
- 具体来说，我们希望 ‖ z_s - c_{y'} ‖²₂ 比 ‖ z_s - c_y ‖²₂ 至少大 ∆。
- 如果这个差值已经大于等于0（即 ‖ z_s - c_{y'} ‖²₂ - ‖ z_s - c_y ‖²₂ ≥ ∆），说明间隔条件已经满足，那么 max(0, ...) 的结果为0，没有损失。
- 如果这个差值小于 ∆（即 ‖ z_s - c_{y'} ‖²₂ - ‖ z_s - c_y ‖²₂ < ∆），说明间隔条件未被满足，那么 ∆ + ... 的结果为正数，就会产生一个正的损失值，从而驱动模型更新参数来满足这个间隔要求。
max(0, ...): 这是Hinge Loss的标准形式。它意味着只有当间隔条件不被满足时，才会产生损失。这使训练更加稳定，只关注那些“难分的”或“距离不够远”的样本。
𝔼_{p_M(z_s | x_s)} [...]: 期望值表明，我们是在特征 z_s 的分布上计算这个损失的均值。这考虑到了映射 M 可能存在的随机性。

小结主体部分的作用：

最大化类间间隔，最小化类内距离。 确保提取的干净特征 z_s 在特征空间中有良好的可分性，同一类的特征紧密聚集，不同类的特征清晰分离。

KL散度约束（信息瓶颈）

s.t. 𝔼_{p_M(z_s | x_s)} [ D_KL[ p_M(z_s | x_s) || r(z_s) ] ] ≤ b

这是一个正则化约束，其思想来源于信息瓶颈理论。它的目的是防止映射 M 学习到一个“冗余”的表示。

D_KL[ p_M(z_s | x_s) || r(z_s) ]: 这是KL散度，衡量了条件分布 p_M(z_s | x_s) 与先验分布 r(z_s) 之间的差异。
- p_M(z_s | x_s): 是映射 M 产生的特征分布，它包含了来自输入 x_s 的信息。
- r(z_s): 通常被设定为一个简单的分布，比如标准正态分布 N(0, I)。它可以被看作是我们希望特征 z_s 最终应该遵循的“理想形态”。
KL散度的含义:
- KL散度越大，说明 M 产生的特征分布与简单的先验分布差别越大，意味着 z_s 中包含了更多关于特定输入 x_s 的“个性化”或“冗余”信息。
- KL散度越小，说明 z_s 的分布越接近简单的先验分布 r(z_s)，意味着 z_s 丢弃了 x_s 中的很多细节，只保留了最核心的、用于分类的信息。
约束 ≤ b:
- 这个约束强制要求，特征分布 p_M(z_s | x_s) 平均来说不能偏离先验分布 r(z_s) 太远。
- 常数 b 控制着约束的强度。b 越小，约束越强，意味着对信息的压缩越厉害。

小结约束部分的作用：

充当信息瓶颈，防止过拟合，提取更鲁棒的特征。 它强迫映射 M 学习一个“紧凑”的、“去冗余”的特征表示。z_s 只需要包含足够区分类别 y 的信息，而可以丢弃 x_s 中与任务无关的噪声和细节。这提高了特征的泛化能力。

修改损失函数

利用无冗余映射M，公式（5-15）可以被重写为：

总体目标函数

训练技巧

朴素的网络结构

前提是有一个成熟的用于特征提取的预训练模型，论文中为图像数据集。

1. 前提：“预训练卷积神经网络的深层特征通常用于执行欠数据任务”

预训练模型的强大能力：在大规模数据集（如ImageNet）上预训练的CNN（如ResNet, VGG），其深层特征具有极强的语义信息。浅层特征通常包含边缘、颜色等基础信息，而深层特征已经能够捕捉到“物体的一部分”、“整个物体”甚至“场景”等高级抽象概念。
“欠数据任务”的挑战：当我们的目标任务数据量很少时，如果直接从零开始训练一个深度网络，模型会因为参数过多、数据过少而极容易过拟合——即记住训练数据中的噪声和特定样本，而不是学习泛化规律。
解决方案：特征提取：为了解决欠数据问题，一个标准做法是将预训练CNN作为固定的“特征提取器”。我们把输入数据通过这个预训练网络，将其深层（通常是最后一个全连接层之前）的输出作为新特征。这些特征已经非常“高级”和“有区分度”，使得后续的分类或生成任务变得容易很多。

结论：由于输入特征（预训练CNN的深层特征）本身质量已经很高，任务的复杂性被大大降低了。

2. 推论：“因此，我们不需要使用深度学习的范式进行网络设计”

“深度学习的范式”：这里指的是为了解决复杂问题（如直接从原始像素中识别物体）而设计的非常深层的神经网络。深度是深度学习成功的关键，因为它允许模型构建从低到高的层次化特征。
为什么现在不需要？：因为最困难的“特征提取”工作已经由预训练CNN完成了。你的任务不再是“从像素到概念”，而是“从高级语义特征到最终输出”。这相当于你把一座高山（原始数据分布）已经用缆车（预训练模型）运到了接近山顶的位置，最后一段路只需要轻松步行即可，而不需要再修建一条盘山公路（深层网络）。

3. 实践：“所有模块，例如生成器和判别器，都只使用一层或两层模块实现”

这就是将上述思想付诸实践的具体设计。

生成器（Generator）：它的任务是将输入的特征（或噪声）转换为目标数据。如果输入已经是高级语义特征，生成器只需要学习一个相对简单的映射来重构或转换这些特征，而不需要从零开始生成复杂的纹理和结构。一个浅层网络足以胜任。
判别器（Discriminator）：它的任务是区分“真实特征/图像”和“生成的特征/图像”。由于输入特征已经非常抽象，判别器需要判断的差异不再是低级像素差异，而是更高级的分布差异。这也是一个相对简单的任务，浅层网络完全可以处理。

4. 优势：“这有助于加速训练过程和降低过度拟合风险”

这是采用浅层设计带来的两个直接好处：

加速训练过程
- 参数更少：层数越少，模型的可训练参数（Weights, Biases）就越少。
- 计算量更小：前向传播和反向传播的计算复杂度显著降低。
- 收敛更快：简单的模型优化曲面更平滑，更容易找到最优解，因此训练所需的迭代次数（Epoch）也更少。
降低过度拟合（Overfitting）风险
- 模型容量（Capacity）与数据量匹配：过拟合的根本原因是模型过于复杂（高容量），而数据量不足，导致模型“死记硬背”了训练数据。这是一个经典的偏差-方差权衡问题。
- 浅层网络是“低容量”模型：通过故意使用浅层网络，我们限制了模型的表达能力。这使得模型没有足够的能力去记忆训练数据中的噪声和无关细节，从而被迫学习数据中最核心、最泛化的规律。这与任务本身（欠数据）的需求完美匹配。