PyTorch深度学习实战【12】之基于RNN的自然语言处理入门

说明

• 本文学自菜菜老师深度学习课程，仅供交流和学习使用！

一 NLP初认

1.1 三种智能层次

• 在研究者追求人工智能的路上，有三种不同的智能层次：

1. 运算智能：让计算机拥有快速计算和记忆存储能力。
   • 硬件加速器，如GPU(图像处理单元)、TPU(张量处理单元)、ASICs(应用特定集成电路)
   • 并行计算，如多核处理器、分布式系统、超线程技术
   • 高效算法，如FFT(快速傅里叶变换)；内存和存储技术，如SSD、RAM
2. 感知智能：让计算机系统具备感知外部环境的能力。
   • 计算机视觉：卷积神经网络（CNN）和图像处理在内的一系列内容，应用于图像识别、目标检测、图像分割等。
   • 语音识别：技术包括递归神经网络（RNN）、长短时记忆网络(LSTM）、声谱图等。
   • 触觉技术：例如电容触摸屏、压力感应器等。
   • 其它传感器技术：如雷达、激光雷达（LiDAR）、红外线传感器、摄像头、麦克风等。
3. 认知智能：让计算机具备类似于人类认知和思维能力的能力。
   • 自然语言处理：如RNN、transformer、BERT、GPT架构、语义分析、情感分析等。
   • 增强学习：技术包括Q-learning、Deep QNetworks(DQN)、蒙特卡洛树搜索（MCTS）等。
   • 知识图谱：结合大量数据，构建对象之间的关系，支持更复杂的查询和推理。
   • 逻辑推理和符号计算：如专家系统、规则引l擎、SATsolvers等。
   • 模拟人类思维的框架和算法，如认知架构（如SOAR和ACT-R)。

---

• 认知智能是智能的终极体现，人机协同的交流是智能被实现的象征。
• 人工智能的终极评判标准就是人机协同交流。要实现人机协同交流的大目标，自然语言处理（Natural Language Process/NLP）必须实现，自然语言处理正式研究如何让计算机认知、理解、生成人类语言，甚至依赖这些语言与人进行交流。

1.2 NLP三大发展阶段

1. 探索阶段2011~2015(前transformer时代)：在AlphaGo和卷积网络掀起第三次人工智能革命之前，NLP领域主要依赖人工规则和知识库构建非常精细的"规则类语言模型”，当人工智能浪潮来临后，NLP转
   向使用统计学模型、深度学习模型和大规模语料库。在这个阶段，NLP领域的重要目标是“研发语言模型、找出能够处理语言数据的算法”。因此在这个阶段NLP领域学者们一直在尝试一些重要的技术和算法，如隐马尔可夫模型。
2. 提升阶段2015～2020（Transformer时代）：RNN和LSTM是非常有效的语言模型，但是和在视觉领域大放光彩的卷积网络比起来，RNN对语言的处理能力只能达到"小规模数据上勉强够用"的程度。2015年谷歌将自注意力机制发扬光大、提出Transformer架构，在未来的几年中，基于transformer的BERT、GPT等语言模型相继诞生，因此这个阶段NLP领域的重要目标是”大幅提升语言模型在自然语言理解和生成方面的能力”。这是自然语言处理理论发展最辉煌的时代之一。此外，这个阶段中语言模型已经能够很好地完成NLP领域方面的各个任务，因此工业界也实现了不少语言模型的应用，比如搜索引擎、推荐系统、自动翻译、智能助手等。
3. 应用阶段：2020-至今（大模型时代）：2020年秋天、GPT3.0所写的小软文在社交媒体上爆火，这个总参数量超出1750w、每运行1s就要消耗100w美元的大语言模型（Large Language Models，LLMs）为NLP领域开启了一个全新的阶段。在这一阶段，大规模预训练模型的出现改变了NLP的研究和应用方式，它充分利用了大规模未标注数据的信息，使得模型具备了更强的语言理解能力和泛化能力。基于预训练+微调模式诞生的大模型在许多NLP任务上取得了前所未有好成绩，在模型精度、模型泛化能力、复杂任务处理能力方面都展示出了难以超越的高水准，这吸引了大量资本的注意、同时也催生了NLP领域全新的发展方向与研究方向。

二 自然语言领域中的数据

• 在深度学习的世界中，某一领域的架构/算法往往是根据误领域中特定时数据状态设计出来的。如，为处理带有空间信息的图像数据，算法工程师们使用能够处理空间信息的卷积操作来创造卷积神经网络；如，为将充满噪音的数据转变成干净的数据，算法工程师们创造能够吞吃噪音、输出纯净数据的自动编码器结构。因此，在了解每个领域的算法架构之前，先学习当前领域的数据特点和数据结构。
• 在机器学习和普通深度神经网络的领域中所使用的数据是二维表。如在普通的二维表中，样本与样本之间是相互独立的，一个样本及其特征对应了唯一的标签，因此无论先训练1号样本、还是先训练7号样本、还是只训练数据集中的一部分样本，都不会从本质上改变数据的含义、许多时候也不会改变算法对数据的理解和学习结果。
• 但自然语言领域的核心数据是序列数据（一种在样本与样本之间存在特定顺序、且这种特定顺序不能被轻易修改的数据）。对序列数据来说，一旦调换样本顺序或样本发生缺失，数据的含义就会发生巨大变化。最典型的序列数据有以下几种类型

1. 文本数据（TextData）：文本数据中的样本的"特定顺序"是语义的顺序，词与词、句子与句子、段落与段落之间的顺序。在语义环境中，词语顺序的变化或词语的缺失可能会彻底改变语。如，事倍功半和事半功倍。在语义环境中，词语顺序的变化或词语的缺失可能彻底改变语义，例如，我（）她，当中间的内容不同时，句子的含义也会发生变化。
2. 时间序列数据（TimeSeriesData）：时间序列数据中的"特定顺序"就是时间顺序，时序数据中的每个样本就是每个时间点，在不同时间点上存在着不同的标签取值，且这些标签取值常常用于描述某个变量随时间变化的趋势，因此样本之间的顺序不能随意改变。例如，股票价格、气温记录和心电图等数据，一旦改变样本顺序，就会破坏当前趋势，影响对未来时间下的标签的预测。
3. 音频数据（AudioData）：音频数据大部分时候是文本数据的声音信号，此时音频数据中的"特定顺序"也是语义的顺序；当然，音频数据中的顺序也可能是音符的顺序，试想你将一首歌的旋律全部打乱再重新播放，那整首歌的旋律和听感就会完全丧失。
4. 视频数据（VideoData）：视频数据本质就是由一顿帧图像构成的，因此视频数据是图像按照特定顺序排列后构成的数据。和音频数据类似，如果将动画或电影中的画面顺序打乱再重新播放，那么难以能够理解视频的内容。

2.1 深度学习中的时间序列数据

• 主要给原始数据添加“时间顺序”或“位置顺序”，任意数据都可以转化为序列数据。

1. 二维单特征时间序列（time_step, 1）例如：1日天气

时间	气温
09:00	5
10:00	7
11:00	8
12:00	9

2. 二维多特征时间序列（time_step, input_dimensions）例如：一支股票的股价波动序列

时间	开盘价	收盘价	交易量	最高价	最低价
6月1日	0.8192	0.5303	12	0.0236	0.0122
6月2日	0.2031	0.2745	564	0.7803	0.5053
6月3日	0.452	0.7599	978	0.242	0.7992
6月4日	0.2078	0.8381	103	0.4569	0.3958

• 时间序列中，样本与样本之间的顺序就是时间序列，因此每个样本就是时间点。时间顺序是time_step上的顺序，在自然语言处理领域被称为“时间步”，它代表当前时间序列的长度，因此也被称为sequence_length。对时间序列而言，时间步的顺序是要求算法必须去学习的顺序。
• 在时序数据中，时间点可以是任意时间单位（分钟、小时、天），但时间点与时间点之间的间隔必须是一致的。
• 在nlp领域中，常常一次性处理多个时间序列。如一次性处理多支股票的股价波动序列：
  
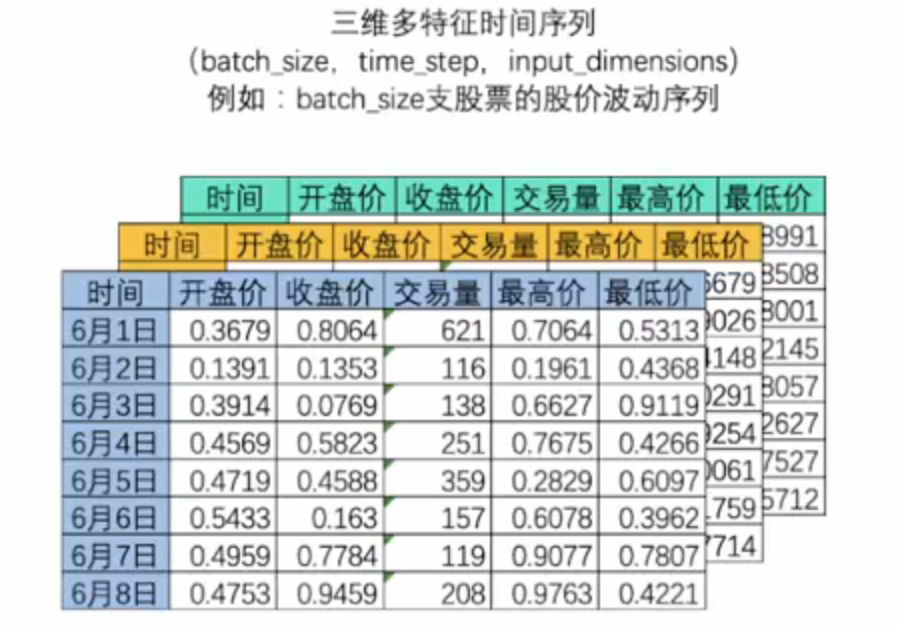
• batch_size：代表样本量，表示二位时间序列表单数量。
• 三位时间序列数据就是机器学习中定义的“多变量时间序列数据”，在多变量时间序列数据当中，时间和另一个因素共同决定唯一的特征值。如，上面的例子中，每张时序二维表代表一支股票，因此在这个多变量时间序列数据中"时间"和"股票编号”共同决定了一个时间点上的值。
• 在机器学习中，多变量时间序列数据结构如下：

股票ID	时间	开盘价	收盘价	交易量	最高价	最低价
00K621	6月1日	xxx	xxx	xxx	xxx	xxx
00K621	6月2日	xxx	xxx	xxx	xxx	xxx
00K621	6月3日	xxx	xxx	xxx	xxx	xxx
…	…	…	…	…	…	…
00E504	6月1日	xxx	xxx	xxx	xxx	xxx
00E504	6月2日	xxx	xxx	xxx	xxx	xxx
00E504	6月3日	xxx	xxx	xxx	xxx	xxx
…	…	…	…	…	…	…

2.2 深度学习中的文字序列数据

1. 二维单特征词向量（vocab_size, 1）

• 第一个编码表（例：“玉露凋伤枫树林”）

词	编码
玉	0.9337
露	0.8635
凋	0.3858
伤	0.7502
枫	0.6353
树	0.178
林	0.8483

• 第二个编码表（例：“小猫睡在毯子上因为它很暖”）

词	编码
小猫	0.6483
睡	0.5612
在	0.8261
毯子	0.499
上	0.2445
因为	0.0472
它	0.7753
很	0.9455
暖	0.3611

• 文字数据中，样本与样本之间的联系是语义的联系，语义的联系就是词与词之间、字与字之间的联系，因此在文字序列中每个样本是一个单词或一个字（或字母、半字），在中文文字数据中，一张二维表往往是一个句子或一段话，而单个样本则表示单词或字。
• 不能够打乱顺序的维度是vocab_size，它代表了一个句子/一段话中的字词总数量。一个句子或一段话越长，vocab_size也就会越大，因此这一维度的作用与时间序列中的time_step一致，vocab_size在许多时候也被称为是序列长度（sequence_length）。同样，vocab_size这一维度上的顺序就是算法需要学习的语义顺序。
• 算法不能认知文字数据，因此必须将文字数据转化为“数字”进行标识，这个过程就是编码。最形象的理解就是将一个单词编码成一个数字，也可以将单词编码成一个序列。当句子被编码成矩阵后，就会构成高维的多特征词向量。由于实际训练时，所有句子段落长度无法保证长度一致（即vocab_size都一致的可能性太小），因此往往将短句子进行填充，或将长句子进行裁剪，让所有的特征向量保持在同样的维度。
• 三维多特征向量（batch_size,vocab_size,input_dimensions）
  

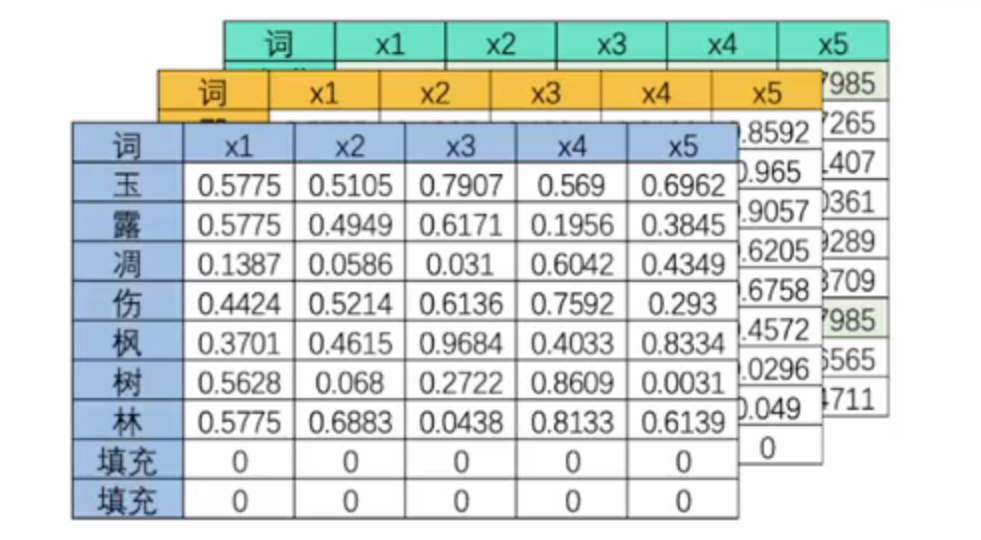
词	x1	x2	x3	x4	x5
玉	0.5775	0.5105	0.7907	0.569	0.6962
露	0.5775	0.4949	0.6171	0.1956	0.3845
凋	0.1387	0.0586	0.031	0.6042	0.4349
伤	0.4424	0.5214	0.6136	0.7592	0.293
枫	0.3701	0.4615	0.9684	0.4033	0.8334
树	0.5628	0.068	0.2722	0.8609	0.0031
林	0.5775	0.6883	0.0438	0.8133	0.6139
填充	0	0	0	0	0
填充	0	0	0	0	0

词	x1	x2	x3	x4	x5
小猫	0.9188	0.2104	0.1887	0.2186	0.7985
睡	0.5775	0.0393	0.886	0.6601	0.7265
在	0.1387	0.5956	0.146	0.3367	0.1407
毯子	0.4424	0.4284	0.1991	0.6272	0.0361
上	0.3701	0.3489	0.551	0.8456	0.9289
因为	0.5628	0.6547	0.5577	0.6331	0.3709
小猫	0.9188	0.2104	0.1887	0.2186	0.7985
很	0.3795	0.9319	0.5231	0.9104	0.6565
冷	0.183	0.9157	0.6825	0.3792	0.4711

2.2.1 中文分词操作

• 原始文本多为段落，但深度学习模型通常以词或字为输入样本，因此文字数据常需“分词”——将连续文本切分为有独立意义的词或词组。良好的分词能降低算法理解难度，提升模型性能。
• 例：诗句“玉露凋伤枫树林”，分作[“玉露”,“凋伤”,“枫树林”]（3个词）比拆为7个单字（如[“玉”,“露”,“凋”…]）更易理解，单个汉字较难自带完整语义。
  语言特性决定分词方式：
• 英文等拉丁语系：天然用空格分隔单词，按空格分词即可。
• 中文、日文、韩文等：无空格辅助，分词易引发歧义（即“断句”挑战）。
• 例：“吃烧烤不给你带”，分作[“吃”,“烧烤”,“不给”,“你”,“带”]与[“吃”,“烧烤”,“不”,“给你”,“带”]，语义不同。

---

中文分词方法

1. 基于词典：经典方法（如最大匹配法、最小匹配法），需预先构造词典。
2. 基于统计：如HMM（隐马尔可夫模型）、CRF（条件随机场）。
3. 深度学习：如基于Bi-LSTM的分词模型。

---

经典中文分词工具

1. jieba

• 定位：Python第三方库。
• 特点：支持精确模式、全模式、搜索引擎模式三种分词；速度快、使用简单，可自定义添加词典。

2. HanLP

• 定位：多功能NLP工具（不仅分词）。
• 功能：含分词、词性标注、命名实体识别等；支持CRF、感知机等多种算法及简繁体中文；提供丰富预处理与后处理功能。

3. THULAC（清华大学THU词法分析工具包）

• 功能：支持分词与词性标注。
• 技术：基于条件随机场（CRF）模型。

4. FudanNLP（复旦大学NLP工具集）

• 功能：提供分词、词性标注、命名实体识别等功能
• 技术：使用结构化感知机模型

5. LTP（语言技术平台）

• 功能：哈工大社会计算与信息检索研究中心开发。提供全套中文NLP处理工具，包括分词、词性标注、句法分析等。
• 技术：使用感知机模型

6. SNLP(stanford NLPfor Chinese)

• 功能：支持多种语言，其中包括中文。提供分词、词性标注、命名实体识别等功能。
• 技术：基于深度学习的方法

---

中文分词工具选择建议

• 工具选择需结合任务需求与场景：
• 简单文本预处理（多数基础场景）：jieba 足够，轻量易用。
• 深度语言学分析或高准确性需求：建议用 HanLP、LTP 等功能更全面的工具。

---

2.2.2 英文分词操作

• 空白符分词：利用英文单词与单词之间的空格分词。
• 基于规则的方法：图NLTK、spaCy等工具提供的分词方法。
• 子词分词：如BPE或SentencePiece，它们可以将英文单词进步切分为常见的字词或字符级别的片段。

2.2.2 词、字与token

• Token的定义：Token（读音tow·kn）是自然语言处理中的最小语义单元，具体形式随分词方式变化：
• 英文中：可为单词（如upstair）、半词（up, stair）、字母（u,p,s…）；
• 中文中：可为短语（如“攀登高峰”）、词语（“攀登”“高峰”）、单字（“攀”“登”“高”“峰”）。
• 分词与Token的关系：分词本质是分割Token的过程——将连续文本切分为独立语义单元（即Token），因此文字样本中的每一行可视为一个Token。
• 第一个编码表（例：“玉露凋伤枫树林”）

词	编码
玉	0.9337
露	0.8635
凋	0.3858
伤	0.7502
枫	0.6353
树	0.178
林	0.8483

词	编码
小猫	0.6483
睡	0.5612
在	0.8261
毯子	0.499
上	0.2445
因为	0.0472
它	0.7753
很	0.9455
暖	0.3611

---

• Token在自然语言处理中的意义

1. 基础语义单元与输入样本

• Token是语义的最小组成部分，也是多数深度学习算法的“单一样本”输入。

2. 影响资源与成本

• Token数量反映文本长度与数据量，直接决定算法所需资源（算力、时间、电力），进而影响模型开发、训练及调用成本。

3. NLP与大模型中的核心作用

• 计价与限制：如OpenAI等厂商按Token使用量计价和限制。
• 性能衡量：大模型训练/微调时的Token用量是性能评估指标之一。
• 标准计量单位：已成为NLP领域数据量与模型吞吐量的公认单位。

2.2.3 编码

• 编码的必要性与本质：文字序列无法直接输入算法，需编码为数字数据。编码本质是用单个数字或数字组合代表字/词，同一规则下相同字/词对应相同编码（数字数量由工程师决定）。

---

• 深度学习中常见编码方式：

1. One-hot编码

• 将每个词表示为长度等于词汇表大小的向量，仅对应词位置的维度为1，其余为0。

2. 词嵌入（Word Embeddings）

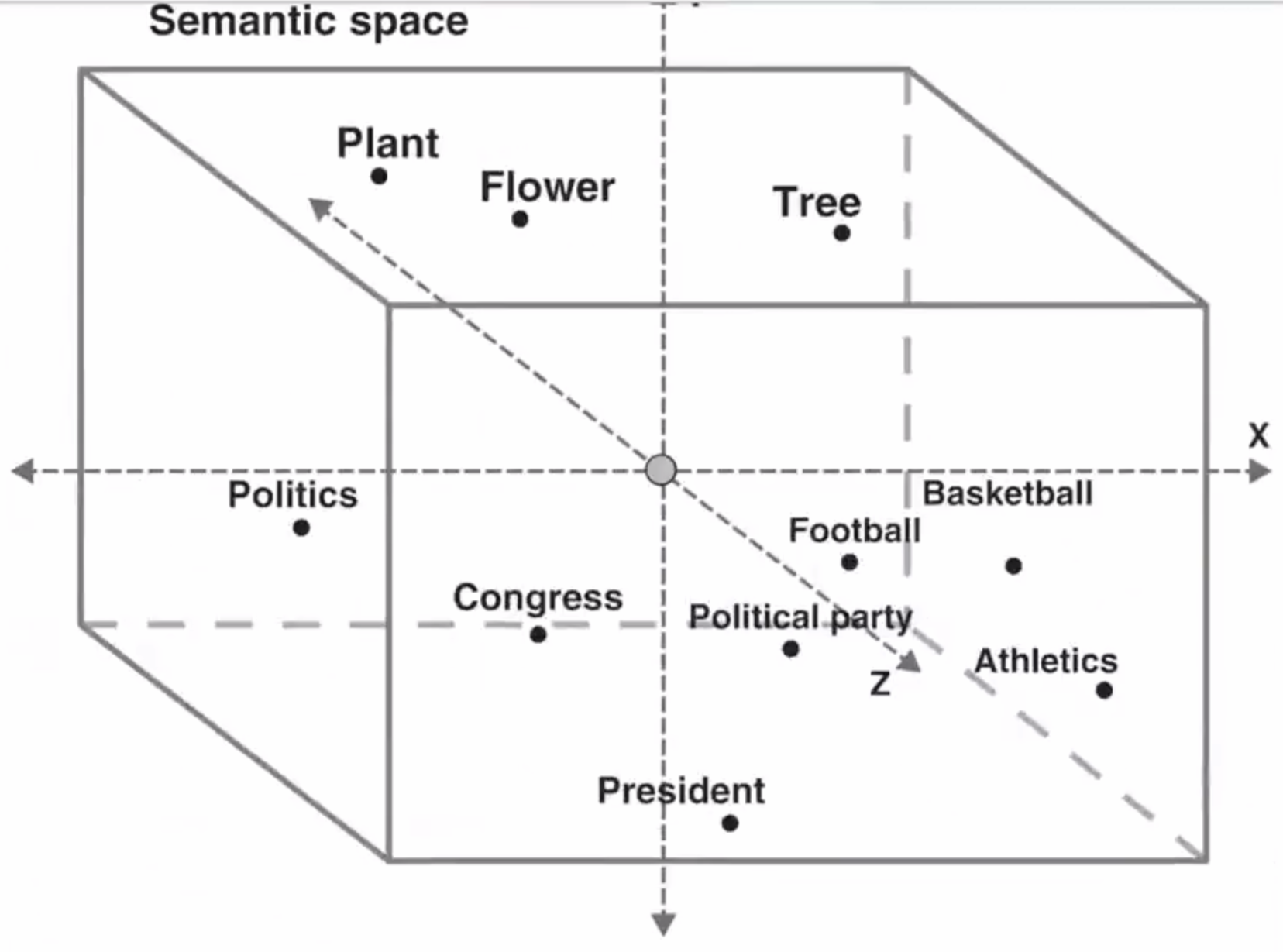
• 将词/短语映射到高维空间，使语义相似的词在空间中接近（如“king”与“queen”、“man”与“woman”）。
• 通过大量文本训练得到，目的是捕捉单词间的语义关系。

3. TF-IDF：基于单词在文档中的频率和在整个数据集中的反向文档频率来为单词分配权重。
4. BytePairEncoding（BPE)/ SentencePiece：子词级别的编码，能够处理词汇外的单词和多种语言的文本。
5. EIMo：深度上下文化词嵌入，考虑了单词的上下文信息来生成词向量。
6. Seq2Seq等序列变化模型：Seq2Seq（sequence-to-sequence）是一种序列转换模型，本质与encoder-decoder类似，输入和输出均为序列，广泛用于机器翻译、文本摘要、问答系统等任务。
   • 编码器过程：将输入序列（如句子）转换为固定大小向量，与文本编码逻辑相似。
   • 局限性：生成的向量通常为特定任务（如翻译）定制，不用于通用文本表示，与Word2Vec、TF-IDF等常规文本编码方法不同。

---

• 句子经Embedding与One-hot编码后的二维表对比

2.2.3.1 Embedding编码（二维多特征词向量）

词	x1	x2	x3	x4	x5
小猫	0.9188	0.2104	0.1887	0.2186	0.7985
睡	0.5775	0.6049	0.8017	0.1778	0.974
在	0.1387	0.4198	0.8978	0.3272	0.4131
毯子	0.4424	0.838	0.9486	0.7717	0.5491
上	0.3701	0.7075	0.7509	0.0047	0.2368
因为	0.5628	0.3516	0.8854	0.876	0.2108
小猫	0.9188	0.2104	0.1887	0.2186	0.7985
很	0.3795	0.3568	0.4526	0.0124	0.5528
冷	0.183	0.7371	0.2261	0.6636	0.8628

2.2.3.2 One-hot编码

词	x1	x2	x3	x4	x5	x6	x7	x8	x9
小猫	1	0	0	0	0	0	0	0	0
睡	0	1	0	0	0	0	0	0	0
在	0	0	1	0	0	0	0	0	0
毯子	0	0	0	1	0	0	0	0	0
上	0	0	0	0	1	0	0	0	0
因为	0	0	0	0	0	1	0	0	0
小猫	1	0	0	0	0	0	0	0	0
很	0	0	0	0	0	0	0	1	0
冷	0	0	0	0	0	0	0	0	1

说明：

• Embedding编码：将词映射为低维稠密向量（如5维），语义相似词向量接近（例：“小猫”重复出现时向量相同）。
• One-hot编码：为每个词分配独热向量（维度=词汇表大小），仅对应位置为1（例：“冷”对应x9=1）。

• 语义空间示例
  

2.2.4 经典词嵌入方法

1. Word2Vec

• 通过神经网络学习词向量，常见模型：CBOW、Skip-Gram。

2. GloVe（Global Vectors for Word Representation）

• 基于单词共现统计信息学习词向量。

3. FastText

• 类似Word2Vec，但额外考虑单词内部子词信息。

4. 固定编码

• 利用预训练模型（如BERT、GPT）编码文本，支持新任务微调。

5. 基于大语言模型的编码

• 如OpenAI生态中的专用embeddings大模型，用于构建语义空间。

三 循环神经网络

• 循环神经网络（RecurrentNeuralNetwork）是自然语言处理领域的入门级深度学习算法，也是序列数据处理方法的经典代表作，它开创了"记忆"方式、让神经网络可以学习样本之间的关联、它可以处理时间、文字、音频数据，也可以执行NLP领域最为经典的情感分析、机器翻译等工作。
• 在NLP领域，循环神经网络是GRU、LSTM以及许多经典算法的基础、更对理解transformer结构有巨大的帮助，因此即便在Transformer和大语言模型统治前沿算法战场的今天，依然需要学习RNN算法。
• NN就仿佛机器学习中的逻辑回归算法一般，是打开NLP领域大门的钥匙。

3.1 RNN的基本架构与数据流

• 循环神经网络由输入层、隐藏层和输出层构成，并且这三类层都是线性层。输入层的神经元个数由输入数据的特征数量决定，隐藏层数量和隐藏层上神经元的个数都可自己设置，而输出层的神经元数量则需要根据输出的任务目标进行设置。例如，将每个单词都编码成了5个特征构成的词向量，因此输入层就会需要5个神经元，将该文字数据输入循环神经网络执行三分类的"情感分类"任务（三分类分别是[积极，消极，中性]），那输出层就会需要三个神经元。假设有一个隐藏层，而隐藏层上有2个神经元，一个最为简单的循环网络的网络结构如下：
  
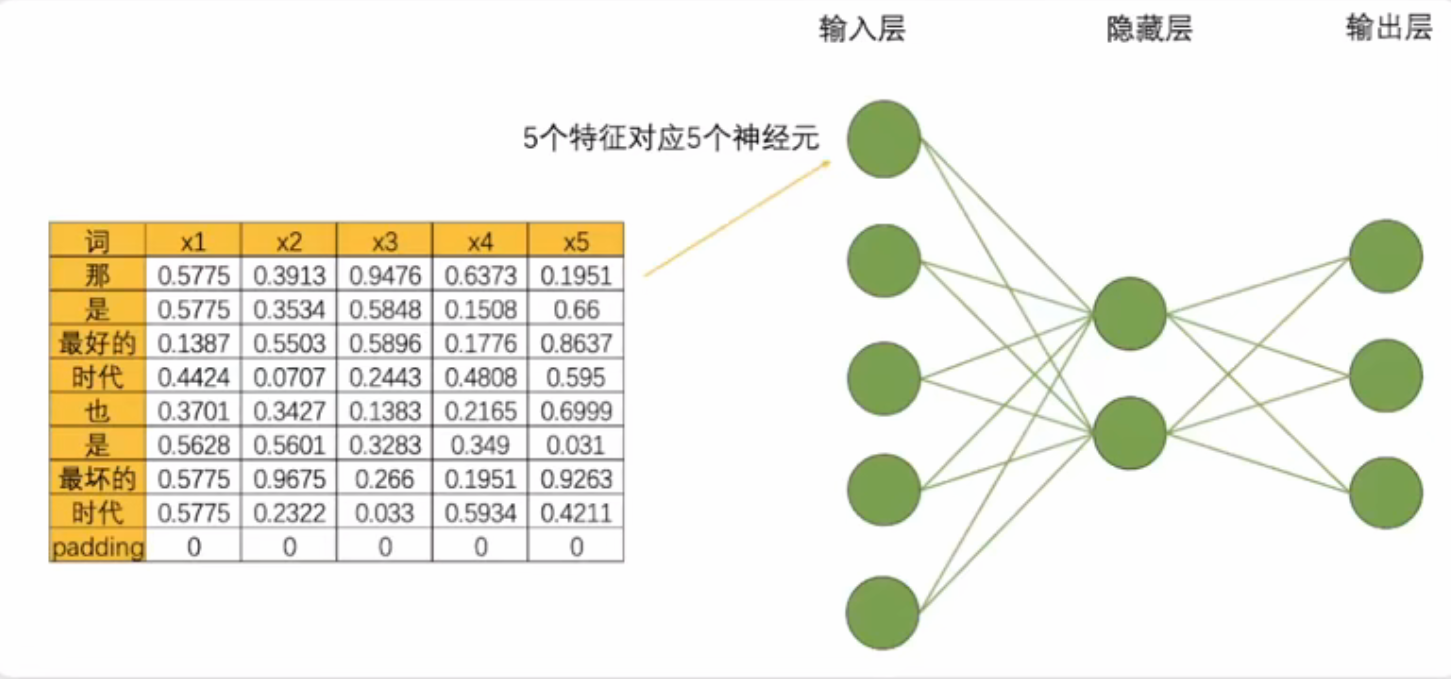
  RNN的基础网络构建与DNN一致，但其革命性在于设计了循环的数据流来处理序列数据。
• DNN方式：并行处理。例如，一次处理9个单词的序列，输入维度(9,5)经网络计算后输出(9,3)。该过程高效但完全忽略了单词之间的顺序和联系。
  
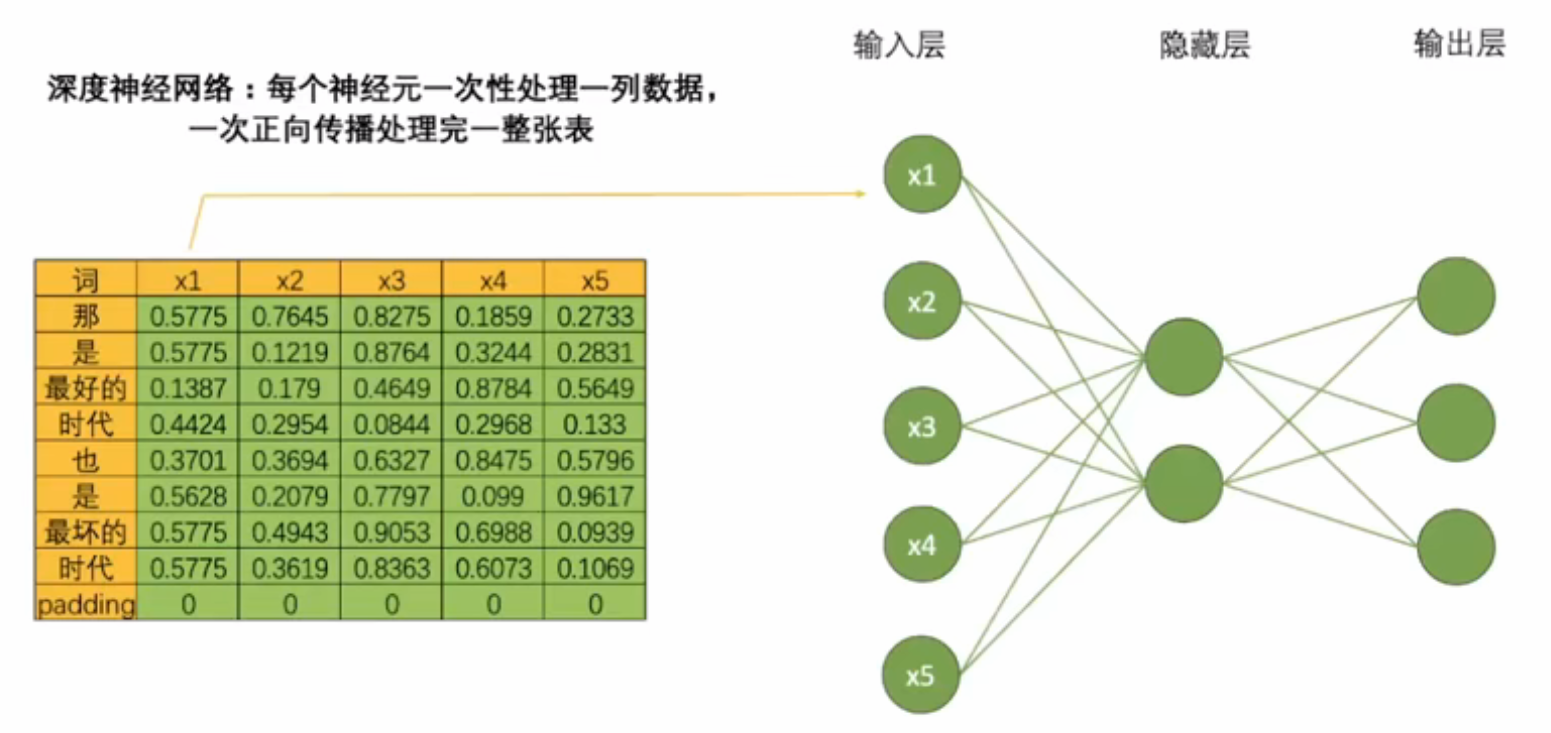
• RNN方式：顺序处理。通过循环单元逐个处理单词，使网络能够学习并记忆序列中的上下文信息。
  
  
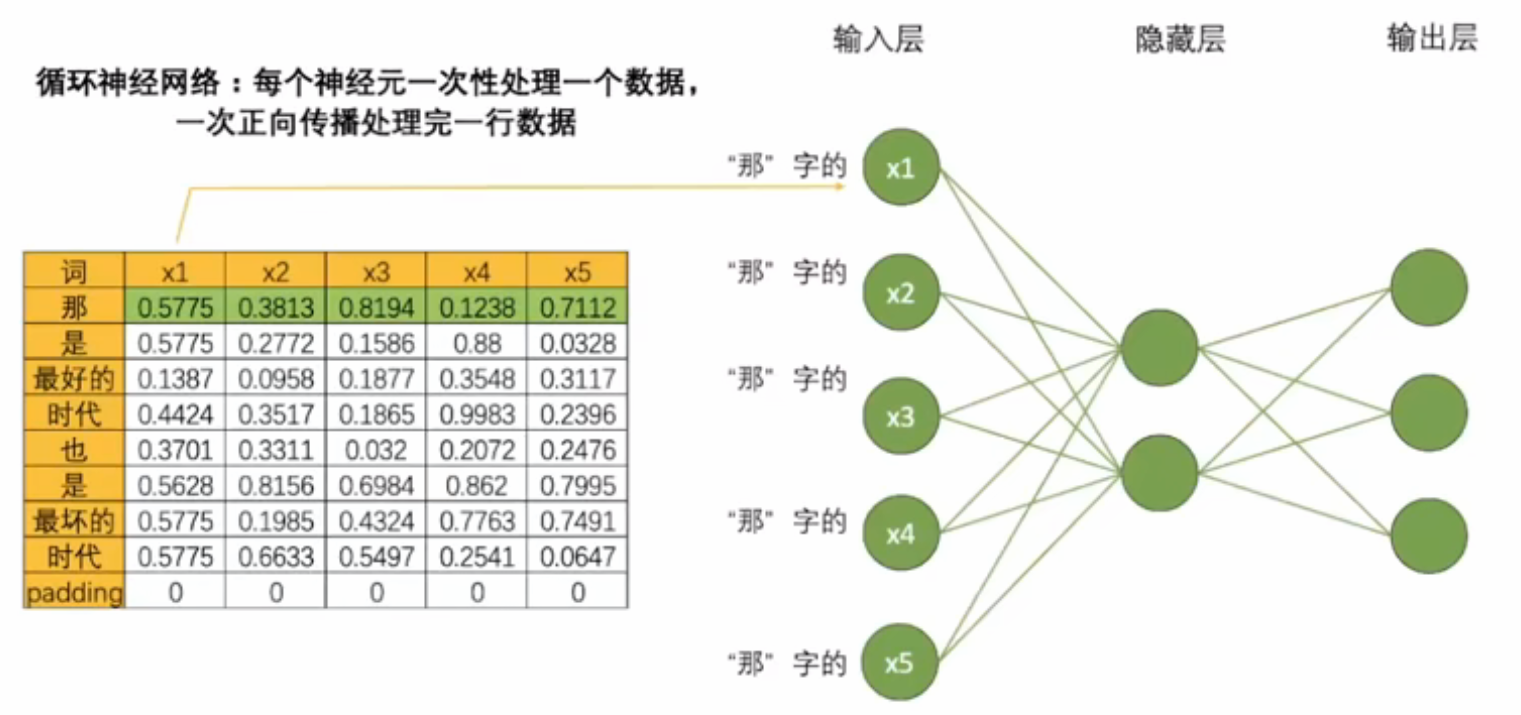
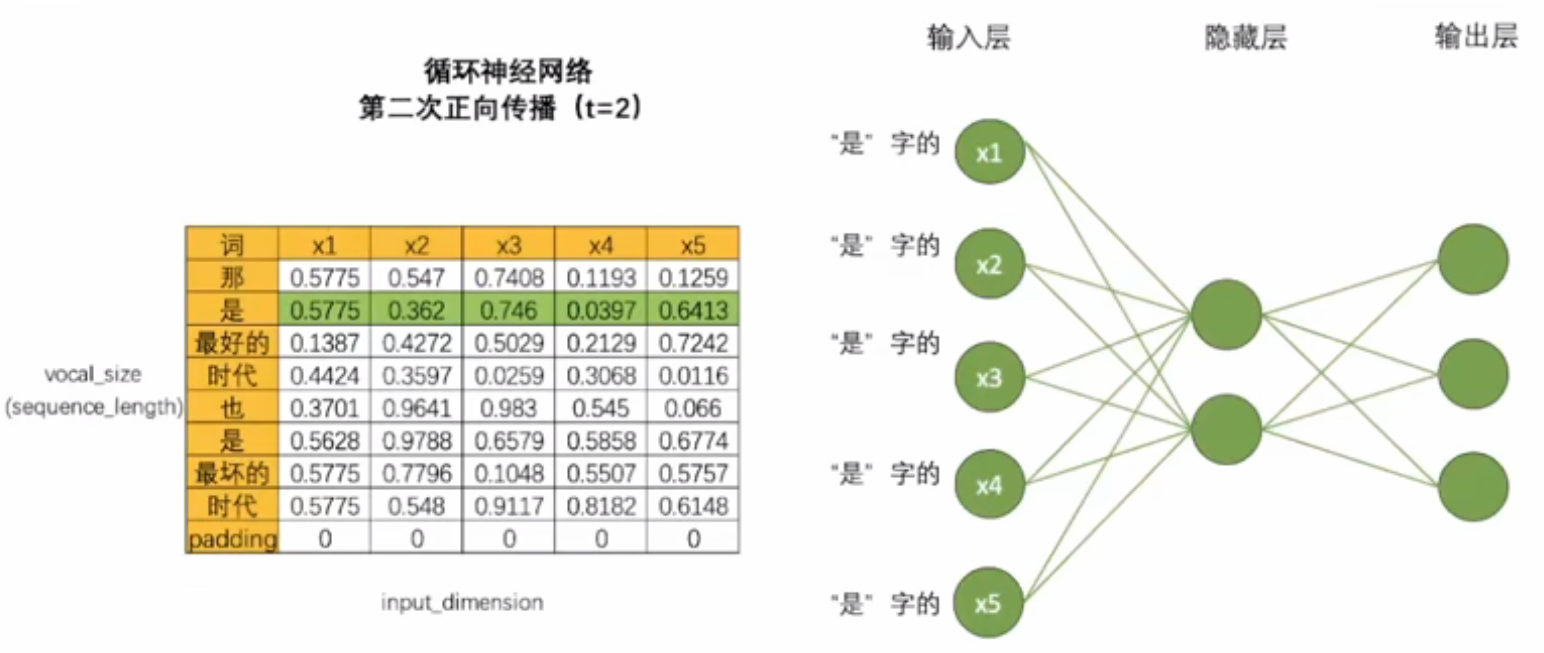
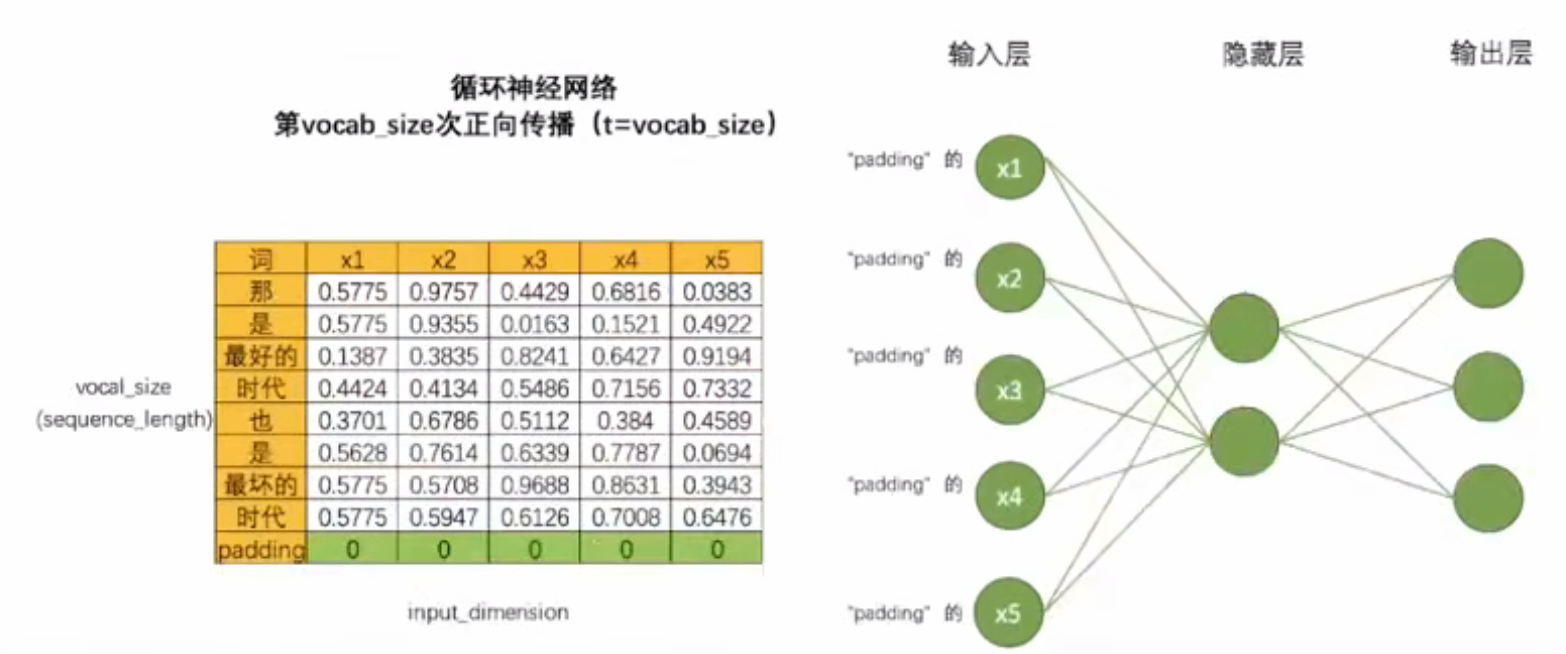
• 如果一次正向传播只能处理一行数据，对结构为(vocab_size,input_dimension)的文字数据来说，需要在同一个网络上进行vocab_size次正向传播。对于结构为(time_step,input_dimension)的时间序列数据来说，需要在同一个网络上进行time_step次正向传播。为了方便，vocab_size和time_step都统称为时间步。对任意数据来说，循环神经网络都需要进行时间步次正向传播，而每个时间步上是一个单词或一个时间点的数据。
• 这样数据流设置使循环神经网络构建了自己的灵魂结构：循环数据流。在多次进行正向传播的过程中，循环神经网络会将每个单词的信息向下传递给下一个单词，从而让网络在处理下一个单词时，还能记住上一个单词的信息。

---

• 如下图所示，循环网络通过时间步传递信息：
• $T_{t-1}$时间步：隐藏层输出$H_{t-1}$分两路：一路传向输出层$Y_{t-1}$，另一路留存给下一时间步。
• $T_t$时间步：隐藏层结合当前输入$X_t$和上一步留存的$H_{t-1}$，计算出包含历史信息的当前隐藏层输出$H_t$。
  

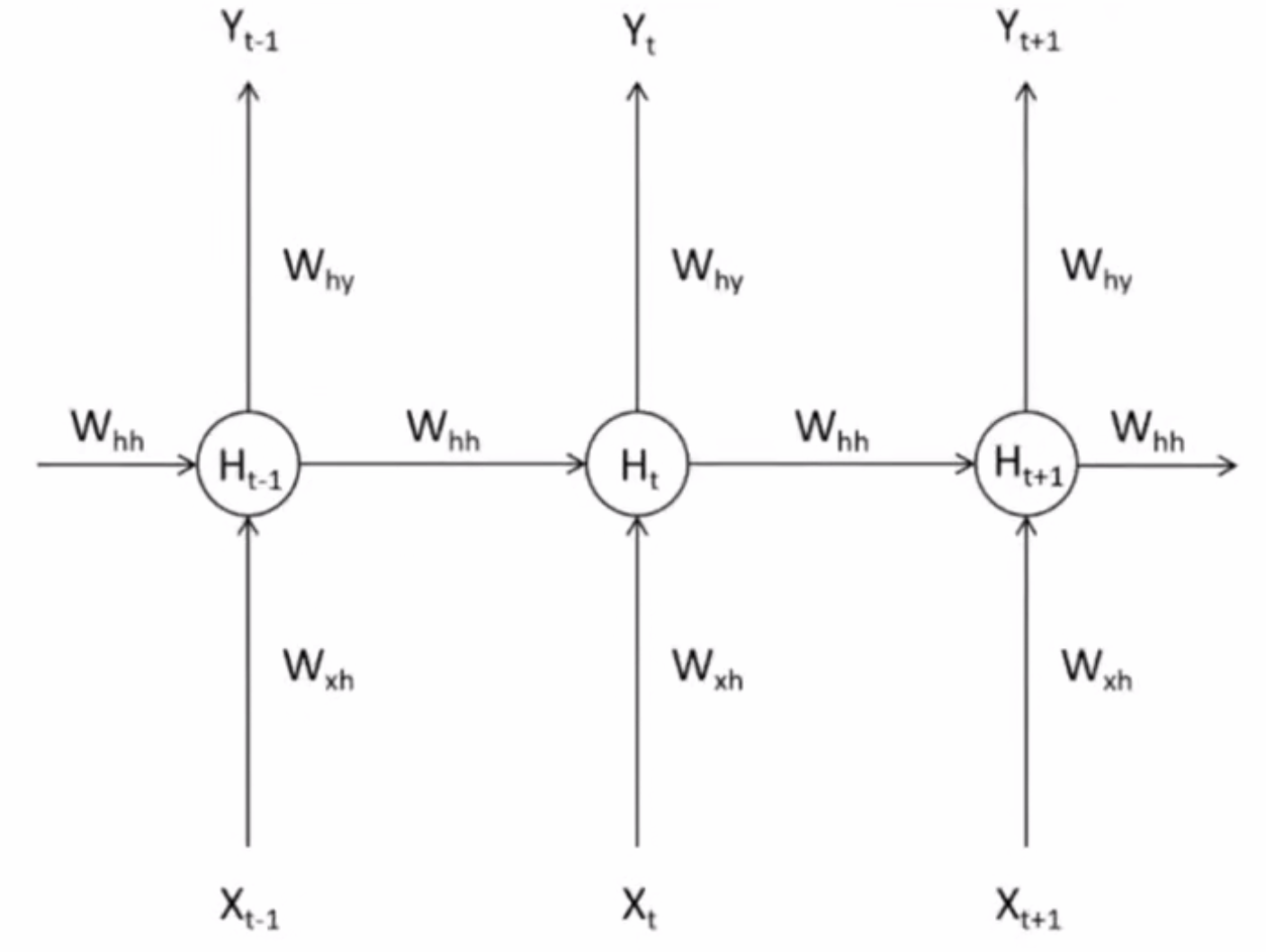
• H被称为隐藏状态(Hidden Representation或Hidden State)，特指在循环神经网络的隐藏状态上诞生的中间变量，一般在代码中也用小写字母h表示。

• 循环神经网络（RNN）中隐藏状态 $H_t$ 的递归展开，通过逐步代入前一时刻的隐藏状态表达式，体现了RNN对序列数据的记忆特性。
  $$\begin{array}{rl}{H}_t& =f(W_{hh}{H}_{t-1}+W_{xh}{X}_t)\\ & =f(W_{hh}f(W_{hh}{H}_{t-2}+W_{xh}{X}_{t-1})+W_{xh}{X}_t)\\ & =f(W_{hh}f(W_{hh}f(W_{hh}{H}_{t-3}+W_{xh}{X}_{t-2})+W_{xh}{X}_{t-1})+W_{xh}{X}_t)\\ & ...\end{array}$$
• $H_t$ 表示时刻 $t$ 的隐藏状态
• $X_t$ 表示时刻 $t$ 的输入
• $W_{hh}$ 和 $W_{xh}$ 分别是隐藏状态之间和输入到隐藏状态的权重矩阵
• $f(\cdot )$ 是激活函数
• 最后的省略号($...$）表示该递归过程可以继续向前展开到初始时刻

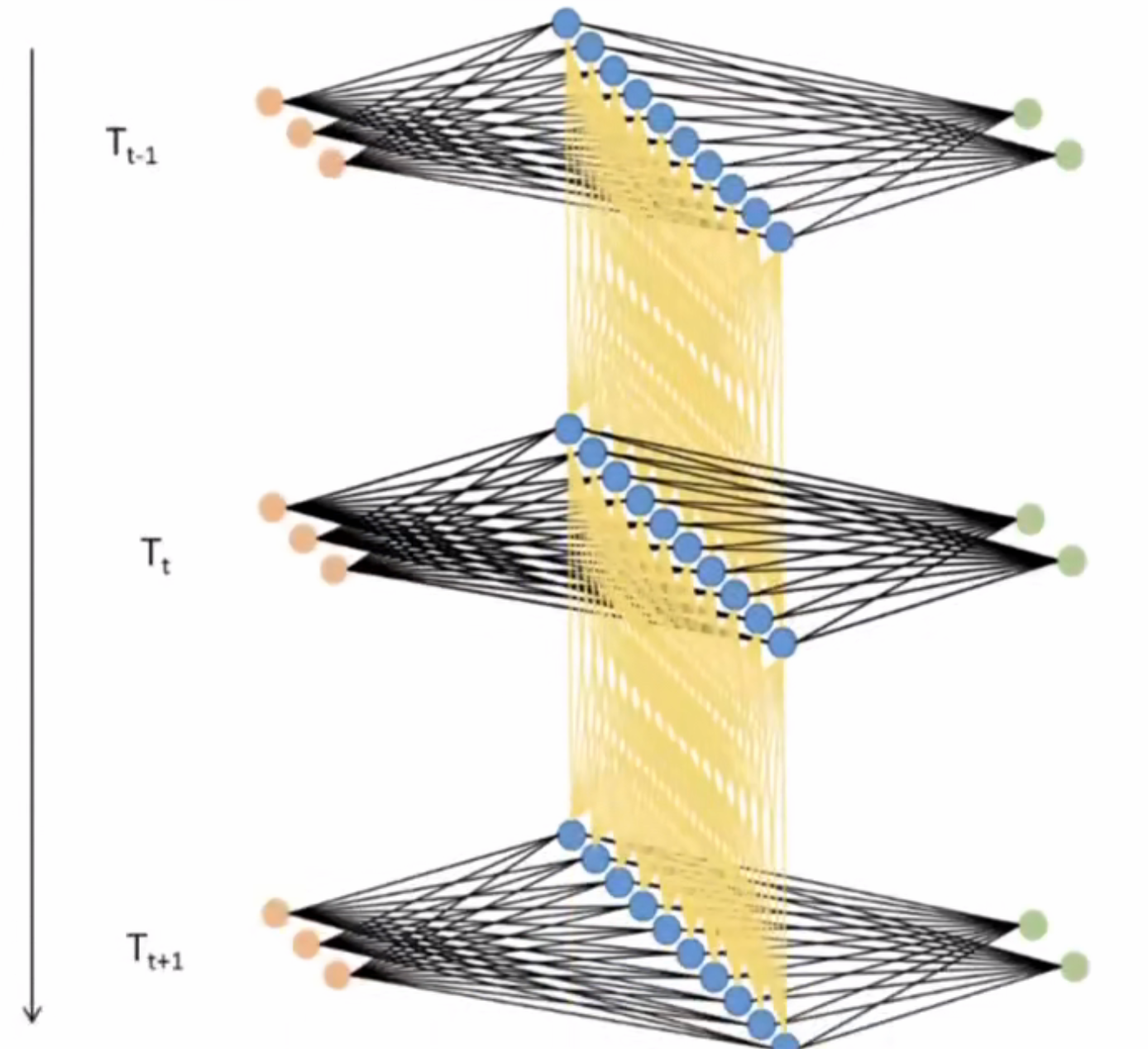
• 利用这种方式，只要进行vocal_size次向前传播，并且每次都将上个间步中隐藏层上诞生的中间变量传递给下一个时间步的隐藏层，整个网络就能在全部的正向传播完成后获得整个句子上的全部信息。在这个过程中，在同一个网络上不断运行正向传播，此过程在神经网络结构上是循环，在数学逻辑上是递归，这也是循环神经网络名称的由来。

3.2 RNN的效率问题与权值共享

• 循环神经网络由于每次只处理一行数据，一张表单就需要运行$Datc{h}_{s}ize\times tim{e}_{s}tep$次向前传播，导致整个网络运行效率极低。但是，现实中我们使用循环神经网络时，通过先编码每张二维表需要循环的时间步数量相等，对全部表单的每一行进行一一处理，最终循环神经网络只会进行time_step次向前传播，batch是共享权值的。
  
  

---

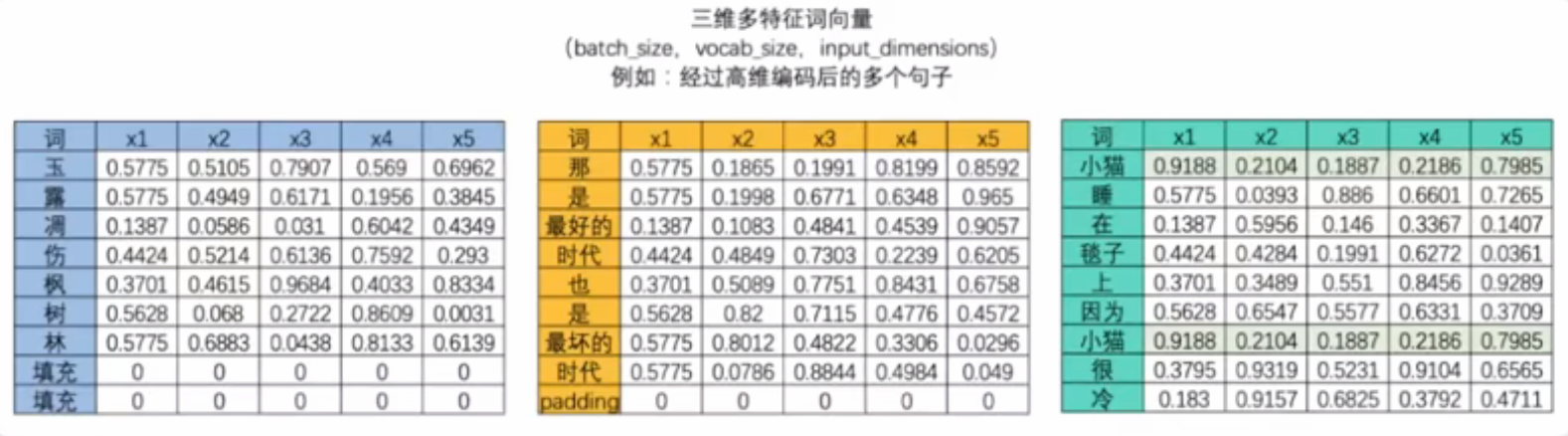
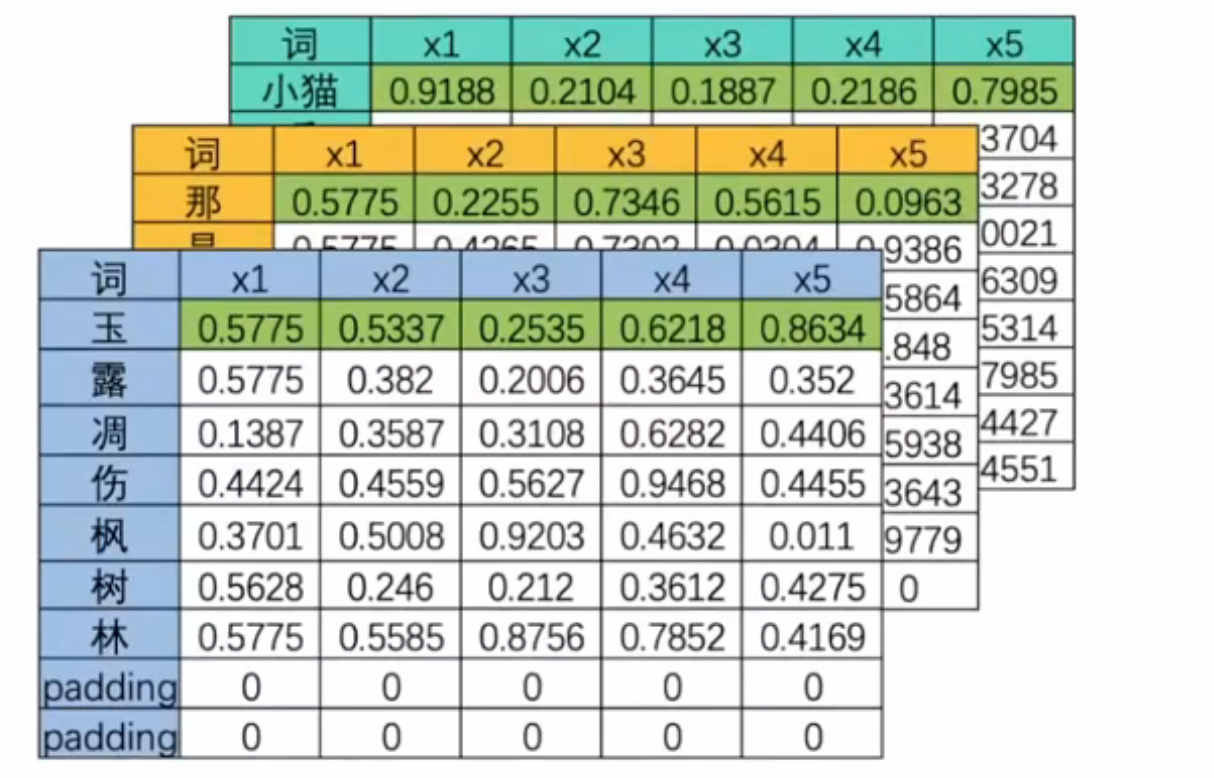
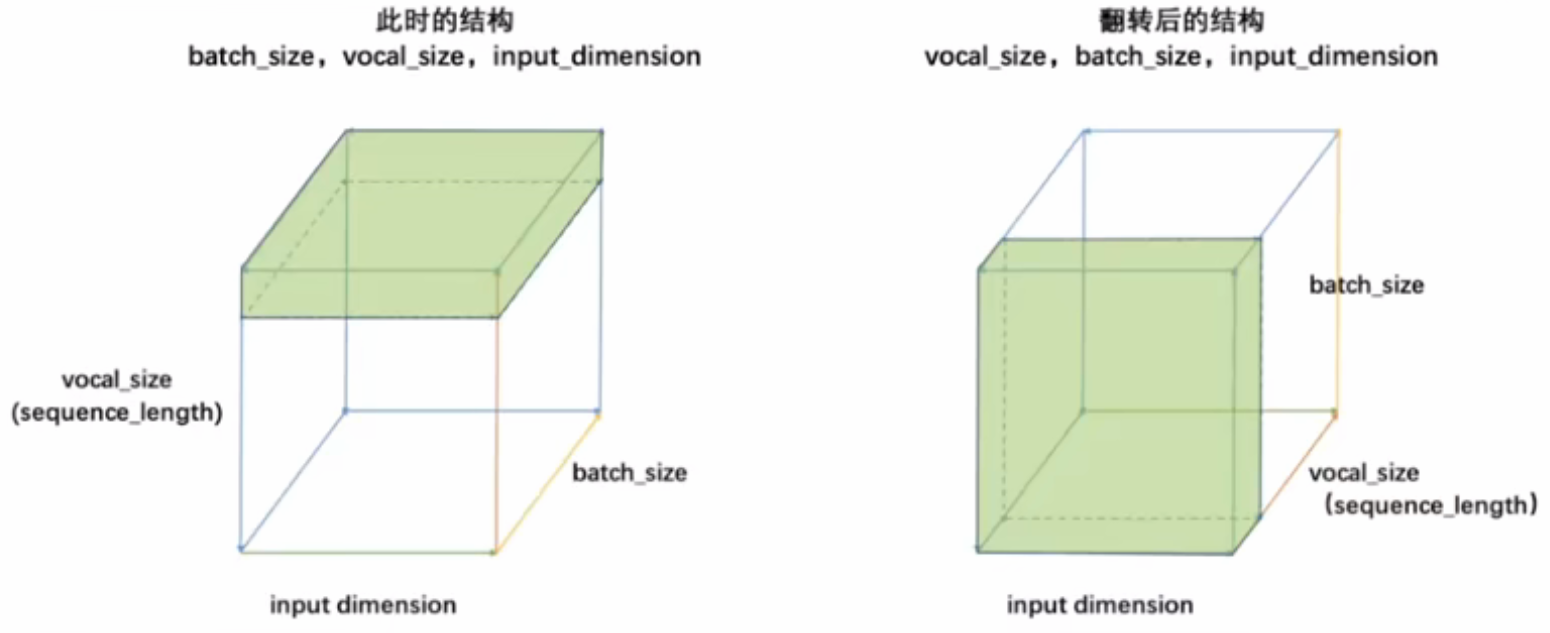
• 将三维数据看作立方体，循环神经网络就是一次性处理位于最上层的一整个平面数据，因此循环神经网络一次性处理的数据结构和深度神经网络一样都是二维的，数据结构为(batch_size,input_dimension)。
  

3.3 RNN的输入与输出格式

• 循环神经网络是为数不多的、能够在不改变网络结构情况下同时处理二维数据和三维数据的网络，但在PyTorch或tensorflow这样的深度学习框架的要求下，循环神经网络的输入结构一律为三维数据。

3.3.1 输入结构

• 通常来说，最常见的输入结构分为（batch_size，vocal_size，input_dimension，循环是在vocal_size维度进行）和为（vocal_size，batch_size,input_dimension，循环是在vocal_size维度进行）结构。
  

3.3.2 输出结构

• 循环神经网络的输出层结构是由具体的输出任务决定，但丰富的NLP任务让RNN输出层也变得丰富多彩。NLP任务分类（基于网络结构）：

1. 语义/关系/文字分类标注任务
   • 任务类型：文本分类（情感分析、新闻分类）、命名实体识别（NER）、关系抽取、词性标注、依存句法分析、核心指代消解
   • 技术特点：RNN输出层神经元数=标签类别数，损失函数常用交叉熵、Hinge损失，标注/NER任务可用Dice损失、CRF损失
2. 时序/语义分类回归任务
   • 任务类型：文本匹配（相似度计算、自动问答评分）、时序预测（趋势变化、未来行为预测）
   • 技术特点：输出层神经元数量灵活，根据预测需求设定（单步多时间点、多步单值、多行为分类等）
3. 序列到序列/生成式任务
   • 任务类型：文本生成（诗歌、故事）、图文生成/语音识别、问答/对话系统、摘要生成、机器翻译
   • 技术特点：基于输入序列生成目标序列，适用于创造性生成和转换任务

• NLP预测任务中，生成式流程比分类/回归任务更复杂。生成式任务中，RNN逐字或逐词生成句子或段落（如ChatGPT逐词输出），其输出层结构与分类任务存在显著差异。生成模型无法"无中生有"，只能从已见过的字、词或短语中选择语义自洽的输出。其本质是为每个候选字、词或短语计算概率，选择可能性最高的输出，因此属于多分类概率模型。

• 在NLP中，模型处理的数据来源于训练集构建的词汇表。数据预处理包括分词和编码，生成包含所有不重复字/词/短语的完整词汇表。词汇表大小（vocab_size）直接决定生成式任务输出层神经元数量——输出层神经元数与词汇表大小相等，每个神经元对应一个可能的字/词，其输出值表示该位置被预测为下一个字/词的概率，模型据此选择概率最高的词进行输出。

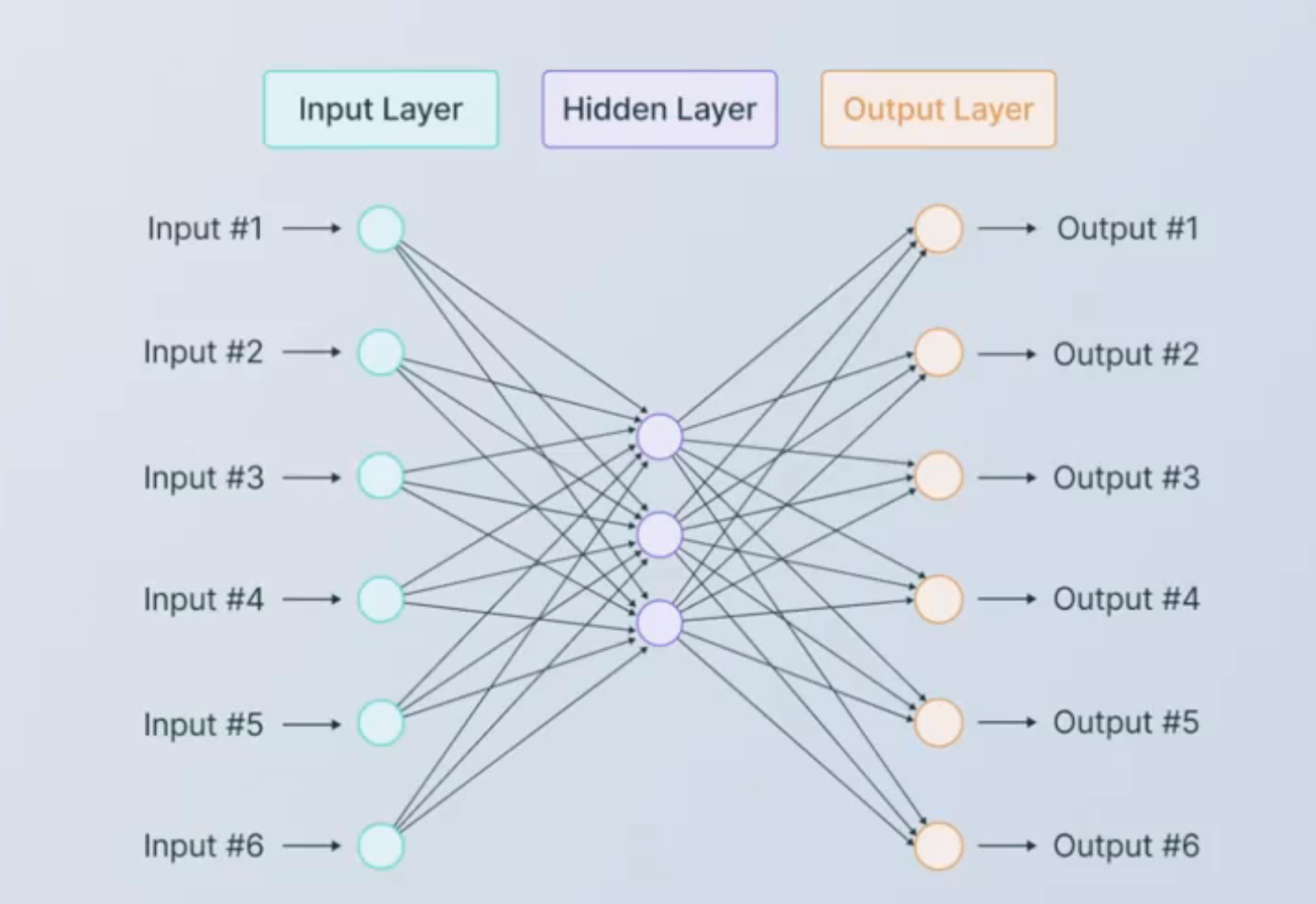
• 一个生成式模型想要进行灵活、丰富的文字生成，就必须先见过巨量文字数据。 同时，分词越细致，生成式模型在生成时的创造力就会越强。如果模型是基于字符级别的，那么输出层的神经元数量就是所有可能字符的数量，模型就可能基于字符构建新的词语。如果模型是基于词级别的，那么输出层的神经元数量就是词汇表中所有词的数量，模型就可能基于词语构建新的短语。

四 Pytorch实现DRNN架构

4.1 回顾：torch框架

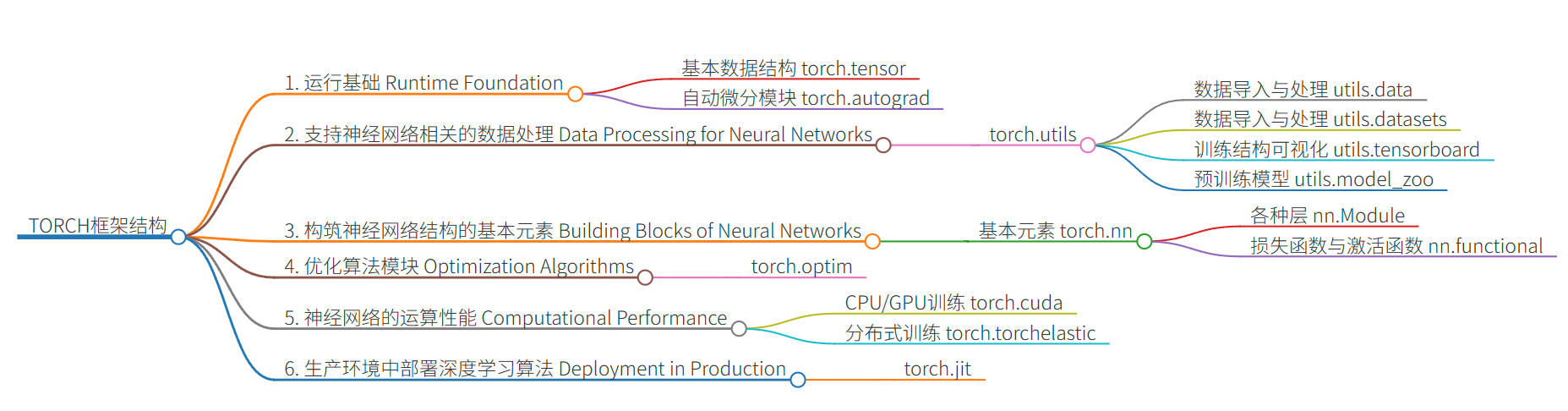
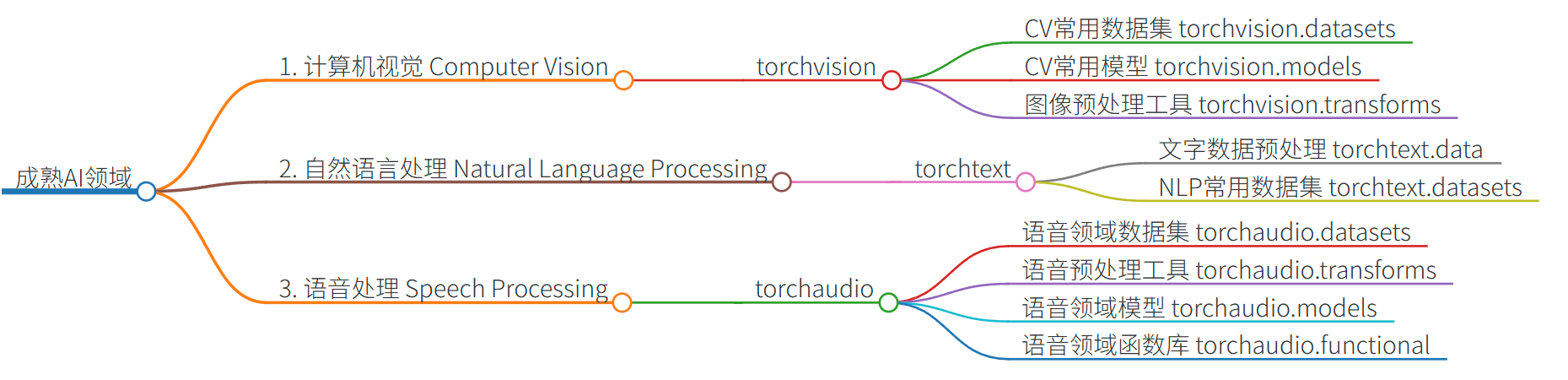
• 整个Pytorch框架可以大致被分为Torch和成熟AI领域两个板块，其中Torch包含各类神经网络组成元素、用于构建各类神经网络，各类AI领域中则包含Torchvision、Torchtext、Torchaudio等辅助完成图像、文字、语音方面各类任务的领域模块。
  
  

4.2 torch.nn输入、输出参数详解

• 在NLP世界中，torch.nn常用的各类经典元素：

1. 词嵌入层EmbeddingLayers:torch.nn.mbedding:用于将离散的词汇ID转换为连续的词向量。注意，普通的Embedding层与Word2Vec，GloVe等方法有巨大的区别。
2. 用于处理序列数据的各类神经网络层：torch.nn.RNN，torch.nn.LSTM和torch.nn.GRU等。对RNN来说，可以使用nn.Linear来替代nn.RNN，二者的网络结构是完全一样的，只要将数据流设置正确，torch.nn.RNN和torch.nn.Linear有时可以实现完全一致的效果。
3. 服务于Transformer架构的各类神经网络层和模型：例如nn.Transformer、nn.TransformerEncoder、nn.TransformerDecoder、nn.TransformerEncoderLayer、nn.TransformerDecoderLayer、nn.MultiheadAttention等。
4. 在文本任务中常常出现的各类损失函数：在各种NLP任务场景下都可以使用的交叉熵损失torch.nn.CrossEntropyLoss、均方误差nn.MSELoss、合页损失nn.MarginRankingLoss等损失函数。

---

class torch.nn.RNN(input_size,hiddent_size,num_layers,nonlinearity,bias,batch_first,dropout,bidirectional,*args,**kwargs)

• nn.RNN 是一个参数较少的简单循环层，在线性层基础上增加了时间步间传递功能。

• 主要功能：处理权重匹配、神经元加和、激活函数、前后传播，并将上一时间步的中间变量传递给下一时间步。
  关键参数：

• input_size：输入特征数量（输入层神经元数）。

• hidden_size：隐藏层神经元数（隐藏状态特征数）。

• nonlinearity：激活函数，可选 'tanh' 或 'relu'。

• batch_first：控制输入/输出 Tensor 形状。

  • True：[batch_size, seq_len, input_dimension]
  • False（默认）：[seq_len, batch_size, input_dimension]
  • seq_len：对应时间序列的 time_step 或文本序列的 vocab_size。

• RNN类有两个输出：

  • output：代表所有时间步上最后一个隐藏层上输出的隐藏状态的集合。output的形状为$[se{q}_{l}en,batc{h}_{s}ize,hidde{n}_{s}ize]$，不受隐藏状态影响。
  • hn：最后一个时间步的、所有隐藏层上的隐藏状态。形状为$[nu{m}_{l}ayers,batc{h}_{s}ize,hidde{n}_{s}ize]$。

• 虽然每个时间步和隐藏层都产生隐藏状态，但RNN类仅“选择性”输出部分隐藏状态（例如output保留最后一个隐藏层的隐藏状态，hn保留最后一个时间步的隐藏状态）。实际上，实现RNN时所有隐藏状态都会传递到下一时间步和下一隐藏层，因此output和hn都不能代表RNN层在循环过程中传输的全部信息。

• output关注全部时间步，hn关注全部隐藏层。如果需要执行对每个时间步进行预测的任务(如，预测每一分钟的股价，预测每个单词的词性)，需要关注的是每个时间步在最后一个隐藏层的输出，需要关注整个output；如果需要执行的是对每个表单、每个句子进行预测任务，如对句子进行情感分类，预测某个时间段内用户的行为，只需要关注最后一个时间步的输出。

• 有关output和hn的深刻理解参看深刻理解PyTorch中RNN（循环神经网络）的output和hn

import torch
from torch import nn
# seq_len/vocal_size = 3, batch_size=50, input_dimension=10
inputs = torch.randn((3, 50, 10))rnn1 = nn.RNN(input_size=10, hidden_size=20)
outputs1, hn1 = rnn1(inputs)print(outputs1.shape)  # 包含全部时间步上的隐藏状态
print(hn1.shape)  # 最后一个时间步，隐藏层上50个batch下，20个神经元上的数据
print(outputs1[-1, 0, :])
print(hn1[:, 0, :])

torch.Size([3, 50, 20])
torch.Size([1, 50, 20])
tensor([ 0.3507, -0.2680,  0.7556,  0.3783,  0.1110, -0.3633, -0.7336, -0.4555,-0.4843, -0.2489, -0.2412, -0.2417, -0.1569,  0.4327, -0.4055, -0.2606,0.2054, -0.3326,  0.5036,  0.6039], grad_fn=<SliceBackward0>)
tensor([[ 0.3507, -0.2680,  0.7556,  0.3783,  0.1110, -0.3633, -0.7336, -0.4555,-0.4843, -0.2489, -0.2412, -0.2417, -0.1569,  0.4327, -0.4055, -0.2606,0.2054, -0.3326,  0.5036,  0.6039]], grad_fn=<SliceBackward0>)

• 既然hn可从outputs中索引得到，为何nn.RNN还要单独设置hn作为输出？
• 原因有二：一是工程便利性——许多任务（如句子预测、生成式任务）只需关注最后一个时间步的隐藏状态，单独输出hn能直接获取该状态，省去用户自行提取的步骤；二是复杂架构适配——双向RNN、多层RNN等复杂结构中，直接调用hn比操作outputs更便捷。此外，运行nn.RNN时会自动执行多次循环（如示例中3次），可通过增大seq_len观察运行时间变化来判断循环是否真实进行。

4.3 深度循环神经网络

• 深度循环神经网络相较于普通的循环神经网络，拥有多个隐藏层。
• nn.RNN中通过num_layers指定隐藏层的层数，hidden_size指定隐藏层的神经元的数量，在Pytorch中每个隐藏层的尺寸都是相同的（简化模型的设计和超参数的调整）。

import torch
from torch import nn
# seq_len/vocal_size = 3, batch_size=50, input_dimension=10
inputs = torch.randn((3, 50, 10))drnn1 = nn.RNN(input_size=10, num_layers=4, hidden_size=20)
outputs1, hn3 = drnn1(inputs)print(outputs1.shape)  # 包含全部时间步上的隐藏状态
print(hn3.shape)  # 最后一个时间步，隐藏层上50个batch下，20个神经元上的数据
print(outputs1[-1, 0, :])
print(hn3[-1, 0, :])

torch.Size([3, 50, 20])
torch.Size([4, 50, 20])
tensor([-0.2765,  0.4682, -0.0817, -0.2519, -0.1041,  0.0172,  0.2613, -0.0619,-0.2646,  0.0591,  0.1749, -0.1277,  0.3200, -0.3987, -0.2516,  0.1340,-0.3838,  0.2305, -0.2042, -0.2924], grad_fn=<SliceBackward0>)
tensor([-0.2765,  0.4682, -0.0817, -0.2519, -0.1041,  0.0172,  0.2613, -0.0619,-0.2646,  0.0591,  0.1749, -0.1277,  0.3200, -0.3987, -0.2516,  0.1340,-0.3838,  0.2305, -0.2042, -0.2924], grad_fn=<SliceBackward0>)

---

• 使用nn.RNN来实现简单的深度循环神经网，设置输入层为100个神经元，输出层为3个神经元（假设为三分类任务，需要对每个句子预测/进行情感分类），其中每个隐藏层都有256个神经元。

# 对句子层面进行预测，关注最后一个时间步上的输出
import torch
import torch.nn as nnclass myRNN(nn.Module):def __init__(self, input_size=100, hidden_size=256,num_layers=4, output_size=3):super(myRNN, self).__init__()# 四个隐藏层self.rnn = nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)# 输出层self.fc = nn.Linear(hidden_size, output_size)def forward(self, x):output, hn = self.rnn(x)# 关注点 最后一个时间点的输出 从output中索引predict = self.fc(output[-1, :, :])return predictmodel=myRNN()
print(model)

myRNN((rnn): RNN(100, 256, num_layers=4)(fc): Linear(in_features=256, out_features=3, bias=True)
)

# 假设需要对每个单词/每个时间步都进行情感分类
# 对时间步层面进行预测（关注全部时间步上的输出）
import torch
import torch.nn as nnclass myRNN2(nn.Module):def __init__(self, input_size=100, hidden_size=256,num_layers=4, output_size=3):super(myRNN2, self).__init__()# forward需要使用self.hidden_size = hidden_size# 四个隐藏层self.rnn = nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)# 输出层self.fc = nn.Linear(hidden_size, output_size)def forward(self, x):# x 形状  (seq_length, batch_size, input_size)# output 形状 (seq_length, batch_size, hidden_size)output, _ = self.rnn(x)  # _代表hn用不到# 关注点 最后一个时间点的输出 从output中索引output_resize = output.reshape(output.shape[0] * output.shape[1], self.hidden_size)# 假设只关注最后一个时间步的输出predict = self.fc(output_resize[-1, :, :])return predictmodel=myRNN2()
print(model)

myRNN2((rnn): RNN(100, 256, num_layers=4)(fc): Linear(in_features=256, out_features=3, bias=True)
)

# 设置hn的初始化
import torch
import torch.nn as nnclass myRNN3(nn.Module):def __init__(self, input_size=100, hidden_size=256,num_layers=4, output_size=3):super(myRNN3, self).__init__()# 为传入h0 ,定义好需要的属性字段self.num_layers = num_layersself.hidden_size = hidden_size# 四个隐藏层self.rnn = nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)# 输出层self.fc = nn.Linear(hidden_size, output_size)def forward(self, x):# x 形状  (seq_length, batch_size, input_size)# output 形状 (seq_length, batch_size, hidden_size)# 初始化 h0h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size)output, _ = self.rnn(x, h0)  # _代表hn——用不到# 假设只关注最后一个时间步的输出predict = self.fc(output[-1, :, :])return predictmodel=myRNN3()
print(model)

myRNN3((rnn): RNN(100, 256, num_layers=4)(fc): Linear(in_features=256, out_features=3, bias=True)
)

# 实现每个隐藏层上的神经元数量不一致的DRNN
# 前两个隐藏层为256个神经元，后两个隐藏层为512个神经元
import torch
import torch.nn as nnclass myRNN4(nn.Module):def __init__(self, input_size=100, hidden_size=[256, 256, 512, 512],output_size=3):super(myRNN4, self).__init__()# 四个隐藏层self.rnn1 = nn.RNN(input_size=input_size, hidden_size=hidden_size[0])self.rnn2 = nn.RNN(input_size=hidden_size[0], hidden_size=hidden_size[1])self.rnn3 = nn.RNN(input_size=hidden_size[1], hidden_size=hidden_size[2])self.rnn4 = nn.RNN(input_size=hidden_size[2], hidden_size=hidden_size[3])# 输出层self.Linear = nn.Linear(hidden_size[3], output_size)def forward(self, x):# rnn内部执行的是先纵再横的规则——先完成第一个隐藏层上的全部时间步循环，再将全部中间变量传递给第二个隐藏层 依次类推# 先完成每个时间步上的循环，再将该循环信息传递给下一个隐藏层# x 形状  (seq_length, batch_size, input_size)# output 形状 (seq_length, batch_size, hidden_size)# 初始化 h0 对4个隐藏层分别初始化h0 = [torch.zeros(1, x.size(0), self.hidden_size[0]),torch.zeros(1, x.size(0), self.hidden_size[1]),torch.zeros(1, x.size(0), self.hidden_size[2]),torch.zeros(1, x.size(0), self.hidden_size[3])]# 手动实现循环output1, _ = self.rnn(x, h0[0])  # _代表hn——用不到output2, _ = self.rnn(x, h0[1])output3, _ = self.rnn(x, h0[2])output4, _ = self.rnn(x, h0[3])# 取出最后一个batch结果output = self.Linear(output4[-1, :, :])return outputmodel=myRNN4()
print(model)

myRNN4((rnn1): RNN(100, 256)(rnn2): RNN(256, 256)(rnn3): RNN(256, 512)(rnn4): RNN(512, 512)(Linear): Linear(in_features=512, out_features=3, bias=True)
)

4.4 双向循环神经网络

• 双向循环神经网络(Bi-directional RNN，简称BiRNN)：BiRNN是RNN的一种拓展，专门为捕获序列数据中的前后依赖关系而设计。传统的RNN由于结构特点往往只能捕获序列中前向的时序信息，而忽略了后向的上下文，但在文字数据处理过程中，影响一个词语语义的关键信息可能不止在这个词语的前方，也可能在这个词语的后方，而整个句子的含义可能也会因后续的信息发生变化。如：

• “他站在山巅，一眼望去尽是豌蜓的河川和广的森林。“在这个句子中，山巅一词很可能是指一座真正的山峰的山顶。
• “他站在山巅，这个时代之中再也没有人可以与他匹敌。“在这个句子中，山巅一词很可能只是一个比喻，而不是指真正的山峰。

• BiRNN的核心思想是同时在序列的两个方向上运行两个独立的RNN。其中一个RNN按正常顺序处理输入序列，，从第一个词语开始从前向后将词语输入网络；而另一个RNN则从句子的最末端开始，从最后一个词语开始从后向前地将词语输入网络。对于序列中的任意一个时间，BiRNN都可以捕获其前向和后向的信息。这两个方向上的RNN输出，通常会被联结或合并，以形成一个统一的输出表示。
  
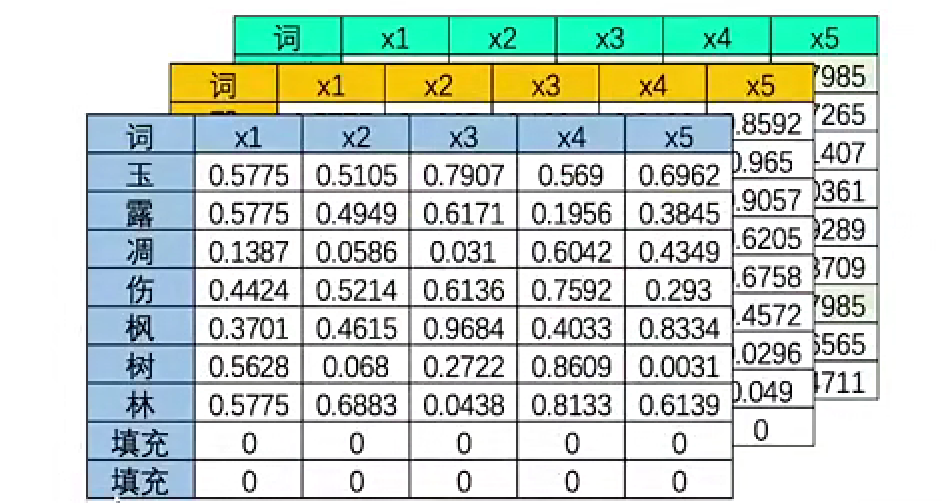
• 双向循环网络的数据流结构：
  
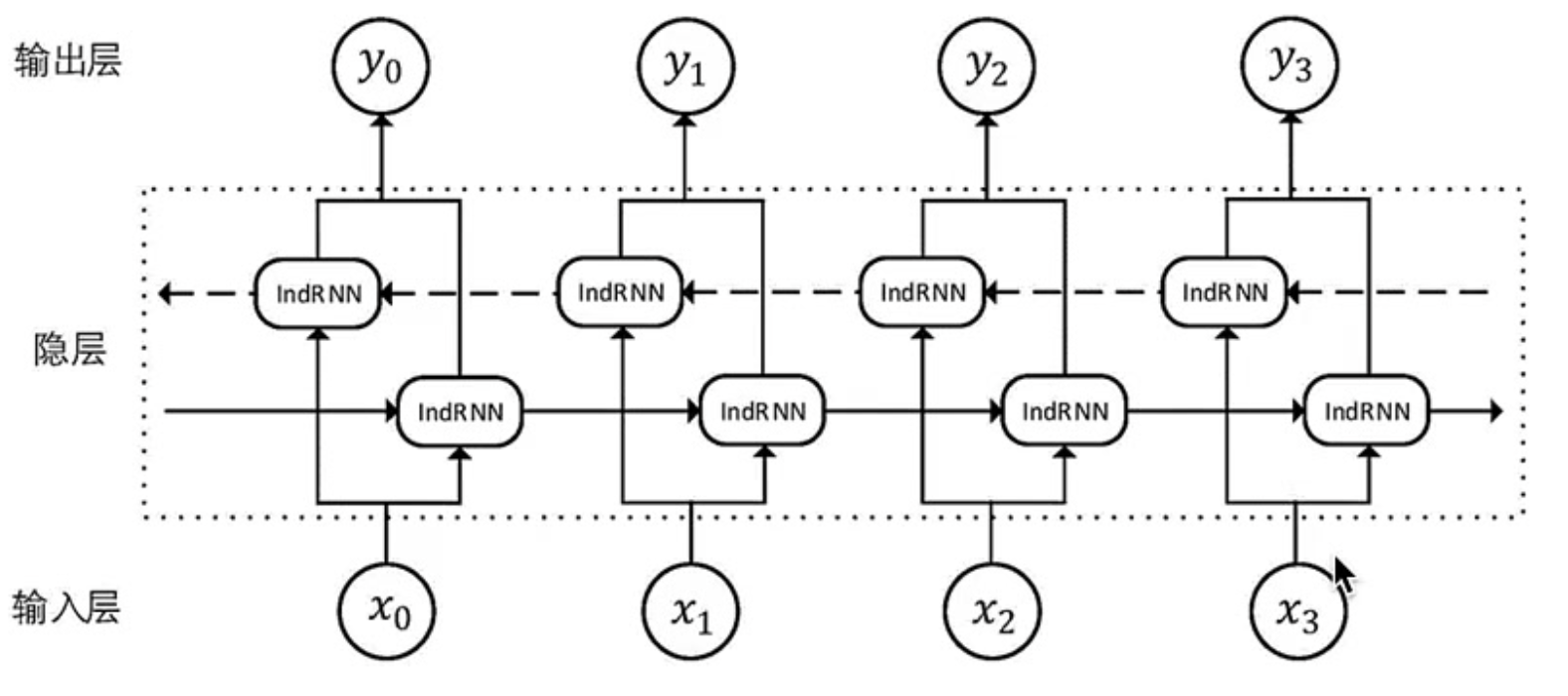
• 在实际代码实现过程中，正向和反向循环是按照顺序进行，没有并行进行处理。理论上，两者是完全独立的，可以并行处理，但为了代码的简洁和效率，双向的RNN按照一定的顺序步骤分步骤执行。一般的执行顺序是先执行正向循环，再执行反向循环。
• 与传统RNN相比，双向RNN的计算需求成倍增加。但双向RNN与其他深度学习结构（如LSTM或GRU）的结合已经显示出卓越的性能，特别是在序列标注、文本分类和机器翻译等任务。
• PyTorch中只需要设置bidirectional为True，即可将传统RNN变为BiRNN。此时，每个隐藏层上，都会有两个独立的RNN数据流。正向数据流从序列的开始到结束进行循环，而反向数据流从序列的结束到开始进行计算。
• 双向RNN的输出维度为$(se{q}_{l}en,batc{h}_{s}ize,2\ast hidde{n}_{s}ize)$，包含正向与反向结果。隐藏状态hn的维度为$(2\ast nu{m}_{l}ayers,batc{h}_{s}ize,hidde{n}_{s}ize)$，分别对应双向层数。

import torch
import torch.nn as nn
input = torch.randn((3, 50, 10))
bi_rnn = nn.RNN(input_size=10, hidden_size=20, bidirectional=True)
outputs4, hn4 = bi_rnn(input)
print(outputs4.shape)  # 对每个时间步、每个batch都生成了双倍的隐藏状态数量
print(hn4.shape) # 隐藏层数量翻倍，隐藏状态数量翻倍

torch.Size([3, 50, 40])
torch.Size([2, 50, 20])

五 RNN的反向传播与缺陷

• 循环神经网络（RNN）凭借其独特结构，能有效捕捉序列数据中的时序依赖关系，在多种序列任务中表现优异。然而，RNN也存在梯度消失、梯度爆炸及长期记忆能力不足等固有缺陷。这些缺陷不仅存在于理论层面，更在实际应用中影响模型性能与训练稳定性。深入理解RNN的局限性，对任务适配及后续改进模型（如LSTM、Transformer）的理解至关重要。

• RNN的局限性与反向传播过程密切相关。反向传播通过链式法则计算损失函数 $L$ 对权重 $W$ 的梯度，并以此更新网络参数，是优化算法（如梯度下降、Adam）实现的关键。RNN的反向传播过程较为复杂，其实际应用中的问题多源于此。

5.1 正向传播的过程

• RNN的数据流包含两个方向：一是沿网络结构的“输入层→隐藏层→输出层”路径，二是沿时间步的“t时刻隐藏层→t+1时刻隐藏层”路径。相应地，其反向传播也分为两个方向：一是常规的“输出层→隐藏层→输入层”路径，二是沿时间反向的“t时刻隐藏层→t-1时刻隐藏层”路径。这种沿时间轴反向传播的机制称为“通过时间的反向传播”（BPTT），是RNN的核心特点。
  
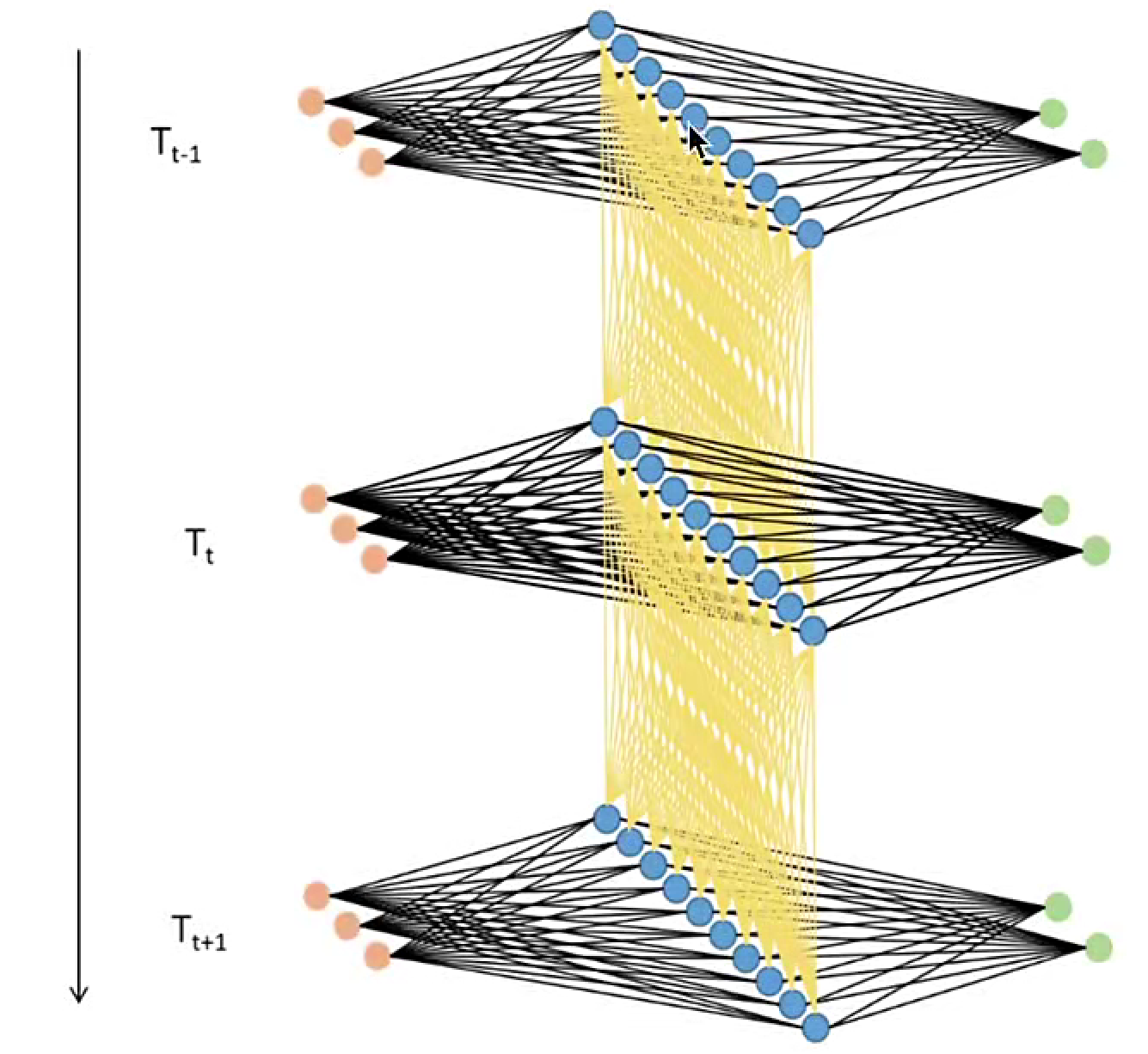
• 通过时间反向传播(BPTT)比一般的反向传播更为复杂，但是它也是从损失函数开始不断向各级的权重$W$求导，并利用导数来迭代求权重的过程。
• 不同NLP任务输出层结构与标签输出方式存在差异。针对词语/样本预测类任务（如情感分类、词性标注等），RNN每个时间步输出对应词语的预测标签；针对句子预测类任务（如生成式任务、seq2seq等），RNN通常仅在最后一个时间步输出句子级预测标签。输出方式的区别会导致反向传播流程的差异，因生成式任务复杂多样，此处以简单的词语分类任务为例讲解RNN反向传播特点与问题。

---

• 假设一个最简RNN用于词语情感分类任务，由输入层、单隐藏层和输出层构成（无截距项），循环$t$个时间步。设输入数据为$X$，预测标签为$\hat{y}$，真实标签为$y$，激活函数为$\sigma$；输入层与隐藏层间权重矩阵为$W_{xh}$，隐藏层与输出层间权重矩阵为$W_{hy}$，隐藏层内部权重矩阵为$W_{hh}$；损失函数为$L(\hat{y},y)$，$t$时刻损失记为$L_t$。此时该RNN的正向传播过程如下：
  
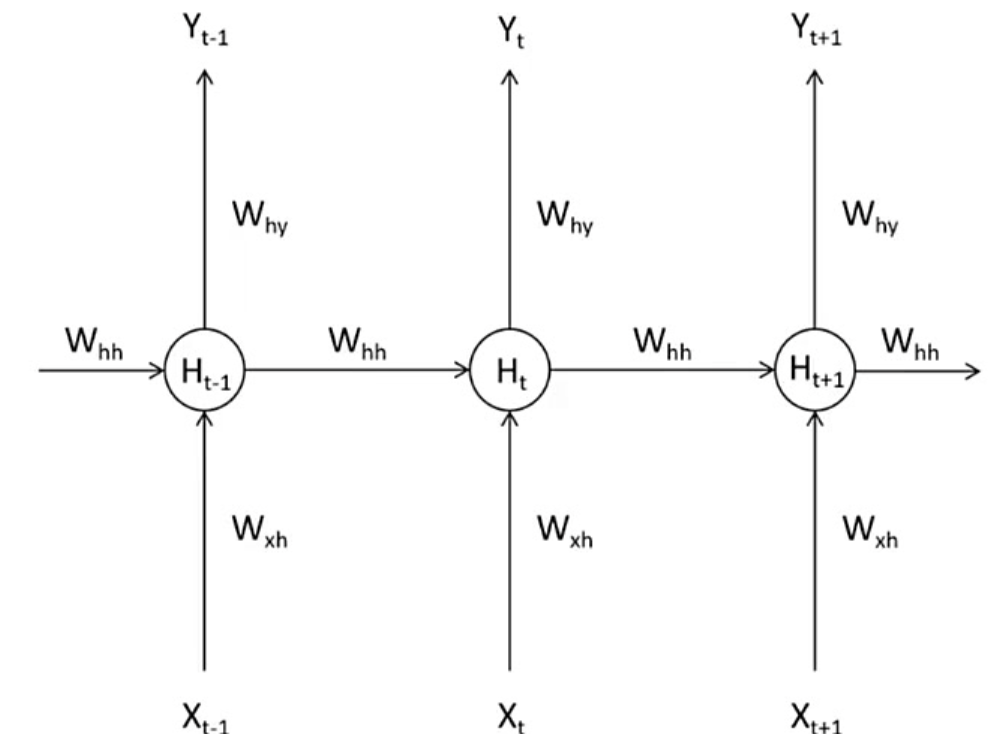
• 在时间步1中，需初始化隐藏状态$h_0$及待迭代参数$W_{hh}$、$W_{xh}$、$W_{hy}$，其正向传播过程的数学表达式为：
  $$\begin{array}{rl}{\mathbf{h}}_1& =\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_1+{\mathbf{W}}_{hh}{\mathbf{h}}_0),\\ {\hat{\mathbf{y}}}_1& ={\mathbf{W}}_{hy}{\mathbf{h}}_1,\\ L_1& =L({\hat{\mathbf{y}}}_1,{\mathbf{y}}_1).\end{array}$$
• 在时间步2中，正向传播过程的数学表达式为：
  $$\begin{array}{rl}{\mathbf{h}}_2& =\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_2+{\mathbf{W}}_{hh}{\mathbf{h}}_1)\\ & =\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_2+{\mathbf{W}}_{hh}\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_1+{\mathbf{W}}_{hh}{\mathbf{h}}_0)),\\ {\hat{\mathbf{y}}}_2& ={\mathbf{W}}_{hy}{\mathbf{h}}_2,\\ L_2& =L({\hat{\mathbf{y}}}_2,{\mathbf{y}}_2).\end{array}$$
• 在时间步$t-1$中，正向传播过程的数学表达式为：
  $$\begin{array}{rl}{\mathbf{h}}_{t-1}& =\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_{t-1}+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-2})\\ & =\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_{t-1}+{\mathbf{W}}_{hh}\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_{t-2}+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-3})),\\ {\hat{\mathbf{y}}}_{t-1}& ={\mathbf{W}}_{hy}{\mathbf{h}}_{t-1},\\ L_{t-1}& =L({\hat{\mathbf{y}}}_{t-1},{\mathbf{y}}_{t-1}).\end{array}$$
• 在时间步$t$中，正向传播过程的数学表达式为：
  $$\begin{array}{rl}{\mathbf{h}}_t& =\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-1})\\ & =\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_t+{\mathbf{W}}_{hh}\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_{t-1}+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-2})),\\ {\hat{\mathbf{y}}}_t& ={\mathbf{W}}_{hy}{\mathbf{h}}_t,\\ L_t& =L({\hat{\mathbf{y}}}_t,{\mathbf{y}}_t).\end{array}$$
• RNN需迭代至少三个权重矩阵：输入层与隐藏层的$W_{xh}$、隐藏层与输出层的$W_{hy}$、隐藏层内部的$W_{hh}$。循环神经网络中，需先完成所有时间步的正向传播，再进行反向传播与参数迭代；计算$h_1$与$h_t$时使用的$W_{xh}$、$W_{hh}$完全相同，这是权值共享的核心——所有表单共享一套参数，本质是各时间步的循环共享同一套参数，无论时间步数量多少，始终使用同一套$W_{hh}$、$W_{xh}$、$W_{hy}$。
  -正向传播完成后，需通过反向传播对输入层与隐藏层（$W_{xh}$）、隐藏层与输出层（$W_{hy}$）、隐藏层内部（$W_{hh}$）这三个权重矩阵求解梯度并迭代更新。反向传播从最后时间步$t$开始，以该时间步为例，需计算的梯度包括：

1. 对$W_{hy}$的梯度：
   $$\frac{\partial L_t}{\partial W_{hy}}=\frac{\partial L_t}{\partial {\hat{\mathbf{y}}}_t}\cdot \frac{\partial {\hat{\mathbf{y}}}_t}{\partial W_{hy}}$$
2. 对$W_{xh}$的梯度：
   $$\frac{\partial L_t}{\partial W_{xh}}=\frac{\partial L_t}{\partial {\hat{\mathbf{y}}}_t}\cdot \frac{\partial {\hat{\mathbf{y}}}_t}{\partial {\mathbf{h}}_t}\cdot \frac{\partial {\mathbf{h}}_t}{\partial W_{xh}}$$
3. 对$W_{hh}$的梯度：
   $$\frac{\partial L_t}{\partial W_{hh}}=\frac{\partial L_t}{\partial {\hat{\mathbf{y}}}_t}\cdot \frac{\partial {\hat{\mathbf{y}}}_t}{\partial {\mathbf{h}}_t}\cdot \frac{\partial {\mathbf{h}}_t}{\partial W_{hh}}$$
   其中，$L_t=L({\hat{\mathbf{y}}}_t,{\mathbf{y}}_t)$且${\hat{\mathbf{y}}}_t=W_{hy}{\mathbf{h}}_t$、${\mathbf{h}}_t=\sigma (W_{xh}{\mathbf{X}}_t+W_{hh}{\mathbf{h}}_{t-1})$，可见$L_t$是复合函数（以${\hat{\mathbf{y}}}_t$为自变量，${\hat{\mathbf{y}}}_t$以$W_{hy}$、${\mathbf{h}}_t$为自变量，${\mathbf{h}}_t$以$W_{xh}$、$W_{hh}$为自变量）。根据链式法则，复合函数求导需逐层传递梯度，上述梯度公式即为链式法则的具体应用。

• RNN反向传播中，由于隐藏状态${\mathbf{h}}_t$依赖前序状态${\mathbf{h}}_{t-1}$（而${\mathbf{h}}_{t-1}$又依赖更早状态），形成嵌套复合函数结构。对$W_{xh}$和$W_{hh}$的梯度需逐层展开：
  • $\frac{\partial L_t}{\partial W_{xh}}$包含两层嵌套：$\frac{\partial L_t}{\partial {\hat{\mathbf{y}}}_t}\cdot \frac{\partial {\hat{\mathbf{y}}}_t}{\partial {\mathbf{h}}_t}\cdot \frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_{t-1}}\cdot \frac{\partial {\mathbf{h}}_{t-1}}{\partial W_{xh}}$；
  • $\frac{\partial L_t}{\partial W_{hh}}$同理，包含$\frac{\partial L_t}{\partial {\hat{\mathbf{y}}}_t}\cdot \frac{\partial {\hat{\mathbf{y}}}_t}{\partial {\mathbf{h}}_t}\cdot \frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_{t-1}}\cdot \frac{\partial {\mathbf{h}}_{t-1}}{\partial W_{hh}}$。

将${\mathbf{h}}_{t-1}$继续拆解至初始状态${\mathbf{h}}_0$，可得到$t$个针对$W_{xh}$和$W_{hh}$的梯度。整个反向传播过程中，每个时间步的梯度数量等于时间步数值（如时间步$t$有$t$个梯度，$t-1$有$t-1$个），总梯度数为算术级数和：
$$\sum _{k=1}^{t}k=\frac{t(t+1)}{2}$$
这些梯度需聚合（如求和或求均值）后用于参数迭代。例如$W_{hh}$的更新规则为：
$$\Delta W_{hh}=\sum _{i=1}^{\frac{t(t+1)}{2}}\frac{\partial L}{\partial W_{hh}^{(i)}},W_{hh}\leftarrow W_{hh}-\eta \cdot \Delta W_{hh}$$
其中$\eta$为学习率。每批数据（batch）处理完毕后执行一次迭代，迭代次数取决于数据集batch数量与训练epoch数。

5.2 RNN反向传播的问题(梯度消失和梯度爆炸)

5.2.1 直观理解

• 在 RNN 中，信息是通过时间步逐步传递的。每一个时间步的隐藏状态都依赖于前一个时间步的隐藏状态，这种依赖关系在反向传播时体现为对同一个权重矩阵（通常是 $W_{hh}$）的反复相乘。
• 想象一下，如果这个权重矩阵的值小于 1，那么每乘一次，梯度就会变得更小一点，经过很多步之后，梯度几乎变成了 0，这就是梯度消失；反之，如果这个值大于 1，每乘一次梯度就会变大，最终变成一个极大的数，这就是梯度爆炸。
• 这种连乘效应在 RNN 中尤其明显，因为时间步可能很长（比如处理一段长文本），导致梯度被反复放大或缩小。

---

5.2.2 数学推导回顾

• 假设损失函数是 $L_t$，它依赖于当前时间步的输出 ${\hat{y}}_t$，而 ${\hat{y}}_t$ 又依赖于当前的隐藏状态 $h_t$，$h_t$ 又依赖于前一个时间步的隐藏状态 $h_{t-1}$，依此类推。
• 当计算损失函数对权重矩阵 $W_{hh}$ 的梯度时，根据链式法则，有：
  $$\frac{\partial L_t}{\partial W_{hh}}=\frac{\partial L_t}{\partial {\hat{y}}_t}\cdot \frac{\partial {\hat{y}}_t}{\partial h_t}\cdot \frac{\partial h_t}{\partial h_{t-1}}\cdots \frac{\partial h_1}{\partial W_{hh}}$$
  其中：
  $$\begin{gathered} \frac{\partial {\hat{y}}_t}{\partial h_t}=W_{hy} \\ \frac{\partial h_k}{\partial h_{k-1}}=W_{hh}（k=2,\dots ,t） \\ \frac{\partial h_1}{\partial W_{hh}}=h_0 \end{gathered}$$
  把这些代入，得到：
  $$\frac{\partial L_t}{\partial W_{hh}}=\frac{\partial L_t}{\partial {\hat{y}}_t}\cdot W_{hy}\cdot (W_{hh}{)}^{t-1}\cdot h_0$$
• 关键在于 $(W_{hh}{)}^{t-1}$ 这一项。如果 $W_{hh}$ 的特征值（可以简单理解为“大小”）小于 1，那么 $(W_{hh}{)}^{t-1}$ 会随着 $t$ 增大而趋近于 0，导致梯度消失；如果大于 1，则会趋近于无穷大，导致梯度爆炸。

---

5.3 梯度消失和梯度爆炸的影响

---

梯度消失

• 表现：模型无法学习到长期依赖关系。因为梯度在反向传播过程中几乎消失，早期时间步的权重几乎得不到更新。
• 后果：RNN 在处理长序列时，往往只能记住最近几步的信息，而无法利用更早的信息。

---

梯度爆炸

• 表现：梯度变得非常大，导致权重更新幅度极大，模型训练不稳定，甚至出现数值溢出（NaN）。
• 后果：训练过程震荡，无法收敛。

---

• 为什么 RNN 比一般深度网络更容易出现梯度消失？

• 在普通的前馈神经网络中，梯度消失也可能发生，但 RNN 更加严重，因为：RNN 的反向传播是在时间维度上进行的，相当于一个“非常深”的网络，时间步越多，网络越深。同一个权重矩阵 $W_{hh}$ 在每一时间步都被反复使用，导致梯度连乘效应更加显著。

---

5.4 缓解梯度消失和梯度爆炸的方法

5.4.1 梯度裁剪（Gradient Clipping）

• 适用场景：主要用于缓解梯度爆炸。
• 做法：当梯度的模超过某个阈值时，按比例缩小梯度，使其不超过阈值。
• 公式：
  $$\text{if }\Vert g\Vert >\text{threshold},g\leftarrow \frac{\text{threshold}}{\Vert g\Vert }\cdot g$$

5.4.2 改进的 RNN 结构（如 LSTM、GRU）

• 适用场景：主要用于缓解梯度消失。
• LSTM（Long Short-Term Memory）：通过引入“门控机制”（输入门、遗忘门、输出门）和“细胞状态”，使得网络可以选择性地记忆或遗忘信息，从而有效缓解梯度消失。
• GRU（Gated Recurrent Unit）：LSTM 的简化版本，同样通过门控机制控制信息流动。

5.4.3 合理的权重初始化

• 使用如 Xavier 或 He 初始化等方法，使得初始权重既不会太大也不会太小，从而在一定程度上缓解梯度消失和爆炸。

5.5 RNN的其他问题

RNN 存在三方面运算缺陷：

1. 运算复杂度高、效率低：RNN 需逐时间步循环执行递归运算，下一个时间步需等待前一时间步完成，难以适配多核、并行等技术加速，长序列处理时顺序计算量大，效率低下。
2. 内存利用率低：反向传播需存储每个时间步中间状态，长序列内存开销大，反向传播计算量也大，进一步加剧长序列运算负担。
3. 参数规模庞大：采用全链接层且叠加循环维度，使整体参数量显著增加，即便限制参数数量，规模仍较大。
4. 过拟合风险高：参数量巨大但学习能力不足，且无正则化层（如 normalization 层、dropout 层）约束过拟合；循环结构下正则化层应用难度大，进一步加剧过拟合控制难度。

5.6 小结

• RNN 的梯度消失和梯度爆炸主要源于反向传播中权重矩阵的连乘效应。
• 梯度消失导致模型无法学习长期依赖，梯度爆炸导致训练不稳定。
• RNN 比一般深度网络更容易出现这些问题，因为时间步相当于“深度”，且同一权重被反复使用。
• 常见的缓解方法包括梯度裁剪、使用 LSTM/GRU、合理的权重初始化等。