Scikit-learn Python机器学习 - 回归分析算法 - 岭回归 (Ridge Regression)
锋哥原创的Scikit-learn Python机器学习视频教程:
https://www.bilibili.com/video/BV11reUzEEPH
课程介绍

本课程主要讲解基于Scikit-learn的Python机器学习知识,包括机器学习概述,特征工程(数据集,特征抽取,特征预处理,特征降维等),分类算法(K-临近算法,朴素贝叶斯算法,决策树等),回归与聚类算法(线性回归,欠拟合,逻辑回归与二分类,K-means算法)等。
Scikit-learn Python机器学习 - 回归分析算法 - 岭回归 (Ridge Regression)
前面学的线性回归有个问题,就是会出现过拟合问题。所以我们建议使用更高级的基于L2正则化的线性回归,也就是今天我们要学习的岭回归。
过拟合和欠拟合
过拟合和欠拟合是机器学习中常见的两种模型问题,它们分别表示模型在学习过程中的两种极端情况。
-
过拟合(Overfitting):
-
定义:过拟合是指模型在训练数据上表现得非常好,甚至可以完美地拟合训练数据,但在新数据(测试数据)上的表现却很差。也就是说,模型过于复杂,捕捉到了训练数据中的噪声或偶然性,导致其在真实数据上没有泛化能力。
-
原因:通常是因为模型太复杂,参数过多,训练时没有足够的正则化,或者训练数据量不足,导致模型记住了训练数据中的细节和噪声。
-
表现:训练误差很小,但测试误差很大。
-
解决办法
-
降低模型的复杂度(例如,减少特征数量、使用更简单的模型)。
-
使用正则化技术(例如,L1或L2正则化)。
-
增加更多的训练数据。
-
使用交叉验证来优化模型。
-
-
-
欠拟合(Underfitting):
-
定义:欠拟合是指模型过于简单,无法捕捉数据中的潜在模式或关系,导致在训练数据和测试数据上都表现不佳。
-
原因:模型过于简单,缺少足够的参数或复杂性来学习数据中的模式,或者训练过程中没有进行充分的训练。
-
表现:训练误差和测试误差都很高。
-
解决办法
-
增加模型的复杂度(例如,使用更复杂的模型或更多的特征)。
-
训练更多的周期,优化模型的参数。
-
调整超参数,使模型能更好地拟合数据。
-
-
总结:
-
过拟合:模型太复杂,过于关注训练数据中的噪声,导致无法泛化。
-
欠拟合:模型太简单,无法捕捉数据中的重要规律,导致学习不足。
理想的模型应当是在训练数据和测试数据之间达到一个平衡,既不对训练数据过于依赖(过拟合),也不遗漏数据中的关键特征(欠拟合)。
L2 正则化
L2 正则化(也称为 岭回归 或 权重衰减)是一种常用的正则化技术,用来避免机器学习模型中的过拟合问题。它通过在损失函数中添加一个惩罚项(即正则化项)来限制模型的复杂度,从而避免模型过度拟合训练数据。
数学原理
L2 正则化的核心思想是惩罚模型中参数(权重)过大。具体地,它通过在损失函数中添加一个关于权重的平方和作为正则化项来控制模型复杂度。假设我们有一个线性回归模型,损失函数包含两部分:
-
预测误差(例如均方误差,MSE):度量模型对训练数据的拟合程度。
-
正则化项(L2 正则化项):控制模型的复杂度。
线性回归中的L2正则化
在普通的线性回归模型中,损失函数为:

在应用 L2 正则化 后,损失函数变为:

L2 正则化项的作用:
-
惩罚大权重:通过对权重的平方和进行惩罚,L2 正则化会让模型更倾向于减小权重的值,尤其是较大的权重。这可以防止模型过于依赖某些特征,从而更好地泛化到新数据。
-
平滑模型:L2 正则化鼓励权重向零收敛,但不会像L1正则化那样将权重变成零。因此,L2 正则化通常会导致较小但非零的权重值,从而使模型更加平滑和稳定。
L2 正则化的优化过程
在梯度下降优化中,我们需要对损失函数进行最小化。在添加了L2正则化项后,损失函数的梯度变为:
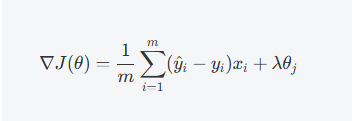
这里,第一项是普通的损失函数的梯度,而第二项是正则化项对每个参数的梯度影响。通过梯度下降更新参数时,L2 正则化会使得每个权重的更新不仅依赖于数据的误差,还会受到其自身的大小的影响。这意味着:
-
大权重会被更强地惩罚,使得它们在训练过程中逐渐减小。
-
小权重的更新会较小,因此可以保持其重要性。
API介绍
Ridge 类是 scikit-learn 中实现岭回归的核心类,位于 sklearn.linear_model 模块中。
Ridge(alpha=1.0, *, fit_intercept=True, copy_X=True, max_iter=None, tol=0.001, solver='auto', positive=False, random_state=None)参数详解:
1. alpha (正则化强度)
-
类型: float, 默认为 1.0
-
作用: 控制正则化的强度,必须是正浮点数
-
影响:
-
α 值越大,正则化效果越强,系数收缩越明显
-
α = 0 时退化为普通线性回归
-
α → ∞ 时所有系数趋近于 0
# 不同 alpha 值的示例 ridge_weak = Ridge(alpha=0.1) # 弱正则化 ridge_medium = Ridge(alpha=1.0) # 中等正则化(默认) ridge_strong = Ridge(alpha=10.0) # 强正则化 -
2. fit_intercept (是否计算截距)
-
类型: bool, 默认为 True
-
作用: 指定是否计算模型的截距项
-
建议: 通常保持为 True,除非数据已经中心化
3. copy_X (是否复制数据)
-
类型: bool, 默认为 True
-
作用: 如果为 True,会复制 X;否则可能被覆盖
-
建议: 通常保持默认值 True
4. max_iter (最大迭代次数)
-
类型: int, 默认为 None
-
作用: 对于迭代求解器,设置最大迭代次数
-
适用求解器: 'sag', 'saga', 'lsqr'
5. tol (优化精度)
-
类型: float, 默认为 0.001
-
作用: 优化的精度,用于判断收敛的条件
-
适用求解器: 'sag', 'saga', 'sparse_cg', 'lsqr'
6. solver (求解器选择)
-
类型: str, 默认为 'auto'
-
可选值:
-
'auto': 自动选择
-
'svd': 使用奇异值分解
-
'cholesky': 使用标准 scipy.linalg.solve 函数
-
'lsqr': 最小二乘迭代方法
-
'sparse_cg': 共轭梯度法,适用于稀疏矩阵
-
'sag': 随机平均梯度下降
-
'saga': 'sag' 的改进版本
-
'lbfgs': 适用于强制正系数的情况
-
7. positive (强制正系数)
-
类型: bool, 默认为 False
-
作用: 当设置为 True 时,强制系数为非负数
-
限制: 仅支持 'lbfgs' 求解器
8. random_state (随机种子)
-
类型: int, 默认为 None
-
作用: 当 solver 为 'sag' 或 'saga' 时,用于打乱数据的随机种子
-
用途: 确保结果可重现
不同求解器的适用场景
| 求解器 | 适用场景 | 特点 |
|---|---|---|
| auto | 默认选择 | 根据数据自动选择最佳求解器 |
| svd | 稳定性要求高 | 数值稳定性好,适合特征多的情况 |
| cholesky | 标准场景 | 封闭解,效率高 |
| sparse_cg | 稀疏数据 | 适合大规模稀疏矩阵 |
| lsqr | 大规模数据 | 迭代方法,内存效率高 |
| sag | 超大样本量 | 随机梯度下降变种,速度快 |
| saga | 超大样本量 | sag的改进版本,支持更多正则化 |
| lbfgs | 强制正系数 | 唯一支持positive=True的求解器 |
具体示例-加州房价预测
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import SGDRegressor, Ridge
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 1,加载数据
california = fetch_california_housing()
print(california.data, california.data.shape)
print(california.target)
print(california.feature_names)
# 2,数据预处理
X_train, X_test, y_train, y_test = train_test_split(california.data, california.target, test_size=0.2, random_state=20)
scaler = StandardScaler() # 数据标准化:消除不同特征量纲的影响
X_train_scaled = scaler.fit_transform(X_train) # fit计算生成模型,transform通过模型转换数据
X_test_scaled = scaler.transform(X_test) # # 使用训练集的参数转换测试集
# 3,创建和训练岭回归模型(梯度下降)
ri_model = Ridge() # 创建分类器实例
ri_model.fit(X_train_scaled, y_train) # 训练模型
print('权重系数:', ri_model.coef_)
print('偏置值:', ri_model.intercept_)
# 4,模型评估
y_predict = ri_model.predict(X_test_scaled)
print('预测值:', y_predict)
mse = mean_squared_error(y_test, y_predict)
print('梯度下降方程-均方误差:', mse)运行结果:
[[ 8.3252 41. 6.98412698 ... 2.5555555637.88 -122.23 ][ 8.3014 21. 6.23813708 ... 2.1098418337.86 -122.22 ][ 7.2574 52. 8.28813559 ... 2.8022598937.85 -122.24 ]...[ 1.7 17. 5.20554273 ... 2.325635139.43 -121.22 ][ 1.8672 18. 5.32951289 ... 2.1232091739.43 -121.32 ][ 2.3886 16. 5.25471698 ... 2.6169811339.37 -121.24 ]] (20640, 8)
[4.526 3.585 3.521 ... 0.923 0.847 0.894]
['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude']
权重系数: [ 0.83271955 0.11746627 -0.2758307 0.29880521 -0.00792198 -0.03964163-0.88166375 -0.85262095]
偏置值: 2.0678235537788865
预测值: [1.58303122 3.01531685 1.75389447 ... 1.84162164 2.81022657 1.16703968]
梯度下降方程-均方误差: 0.5410161998327475