Leecode hot100 - 105.从前序与中序遍历序列构造二叉树
题目描述
https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/description/?envType=problem-list-v2&envId=2cktkvj
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
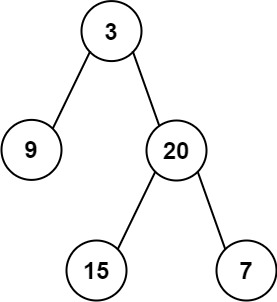
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1] 输出: [-1]
思路
-
前序定根,中序分左右,递归建子树
-
前序遍历的顺序是:根节点 → 左子树 → 右子树
-
中序遍历的顺序是:左子树 → 根节点 → 右子树
-
-
因此,前序遍历的第一个元素是根节点,而这个根节点在中序遍历中会将序列分为左子树和右子树两部分
-
通过哈希表快速定位根节点在中序遍历中的位置,根节点左侧的所有元素构成左子树的中序遍历,右侧构成右子树的中序遍历。
-
根据中序遍历中左子树的元素数量(根节点索引 - 中序左边界),在前序遍历中划分出左子树和右子树的范围
-
递归构建子树
代码
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
# 创建中序遍历值到索引的映射,用于快速查找根节点位置
index = {val: idx for idx, val in enumerate(inorder)}
# 递归函数:根据指定范围的前序和中序遍历构建子树(范围是左闭右开区间)
def dfs(pre_left: int, pre_right: int, in_left: int, in_right: int) -> Optional[TreeNode]:
# 递归终止条件:如果左边界等于右边界,说明当前范围内没有节点
if pre_left == pre_right:
return None
# 前序遍历的第一个元素是当前子树的根节点
root_val = preorder[pre_left]
# 创建当前根节点
root = TreeNode(root_val)
# 找到根节点在中序遍历中的位置
root_idx = index[root_val]
# 计算左子树的节点数量
left_size = root_idx - in_left
# 递归构建左子树
# 左子树在前序中的范围:[pre_left+1, pre_left+1+left_size)
# 左子树在中序中的范围:[in_left, root_idx)
root.left = dfs(pre_left + 1, pre_left + 1 + left_size, in_left, root_idx)
# 递归构建右子树
# 右子树在前序中的范围:[pre_left+1+left_size, pre_right)
# 右子树在中序中的范围:[root_idx+1, in_right)
root.right = dfs(pre_left + 1 + left_size, pre_right, root_idx + 1, in_right)
return root
# 初始调用递归函数,处理整个遍历序列(左闭右开区间)
return dfs(0, len(preorder), 0, len(inorder))
复杂度分析
-
时间复杂度:O(n),其中 n 为 preorder 的长度。递归 O(n) 次,每次只需要 O(1) 的时间。
-
空间复杂度:O(n)。哈希表
