当前位置：首页 > news >正文

【读论文】压缩双梳光谱技术

news 2025/9/23 8:07:06

丹尼尔・I・赫尔曼 ¹*、马修・沃尔什 ²、莫莉・凯特・克赖德 ¹、³、诺亚・洛迪 ³、尤金・J・曹 ¹、亚历山大・J・林德 ¹、马修・海里奇 ¹、³、约书亚・库姆斯 ¹、热罗姆・热内斯特 ²*、斯科特・A・迪达姆 ¹、³*¹ 美国科罗拉多州博尔德市科罗拉多大学博尔德分校电气、计算机与能源工程系；² 加拿大魁北克省拉瓦尔大学光学、光子学与激光中心；³ 美国科罗拉多州博尔德市科罗拉多大学博尔德分校物理系* 通讯作者：电子邮箱：daniel.i.herman@colorado.edu（D.I.H.）；jgenest@gel.ulaval.ca（J.G.）；scott.diddams@colorado.edu（S.A.D.）
赫尔曼等，《科学》，387，653-658（2025），2025 年 2 月 7 日

研究背景

光学频率梳（OFC）为宽带、高分辨率光谱学和精密干涉测量技术带来了显著优势。然而，量子力学最终限制了激光频率梳可实现的计量精度。量子压缩技术已借助连续波激光器大幅提升了测量性能，但利用压缩梳实现计量优势的实验研究仍有待深入。本研究利用非线性光纤中的克尔效应，对中心波长为 1560 纳米、频率为 1 吉赫兹的频率梳进行幅度压缩，在 2.5 太赫兹带宽内实现了超过 3 分贝（dB）的压缩效果。双梳干涉测量技术对硫化氢气体进行模式分辨光谱分析，其信噪比突破散粒噪声极限近 3 分贝。量子噪声的降低使得气体浓度测定的量子速度提升两倍，这一成果对动态化学环境中多种物质的高速测量具有重要意义。

过去 25 年，光学频率梳（OFC）的发展彻底改变了对时间、频率和距离等物理量的测量方式（1）。可溯源、相位相干且具备宽带特性的光学频率梳被广泛应用于原子与分子光谱学研究。作为一种覆盖太赫兹至紫外波段的活性光源，光学频率梳拓展了基础光谱学与应用光谱学的技术前沿（2, 3），其应用领域涵盖生物与化学传感（4）以及量子系统的高分辨率测量（5）。随着基于频率梳的应用日益重要，深入理解并降低这些独特测量工具所面临的基本量子噪声限制，已成为亟待解决的关键问题。

近期，光学频率梳计量技术已达到相干态所决定的量子散粒噪声极限（SNL）（图 1，A 和 B）（6-8）。若要进一步突破该极限以提升光谱灵敏度，可引入压缩态，这一方法此前已在连续波激光器中成功应用（9）。目前已有多项关于将压缩光学频率梳用作光谱工具的提议（10, 11），其中可实现的压缩水平（约 10 分贝）有望在实用功率水平（微瓦至毫瓦级）下带来显著的量子优势。与此同时，利用光学参量振荡器、微谐振器光学频率梳及其他平台生成量子光学频率梳的研究也取得了重大进展（12-14）。这些进展与将量子光学频率梳用作量子计算（15）和时间测量（16）量子资源的研究同步推进。然而，在光谱学这一光学频率梳最重要的应用领域中，尚未有实验证明压缩光学频率梳可带来计量优势。

本文提出了一种生成高亮度幅度压缩 1 吉赫兹光学频率梳的简便方案，并将其应用于分子样品的模式分辨双梳光谱（DCS）研究。现有量子增强型光学频率梳光谱方案均利用光学非线性对少数梳模进行压缩（10, 11）。尽管通过 χ⁽²⁾非线性可在较宽光学带宽内实现压缩（17），但本研究选择更易获取的 χ⁽³⁾非线性，在 2.5 太赫兹宽的光学带宽内，对超过 2500 个梳模的幅度测量量子噪声进行抑制。本实验装置以成熟的孤子压缩技术（18-20）为基础，同时融合了最新的干涉相位测量方法（21）。研究表明，即便仅对两个光学频率梳中的一个进行压缩，高亮度幅度压缩仍能为宽带共线双梳光谱技术带来计量优势。在样品探测前将两个光学频率梳重叠，可实现基线校准传输测量，从而充分发挥量子压缩的优势。该技术为量子增强型双梳光谱技术的实际应用场景开发奠定了基础。

双梳光谱中的量子噪声

双梳光谱技术无需机械延迟线或衍射光学元件，即可在太赫兹光学带宽内实现具有梳模分辨率的可溯源光谱测量（3）。在双梳光谱技术中，将两个模式间距不同的频率梳进行干涉，可将光学梳光谱和吸收信息下转换至射频（RF）域，在此域内对信号进行记录，并以绝对频率标度为基准进行校准（图 1B）。在频域中，双梳干涉表现为多外差射频梳，而时域波形则呈现为周期性干涉图。分子吸收信息既以射频梳光谱中的凹陷形式呈现，也以干涉图后的自由感应衰减（FID）信号形式体现。双梳光谱技术推动了电磁光谱范围内宽带、高分辨率、可溯源传感技术的发展，其应用包括开放光路环境传感（22）、化学反应监测（4）、化学成像（23）以及为广泛分布的数据库生成精确的存档光谱（24）。

通过降低技术噪声源（如梳的相对强度噪声、探测器噪声和热噪声），相干态的基本量子散粒噪声成为梳模幅度测量中的主要不确定因素（图 1B）（25, 26）。假设噪声过程具有时间平稳性，1 赫兹带宽内受散粒噪声限制的光电流波动可表示为 σₛₙₗ=√(2e iₐᵥ₉)，其中 e 为基本电荷，iₐᵥ₉为平均光电流（27）。我们将这一极限称为时间平稳散粒噪声极限。在某些情况下，可利用光电流噪声的循环平稳脉冲特性（28, 29），或引入双梳干涉图的更高频率 “副本”（6），从而在梳测量中突破该散粒噪声极限。与之不同的是，本研究通过利用光的量子态，突破了双梳光谱技术中的时间平稳散粒噪声极限。此外，量子增强技术还应能突破循环平稳极限。

我们提出的量子增强方法解决了以往理论方法未能充分涵盖的双梳测量特性问题。在时域中，干涉图可分解为两个区域：零光程差（中心脉冲）区域和大光程差区域。在中心脉冲区域，两个光学频率梳的光脉冲在时间上重叠，测量实现模式匹配（图 2A 和 B）。中心脉冲包含两个光学频率梳的光谱包络信息，而分子或原子气体的吸收则以自由感应衰减信号的形式呈现，且该信号在时间上与中心脉冲基本分离（3）。

从量子光学角度来看（图 2C），经典中心脉冲是由第一个光学频率梳的相干态与第二个光学频率梳的模式匹配相干态通过分束器相互作用产生的，从而形成 “类正交” 测量（30）。在此过程中，通过零差或外差比较可获取梳场的相位和幅度噪声正交分量，在强本地振荡梳极限下，可实现纯正交测量（31）。在大光程差情况下，两个脉冲序列在时间上分离。该区域可通过任一光学频率梳的相干态与真空态的分束器相互作用来建模，从而形成 “类强度” 测量（30）。因此，对于大光程差而言，无论梳功率比如何，噪声均源自独立光学频率梳的散粒噪声。实验中使用的 1 吉赫兹光学频率梳的占空比（脉冲长度与脉冲重复周期的比值）约为 0.025%，因此双梳光谱的量子噪声主要由类强度测量噪声决定。

对于自由感应衰减信号，若吸收深度较小且相应的自由感应衰减信号振荡较弱，则其噪声仍主要由类强度测量的散粒噪声决定。同样，由于长持续时间、窄带宽的自由感应衰减脉冲与短持续时间、宽带宽的采样梳脉冲之间存在模式失配，可将自由感应衰减信号近似视为真空态。这一解释与传统傅里叶变换光谱（FTS）的分析结果一致。与可调谐激光光谱技术相比，傅里叶变换光谱技术（包括双梳光谱技术）会因未与吸收介质相互作用的光子产生散粒噪声，而导致噪声 penalty（32）。本研究中，基于小吸收深度和低损耗的假设，利用高亮度幅度压缩光学频率梳降低大光程差区域的散粒噪声，从而为双梳光谱技术带来优势，这与之前的分析结果一致（10）。尽管幅度压缩会给探测到的自由感应衰减信号增加相位噪声，但共线探测对自由感应衰减信号的幅度敏感，因此吸收测量不会因这种附加噪声而产生偏差。对中心脉冲区域进行全面的量子分析，有望将量子增强型双梳干涉技术拓展至测距和时间传递等其他应用领域。

单梳压缩

压缩双梳光谱仪的简化示意图如图 3A 所示 [详见（33）]。两个光学频率梳由两台重复频率为 1 吉赫兹的飞秒激光器产生（4），发射中心波长为 1563 纳米的孤子脉冲（图 3B）。将两个光学频率梳相位锁定到共同的光学基准上，以确保它们之间的相干性。其中一个光学频率梳被压缩至 260 飞秒，并按照 10:1 的功率比分为强脉冲（平均功率 24 毫瓦）和弱辅助脉冲。这些脉冲被耦合到 χ⁽³⁾非线性光纤的正交偏振轴上，由于克尔效应，强脉冲会经历与强度相关的相移。在相空间中，这一过程将相干态的不确定性转变为月牙形的压缩噪声分布（图 3C）。由于克尔效应守恒光子数，压缩角的调整使得对未位移克尔态的强度噪声测量结果与输入相干态的测量结果（即时间平稳散粒噪声极限）相同（20）。通过轻微位移克尔态，可改变压缩角，从而在强度测量中观察到量子噪声降低（QNR）或量子噪声放大现象。这种轻微位移是通过在可变分束器上，将强压缩态脉冲与弱辅助相干态脉冲（已施加可调相移）按照 100:1 的功率比重新组合实现的。

当相对相位约为 90° 或 270° 时，位移后的态与原始克尔态具有相同的平均场幅度，但幅度正交分量的方差会出现可观测的压缩或反压缩现象（图 3D）。我们使用一台高量子效率（η=93%）的光电探测器对克尔态的压缩特性进行表征（图 S1）。通过在不同光功率水平下记录校准曲线，验证了光学频率梳的散粒噪声限制特性（图 S2）。借助辅助脉冲，在 45 兆赫兹附近测量到了高达 3.8 分贝的压缩和 4.0 分贝的反压缩，并在 10 兆赫兹至 100 兆赫兹的更宽频段内测量到了超过 3 分贝的压缩（图 3E）。当 14.7 毫瓦的克尔态与约 150 毫瓦的辅助脉冲（经耦合损耗后）重新组合时，测量到的压缩效果最佳，这一结果与之前的测量结果相当（20）。若没有辅助脉冲，测得的强度噪声与同等功率的相干态光学频率梳的强度噪声一致，这与预期相符。我们还使用另一台量子效率 η=70% 的高速探测器，在 20 兆赫兹至 500 兆赫兹频段内测量到了约 2 分贝的压缩（图 S3）。

通常，量子传感应用要么利用宽带低频压缩 [例如激光干涉引力波天文台（LIGO）]，要么利用窄带高频压缩（34, 35）。尽管宽带高频压缩已被用于量子信息处理（36），但本研究结果表明，双梳光谱技术是高亮度宽带压缩的另一个重要应用领域。例如，当重复频率差为 5 千赫兹时，500 兆赫兹的电带宽可支持超过 90 太赫兹的量子增强型双梳光谱测量。

共线量子增强型双梳光谱技术

双梳光谱技术的时域图像表明，高亮度压缩态可用于量子增强。然而，我们需要确定哪些双梳几何结构与高亮度幅度压缩态的使用兼容。最近，有研究提出了一种量子增强型双梳光谱方案，该方案在吸收体位于分束器前的一个光学频率梳光路上（即非对称双梳光谱），实现了梳模与其边带之间的双模压缩（3, 10）。但这种双模压缩方案需要使用定制组件，实施难度较大。

作为替代方案，我们采用了一种更简便的方法：将一个光学频率梳制备为高亮度单模幅度压缩态，该压缩态通过上述成熟且简单的技术生成（20）。将压缩光学频率梳与相干态光学频率梳在分束器上混合后，输出的干涉图将具有相反的符号，且量子噪声会部分反相关。非对称双梳光谱的最佳测量策略是平衡光电探测，但这种光电流减法方法在最大化双梳光谱信号的同时，会消除压缩带来的优势。

因此，我们采用共线双梳光谱方案，将混合后的光学频率梳通过吸收体（图 S4）。在该方案中，吸收信号被记录在一个干涉图上，而另一个干涉图则作为光谱基线参考。对两个干涉图进行傅里叶变换，可得到复光谱，将其相除即可得到分子透射率的增强估计值（推导过程详见补充材料）。重要的是，由于傅里叶变换的线性特性，压缩在时域中产生的相关性会在频域中保持。此外，在高信噪比和低吸收率的极限条件下，光谱除法对反相关噪声的处理方式类似于时域光电流加法，而时域光电流加法是表征幅度压缩态的标准方法（37, 38）。我们对两个干涉图分别进行数字后处理，以便于比较时域加法和光谱除法两种方法。将两个光电流相加，可抵消符号相反的干涉图，这与双梳光谱技术中用于背景抑制的光学方法类似（39）。同时，由于噪声呈反相关，光电流加法也能部分抵消噪声。

在实验中，我们生成了幅度压缩光学频率梳（约 15 毫瓦）与弱相干态光学频率梳（约 10 毫瓦）之间的干涉图。尽管两者功率不平衡，但双梳光谱数据的品质因数仍达到了当前最先进水平（>10⁷赫兹 ^(-1/2)）（3）。我们将光学锁定频率设置为使干涉图中心位于 50 兆赫兹。当重复频率差为 5.6 千赫兹时，双梳光谱覆盖的射频带宽约为 25 兆赫兹。两个中心脉冲除了存在 180° 的相位差外，其余特性完全匹配（图 4A）。在初步分析中，通过互相关对原始干涉图进行时间对齐，然后求和（图 4B 和 C）。随后，对无辅助脉冲（散粒噪声极限）、压缩（SQZ）和反压缩（ANTI-SQZ）三种情况下中心脉冲之外区域的量子噪声进行分析。原始时域量子噪声降低量为 55%（2.6 分贝）。若考虑高速数字化仪的电噪声本底，压缩水平可达 3.5 分贝。无论是在无辅助脉冲情况下将光电流相加，还是对压缩光电流进行减法运算，所得到的散粒噪声极限结果相似，均能观察到类似的量子噪声降低。这些结果既验证了单梳压缩测量的有效性，也表明压缩效应可推广到双梳体系中。

频域双梳光谱结果

要利用量子增强型双梳系统测量梳模分辨光谱，需要对干涉图进行相位校正（图 S5），以消除梳的相位和时序波动（40, 41）。对每个通道的相位校正干涉图序列进行模式分辨光谱分析，均可观察到压缩信号（图 S6）。接下来，将相位校正后的干涉图进行叠加，为每个通道生成一个高信噪比干涉图。对每个通道的干涉图进行互相关相位对齐、傅里叶变换（FFT）和除法运算，得到透射光谱，从而完全展现量子噪声降低效果。利用倒频谱域滤波对剩余的光谱基线变化进行校正，该方法可同时消除极高光程差下的标准具和噪声（42）。我们采用非线性最小二乘回归方法，将透射率与 HITRAN2020 模型（24）进行拟合，以压力、温度和光程长度为输入参数，提取数密度。拟合覆盖了中心波长为 1563 纳米、带宽为 20 纳米的范围，包含了 67 个光谱线强度高于 10^(-23) 厘米 ^(-1)/（分子 × 厘米 ^(-2)）的硫化氢（H₂S）振转跃迁（图 5A 和 B）。样品池的低压（100 托）环境使得谱线宽度约为 1 吉赫兹，因此每个吸收特征仅由少数几个梳模采样（图 5C）。尽管如此，我们的数据仍与模型高度吻合，在不到 10 毫秒的平均时间内，残差处于亚百分比水平，这验证了我们处理算法的性能。

对拟合残差的进一步分析表明，在三种实验条件（散粒噪声极限、压缩和反压缩）下，残差均按 1/√Nᵢ的规律变化，其中 Nᵢ为平均干涉图的数量（图 S7）。对三种条件分别进行幂律拟合，结果显示噪声随平均次数的增加而降低。压缩或反压缩会改变幂律的常数因子（9）。压缩与散粒噪声极限情况下的常数因子比值为 0.51，表明功率信噪比提升了 2.9 分贝（相当于量子速度提升两倍），这与原始时域数据中观察到的结果几乎一致。

在频域中也观察到了类似的量子噪声降低现象，表现为残差随双梳功率的变化（图 S8）。值得注意的是，压缩并未对拟合结果产生偏差，且拟合精度的提升与时域和频域中的量子噪声降低量相符。具体而言，反压缩、散粒噪声极限和压缩情况下的拟合数密度分别为 5.197±0.150 摩尔 / 立方米、5.427±0.098 摩尔 / 立方米和 5.382±0.072 摩尔 / 立方米，这表明压缩降低了浓度测定的不确定性。所有拟合值均与样品池制造商提供的数密度（5.454 摩尔 / 立方米，对应 294 开尔文下 100 托）在统计上一致。在当前数据集中，我们无法确定在分子吸收较高的区域压缩效果是否会减弱（图 S9）。

最后需要说明的是，所展示的共线双梳光谱技术的分辨率极限约为 50 兆赫兹。该极限由光学模式频率间隔决定，而非非对称双梳光谱中假设的梳模线宽。通过对两组频率下的光谱采样效应进行建模，有望进一步提高分辨率。这一分辨率水平足以满足包括大气光谱学（22）在内的众多应用需求。

讨论与展望

本研究将量子光学传感领域的最新进展融入频率梳计量技术，实现了在前所未有的 2.5 太赫兹光学带宽内，量子噪声降低量达 2.9 分贝（低于散粒噪声极限）的量子增强型模式分辨双梳光谱技术。我们的简易实验方案采用高亮度克尔压缩和共线光谱技术，实现了近期理论提案中未预测到的显著计量优势。因此，本研究将推动探索量子增强型光学频率梳计量与光谱技术极限的相关研究。例如，可在不同梳功率范围内对其他双梳光谱几何结构进行评估，并结合不同平台实现更高水平的压缩。尽管已知光纤中的拉曼效应会限制可实现的压缩水平（43），但这些效应在纳米光子压缩平台 [如氮化硅（44）] 中可能影响较小。

此外，本研究为探索量子增强型双梳光谱技术可实现的更高信噪比奠定了基础。为了最大化信噪比，两个光学频率梳应实现功率匹配。然而，这对数字处理提出了挑战，因为单个模数转换器（ADC）无法同时记录中心脉冲和量子受限电噪声本底。克服这一限制的一种方法是结合多个模数转换器，以实现更宽的动态范围（45）。目前已有相关技术正在探索中，以提高交叉梳光谱技术的动态范围（46）。正如我们在补充材料中所述，通过提高模数转换器的动态范围并实现光学频率梳的功率匹配，在共线双梳光谱实验中，对两个光学频率梳均进行压缩可实现最大信噪比。在共线实验中，两个功率匹配的压缩光学频率梳有望实现约 7 分贝的量子噪声降低，这是克尔光纤压缩的最高水平（43）。

为了进一步最大化信噪比，还应研究量子增强型双梳光谱技术是否与多副本（6）和 / 或频分复用双梳光谱技术（25）兼容。压缩双梳光谱技术将拥有众多即时应用场景，包括改进快速反应动力学表征（4）、降低生物样品光谱成像的功率水平（23），以及提高信噪比以克服探测器非线性带来的限制（3）。对于样品吸收较弱且信噪比要求较高的情况，量子增强型双梳光谱技术将成为大气压下痕量气体分析的关键技术（22）。此外，量子增强型双梳光谱技术还将减少时间分辨实验中获取高信噪比背景光谱所需的时间（4）。

本研究的测量范围覆盖 2.5 太赫兹，但许多应用将受益于更宽光学带宽的压缩态，正如近期纳米光子技术所展示的那样（17）。作为傅里叶变换光谱技术的一种改进形式，双梳光谱技术具有更高的速度、灵敏度和频率轴可溯源性，为痕量气体传感、光谱成像和工业分析提供了众多机遇。尽管傅里叶变换光谱技术已开始利用单光子态（47），但尚无任何傅里叶变换光谱技术利用过高亮度压缩态。我们对双梳光谱量子噪声的深入理解，推动了整个量子傅里叶变换光谱技术的发展。最后，本研究成果将为光学频率校外差和零差技术的量子增强版本提供参考，这些技术可应用于距离计量、光学时钟比较和光学时间传递等领域。

参考文献与注释

S. A. Diddams, K. Vahala, T. Udem, Science 369, eaay3676 (2020).
N. Picqué, T. W. Hänsch, Nat. Photonics 13, 146–157 (2019).
I. Coddington, N. Newbury, W. Swann, Optica 3, 414–426 (2016).
N. Hoghooghi et al., Optica 11, 876–882 (2024).
C. Zhang et al., Nature 633, 63–70 (2024).
M. Walsh, P. Guay, J. Genest, APL Photonics 8, 071302 (2023).
B. Xu, Z. Chen, T. W. Hänsch, N. Picqué, Nature 627, 289–294 (2024).
E. D. Caldwell et al., Nature 618, 721–726 (2023).
E. S. Polzik, J. Carri, H. J. Kimble, Phys. Rev. Lett. 68, 3020–3023 (1992).
H. Shi et al., NPJ Quantum Inf. 9, 1–12 (2023).
A. Belsley, Phys. Rev. Lett. 130, 133602 (2023).
O. Pinel et al., Phys. Rev. Lett. 108, 083601 (2012).
C. Riek et al., Nature 541, 376–379 (2017).
M. A. Guidry, D. M. Lukin, K. Y. Yang, R. Trivedi, J. Vučković, Nat. Photonics 16, 52–58 (2022).
N. C. Menicucci, S. T. Flammia, O. Pfister, Phys. Rev. Lett. 101, 130501 (2008).
S. Wang et al., Phys. Rev. A 98, 053821 (2018).
R. Nehra et al., Science 377, 1333–1337 (2022).
M. Rosenbluh, R. M. Shelby, Phys. Rev. Lett. 66, 153–156 (1991).
C. X. Yu, H. A. Haus, E. P. Ippen, Opt. Lett. 26, 669–671 (2001).
M. Fiorentino, J. E. Sharping, P. Kumar, D. Levandovsky, M. Vasilyev, Phys. Rev. A 64, 031801 (2001).
N. Kalinin et al., Nanophotonics 12, 2945–2952 (2023).
F. R. Giorgetta et al., Laser Photonics Rev. 15, 2000583 (2021).
T. Ideguchi et al., Nature 502, 355–358 (2013).
I. E. Gordon et al., J. Quant. Spectrosc. Radiat. Transf. 277, 107949 (2022).
N. R. Newbury, I. Coddington, W. Swann, Opt. Express 18, 7929–7945 (2010).
M. Walsh et al., in Optica Sensing Congress 2023 (AIS, FTS, HISE, Sensors, ES) (Optica Publishing Group, 2023), p. JTh1A.1.
P. J. Winzer, J. Opt. Soc. Am. B 14, 2424–2429 (1997).
F. Quinlan et al., Nat. Photonics 7, 290–293 (2013).
J.-D. Deschênes, J. Genest, Phys. Rev. A 87, 023802 (2013).
N. Lordi, E. J. Tsao, A. J. Lind, S. A. Diddams, J. Combes, Phys. Rev. A 109, 033722 (2024).
H. A. Haus, Electromagnetic Noise and Quantum Optical Measurements (Springer, 2000).
D. T. D. Childs et al., Appl. Spectrosc. Rev. 50, 822–839 (2015).
材料和方法详见补充材料。
W. Jia et al., Science 385, 1318–1321 (2024).
J. Junker, D. Wilken, E. Huntington, M. Heurs, Opt. Express 29, 6053–6068 (2021).
V. D. Vaidya et al., Sci. Adv. 6, eaba9186 (2020).
S. F. Pereira, M. Xiao, H. J. Kimble, J. L. Hall, Phys. Rev. A. 38, 4931–4934 (1988).
H.-A. Bachor, T. C. Ralph, A Guide to Experiments in Quantum Optics (Wiley, 2019).
T. Tomberg, A. Muraviev, Q. Ru, K. L. Vodopyanov, Optica 6, 147–151 (2019).
J. Roy, J.-D. Deschênes, S. Potvin, J. Genest, Opt. Express 20, 21932–21939 (2012).
N. B. Hébert et al., Opt. Express 25, 8168–8179 (2017).
R. K. Cole, A. S. Makowiecki, N. Hoghooghi, G. B. Rieker, Opt. Express 27, 37920–37939 (2019).
R. Dong et al., Opt. Lett. 33, 116–118 (2008).
F. Gyger et al., Phys. Rev. Lett. 124, 013902 (2020).
P. F. Bernath, J. Quant. Spectrosc. Radiat. Transf. 186, 3–16 (2017).
C. P. Bauer et al., Nat. Commun. 15, 7211 (2024).
Y. Mukai, R. Okamoto, S. Takeuchi, Opt. Express 30, 22624–22636 (2022).
D. I. Herman et al., Squeezed dual-comb spectroscopy, Dryad (2024); https://doi.org/10.5061/dryad.4qrfj6qkc.

致谢

感谢 J.-D. Deschênes、C. Rau、S. Geller 和 A. Kyle 提供的有益讨论。感谢 J. Ye 和 N. Newbury 对稿件提出的宝贵意见。同时感谢 K. Cossel、I. Coddington 和 T.-H. Wu 出借技术设备。

资金支持：作者感谢美国国家科学基金会（NSF）QLCI 项目（资助号 OMA-2016244）和美国海军研究办公室（ONR）（资助号 N000142212438）的资金支持。E.J.T. 感谢 NDSEG 奖学金的支持。M.K.K. 和 M.H. 感谢美国国家科学基金会研究生研究奖学金项目的支持。M.W. 和 J.G. 感谢加拿大自然科学与工程研究委员会（NSERC）和魁北克量子光子学联盟（PQ2）的支持。

作者贡献：概念构思：D.I.H.、M.W.、M.K.K.、N.L.、E.J.T.、J.C.、J.G. 和 S.A.D.；方法设计：D.I.H.、M.W.、M.K.K.、A.J.L.、M.H.、J.G. 和 S.A.D.；软件开发：D.I.H.、M.W.、M.K.K. 和 J.G.；数据分析：D.I.H.、M.W.、M.K.K.、N.L.、J.C.、J.G. 和 S.A.D.；实验实施：D.I.H.、M.K.K.、M.W.、J.G. 和 S.A.D.；资源提供：J.G. 和 S.A.D.；初稿撰写：D.I.H.、M.K.K.、J.G. 和 S.A.D.；稿件修订与编辑：所有作者；图表制作：D.I.H.、M.K.K.、M.W.、J.G. 和 S.A.D.；项目指导：J.C.、J.G. 和 S.A.D.；项目管理：S.A.D.；资金获取：J.C. 和 S.A.D.。

利益冲突：作者声明无利益冲突。

数据与材料可用性：评估论文结论所需的所有数据均包含在论文图表和 / 或补充材料中。数据也可通过 Dryad（48）获取。

补充材料

详见science.org/doi/10.1126/science.ads6292，包含材料与方法、补充文本、图 S1 至 S9 以及参考文献（49-50）。

提交日期：2024 年 8 月 28 日；接受日期：2024 年 12 月 30 日；在线发表日期：2025 年 1 月 16 日

DOI：10.1126/science.ads6292

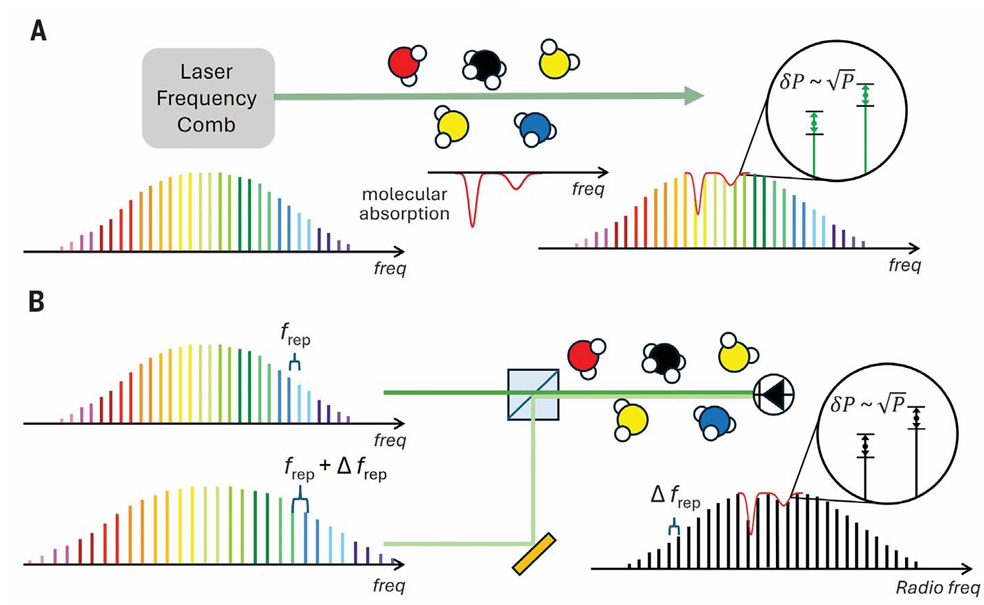
图 1：频率梳光谱与量子噪声

（A）直接光学频率梳（OFC）光谱示意图。分子吸收信息会印在光学频率梳上，其最终量子灵敏度极限由单个梳模上的幅度散粒噪声（δP ~ √P）决定。（B）两个重复频率存在差异（Δfᵣₑₚ）的光学频率梳发生干涉，可将光频与射频进行一一对应映射。光电探测器输出信号经傅里叶变换后，会生成射频梳信号。在此过程中，其最终灵敏度极限由射频梳模上的散粒噪声决定。

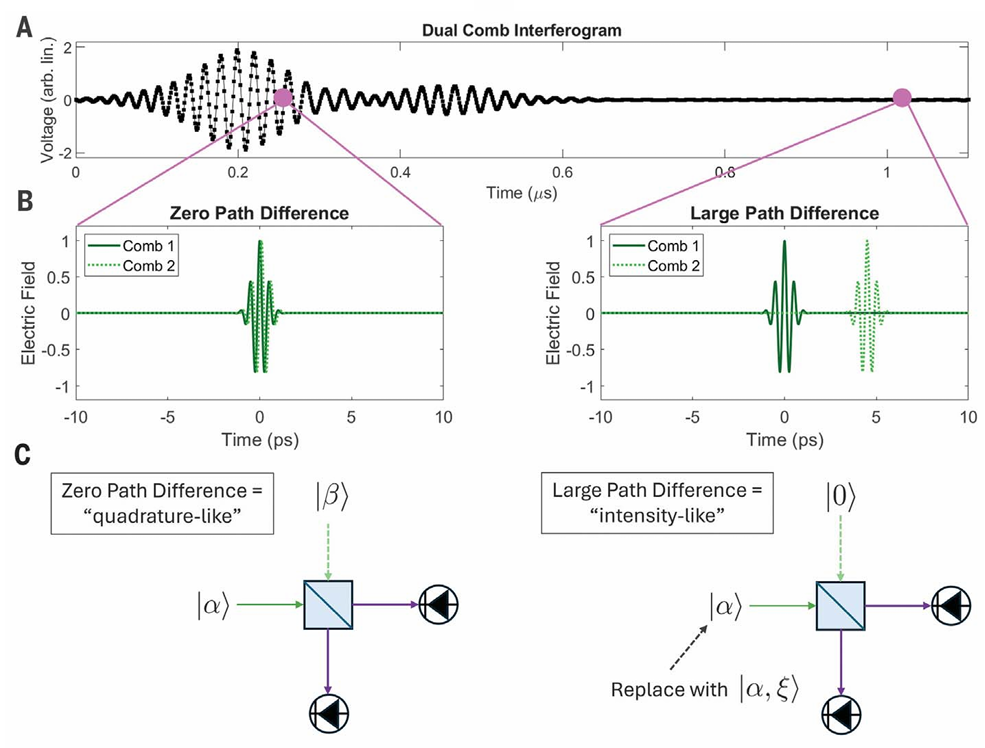
图 2：双梳干涉测量的时域量子测量示意图

（A）数字化干涉图，其中纵轴为实验室时间。每个干涉图数据点均源于两个双梳后续脉冲干涉重叠的积分结果。这一概念在（B）中得到进一步阐释，图中展示了零光程差（左侧）和大光程差（右侧）情况下产生干涉图的电场简化模型，横轴为有效光程分离时间。（C）两种极端情况下量子测量的简化单模示意图：在零光程差下，该测量具有 “类正交” 特性，类似于将强度分别为 |α|² 和 |β|² 的两个相干态在分束器上干涉所得到的测量结果；在大光程差下，该测量具有 “类强度” 特性，相当于将一个相干态与真空态（从任一光学频率梳的角度来看）进行干涉。若将相干态替换为强度为 |α|²、压缩因子为 x 的幅度压缩态，则可降低双梳测量的量子噪声（38）。

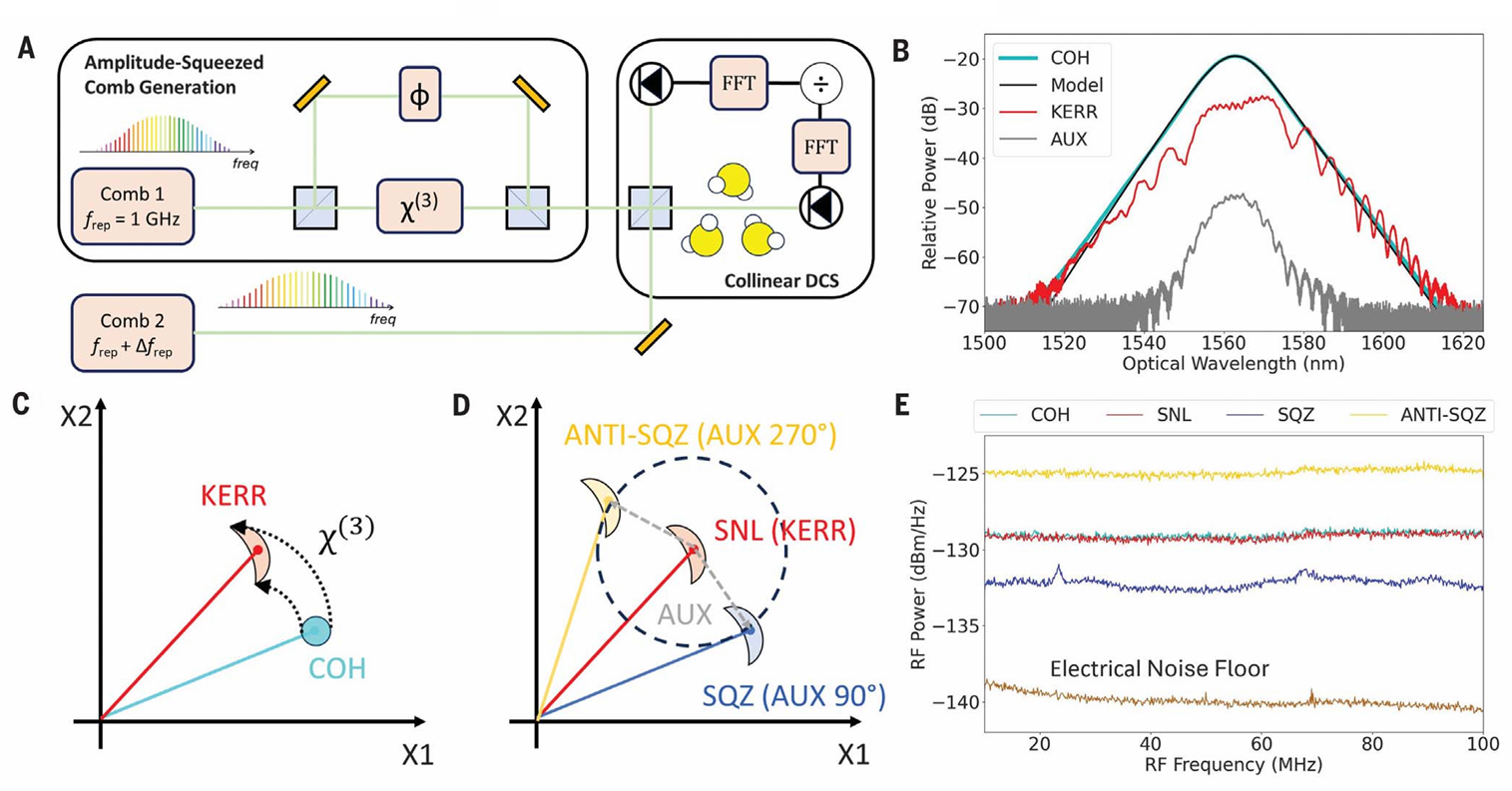图 3：双梳光谱（DCS）示意图与单梳压缩概念及结果

（A）量子增强型双梳光谱装置简化示意图。非线性马赫 - 曾德尔干涉仪生成幅度压缩频率梳，随后与相干态频率梳相结合。分子被置于双梳光束中的一束光路上，两束光均经过探测、数字化处理后进行快速傅里叶变换（FFT），最后将输出结果相除，得到量子增强型归一化透射光谱。（B）非压缩相干态光学频率梳（COH，浅蓝色，黑色曲线为孤子模型光谱）、强压缩脉冲（KERR，红色，经保偏高非线性光纤（PM-HNLF）传输后）以及弱辅助脉冲（AUX，灰色，经保偏高非线性光纤正交轴传输后）的光谱。（C）克尔（Kerr）压缩态生成的相空间图。与幅度相关的相移可将相干态（COH）转化为月牙形分布的克尔态（KERR）。X₁和 X₂代表玻色正交算符，分别类似于位置和动量。（D）辅助脉冲位移的相空间图。通过将克尔态（散粒噪声极限，SNL）按适当幅度和相位进行位移，可产生幅度反压缩态（ANTI-SQZ）或幅度压缩态（SQZ）。（E）相干态、克尔态、辅助脉冲位移压缩态和辅助脉冲位移反压缩态的光电流噪声电谱，棕色曲线为电噪声本底（33）。

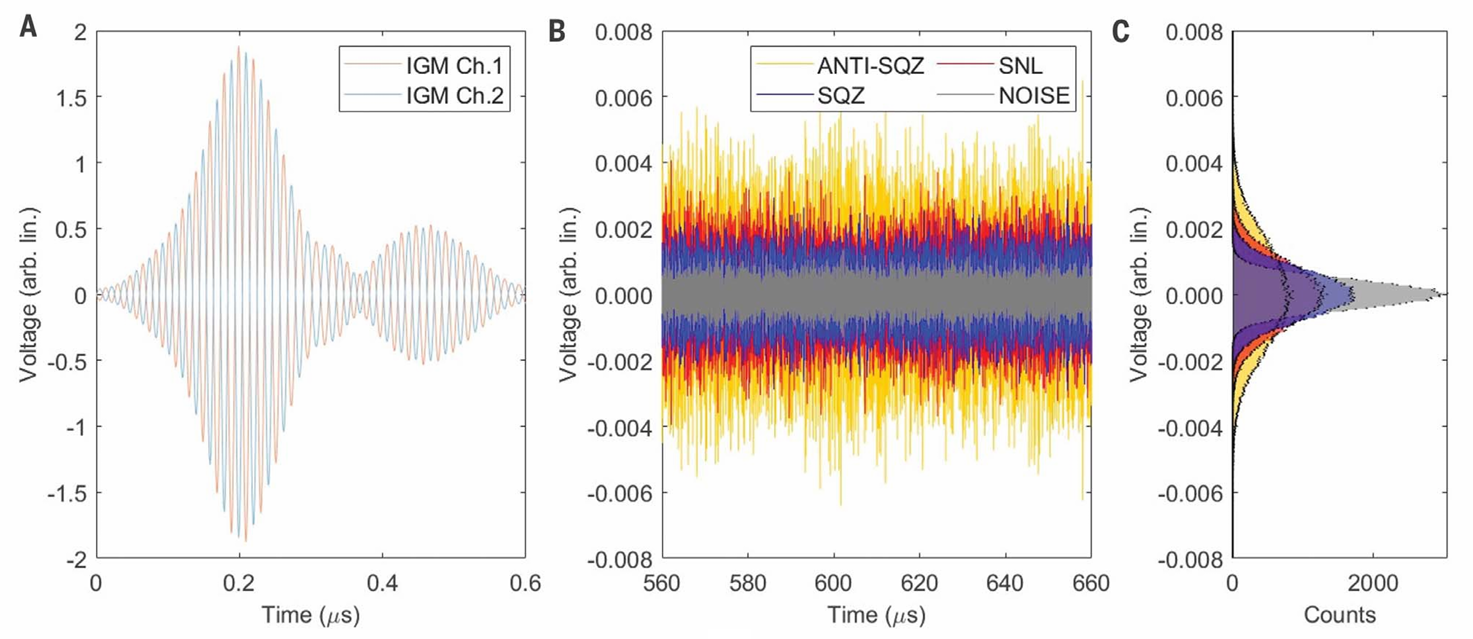图 4：双梳时域数据

（A）在合束器两侧生成的几乎完全相同的干涉图，注意两个干涉图之间存在 180° 的相移。这些干涉图已通过数字滤波处理（中心频率 50 MHz，带宽 20 MHz）。（B）在四种实验条件下，将两个探测器信号进行数字相加后，得到大光程差处的干涉图信号。其中，散粒噪声极限（SNL）为未位移的克尔态，同时还展示了位移后的压缩态（SQZ）和反压缩态（ANTI-SQZ），以及电探测链噪声本底（灰色曲线）。经估算，散粒噪声极限与压缩态之间的量子噪声降低量（QNR）为 2.6 dB。（C）（B）中电压噪声的直方图，清晰呈现了压缩态（SQZ）的量子噪声降低现象和反压缩态（ANTI-SQZ）的量子噪声放大现象。

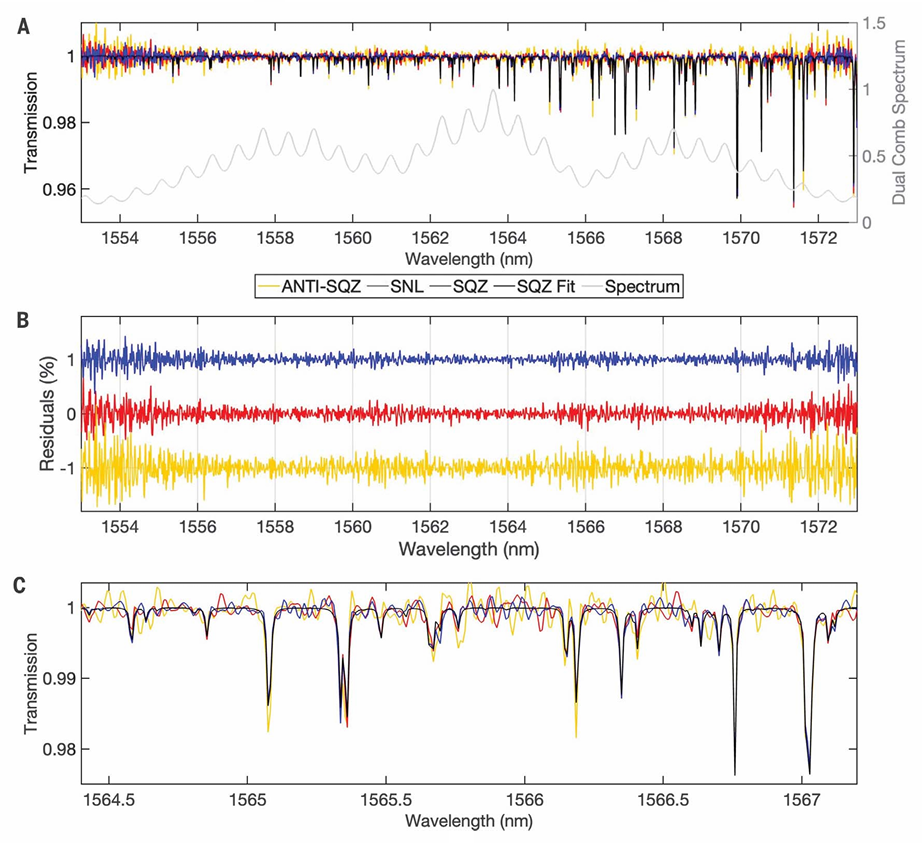图 5：双梳透射光谱与拟合结果

（A）通过对每个独立通道的傅里叶变换结果取比值，得到平均双梳透射光谱。该数据通过对 1112 个干涉图（约 198 ms 的数据采集时间）进行平均获得。黑色曲线为对压缩态（SQZ）数据集的拟合结果，从中可最清晰地观察到窄的硫化氢（H₂S）吸收特征；灰色曲线为其中一个通道的双梳光谱，用作参考。（B）展示了三种情况下的残差（透射率减去拟合值）：散粒噪声极限（SNL，红色曲线）、压缩态（SQZ，蓝色曲线）和反压缩态（ANTI-SQZ，黄色曲线）。在该平均条件下，量子噪声降低量约为 2.6 dB。残差噪声的变化源于上方所示双梳光谱中不均衡的功率分布。（C）对若干硫化氢吸收谱线的放大图，体现了数据与拟合程序的高质量匹配效果。

查看全文

http://www.dtcms.com/a/394998.html