LeetCode:47.从前序和中序遍历序列构造二叉树

目录

1.从前序和中序遍历序列构造二叉树

---

1.从前序和中序遍历序列构造二叉树

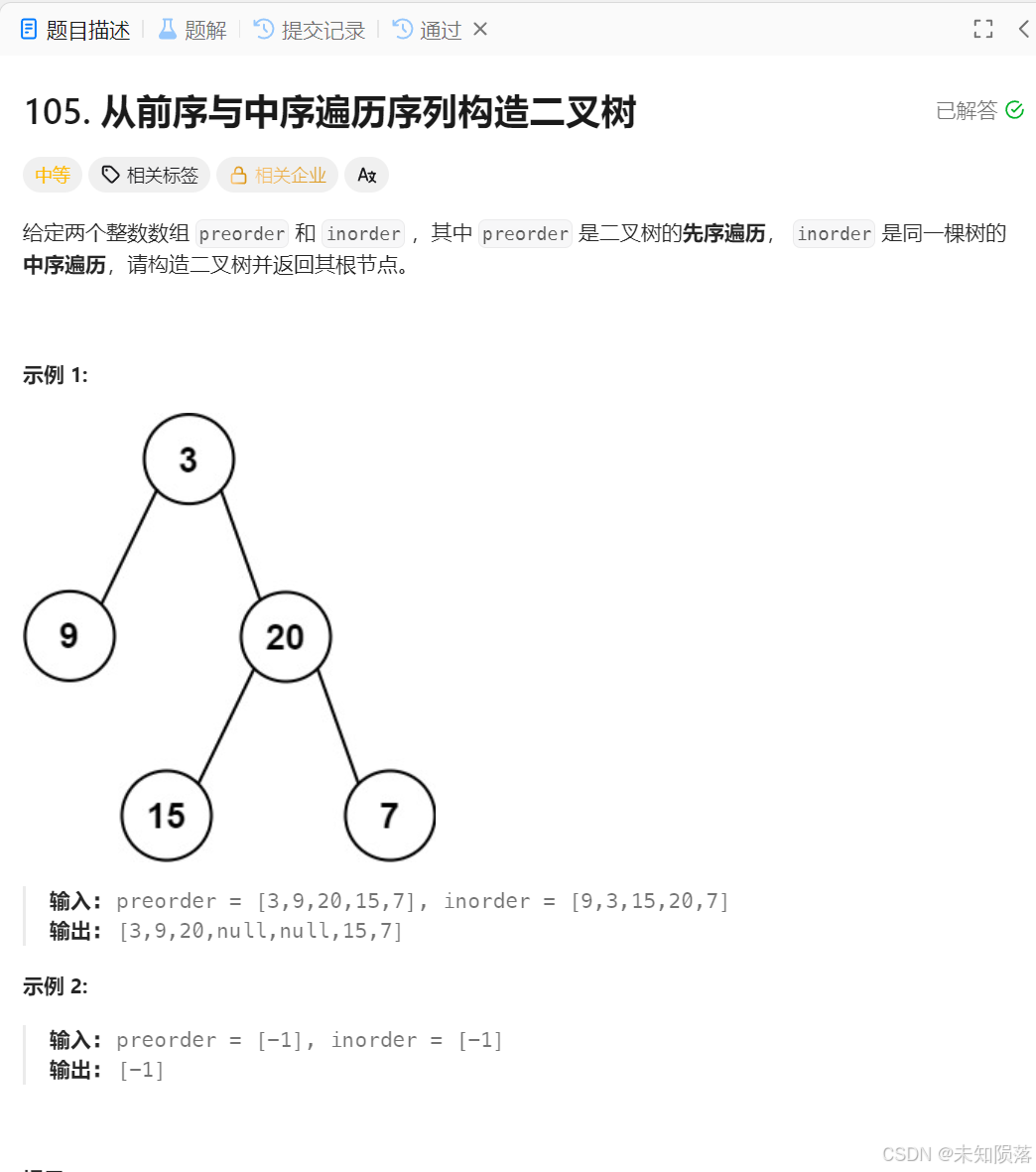
当给定了一个前序遍历和中序遍历后我们能够得到那些信息？

        首先前序遍历的第一个节点是根节点，当得知根节点后，可以将中序遍历分为两部分，左边的就是左子树的元素，右边的就是右子树的元素，而对于两颗子树来说也可以通过这种方式来不断进行分割子树

        所以这道题就可以通过递归的方式来解决，我们通过函数传入前序遍历以及左右边界，中序遍历以及左右边界，我们可以先通过哈希表来建设值和下标的映射关系，因为前序第一个元素就是根节点，很好确定，但是中序就只能通过值的映射来确定，当我们得知前序根的下标pre_root和中序的in_root，就可以用in_root - in_left来确定左子树的值了

        对于左子树来说，在前序遍历中的范围为【pre_left + 1, pre_left + left_size】，pre_left + 1表示跳过第一个根节点，pre_left + left_size表示左子树的节点数，而在中序遍历中范围为【in_left，in_root - 1】，起点很好理解，in_root就是根节点的下标 ，减一就表示左边的部分

        对于右子树来说，前序中【pre_left + left_size + 1, pre_right】，中序【in_root + 1, in_right】

class Solution {unordered_map<int, int> hash;
public:TreeNode* createTree(vector<int>& preorder, vector<int>& inorder, int pre_left, int pre_right, int in_left, int in_right){if(pre_left > pre_right || in_left > in_right) return nullptr;int pre_root = pre_left;int in_root = hash[preorder[pre_root]];int left_size = in_root - in_left;TreeNode* root = new TreeNode(preorder[pre_root]);root->left = createTree(preorder, inorder, pre_left + 1, pre_left + left_size, in_left, in_root - 1);root->right = createTree(preorder, inorder, pre_left + left_size + 1, pre_right, in_root + 1, in_right);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int n = inorder.size();for(int i = 0; i < n; i++)hash[inorder[i]] = i;return createTree(preorder, inorder, 0, n - 1, 0, n - 1);}
};