【Java.数据结构】初识集合框架

🎁个人主页：User_芊芊君子
🎉欢迎大家点赞👍评论📝收藏⭐文章
🔍系列专栏：Java.数据结构

【前言】

Java语法部分完结，现在开始进军数据结构部分，在Java编程中，数据结构与算法是高效程序的基石，集合框架是操作数据结构的便捷工具集。时间、空间复杂度是衡量算法效率的核心指标。本文旨在带大家初识Java集合框架，夯实复杂度认知，为后续学习筑牢基础。

一、初识数据结构

数据结构是组织和存储数据的方式，相互之间存在的一种或多种特定关系的数据元素的集合，不同结构对应着不同的查询，插入，删除效率。Java中的数据结构可分为线性数据结构和非线性结构两大类，其区别是数据元素之间的逻辑关系。

二、集合框架

1.什么是集合框架？

Java集合框架包括两种类型，一种是集合（Collection）,存储一个元素集合；另一种是图（Map），存储键值对数据

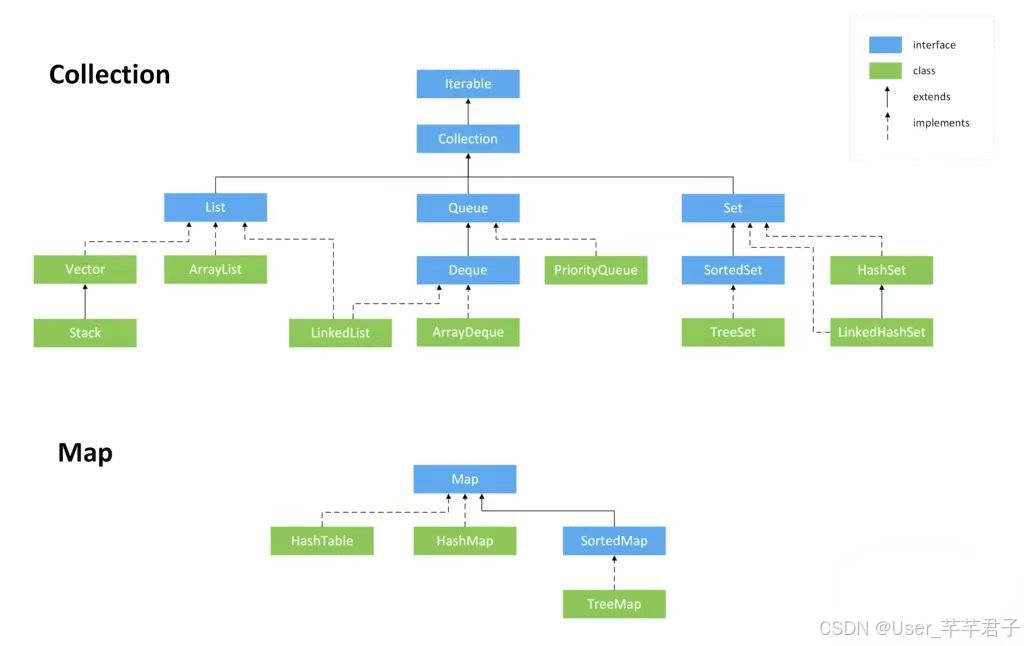
Java集合框架是对常用数据结构的封装，是位于java.util包下的一组接口和其实现类，相当于容器，主要表现为：将多个元素置于一个单元中，用于对这些元素进行快速，便捷的储存，检索，管理，即增删查改

• 常见的集合框架相关组件：

1. Collection：是⼀个接⼝，包含了⼤部分容器常⽤的⼀些⽅法
2. List：是⼀个接⼝，规范了ArrayList和LinkedList中要实现的⽅法

• ArrayList：实现了List接⼝，底层为动态类型顺序表
• LinkedList：实现了List接⼝，底层为双向链表

3. Stack：底层是栈，栈是⼀种特殊的顺序表
4. Queue：底层是队列，队列是⼀种特殊的顺序表
5. Deque：是⼀个接⼝
6. Set：集合，是⼀个接⼝，⾥⾯放置的是K模型

• HashSet：底层为哈希桶，查询的时间复杂度为O(1)
• TreeSet：底层为红⿊树，查询的时间复杂度为O(),关于key有序的
  7. Map：映射，⾥⾯存储的是K-V模型的键值对
• HashMap：底层为哈希桶，查询时间复杂度为O(1)
• TreeMap：底层为红⿊树，查询的时间复杂度为O()，关于key有序

2.集合框架的重要性

• 成熟的集合框架，有助于我们写出更加便捷，高效，稳定的代码
• 笔试和面试中基本都有所涉及

三、什么是算法？

算法（Algorithm）:是一组明确的，有限的，可执行的步骤，用于解决特定问题或完成特定任务，详细说明输入到输出的处理过程，他必须具备的特征：

• 有穷性：必须在有限步骤后终止
• 确定性：每个步骤都有明确定义
• 可行性：可以通过基本操作实现
• 输入：有零个或多个输入 输出：至少有一个输出

四、时间复杂度

算法的效率分为两种：时间效率和空间效率，也就是时间复杂度和空间复杂度。

1.时间复杂度

时间复杂度是用来衡量算法执行时间随输入规模增长而变化的度量标准。它描述了算法在最坏情况下所需的时间与输入数据量之间的关系，通常用大O符号表示。常见的时间复杂度包括==O(1)、O(log n)、O(n)、O(n log n)、O(n²)==等，这些分类反映了不同算法的效率特征。

2.⼤O的渐进表⽰法

算法中，语句运行的次数越多，代码的运行时间越长，但我们只需要计算大概的执行次数，因此引入了⼤O的渐进表⽰法，可以去掉那些影响不大的项

 public static void func(int N){int count = 0;//N^2for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {count++;}}// 5*Nfor (int i = 0; i < 5*N; i++) {count++;}//100int M = 100;while ((M--)>0){count++;}System.out.println(count);}public static void main(String[] args) {func(10);}

F(N) = N^2 + 5*N +100

⼤O的渐进表⽰法规则：

• ⽤常数1取代运⾏时间中的所有加法常数。
• 在修改后的运⾏次数函数中，只保留最⾼阶项。
• 如果最⾼阶项存在且不是1，则去除与这个项⽬相乘的常数。得到的结果就是⼤O阶。

算法的时间复杂度存在最坏，最好，和平均情况：

最坏情况：任意输⼊规模的最⼤运⾏次数(上界)
最好情况：任意输⼊规模的最⼩运⾏次数(下界)

3.示例

【示例1】

void func(int N){int count = 0;for (int i = 0; i < 6*N; i++) {count++;}int M = 100;while ((M--)>0){count++;}System.out.println(count);}

• F(N) = 6*N + 100;
• （只保留最高阶项，并且去除常数6）
• 时间复杂度为O(N)

【示例2】

void func(int N, int M) {int count = 0;for (int k = 0; k < M; k++) {count++;}for (int k = 0; k < N ; k++) {count++;}System.out.println(count);
}

• F(N) = M+N;
• 第一个for循环中count执行了M次，第二个for循环中count执行了N次
• 所以时间复杂度为：O(M+N)

【示例3】

void func4(int N) {int count = 0;for (int k = 0; k < 100; k++) {count++;}
}System.out.println(count);
}

• F(N) = 100;
• k执行100次,但与N无关
• 时间复杂度为O(1)

【示例4】冒泡排序

oid bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}

• 让 array.lenth 为N,
• 外层循环：end执行N-1次（因为end从N减到1）
• 内层循环：（N-1)+(N-2)+…+1,等差数列得出
  时间复杂度：O(N^2)

【示例5】二分查找

int binarySearch(int[] array, int value) {int begin = 0;int end = array.length - 1;while (begin <= end) {int mid = begin + ((end-begin) / 2);if (array[mid] < value)begin = mid + 1;else if (array[mid] > value)end = mid - 1;elsereturn mid;}return -1;
}

最坏的情况：
二分查找每次都是对半查询
n，n/2^1 , n/2^2 … n/2^x=1
n=2^x
2^x=n
x=log_2(n)
时间复杂度为O(log_2(n))

【示例6】递归
递归的时间复杂度 = 递归执行的次数 * 每次递归执行的次数

long factorial(int N) {return N < 2 ? N : factorial(N-1) * N;}

每次 return 执行的次数为N，return 执行之后，不满足 N<2的，进行递归，直到N<2,也就是N=1
时间复杂度：N*O(1)=O(N)

【示例7】斐波那契

int fibonacci(int N) {return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);}

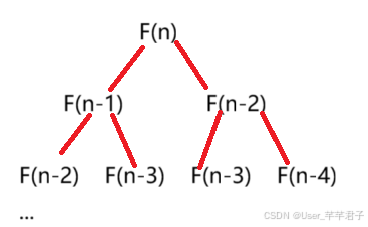
1，2，4…
2^0 , 2^1, 2^2…2(n-1)
等比数列
时间复杂度：O(2^n)

五、空间复杂度

空间复杂度（Space Complexity）是衡量算法在运行过程中临时占用存储空间大小的指标，通常用大O符号表示。它用于评估算法执行时所需的额外内存资源，与时间复杂度共同构成算法效率分析的核心维度。
【示例1】冒泡排序

void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if(sorted ==true)break;}}

• 随着问题的规模变大，变量并没有增多，没有申请新的内存，空间没有变大
• 空间复杂度：O(1)

【示例2】斐波那契

int[] fibonacci(int n) {long[] fibArray = new long[n + 1];fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; i++) {fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;}

• 随着问题的规模n变大，数组变大
• 空间复杂度：O(N)

【示例3】递归

long factorial(int N) {return N < 2 ? N : factorial(N-1)*N;}

• 每递归一次函数，开辟一次栈帧
• 空间复杂度：O(N)

六、总结

本文初探了Java集合框架与时间、空间复杂度。集合框架提供了List、Set、Map等多样数据结构，满足不同数据操作需求。时间、空间复杂度为算法效率评估提供科学依据。掌握这些知识，能助力我们合理选用集合、优化算法，编写高效Java程序。后续可深入源码与复杂算法分析，进一步提升能力。