因果推断:关于工具变量的案例分析
本篇文章Understanding Instrumental Variables适合希望了解因果推断的读者。文章的技术亮点在于使用工具变量(IV)方法来估计因果效应,尤其是在无法随机分配处理的情况下,展示了如何通过“鼓励设计”来进行有效分析。方法适用场景包括在线订阅、保险合同等无法随机化的设置。实际案例中,作者通过一个关于产品公司订阅通知的例子,成功演示了如何使用IV方法评估订阅对消费的影响,提供了清晰的步骤和数据分析。
文章目录
- 1 引言
- 2 案例分析
- 2.1 评估订阅计划案例
- 2.2 鼓励设计
- 2.3 工具变量 (IV)
- 2.4 IV 扩展
- 2.5 IV 的局限性
- 3 结论
1 引言
A/B 测试是因果推断的黄金标准,因为它们在最小假设下通过随机化允许我们做出有效的因果陈述。实际上,通过随机分配处理(药物、广告、产品等),我们能够比较主体(患者、用户、客户等)的感兴趣结果(疾病、公司收入、客户满意度等),并将结果的平均差异归因于处理的因果效应。
然而,在许多情况下,由于伦理、法律或实际原因,无法随机化处理。一个常见的在线场景是按需功能,例如订阅或高级会员资格。其他情况包括我们无法区分客户的功能,如保险合同,或那些根深蒂固以至于实验可能不值得投入的功能。在这些情况下,我们还能进行有效的因果推断吗?
答案是肯定的,这要归功于工具变量和相应的实验设计,称为鼓励设计。在上述许多情况下,我们无法随机_分配_处理,但我们可以_鼓励_客户接受它。例如,我们可以提供订阅折扣,或者我们可以改变选项的呈现顺序。虽然客户保留了是否接受处理的最终决定权,但我们仍然能够估计因果处理效应。让我们看看如何实现。
2 案例分析
2.1 评估订阅计划案例
在文章的其余部分,我们将使用一个玩具示例。假设我们是一家产品公司,开始发布每周时事通讯以推广产品和功能更新。我们想了解时事通讯是否值得投入,以及它最终是否成功地增加了销售额。不幸的是,我们无法进行标准的 A/B 测试,因为我们无法强迫客户订阅时事通讯。这是否意味着我们无法评估时事通讯?不完全是。
让我们假设我们还在我们的移动应用程序上对一个新的通知进行了 A/B 测试,该通知推广时事通讯。我们客户的随机样本收到了通知,而随机样本没有收到。也许这个 A/B 测试根本与评估时事通讯的因果效应无关,正如在大型公司中经常发生的那样。然而,对于对理解时事通讯对销售额影响感兴趣的数据科学家来说,这是一个绝佳的机会。
让我们首先看看数据。我从 src.dgp 导入数据生成过程,并从 src.utils 导入一些绘图工具。
dgp = dgp_notification_newsletter(n=10_000)
df = dgp.generate_data()
df.head()
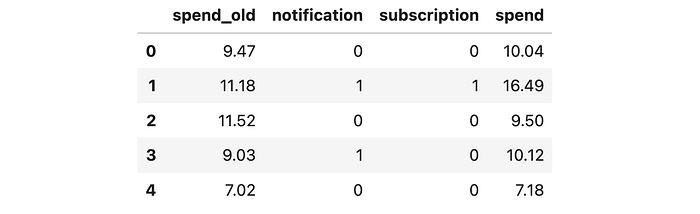
我们有关于 10,00010,00010,000 名客户的信息,我们观察他们是否收到了 notification,是否 subscribed 到时事通讯,以及他们 spent 了多少钱。此外,我们还观察了他们在订阅计划引入之前 spent_old 了多少钱。在文章的其余部分,我们将这些变量标记如下:
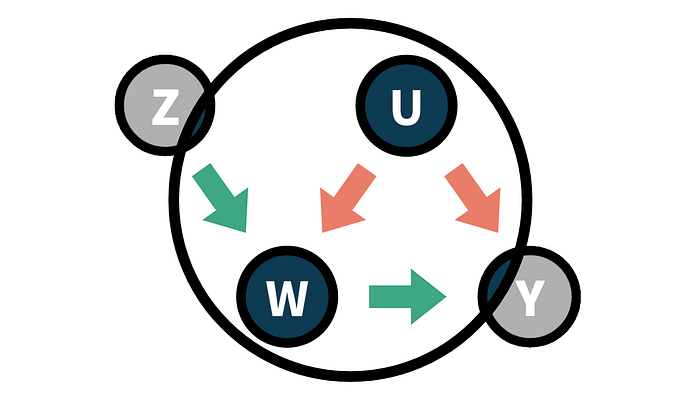
notification,处理分配,ZZZsubscription,处理状态,WWWspend_old,特征或控制变量,XXXspend,结果,YYY
一个天真的方法是比较 subscribed 的客户和未订阅的客户在 spend 上的差异。相应的因果对象或_估计量_是
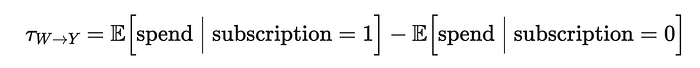
让我们可视化这两个组的平均 spend。
plot_group_comparison(df, x="subscription", y="spend", title="Spend", xticks=["Non-subscriber", "Subscriber"])
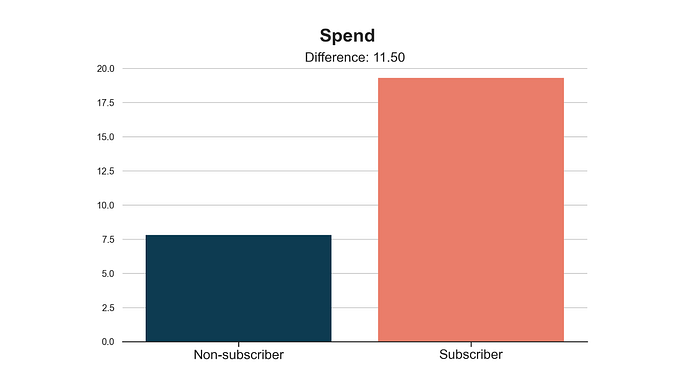
订阅者平均比非订阅者多花费 11.511.511.5。但这是否是因果效应?
我们可以想象,那些更活跃、对我们产品更感兴趣的客户也会更愿意了解产品新闻。例如,我们可以想象,那些有更多预算可供消费的客户也会希望更好地消费并订阅时事通讯。
我们可以用以下有向无环图 (DAG) 表示变量之间的关系。
在图中,我们用圆圈表示变量,用箭头表示因果关系。
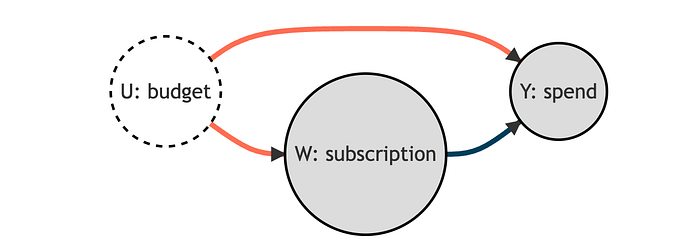
从技术上讲,客户的预算是一个不可观测的混杂因素,它在我们的处理 subscription 和结果客户的 spend 之间开辟了一条虚假路径。因此,我们无法将 11.511.511.5 的均值差异估计解释为因果关系。
我们能做什么?
2.2 鼓励设计
不幸的是,我们无法进行 A/B 测试,因为我们无法强迫人们订阅时事通讯。然而,我们可以_鼓励_人们订阅。例如,我们可以向他们发送一个移动通知来宣传时事通讯。这种设置被称为鼓励设计,因为我们不随机化处理,而是随机化鼓励。在这种情况下,鼓励,即 notification,也称为工具变量。
重要的是要强调,虽然是随机分配的,但鼓励与感兴趣的处理_不_对应。事实上,有些人即使收到通知也_不会_订阅,而有些人即使_没有_收到通知也会订阅。
添加鼓励,即 notification 后,数据生成过程可以用以下 DAG 表示。
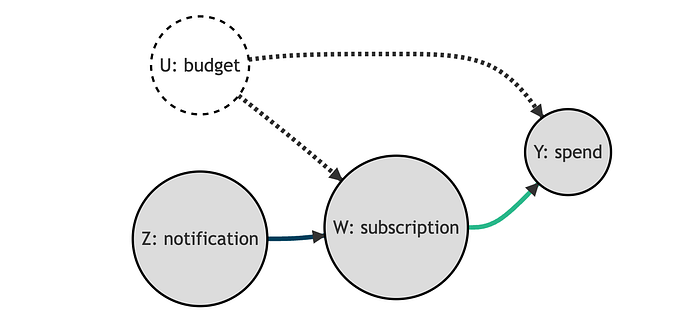
请注意,现在我们已经关闭了 subscription 和 spend 之间的开放路径。因此,我们可以估计订阅对销售概率的因果效应。让我们看看如何实现。
首先,我们想了解 notification 是否有效。这通常被称为工具的强度。由于随机化,我们可以将收到 notification 的人与未收到的人之间 spend 的平均差异归因于处理本身。
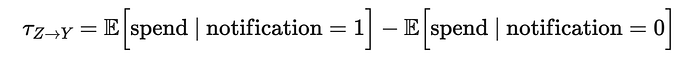
让我们可视化相应的均值差异估计。
plot_group_comparison(df, x="notification", y="spend", title="Spend", xticks=["No Notification", "Notification"])
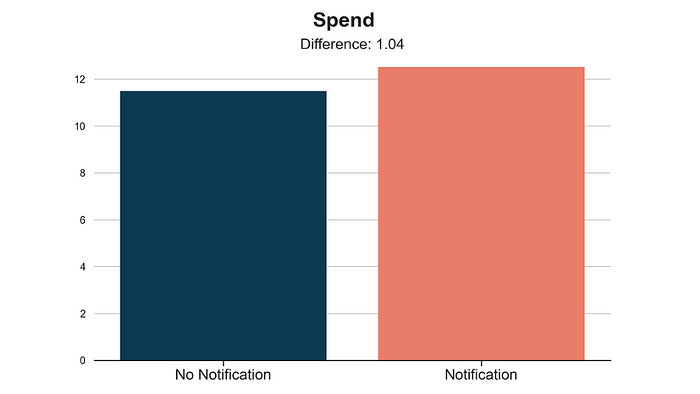
似乎收到 notification 的客户平均比未收到通知的客户多花费 111。这比我们之前估计的 11.511.511.5 要低得多。
然而,notification 对 spend 的影响并不是我们感兴趣的。我们更想知道 subscription 对 spend 的影响。事实上,并非所有收到电子邮件的客户都订阅了时事通讯。反之,有些人即使没有通知也订阅了时事通讯。
这意味着我们刚刚计算的效果被稀释了,因为有些人不遵守我们的激励,即 notification。我们必须将其_仅_归因于那些因为时事通讯而改变主意的客户。这些客户有多少?
让我们计算按处理组划分的 subscription 概率。
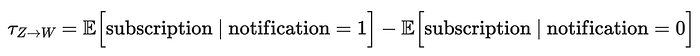
plot_group_comparison(df, x="notification", y="subscription", title="Subscription Probability", xticks=["No Notification", "Notification"])
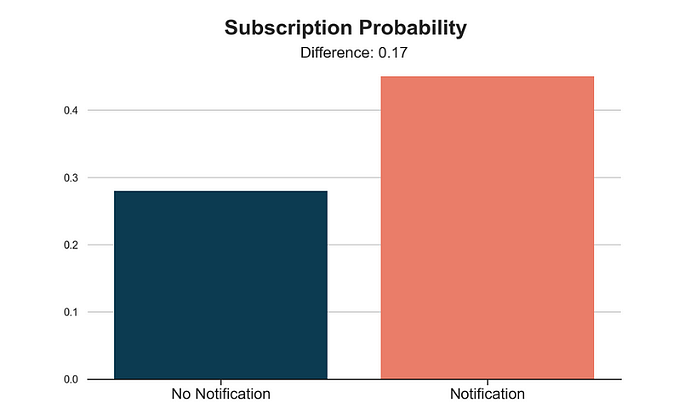
收到 notification 的客户有 17%17\%17% 更高的 subscription 概率。换句话说,似乎 notification 能够让 17%17\%17% 的客户改变主意。从对照组我们了解到,其中 28%28\%28% 的人无论如何都会订阅,而我们未能说服其余的 55%55\%55%。
我们现在拥有进行主要分析所需的所有要素
2.3 工具变量 (IV)
在这种情况下,对于一个二元工具 notification,一个二元处理 subscription 决策,以及 50−5050-5050−50 的处理分配概率,我们可以非常简单地直观理解工具变量是如何工作的。
我们有四组客户,取决于他们是否收到通知,以及他们是否订阅。
df.groupby(["notification", "subscription"]).agg(spend=("spend", "sum"), customers=("spend", "count")).iloc[::-1].T.round(0)
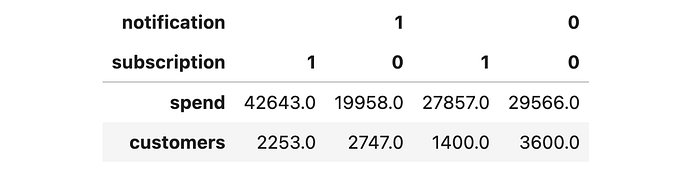
让我们可视化每个桶中的总花费和客户总数。
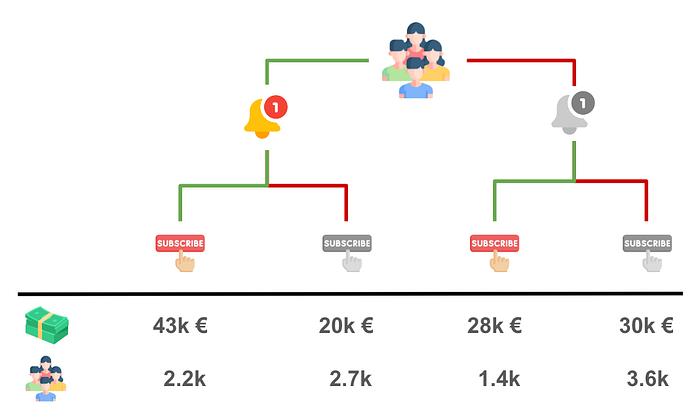
比较处理 (notification) 和对照组,我们看到通知使 spend 增加了 5k€5k€5k€ (43+20−28−3043 + 20 - 28 - 3043+20−28−30)。为了恢复感兴趣的因果效应,我们只需要将 5k€5k€5k€ 的增量 spend 归因于因为 notification 而决定 subscribe 的 800800800 (2200−14002200 - 14002200−1400) 名客户。结果恰好是 5k€/800=6€5k€ / 800 = 6€5k€/800=6€ 每位客户!
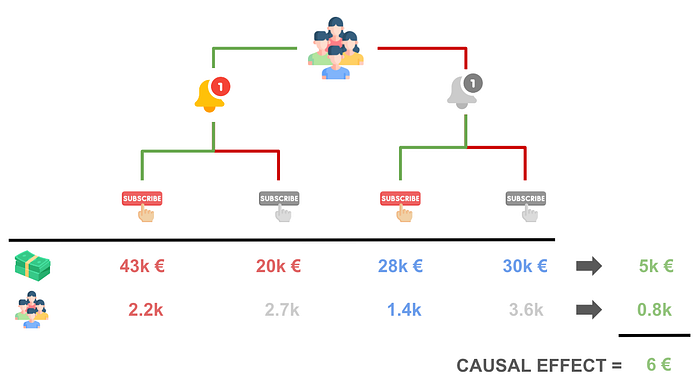
更一般地,IV 估计量由两个因果效应的比率给出:工具(或鼓励,或分配)ZZZ 对结果 YYY 的效应,除以工具 ZZZ 对处理(或内生变量)WWW 的效应。

为了计算 IV 估计,我们用经验平均值替换期望值。实际上,在我们的例子中,我们只需将上一节图中计算的两个均值差异估计值相除。
tau_ZY = df.loc[df.notification == 1, "spend"].mean() - df.loc[df.notification == 0, "spend"].mean()
tau_ZW = df.loc[df.notification == 1, "subscription"].mean() - df.loc[df.notification == 0, "subscription"].mean()
tau_ZY / tau_ZW
6.070222743259094
我们对 subscription 计划对 spend 影响的工具变量估计是 666,正如上面插图中所预期的那样!请注意,插图中的数学_仅_在精确 50−5050-5050−50 分配的特殊情况下有效。
更一般地,可以证明 IV 估计量的公式由协方差比率给出,
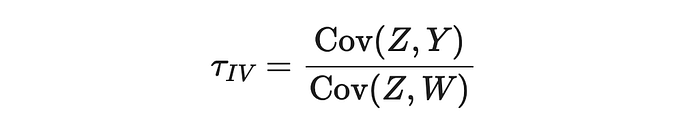
或者,用矩阵符号表示,
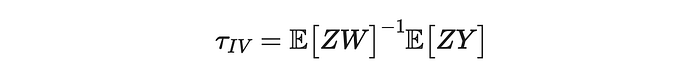
2.4 IV 扩展
如果我们有更多的工具或其他的控制变量会发生什么?例如,我们可以运行其他实验来鼓励客户 subscribe。或者,像我们这种情况,我们可以添加其他变量到模型中以提高预测准确性,例如之前的消费水平 spend_old。我们如何将它们包含在模型中?
简而言之,当我们有多个工具时,工具变量公式可以改写为
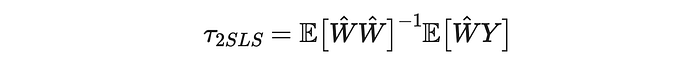
其中 W^\hat{W}W^ 是 WWW 在 ZZZ 上的投影,即实际上是给定处理分配的预测处理状态。这个预测步骤称为第一阶段。这个公式应该让您想起 OLS 估计量公式。确实,这等同于我们的结果 YYY 对预测处理 W^\hat{W}W^ 的线性回归,给定分配 ZZZ。这个步骤称为第二阶段。总的来说,由于估计过程可以分为两个独立的阶段,这被称为两阶段最小二乘 (2SLS) 估计量。
两阶段公式在大多数 IV 包的实现中尤为明显,我们将处理表示为对工具回归的结果。在 [IV2SLS](https://bashtage.github.io/linearmodels/iv/iv/linearmodels.iv.model.IV2SLS.html) 包中,这是通过使用方括号完成的。
from linearmodels.iv.model import IV2SLS as ivmodel_iv = iv.from_formula("spend ~ 1 + [subscription ~ notification]", data=df).fit()
model_iv.summary.tables[1]

我们可以验证这在代数上等同于首先将 subscription 对 notification 进行回归,然后将 spend 对预测的 subscription 概率进行回归。下面我们运行这两个回归并报告第二阶段的估计值。
model_1st_stage = smf.ols("subscription ~ 1 + notification", data=df).fit()
df["subscription_hat"] = model_1st_stage.predict(df)
model_2nd_stage = smf.ols("spend ~ 1 + subscription_hat", data=df).fit()
model_2nd_stage.summary().tables[1]

系数确实是相同的!
最后,上述两阶段公式也应该使额外协变量的包含变得相当直观。我们只需将协变量添加到两个阶段。
model_1st_stage = smf.ols("subscription ~ 1 + spend_old + notification", data=df).fit()
df["subscription_hat"] = model_1st_stage.predict(df)
model_2nd_stage_x = smf.ols("spend ~ 1 + spend_old + subscription_hat", data=df).fit()
model_2nd_stage_x.summary().tables[1]
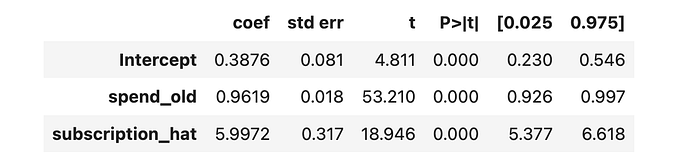
我们可以再次验证估计系数是相同的。
model_2sls = iv.from_formula("spend ~ 1 + spend_old + [subscription ~ notification]", data=df).fit()
model_2sls.summary.tables[1]
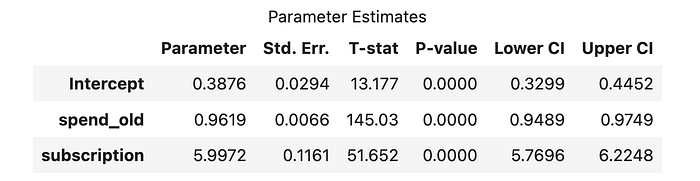
在回归中包含之前的消费水平确实将标准误差从 0.50.50.5 降低到 0.10.10.1。
2.5 IV 的局限性
本文分析的实验设置中,工具变量的主要局限性在于它们估计的是一个非常“特殊”的因果效应。正如我们在上一节中看到的,我们必须根据因为 newsletter 而决定 subscribe 的客户数量来重新调整总效应。这意味着我们只能估计总体中一个子集(依从者,即那些遵守我们的激励并因为激励而接受处理的客户)的效应。这组客户通常被称为依从者,相应的因果效应被称为局部平均处理效应 (LATE) 或依从者平均因果效应 (CACE)。
不幸的是,我们无法对那些即使没有 notification 也订阅了 newsletter 的客户(称为总是接受者)以及那些我们无法用 notification 说服的客户(称为从不接受者)发表任何看法。
IV 的另一个局限性在于其假设。在上一段中,我们讨论了三组客户:依从者(我们最喜欢的一组)、总是接受者和从不接受者。您可能已经注意到,这种特征化意味着存在第四组:反抗者。这些客户是如果他们没有收到 notification 就会订阅 newsletter 的客户。然而,由于通知,他们改变了主意,_反抗_了工具的意图。
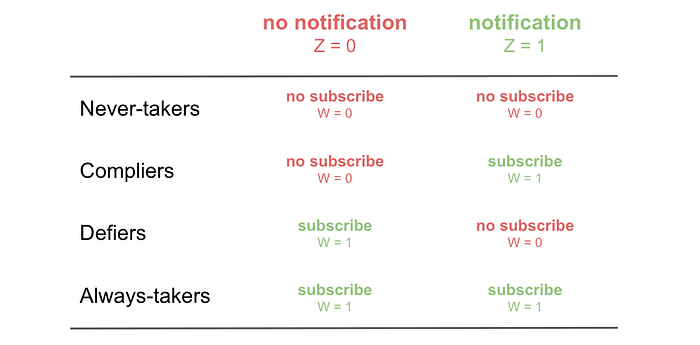
为了能够得出因果结论,我们必须假设实验中没有反抗者,否则我们的重新调整将是错误的,我们的估计将有偏差。
另一个隐藏的关键假设是通常所说的排他性限制。这个假设指出,工具 notification 仅通过处理 subscription 影响结果 spend。在我们设置中可能存在的违反情况是,如果通知_唤醒_了休眠用户。想象一个客户想要进行销售并已将商品添加到购物车,但忘记结账。订阅通知可能会提醒用户结账,从而直接影响 spend。正如您所想象的,IV 估计将有偏差,因为我们错误地将一些销售归因于 subscription,而它们是 notification 本身的_直接_效应。
3 结论
在本文中,我们介绍了实验设置中的工具变量。当我们由于伦理、法律或技术限制而无法随机化处理时,我们仍然可以考虑随机化激励以接受处理。这使我们能够做出因果陈述,但仅限于总体的一个子集,即依从者,也就是那些遵守我们的激励并因为激励而接受处理的客户。
值得注意的是,工具变量也可以用于观察性设置。然而,在这种情况下,我们在上一节中提到的排他性限制假设变得更难证明。事实上,我们需要一个这样的设置:我们的工具除了通过处理之外,不通过_任何其他_渠道影响结果。从技术上讲,排他性限制假设是
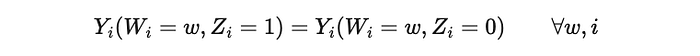
当我们不控制鼓励分配的设计时,这个假设更难证明。然而,如果满足,它为在全新设置中进行因果推断打开了大门。
