算法题（212）：01背包（空间优化）

审题：

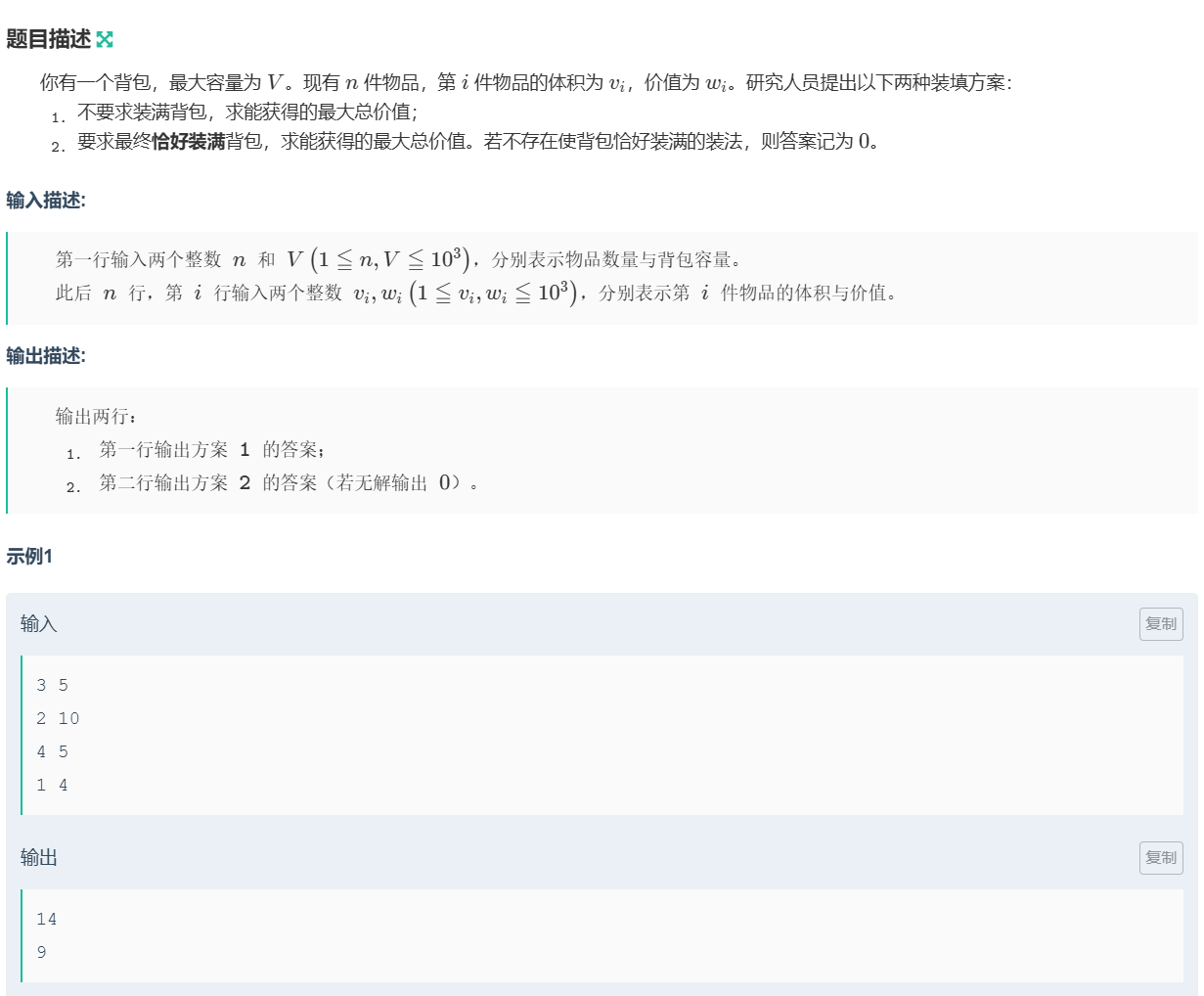
本题是01背包模板题

思路：
方法一：动态规划（空间优化）

本题解基于（算法题（212）：01背包-CSDN博客）继续进行优化分析

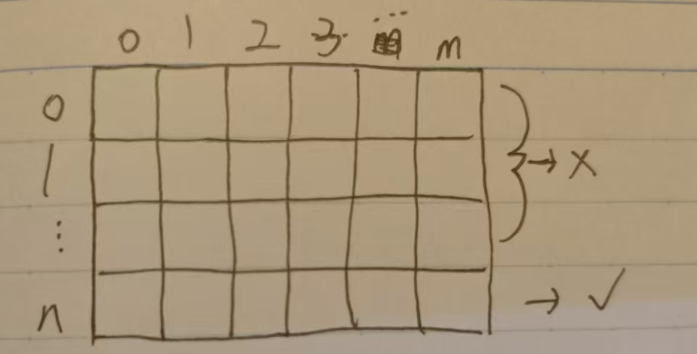
其实最后需要存储的数据只要有最后一行就行了，因为只要输出f[n][m]就行，那么我们就可以通过二维降一维的方法去存储数据，然后不断通过迭代计算去更新一维数组

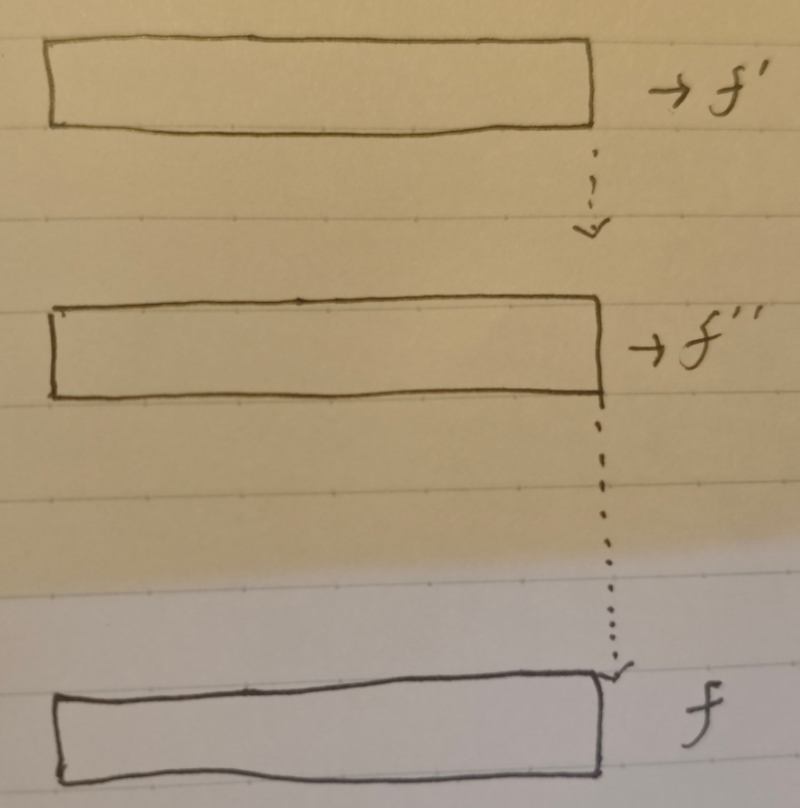
这里演示了从f'不断迭代为f的过程，从开始到结束一直都只有一个一维数组

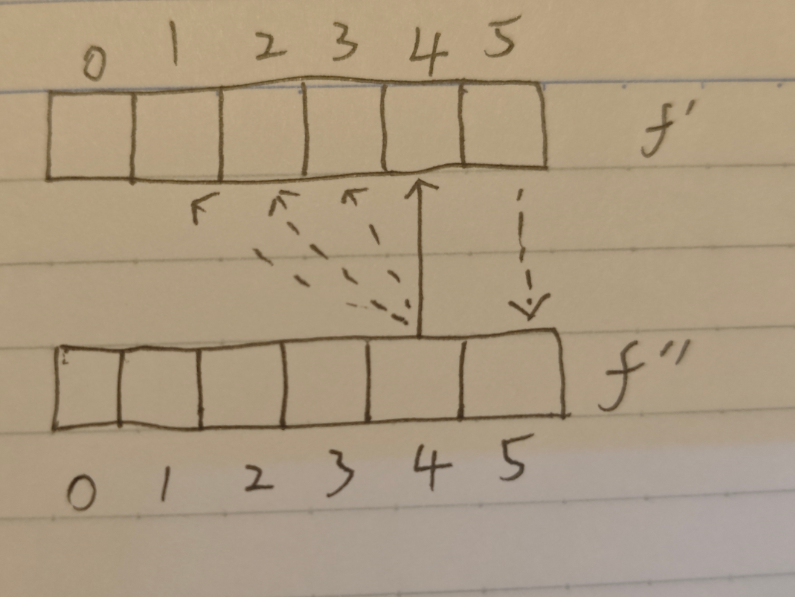
不过我们填表顺序就需要更改了，因为当前位置是依赖于上方和左上方的，所以我们需要从右往左进行更新，否则会导致数据更新错误

假设我们从左往右更新数据：

0号位置数据被改变后，可能依赖了0号位置更新的1号位置使用的就不是原来的0号位置数据，而是改变后的0号位置数据，也就相当于本来要用i-1行的数据，现在用成了第i行的数据更新，故该顺序错误

解题：

#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e3+10;
int n,m;
int w[N],v[N];
int f[N];//f[i][j]表示在包含1~n范围的物品中进行选择且保证体积和为j，所得到的最大价值
int main()
{//数据录入cin >> n >> m;for(int i = 1; i <= n; i++){cin >> v[i] >> w[i];}//question onefor(int i = 1; i <= n; i++){for(int j = m; j >= v[i]; j--){f[j] = max(f[j],w[i]+f[j-v[i]]);}}cout << f[m] << endl;//question twomemset(f,-0x3f3f3f3f,sizeof f);f[0] = 0;for(int i = 1; i <= n; i++){for(int j = m; j >= v[i]; j--){f[j] = max(f[j],w[i]+f[j-v[i]]);}}if(f[m] < 0) cout << 0 << endl;else cout << f[m] << endl;return 0;
}

注意：

降维改代码方法：首先将所有二维的信息改为一维，比如将二维数组改为一维数组，相关初始化也是同理更改，不过双层for循环要保留，毕竟要迭代n次。

然后本题需要更改填表顺序，我们也改一下，相关的if语句也融合进for循环中。而去掉一维后如果出现f[i]=f[i]之类的无效命令我们也可以直接删掉

【模板】01背包