【微实验】激光测径系列(三)
这篇主要探讨误差相关的内容——
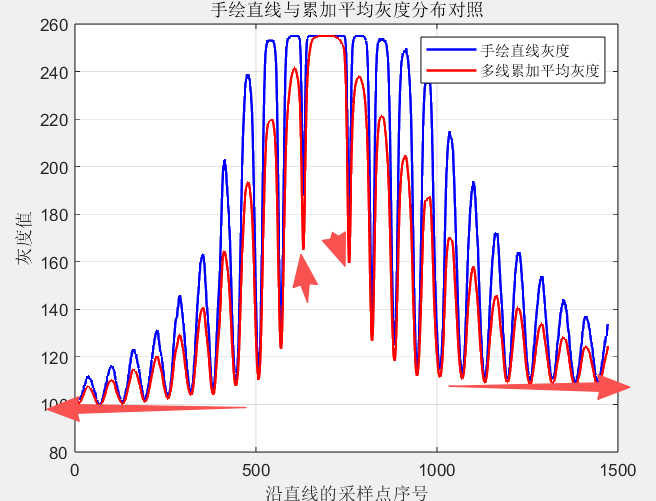
通过前面的实验,我们发现了所拍摄的图片,经过了高斯滤波处理后,也会存在夫琅禾费堰塞湖条纹并不对称,整体上一边高一边低,对于单个的波峰和波谷也是一边高一边矮。那么这种情况对于我们所测量的△x和最终计算的直径究竟有什么影响呢?
夫琅禾费衍射条纹不对称现象分析及对条纹间距和细丝直径测算影响
一、夫琅禾费衍射条纹不对称原因推测
(一)绘制的扫描直线方向与条纹实际分布并不重合
在实验中,若手动绘制的扫描直线方向与衍射条纹的实际分布方向存在偏差,那么在提取条纹灰度信息时,就会导致两侧条纹最小值不对称。例如,当条纹实际是严格水平分布,而绘制的扫描直线存在一定倾斜角度时,扫描线在不同位置穿越条纹的情况不同,一侧可能更多地穿过条纹的边缘区域,而另一侧可能更多地穿过条纹的中心区域,从而使得两侧条纹的最小值在灰度值上表现出差异。
这点在第一篇【微实验】激光测径(一)中也有写到——
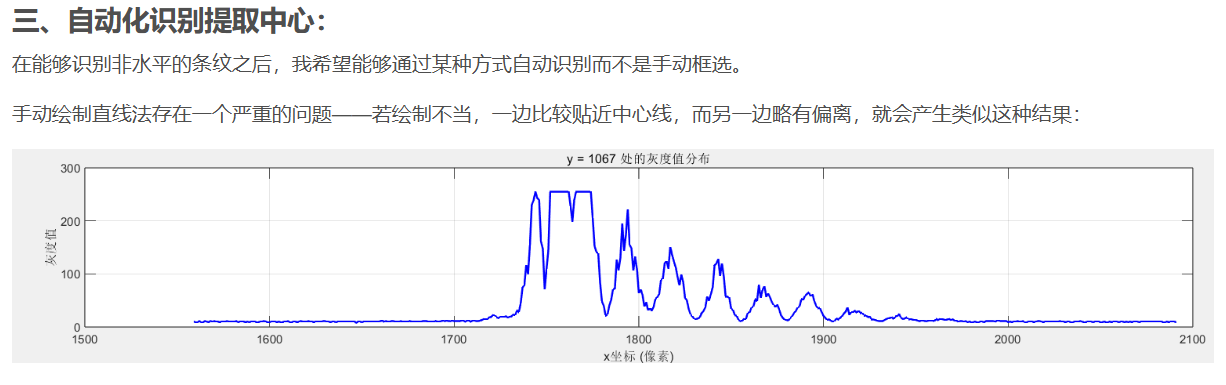
应用了自动提取条纹中心的程序后(虽然有的时候并不好用),但是在能够正确识别到衍射的情况下,它识别的会比手动画取更为准确。
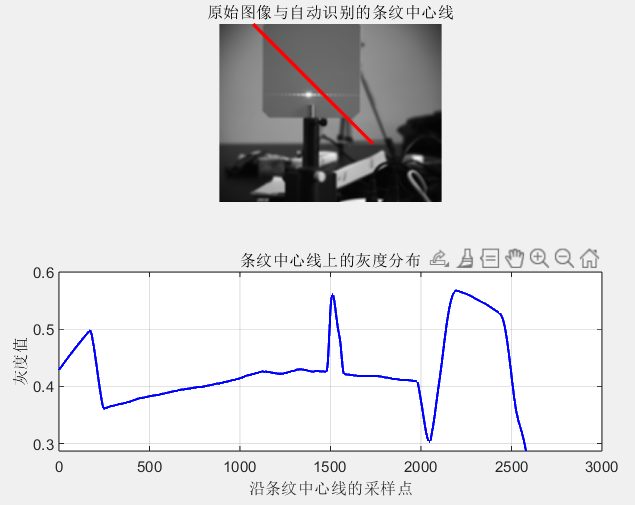
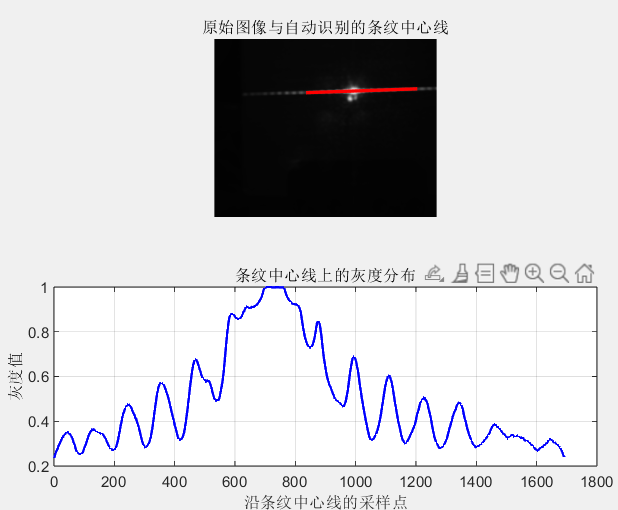
(二)待测细丝在激光束中并不处于中心位置,可能在与激光束垂直的平面内略有偏移
若细丝在与激光束垂直的平面内发生偏移,激光照射到细丝上的情况会发生改变。根据夫琅禾费衍射理论,光在遇到障碍物(细丝)时会发生衍射现象。当细丝不在激光束中心时,激光束照射到细丝的两侧光强分布会不一致,进而导致衍射条纹两侧的光强分布也不一致,表现为两侧条纹最小值不对称。例如,细丝偏向激光束的一侧,那么该侧的衍射光强会相对较弱,在条纹上就体现为该侧条纹的最小值可能更低。
(三)细丝并不与以激光束为法线的平面(即激光束的垂面),而是与之有一个倾斜角度
当细丝与激光束垂面存在倾斜角度时,激光在细丝上的衍射情况变得更为复杂。不同位置的激光与细丝的夹角不同,导致衍射光的传播方向和强度分布不均匀。在衍射屏上,这种不均匀性会使得两侧条纹的形成条件不同,从而出现两侧条纹最小值不对称的现象。例如,细丝一端与激光束垂面的夹角较小,另一端夹角较大,那么夹角小的一端衍射光相对更集中,而夹角大的一端衍射光相对更分散,反映在条纹上就是两侧条纹最小值存在差异。
大部分情况下,我们拍摄到的图片都或多或少地存在(二)、(三)这两种情况,因此分析这些情况对最后的测量误差的影响是极其必要的。
二、对条纹间距测算的影响分析
(一)绘制的扫描直线方向与条纹实际分布不重合
从理论上来说,只要扫描直线能穿越足够多的完整条纹,即使直线方向与条纹实际分布不重合,也不会影响条纹间距的测算。这是因为条纹间距本质上是条纹在空间上的周期性特征,在计算条纹间距时,我们通常是通过统计一定数量条纹的总宽度,再除以条纹数量来得到平均间距。只要扫描线能包含多个完整的条纹周期,不同位置穿越条纹的差异在平均计算过程中会被一定程度地抵消。但如果扫描直线与条纹分布夹角过大,可能会导致在统计条纹数量时出现误差,或者使得提取的条纹灰度信息不能准确反映条纹的真实周期性,从而对条纹间距测算产生一定影响。
上面是AI说的,但实际上,对于条纹和扫描线过于歪斜,我们测出来条纹间距实际上是真实间距在扫描线上的投影,这样会导致测量值略小于真实值。但因为算法可以保证绝对重合,因此这个不必担心。
(二)待测细丝在激光束中位置偏移
待测细丝在激光束中的位置偏移,虽然会导致条纹两侧光强分布不一致,但并不会改变条纹在空间上的周期性,即条纹间距在理论上保持不变。因为条纹间距主要取决于细丝的直径和激光的波长以及衍射屏到细丝的距离等因素,细丝在垂直于激光束平面内的位置偏移并没有改变这些关键参数。然而,实际测量中,由于两侧条纹光强差异,可能会对条纹位置的准确识别产生影响,从而间接影响条纹间距的测算。例如,在使用图像识别算法确定条纹中心位置时,光强较弱的一侧条纹可能会因为噪声等因素导致中心位置识别不准确,进而影响条纹间距的测量精度。
夫琅禾费衍射中,条纹间距的理论计算公式基于波动光学的原理推导得出。以单缝衍射(细丝衍射可类比单缝衍射模型,细丝相当于阻挡光传播的单缝)为例,暗纹间距=激光波长/细丝直径×衍射屏到细丝的距离。
由于决定条纹间距的这三个关键参数都不受细丝在垂直于激光束平面内位置偏移的影响,所以从理论上来说,哪怕细丝并没有在激光束的正中心,只要是距离固定了,条纹间距也是保持不变的。
光强差异对条纹间距测量精度影响的量化分析
在理想状况下,也就是没有噪声干扰,而且条纹两侧光强分布均匀时,借助图像识别算法能够精准识别出条纹的中心位置,此时测量得到的条纹间距记为\(\Delta x_{真}\)。
到了实际测量时,把条纹间距的测量值记作\(\Delta x_{测}\),条纹中心位置的识别误差用\(\Delta x_{中心}\)来表示。我们以相邻两条暗纹中心之间的距离作为条纹间距的衡量标准。假设在光强均匀的理想情形下,相邻两条暗纹中心的位置坐标分别是\(x_1\)和\(x_2\),那么理想的条纹间距\(\Delta x_{真}=x_2 - x_1\)。
但由于光强较弱的那一侧条纹受到噪声的影响,使得其中心位置的识别出现了误差。假设这一侧条纹的中心位置被错误地识别为\(x_2'\),那么实际测量得到的条纹间距\(\Delta x_{测}=x_2' - x_1\)。
这样一来,条纹间距的测量误差\(\Delta d = \Delta x_{测} - \Delta x_{真}=x_2' - x_2\),相对误差\(\delta = \frac{\Delta d}{\Delta x_{真}} \times 100\%=\frac{x_2' - x_2}{x_2 - x_1} \times 100\%\)。
从信号处理的角度进一步分析噪声对光强较弱一侧条纹中心位置识别的影响,我们可以假设条纹的灰度分布近似符合高斯分布。光强较弱的那一侧条纹,因为存在噪声,其灰度分布的信噪比(SNR)比较低。我们把噪声的标准差设为\(\sigma_{噪声}\),条纹灰度分布的标准差设为\(\sigma_{条纹}\),光强较弱一侧条纹中心位置的识别误差\(\Delta x_{中心}\)和信噪比是相关联的。一般而言,信噪比越低,图像识别算法错误判断条纹中心位置的可能性就越大。
要进一步明确\(\Delta x_{中心}\)和信噪比之间的具体关系,可以通过实验或者构建噪声模型的方式。比如,在特定的噪声水平下,多次重复测量光强较弱一侧条纹的中心位置,对测量得到的偏差分布情况进行统计,从而得到平均偏差值,将其作为\(\Delta x_{中心}\)的估计值,进而能够准确计算出这种情况对条纹间距测量精度产生的影响。
(三)细丝与激光束垂面存在倾斜角度
从理论角度,细丝与激光束垂面的倾斜角度并不会改变条纹的空间周期性,所以理论上不会影响条纹间距的测算。但实际上,倾斜角度会导致条纹的形状和光强分布发生变化,使得条纹边缘变得模糊,这会增加确定条纹准确位置的难度,进而影响条纹间距的测量。例如,在进行条纹间距计算时,需要准确找到条纹的峰值或谷值位置,而倾斜导致的条纹模糊可能会使这些位置的确定产生误差,从而影响条纹间距的测量结果。
解释得具体一点:
实际测量时,条纹的可识别性(而非 “理论存在性”)会因倾斜受到影响,具体体现在:
1. 条纹形状与光强分布的变化
当细丝倾斜时,激光照射到细丝上的 “有效衍射区域” 在空间上不再是对称的平面切割,而是倾斜的空间截段。这会导致:
- 衍射光的传播方向分布更分散,条纹不再是 “规则的平行亮暗带”,而是边缘出现渐变模糊(类似 “拖影”)。
- 条纹的光强分布从 “对称的高斯型” 变为非对称的渐变型,亮纹峰值和暗纹谷值的 “锐度” 下降。
2. 条纹位置识别的难度增加
测量条纹间距时,需要通过算法(或人工)识别亮纹峰值或暗纹谷值的位置。而倾斜导致的 “模糊边缘” 和 “非对称光强” 会带来两个问题:
- 峰值 / 谷值的 “定位锚点” 变弱:原本清晰的峰值(或谷值)因光强渐变变得 “平缓”,算法难以精准捕捉 “最亮 / 最暗” 的像素位置。
- 噪声干扰被放大:模糊区域的灰度变化与背景噪声更容易混淆,进一步增加了位置识别的误差。
这些误差会直接反映在 “条纹间距的测量值” 中 —— 即使理论间距不变,实际测量得到的间距会因 “位置识别不准” 而出现偏差。
“理论上倾斜不改变条纹周期性(间距理论值不变),但实际中倾斜导致测量误差(间距测量值不准)”,这一表述是严谨且符合实际的:
- 理论层面:核心衍射公式的参数不受垂直面倾斜的影响,因此 “理论间距” 恒定。
- 实际层面:倾斜改变了衍射光的传播与分布,使条纹变得模糊、光强非对称,增加了位置识别的难度,最终导致 “测量间距” 出现误差。
如果实验中需要高精度测量,必须尽量保证细丝与激光束垂面垂直,以减少这种 “理论与实际” 的偏差。
三、对细丝直径测算的影响分析
AI说得太多我就给删了。总之,细丝直径是直接用△x得到的,所以对△x获取有影响的,对细丝直径就有一样的影响。
四、误差计算与分析
(一)扫描直线方向偏差带来的误差
当扫描直线存在倾斜(与条纹实际分布方向夹角为\(\theta\))时,像素级定位误差会因 “投影效应” 而被放大,最终影响条纹间距乃至细丝直径的测量精度。以下从误差来源、量化计算和影响分析三个方面展开详细分析:
①像素级定位误差的来源
在图像中识别条纹中心(亮纹峰值或暗纹谷值)时,像素级误差主要源于两方面:
- 图像本身的离散性:CCD 图像由离散像素组成,条纹的 “连续光强分布” 会被 “像素化”。例如,一条亮纹的峰值可能处于两个像素之间,算法只能近似取最亮的像素位置,存在亚像素级误差(通常小于 1 个像素)。
- 算法的近似性:即使使用高精度的中心定位算法(如高斯拟合、重心法),也会因 “光强分布的非理想性”(如噪声、光强不均匀)产生算法拟合误差(通常在 1 个像素以内)。
②倾斜对像素级误差的放大作用
假设条纹实际方向为水平,扫描直线与水平方向夹角为\(\theta\),此时:


三、量化分析(以 1 个像素误差为例)
已知 CCD 像素尺寸——
一个像元的尺寸为s=3.45μm,因此对于能够完全保证提取到亮度中心的代码,可以计算误差如下——

而对于正常的人眼观测和固定误差,θ角不会超过5°,代入算出来,最后的细丝宽度的误差△a不超过2.19nm.
(二)细丝位置偏移带来的误差
要通过激光束的光束横截面直径定量分析细丝位置偏移带来的误差,需结合激光束的光强分布(通常为高斯分布)和细丝在光束中的偏移对衍射光强的影响展开,步骤如下:
①激光束的高斯分布模型
氦氖激光的横模为TEM00,其光强在横截面沿径向呈高斯分布,表达式为:![]()
其中:
- I_0为光束中心 r=0 的光强;
- r为到光束中心的径向距离;
- w为光束半径(光强降为中心1/e^2时的半径)。
②细丝位置偏移的影响
设激光束横截面直径为D,若细丝在垂直于激光束的平面内偏移,偏移量为△r(即细丝中心与激光束中心的距离为△r,则:
1. 光强分布的非对称性
细丝衍射的光强由 “照射到细丝上的激光光强” 决定。由于激光光强是高斯分布,偏移后:
- 细丝靠近光束中心的一侧,光强更强(I更大);
- 远离中心的一侧,光强更弱(I更小)。
这种光强非对称性会导致衍射条纹的光强分布也出现非对称:亮纹峰值和暗纹谷值的光强不再左右均匀,进而影响条纹位置的识别精度。
2. 条纹间距测量的绝对误差△d
光强的非对称性会使 “条纹中心位置的识别误差” 与光强分布相关。结合高斯分布的光强梯度,偏移量δr与光强变化的关系可近似为:
![]()
而条纹位置识别的误差(即绝对误差△d与光强变化的相对误差成正比(光强越不均匀,识别误差越大),因此:![]() (d为无偏移时的条纹间距)。
(d为无偏移时的条纹间距)。
代入光强变化的近似式,可得: ![]()
③相对误差的计算

因为光强不均匀导致的条纹识别位置的误差并不容易量化定性,因此可能在具体实验之前的无法得出切实数据,只能得到如下结论:
细丝位置偏移带来的相对误差与激光束的光束半径和偏移量直接相关:
- 偏移量△r越大,光强分布的非对称性越强,相对误差越大;
- 激光束半径w越小(光束越 “细”),相同偏移量下,光强变化越显著,相对误差也越大。
若要减小该误差,需尽量将细丝置于激光束中心,此时光强分布对称,条纹识别误差最小。
(三)细丝倾斜角度带来的误差
细丝倾斜角度带来的误差主要源于条纹模糊导致的条纹间距测量误差,其误差计算方式与细丝位置偏移带来的误差类似,不再赘述。
五、结论
夫琅禾费衍射条纹两侧最小值不对称可能是由绘制的扫描直线方向与条纹实际分布不重合、待测细丝在激光束中位置偏移以及细丝与激光束垂面存在倾斜角度等原因导致。从理论上来说,这些情况本身并不会改变条纹间距的理论值,因此也不会直接影响细丝直径的测算。但在实际测量过程中,这些情况会影响条纹间距测量的准确性,进而对细丝直径的测算结果产生误差。为了减小误差,在实验中应尽量保证绘制的扫描直线方向与条纹实际分布重合、将待测细丝放置在激光束中心位置且与激光束垂面垂直,同时采用更精确的图像识别算法来提高条纹位置识别的准确性。
