【数据结构---并查集】（并查集的原理，实现与应用）

一.并查集的原理

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-findset)

例如：有十个小朋友，他们两两之间可能存在直接的朋友关系，现在需要判断其中任意两个人是否是朋友（因为朋友的朋友也是朋友，所以不一定是直接的朋友关系）
现给这些小朋友进行编号：{0, 1, 2, 3,4, 5, 6, 7, 8, 9};给以下数组用来存储该小集体

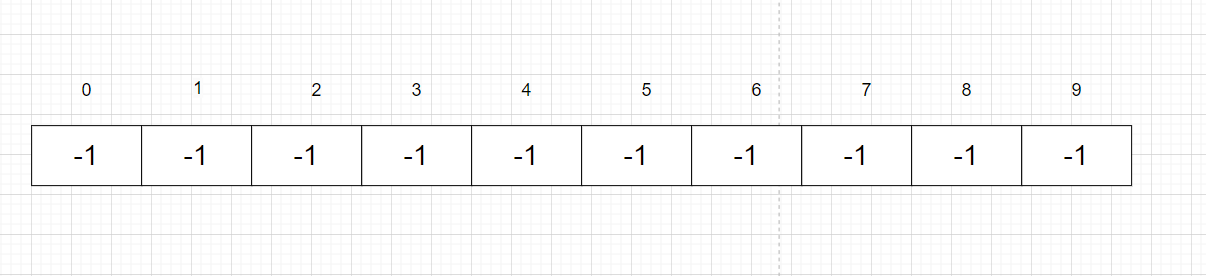
集合的树形表示：

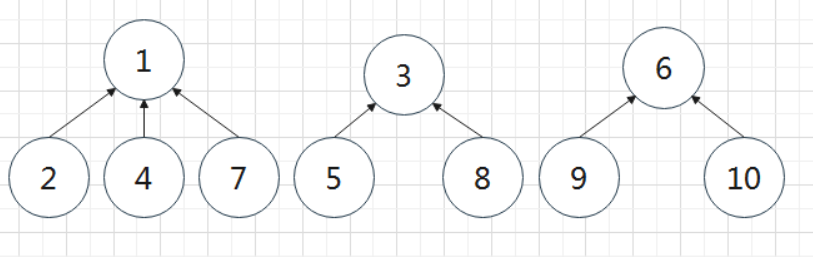
从图中可以看出1，2，4，7是一组朋友，3，5，8是第二组，6，9，10是第三组，因此我们可以这样表示这些集合：

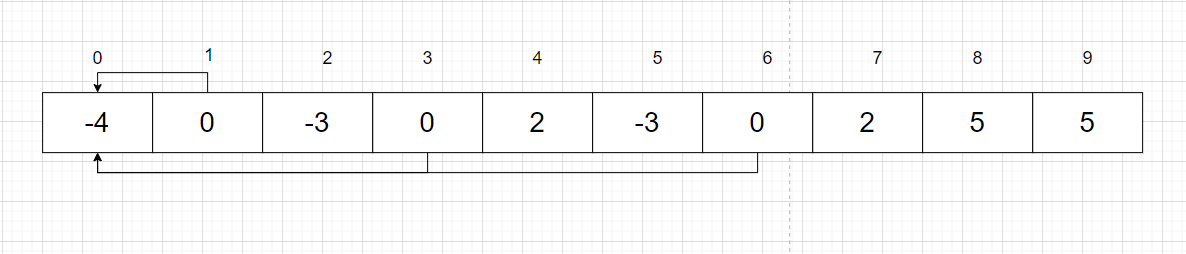
如果数组中的值为-1，表示这个节点就是这个集合的根，大于0则指向他的父节点。

通过上面这个例子，可以看出并查集适合解决这些问题：

1. 查找元素属于哪个集合
   沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置)
2. 查看元素是否属于同一集合
   沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在
3. 将两个集合合并
   找到两个集合的根，将其中一个根节点的父节点改为另一个根节点。
4. 集合的个数
   遍历数组，数组中元素为负数的个数即为集合的个数。

二.并查集的实现

#include <iostream>
#include <vector>template <class T>
class UnionFindSet
{
public:UnionFindSet(size_t n): _ufs(n, -1){}// 查找index在哪个集合中void FindRoot(int index){int root = index;while(_ufs[root] >= 0){root = _ufs[root];}return root;}// 合并两个集合bool Union(int x,int y){int root1 = FindRoot(x);int root2 = FindRoot(y);if(root1 == root2)return false;_ufs[root1] += _ufs[root2];_ufs[root2] = root1;return true;}// 获取集合个数size_t Count(){size_t cnt = 0;for(auto &e : _ufs){if(e < 0){++cnt;}}return cnt;}private:std::vector<int> _ufs;
};

三.并查集的应用

1.省份数量

链接: 力扣

int FindRoot(vector<int>& ufs,int x)
{int root = x;while(ufs[root] >= 0){root = ufs[root];}return root;
}class Solution {
public:int findCircleNum(vector<vector<int>>& isConnected) {int n = isConnected.size();vector<int> ufs(n,-1);for(int i = 0;i < n;i++){for(int j = 0;j < n;j++){if(isConnected[i][j] == 1){int root1 = FindRoot(ufs,i);int root2 = FindRoot(ufs,j);if(root1 == root2){continue;}ufs[root1] += ufs[root2];ufs[root2] = root1;}}}int n = 0;for(auto &e:ufs){if(e < 0){++n;}}return n;}   
};

2. 等式方程的可满足性

链接: 力扣

class Solution {
public:bool equationsPossible(vector<string>& equations) {int n = equations.size();vector<int> ufs(26, -1);auto findRoot = [&ufs](int x) -> int {while (ufs[x] >= 0) {x = ufs[x];}return x;};for (int i = 0; i < n; i++) {if (equations[i][1] == '=') {int root1 = findRoot(equations[i][0] - 'a');int root2 = findRoot(equations[i][3] - 'a');if (root1 != root2) {ufs[root2] = root1;}}}for (int i = 0; i < n; i++) {if (equations[i][1] == '!') {int root1 = findRoot(equations[i][0] - 'a');int root2 = findRoot(equations[i][3] - 'a');if (root1 == root2) {return false;}}}return true;}
};