两数的乘积 = 最大公约数 × 最小公倍数

证明思路

我们可以通过对两个数进行质因数分解，从数学原理上推导证明“两数的乘积等于它们的最大公约数与最小公倍数的乘积”这一结论。

具体证明过程

设两个正整数为 (a) 和 (b)，将它们进行质因数分解：

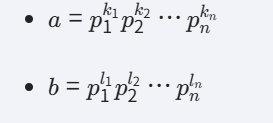
1. 求最大公约数（GCD）

最大公约数是两个数公有的质因数的乘积，且每个质因数的指数取两个数中该质因数指数的最小值。即：

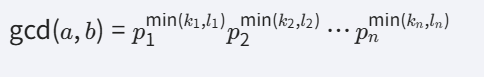
2. 求最小公倍数（LCM）

最小公倍数是包含两个数所有质因数的乘积，且每个质因数的指数取两个数中该质因数指数的最大值。即：

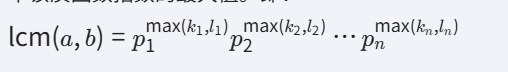
3. 计算最大公约数与最小公倍数的乘积

4. 计算两数的乘积

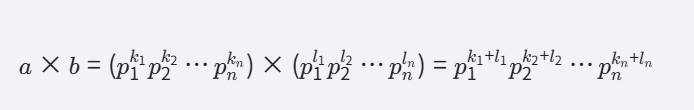
结论

通过以上推导可知，两数的乘积等于它们的最大公约数与最小公倍数的乘积。

示例验证

可以看到，两数的乘积确实等于它们的最大公约数与最小公倍数的乘积。