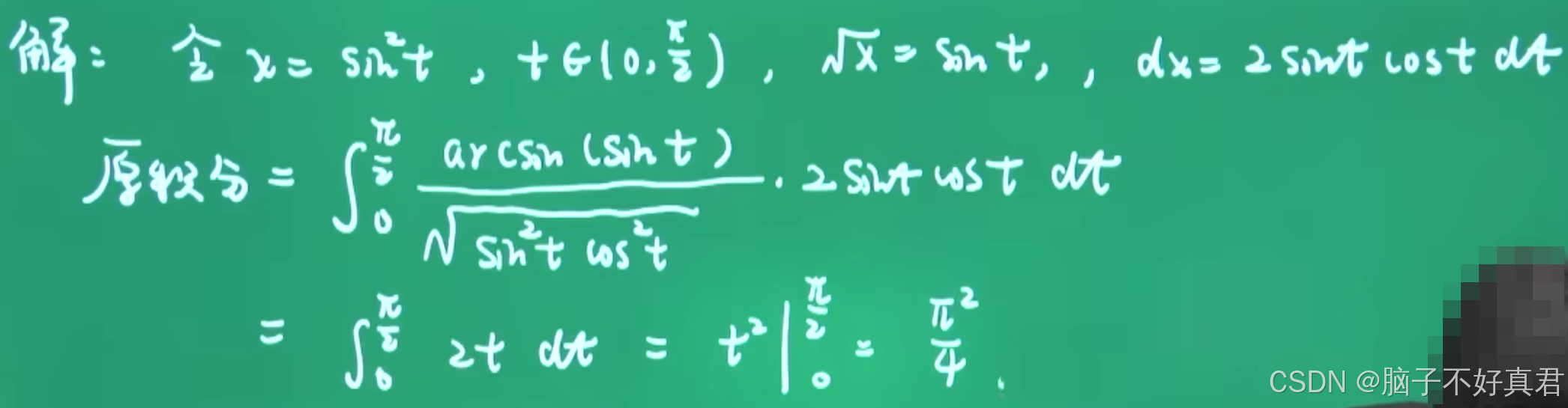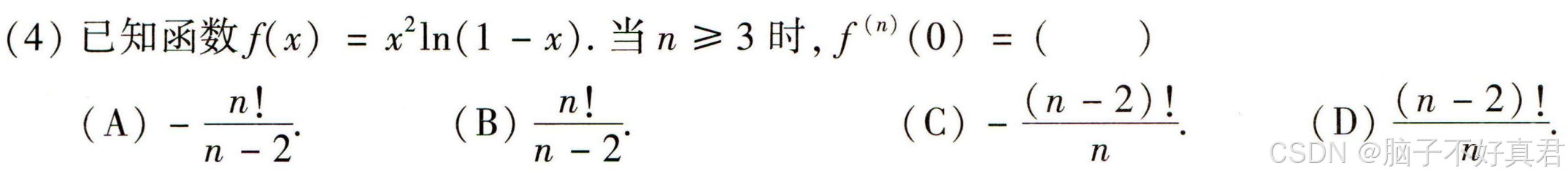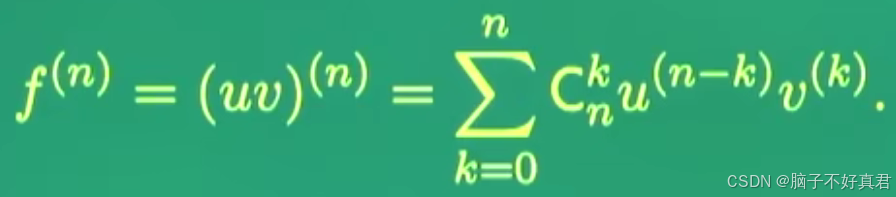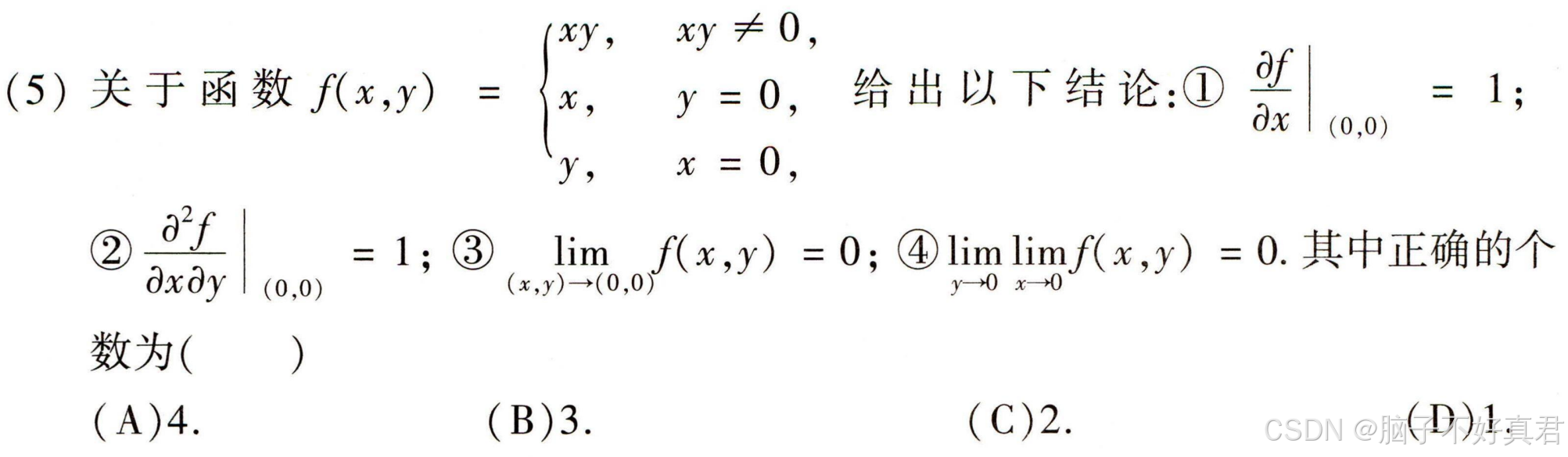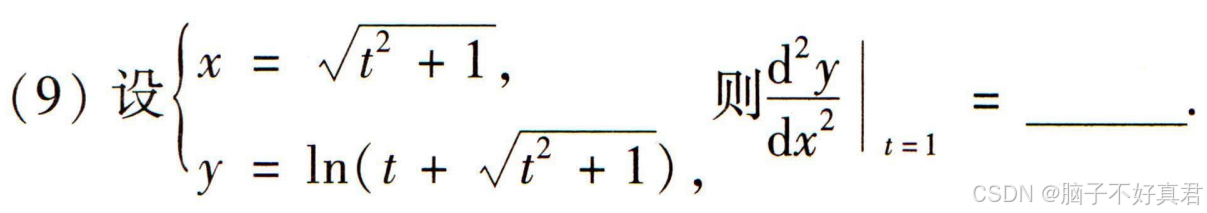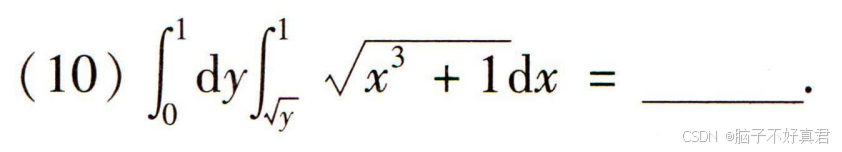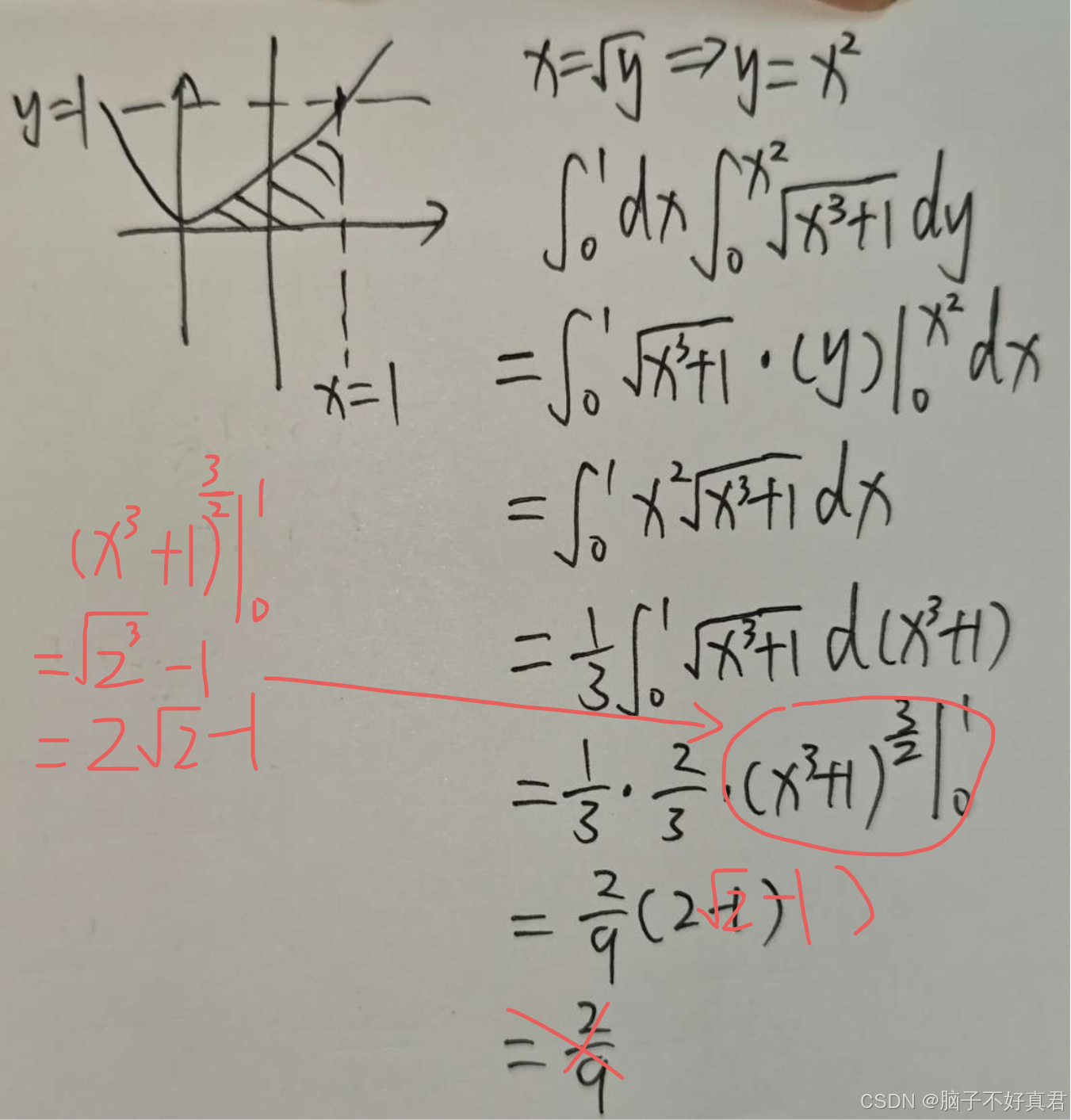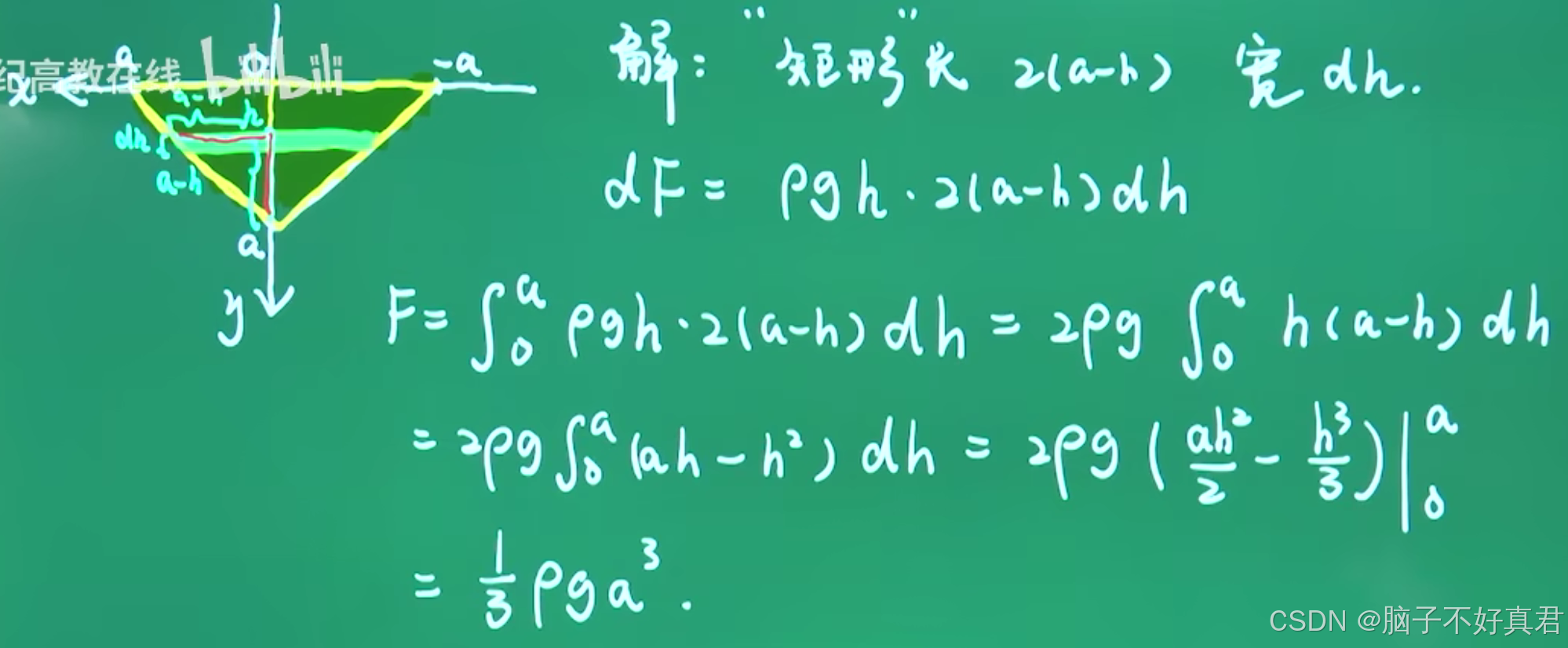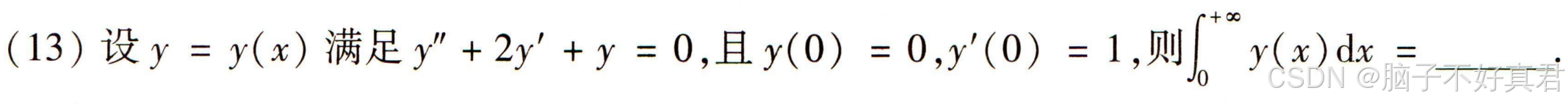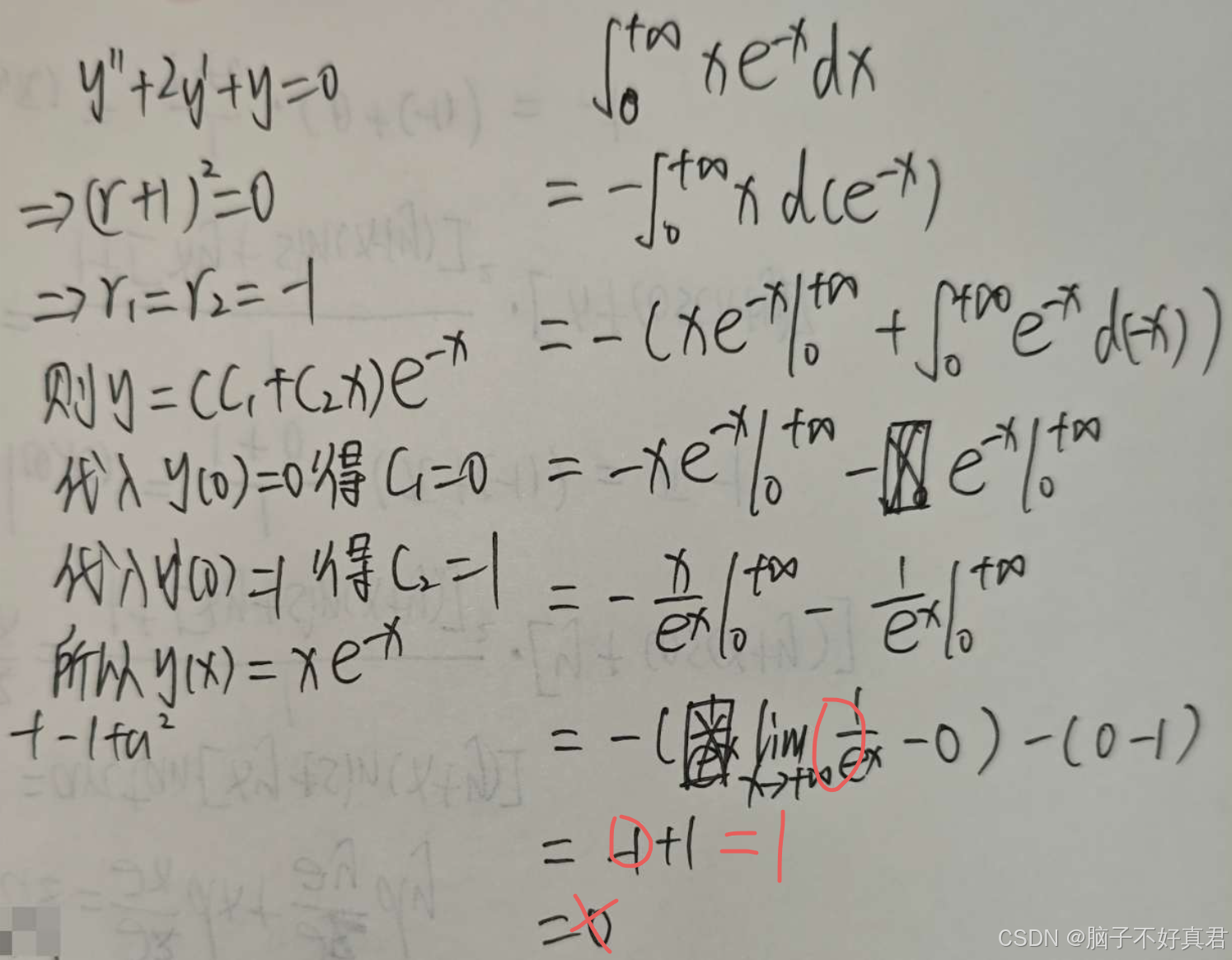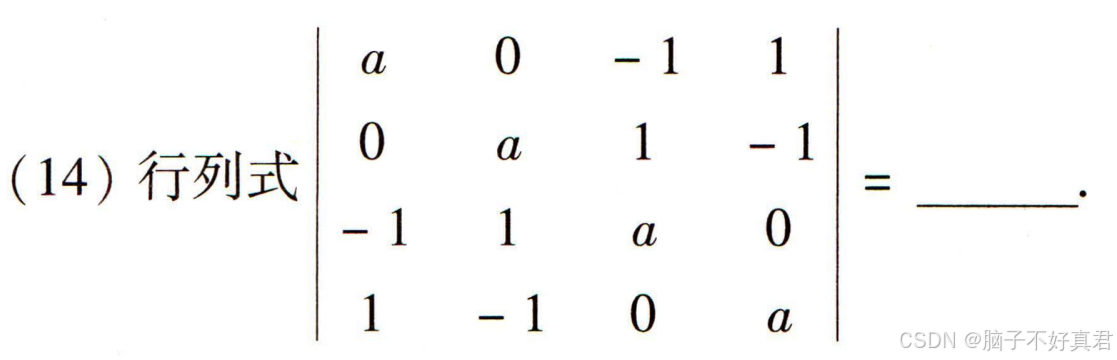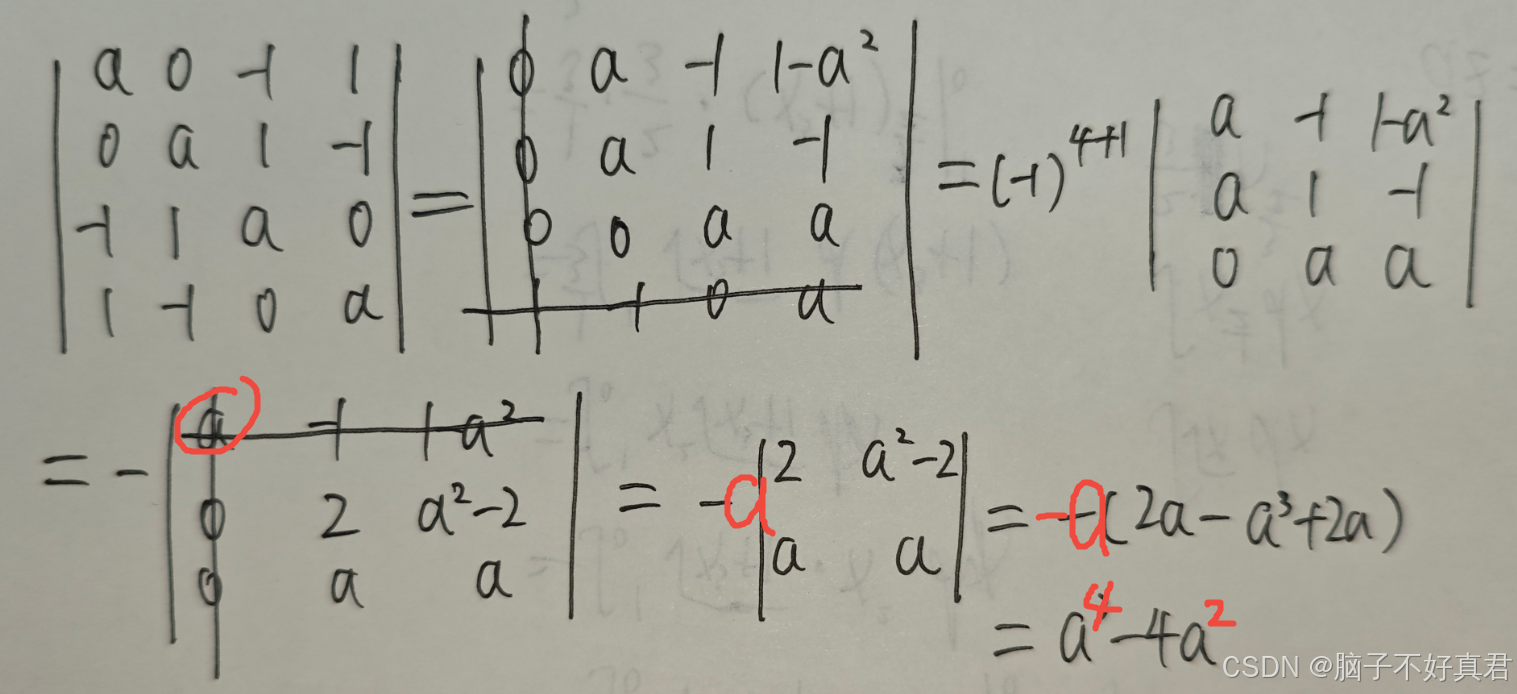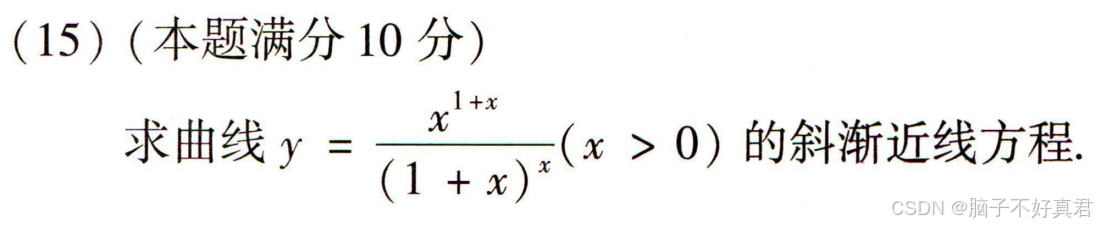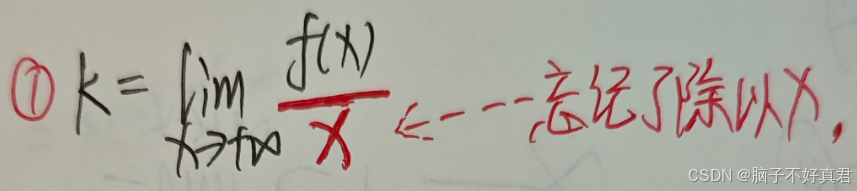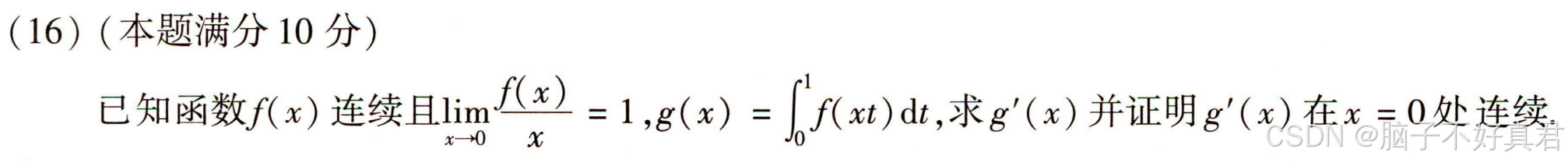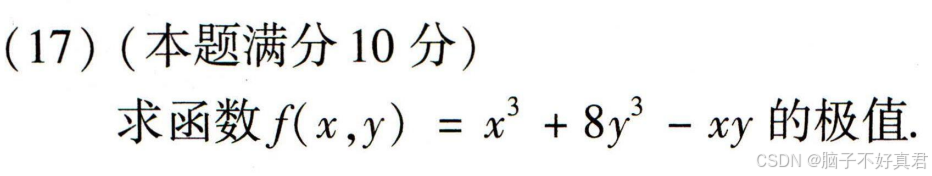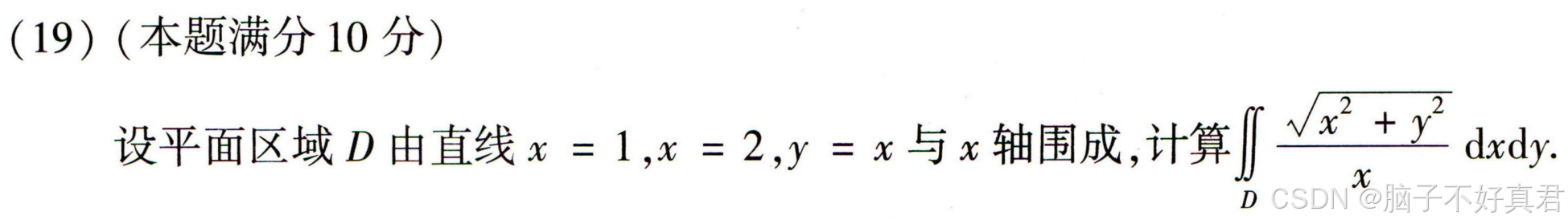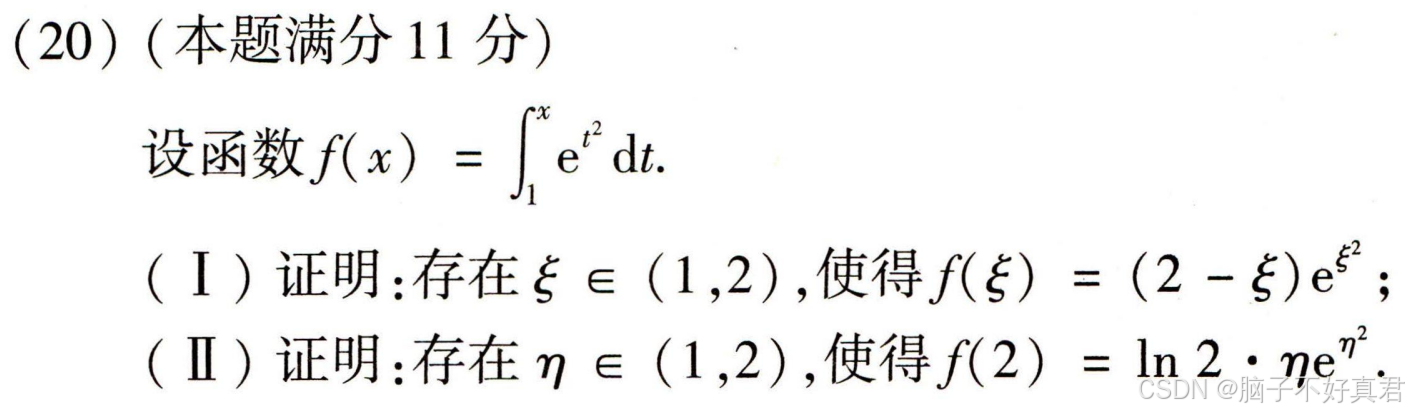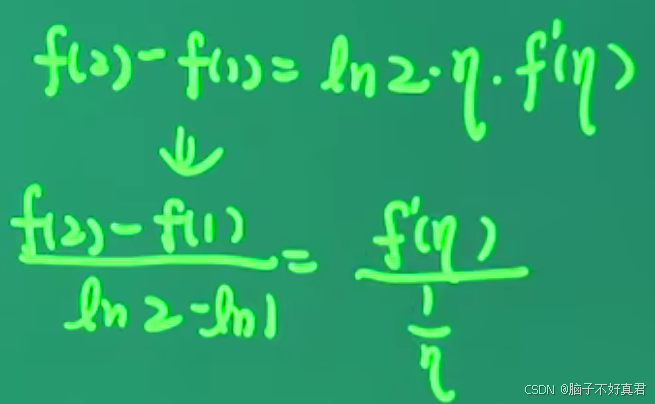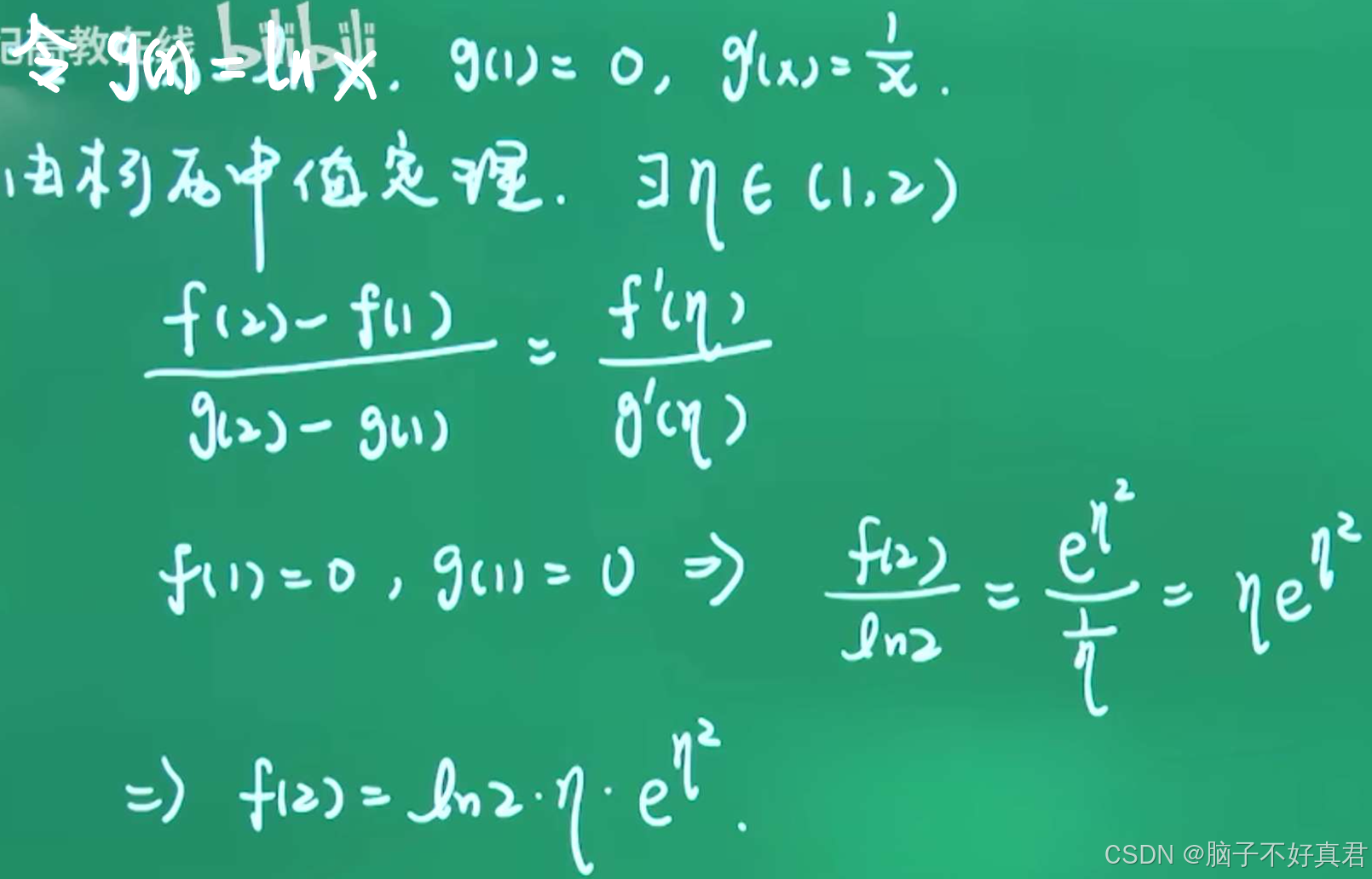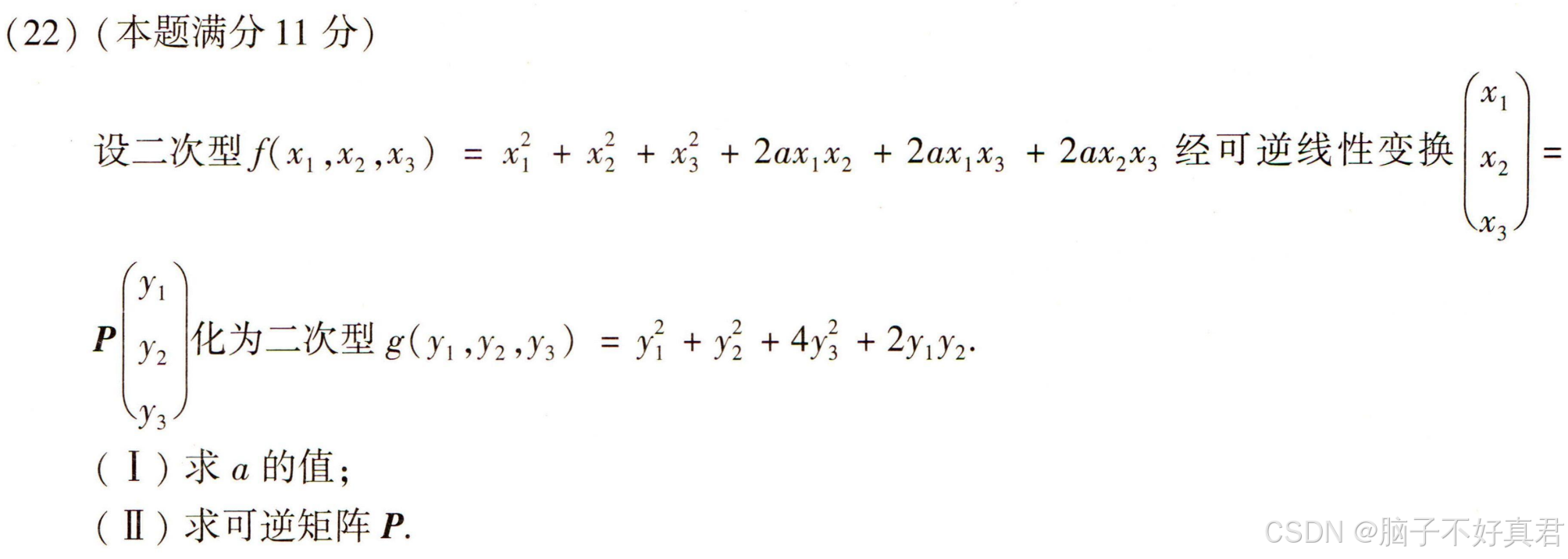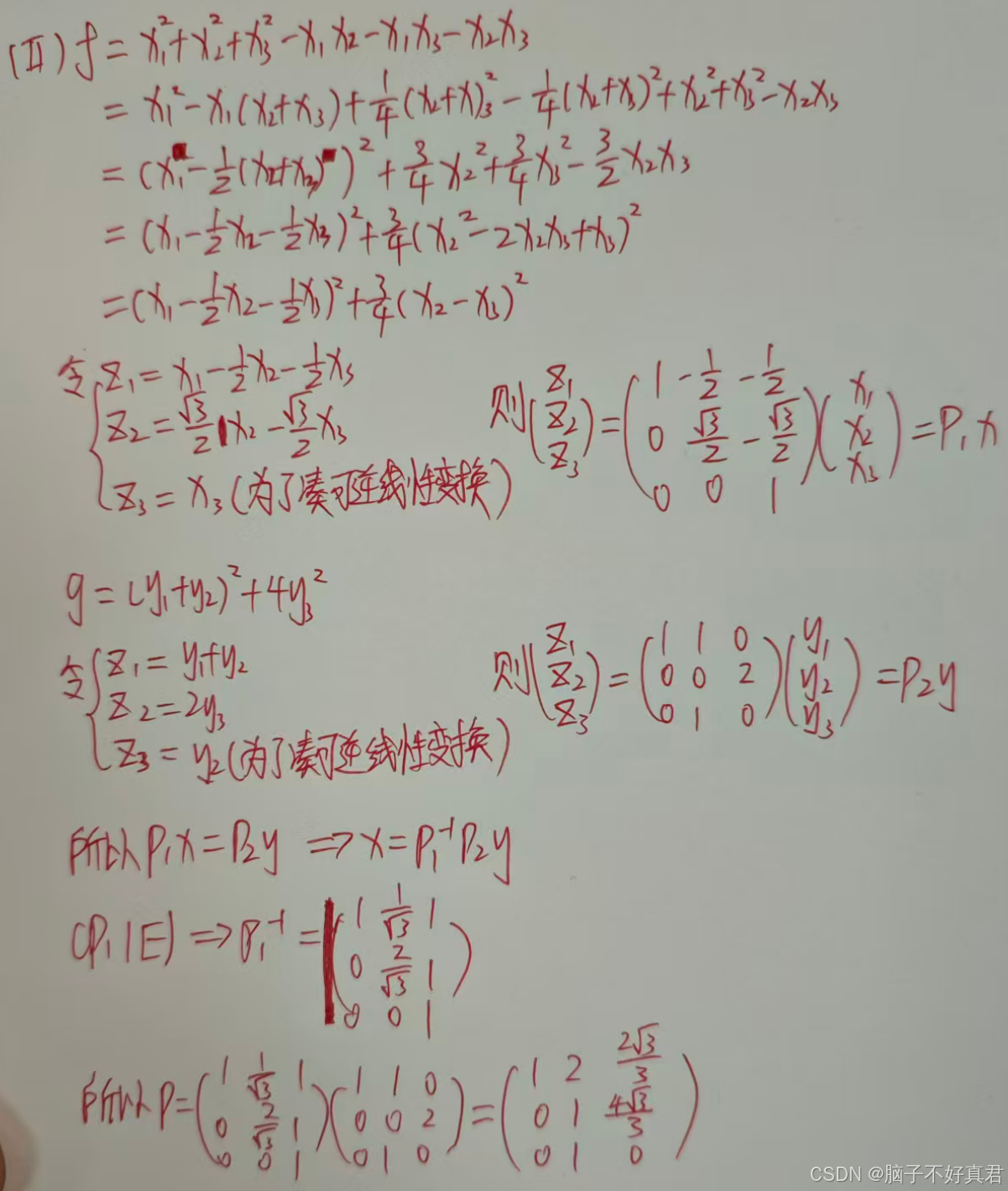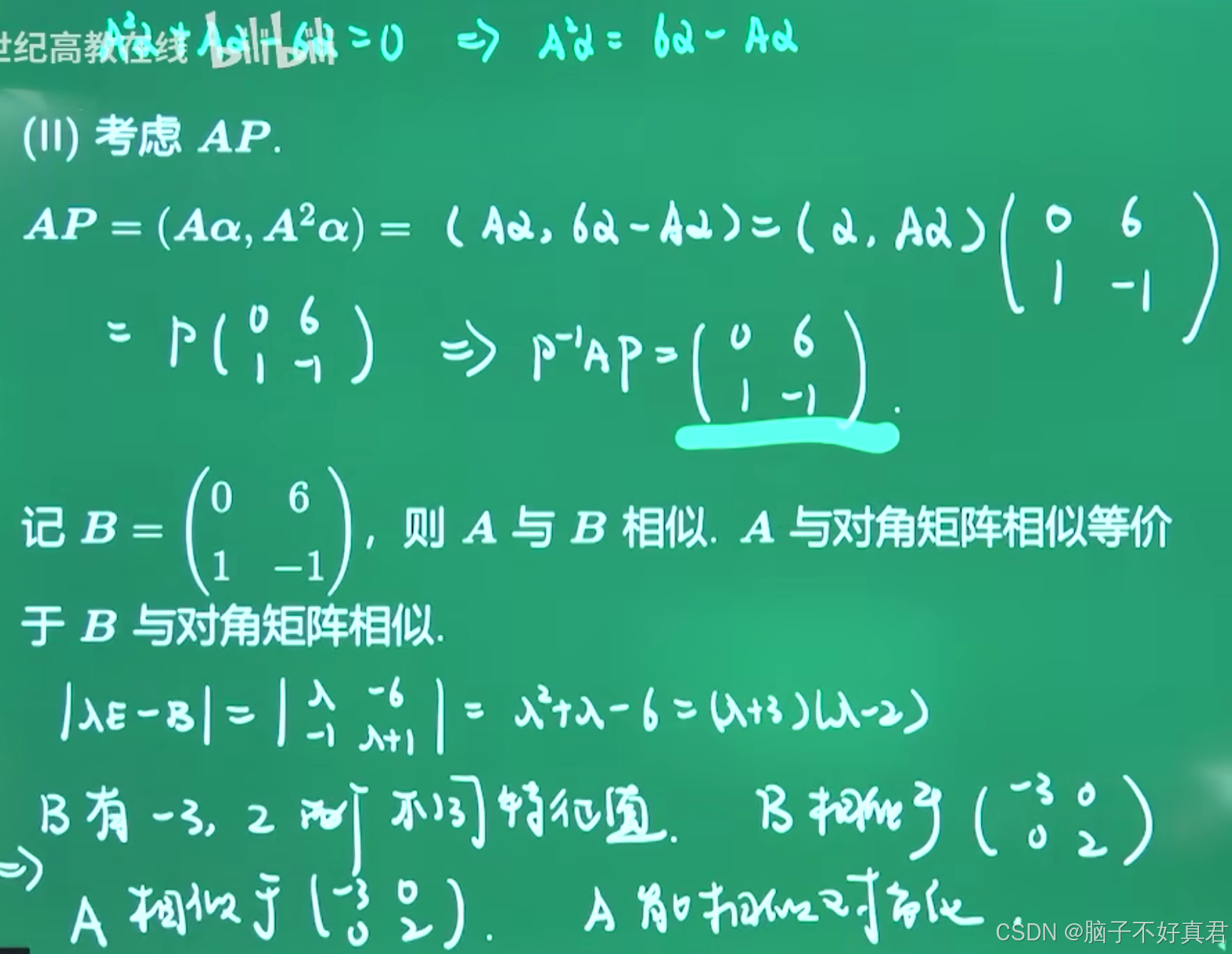2020考研数学(二)真题
一、选择题
★新题型(1)
考点:
先求出 被积函数在 t→0 时的麦克劳林展开 和 积分上下限x→0的麦克劳林展开,再像普通定积分那样计算即可
第一类间断点(可去;连续)
第二类间断点(无穷;振荡)
(2)
(3)
方法一(根号换元法)
方法二(三角换元法)
★有未记住公式(4)
方法一(逐项求导+代入选项)
方法二(莱布尼茨公式+逐项求导)
(5)
考点:
一阶偏导的定义式;
二阶偏导的定义式;
二重极限的计算方法;
累次极限的计算方法
题型名称:抽象函数的问题(举特例)(6)
方法一:举特例
★(记住这个构造的辅助函数)方法二:构造辅助函数证明
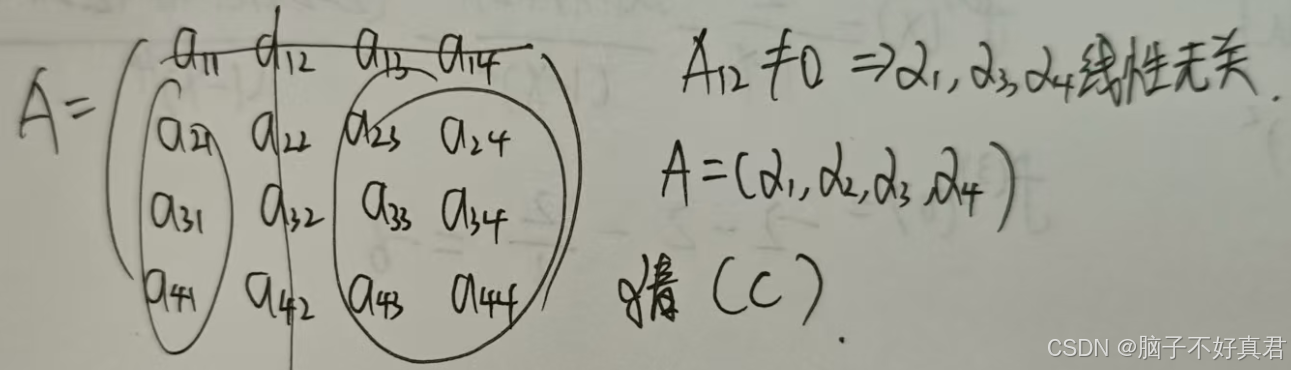
★不会的题(7)
考点:
A 不可逆 ⇔ |A|=0;
如果一个向量组的部分分量组成的向量组是线性无关的,那么原向量组也一定是线性无关的;
r(A) 与 r(A*) 的关系;
A*A=|A|E ⇒ A*的解;
结论:低维无关 ⇒ 高维无关,高维相关 ⇒ 低维相关
★有记混淆点(8)
易混淆点:
相同特征值对应的特征向量的线性组合仍是矩阵的特征向量;不同特征值对应的特征向量的线性组合仍不是矩阵的特征向量;
★结论:矩阵 P的列向量应为 A的线性无关的特征向量,且排列顺序与目标对角矩阵的特征值顺序一致
方法一:利用结论相同特征值对应的特征向量的线性组合仍是矩阵的特征向量
方法二:严格说明
二、填空题
(9)
错误点:
没有通分
(10)
错误点:
看漏了次幂
(11)
(12)
(13)
错误点:
脑子短路了?
(14)
错误点:
脑子短路了
三、解答题
★反正就是很重要(15)
错因:
★(16)
注意点:
①对u=xt进行换元后不用考虑处理g(x)中x为u/t;
②分段讨论函数的思路;
③用导数的定义式求x≠0处;
(17)
★(18)
考点:
换元法构造两个方程求 f(x) 表达式;微元法理解旋转体体积计算公式;
对y积分时函数要化为x=(含y的函数表达式);
三角换元法计算积分;
★(19)
(20)
考点:
对要证等式移项,转化为根/零点问题;
对要证等式移项并且添加结果为0项,观察接近于哪个定理;
(Ⅰ)
(Ⅱ)
(21)
(22)
考点:
合同矩阵的秩相同;
配方法化二次型为规范形;
二次型 f(x) 和 g(y) 对应的矩阵 A 和 B 是合同的,这意味着存在两个不同的可逆变换(我们称之为 P1 和 P2),可以将这两个二次型化为同一个规范形;
(Ⅰ)
(Ⅱ)
(23)
考点:
反证法;
列向量线性无关⇔矩阵可逆;
线性相关和线性无关的定义;
特征值不同⇒不同特征值对应的特征向量必然是线性无关的⇒一个 n 阶矩阵若有 n 个不同的特征值,则它一定可以被对角化;
(Ⅰ)
(Ⅱ)