北航计算机保研机试题+解答

北航计院每年都是两/三道题，大模拟，考查各种数据结构（尤其是树和链表）的使用。

参考资料：GitHub - Muyiyunzi/BUAA-CS-Codes: 北京航空航天大学计算机学院研究生考试复试上机部分往年试题及解答

2021：

第一题：

在操作系统中，空闲存储空间通常以空闲块链表组织，每个块包含块起始位置、块长

度及一个指向下一块的指针。空闲块按照存储位置升序组织，最后一块指向第一块（循环

链表）。当有空间申请请求时，按照如下原则在空闲块循环链表中寻找并分配空闲块：

1）从当前位置开始遍历空闲块链表（初始是从地址最小的第一个空闲块开始），寻找

满足条件的最小块（即：大于等于请求空间的最小空闲块，如果有多个大小相同的最小空

闲块，则选择遍历遇到的第一个空闲块）（最佳适应原则）；

2）如果选择的空闲块恰好与请求的大小相符合，则将它从链表中移除并返回给用户；

这时当前位置变为移除的空闲块指向的下一空闲块；

3）如果选择的空闲块大于所申请的空间大小，则将大小合适的空闲块返回给用户，剩

下的部分留在空闲块链表中；这时当前位置仍然为该空闲块；

4）如果找不到足够大的空闲块，则申请失败；这时当前位置不变。

例如：下图示例给出了空闲块链表的初始状态，每个结点表示一个空闲块，结点中上

面的数字指空闲块的起始位置，下面的数字指空闲块的长度，位置和长度都用正整数表

示，大小不超过 int 表示范围。当前位置为最小地址为 1024 的空闲块。

若有 4 个申请空间请求，申请的空间大小依次为：1024、2560、10240 和 512。则从当

前位置开始遍历上图的链表，按照上述原则寻找到满足条件的最小块为地址是 16384 的空

闲块，其长度正好为 1024，所以将其从链表中删除，这时链表状态如下图所示，当前位置

变成地址为 32768 的空闲块.

从当前位置开始为第二个空间请求（大小为 2560）遍历链表，按照上述原则寻找到满

足条件的最小块为地址是 80896 的空闲块，其长度为 3072，大于请求的空间大小，于是申

请空间后该空闲块剩余的长度为 512，当前位置为地址是 80896 的空闲块，链表状态如下

图所示：

从当前位置开始为第三个空间请求（大小为 10240）遍历链表，遍历一圈后发现找不

到足够大的空闲块，则忽略该请求，当前位置不变。下面继续为第四个空间请求（大小为

512）遍历链表，按照上述原则寻找到满足条件的最小块为当前位置的空闲块，其长度等于

请求的空间大小，于是将该空闲块删除后，链表状态变为下图所示：

编写程序，模拟上述空闲空间申请。

测试用例 1：

输入：

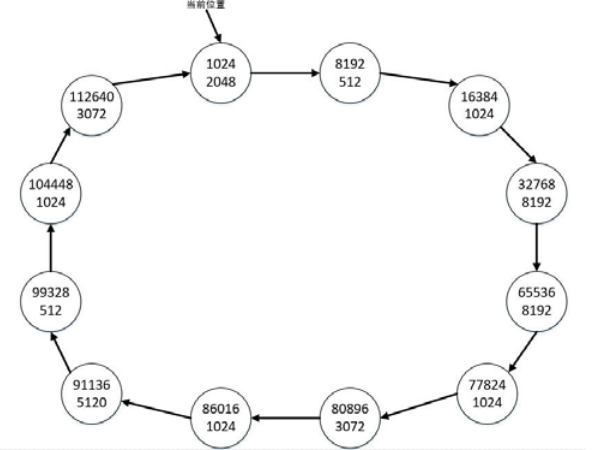
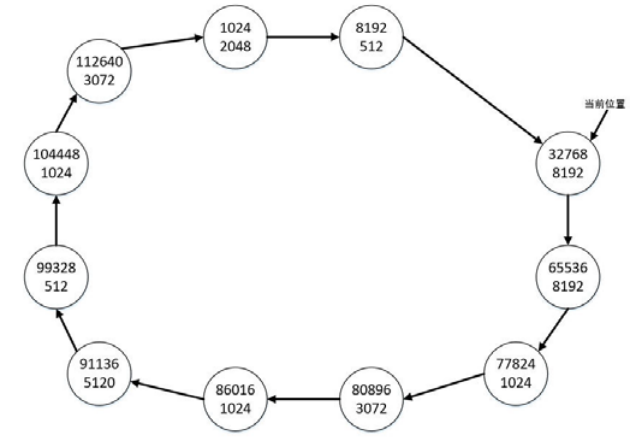
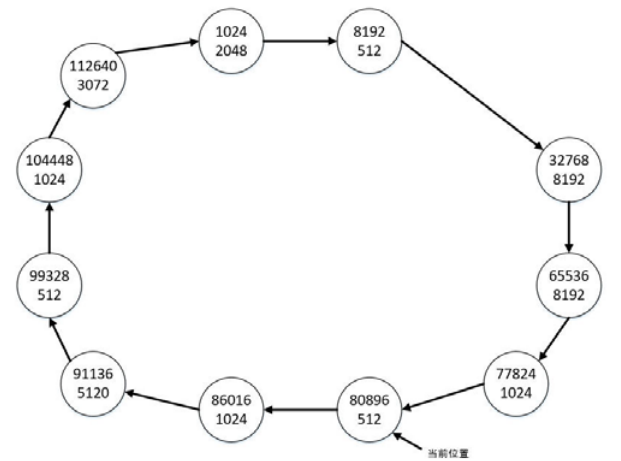
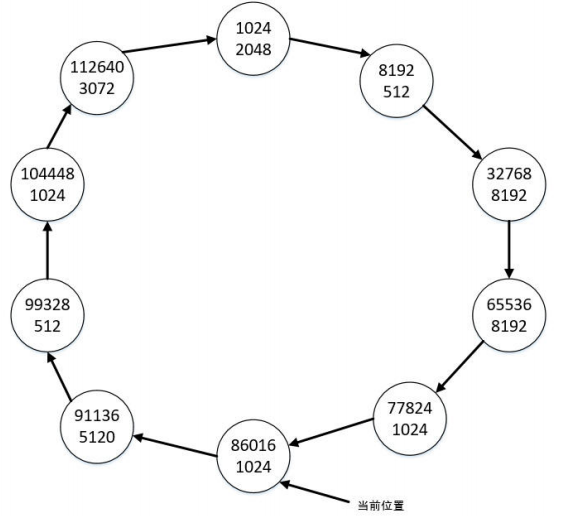
12
1024 2048
8192 512
16384 1024
32768 8192
65536 8192
77824 1024
80896 3072
86016 1024
91136 5120
99328 512
104448 1024
112640 3072
1024 2560 10240 512 1024 6400 512 -1

输出：

104448 1024
112640 3072
1024 2048
8192 512
32768 1792
65536 8192
77824 1024
91136 5120

样例说明：

样例输入了 12 个空闲块的信息，形成了如上述第一个图所示的空闲块链表；然后读取

了 7 个空间申请请求，为前 4 个申请请求分配空间后，空闲块链表状态为上述最后一张图

所示。满足第五个请求后，将删除地址为 86016 的空闲块；满足第六个请求后，地址为

32768 的空闲块剩余长度为 1792；满足第七个请求后，将删除地址为 99328 的空闲块，这

时链表中剩余 8 个空闲块，当前位置为地址是 104448 的空闲块，从该空闲块开始依次遍历

输出所有剩余空闲块的起始位置和长度。

本题考查循环链表，有几个tips：

第一个是注意do-while使用，先do，然后再判断while，所以再最后输出的时候，当p为倒数第二个时，他输出完，p=p->next，此时进入while判断就出去了，换而言之，漏了最后一个的打印，所以要补上。

第二个是注意最佳适应的实现。我采取的做法是统一绕一圈并用特定元素记录最值，绕完之后再把p重置到给定位置。

#include <bits/stdc++.h>
using namespace std;
int n;
struct Node
{int sta;int capa;Node *pre = nullptr;Node *next = nullptr;Node(int sta, int capa) : sta(sta), capa(capa) {}
};int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n;int a, b;Node *head = nullptr;Node *cur;for (int i = 0; i < n; i++){cin >> a >> b;if (head == nullptr){head = new Node(a, b);head->next = head;head->pre = head;cur = head;}else{Node *p = new Node(a, b);// 尾插法p->pre = cur;p->next = head;head->pre = p;cur->next = p;cur = p;}}int require;Node *p = head;while (cin >> require && require != -1){int tempmin = INT_MAX;Node *t = head;Node *x = p->pre;do{if (p->capa >= require){if (p->capa < tempmin){tempmin = p->capa;t = p;}}p = p->next;} while (p != x);if (tempmin == INT_MAX){p = p->next;continue;}else if (tempmin == require){Node *z = t->next;Node *y = t->pre;y->next = z;z->pre = y;p = z;delete (t);}else if (tempmin > require){p = t;p->capa -= require;}}Node *x = p->pre;do{cout << p->sta << " " << p->capa << endl;p = p->next;} while (p != x);cout << p->sta << " " << p->capa << endl;return 0;
}

第二题：

假设某机场所有登机口（Gate）呈树形排列（树的度为 3），安检处为树的根，如下图

所示。图中的分叉结点（编号>=100）表示分叉路口，登机口用小于 100 的编号表示（其

一定是叶结点）。通过对机场所有出发航班的日志分析，得知每个登机口每天的平均发送旅

客流量。作为提升机场服务水平的一个措施，在不改变所有航班相对关系的情况下（出发

时间不变，原在同一登机口的航班不变），仅改变登机口（如将 3 号登机口改到 5 号），使

得整体旅客到登机口的时间有所减少（即从安检口到登机口所经过的分叉路口最少）。

编写程序模拟上述登机口的调整，登机口调整规则如下：

1）首先按照由大到小的顺序对输入的登机口流量进行排序，流量相同的按照登机口编

号由小到大排序；

2）从上述登机口树的树根开始，按照从上到下（安检口在最上方）、从左到右的顺

序，依次放置上面排序后的登机口。

例如上图的树中，若只考虑登机口，则从上到下有三层，第一层从左到右的顺序为：

5、6、14、13，第二层从左到右的顺序为：7、8、9、10、1、2、18、17、16、15，第三层

从左到右的顺序为：11、12、3、4、20、19。若按规则 1 排序后流量由大至小的前五个登

机口为 3、12、16、20、15，则将流量最大的 3 号登机口调整到最上层且最左边的位置

（即：5 号登机口的位置），12 号调整到 6 号，16 号调整到 14 号，20 号调整到 13 号，15

号调整到第二层最左边的位置（即 7 号登机口的位置）。

输入形式：

1）首先输入一个整数表示树结点关系的条目数，接着在下一行开始，按层次从根开始

依次输入树结点之间的关系。其中分叉结点编号从数字 100 开始（树根结点编号为 100，

其它分叉结点编号没有规律但不会重复），登机口为编号小于 100 的数字（编号没有规律但

不会重复，其一定是一个叶结点）。树中结点间关系用下面方式描述：

R S1 S2 S3

其中 R 为分叉结点，从左至右 S1，S2，S3 分别为树叉 R 的子结点，其可为树叉或登

机口，由于树的度为 3，S1，S2，S3 中至多可以 2 个为空，该项为空时用-1 表示。各项间

以一个空格分隔，最后有一个回车。如：

100 101 102 103

表明编号 100 的树根有三个子叉，编号分别为 101、102 和 103，又如：

104 7 8 -1

表明树叉 104 上有 2 个编号分别为 7 和 8 的登机口。

假设分叉结点数不超过 100 个。分叉结点输入的顺序不确定，但可以确定：输入某个

分叉结点信息时，其父结点的信息已经输入。

2）在输入完树结点关系后，接下来输入登机口的流量信息，每个登机口流量信息分占

一行，分别包括登机口编号（1~99 之间的整数）和流量（大于 0 的整数），两整数间以一

个空格分隔。

输出形式：

按照上述调整规则中排序后的顺序（即按旅客流量由大到小，流量相同的按照登机口

编号由小到大）依次分行输出每个登机口的调整结果：先输出调整前的登机口编号，再输

出要调整到的登机口编号。编号间均以一个空格分隔。

输入：

12
100 101 102 103
103 14 108 13
101 5 104 6
104 7 8 -1
102 105 106 107
106 1 110 2
108 16 15 -1
107 18 111 17
110 3 4 -1
105 9 109 10
111 20 19 -1
109 11 12 -1
17 865
5 668
20 3000
13 1020
11 980
8 2202
15 1897
6 1001
14 922
7 2178
19 2189
1 1267
12 3281
2 980
18 1020
10 980
3 1876
9 1197
16 980
4 576
-1 -1

输出：

12 5
20 6
8 14
19 13
7 7
15 8
3 9
1 10
9 1
13 2
18 18
6 17
2 16
10 15
11 11
16 12
14 3
17 4
5 20
4 19

比第一题简单，主要考查哈希表和树的层序遍历。

几个tips：首先是结构体部分，之前写的时候在 vector<Node> store(100); 这一句里，试图用无参构造函数去初始化 100 个 Node，但 Node 只有一个自己定义的带参构造函数，于是编译器不会合成默认构造函数，导致

error: no matching function for call to ‘Node::Node()’

改为这样就好：

struct Node
{int par = -1;int c1  = -1;int c2  = -1;int c3  = -1;Node() = default;                          // <-- 补上Node(int p, int a, int b, int c)           // 原来的: par(p), c1(a), c2(b), c3(c) {}
};

#include <iostream>
#include <vector>
#include <queue>
#include <map>
#include <algorithm>
using namespace std;struct TreeNode
{int c1 = -1;int c2 = -1;int c3 = -1;
};int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n;cin >> n;// 使用map存储树节点：编号->子节点信息map<int, TreeNode> treeMap;for (int i = 0; i < n; i++){int r, s1, s2, s3;cin >> r >> s1 >> s2 >> s3;treeMap[r] = {s1, s2, s3};}vector<pair<int, int>> flows;int gate, flowVal;while (cin >> gate >> flowVal){if (gate == -1 && flowVal == -1)break;flows.push_back({gate, flowVal});}// 按流量排序：流量降序，流量相同按编号升序sort(flows.begin(), flows.end(), [](const auto &a, const auto &b){if (a.second != b.second) return a.second > b.second;return a.first < b.first; });// 层次遍历获取登机口位置顺序vector<int> gatePositions; // 存储层次遍历得到的登机口位置queue<int> q;q.push(100); // 从根节点开始while (!q.empty()){int nodeId = q.front();q.pop();// 当前节点必须在树图中if (treeMap.find(nodeId) == treeMap.end())continue;TreeNode node = treeMap[nodeId];// 处理三个子节点：按c1->c2->c3顺序vector<int> children = {node.c1, node.c2, node.c3};for (int child : children){if (child == -1)continue;if (child < 100){ // 登机口gatePositions.push_back(child);}else{ // 分叉节点q.push(child);}}}// 输出调整结果for (int i = 0; i < flows.size(); i++){cout << flows[i].first << " " << gatePositions[i] << endl;}return 0;
}

2019：

第一题：

输入为两个数 a，b。要求输出闭区间[a,b]之间所有相邻素数组成的等差数列，三个以

上才算是序列，且对多于三个的序列，不必再输出其子序列。其中 1<=a, b<100000。求素

数的步骤必须优化。输出的每个等差数列占一行，每个数之间有空格，一行最后一个数也

有空格。输入的数据规模不会超过 int 型变量范围。

测试用例 1：

输入：

100 200

输出：

151 157 163

167 173 179

比较简单，核心在于如何高效的求解素数，这里显然是筛法！

埃拉托色尼筛法（Sieve of Eratosthenes），它是一种批量找出某个上限以内所有素数的算法，而不是单独判断一个数是否为素数。

核心思想
从 2 开始，把当前最小未被划掉的数视为素数，然后划掉它的所有倍数；重复这一过程，直到处理完 √n 为止。剩下的未被划掉的数就是素数。

第二题：

先输入 n（n < 10000），代表有 n 组数据，接下来 n 行每行输入四个数，第一个输入为

分支节点，后三个输入为其三个孩子节点（-1 代表子节点不存在）。输入的 n 行中第一行

第一个节点为根节点，作为起点。保证输入的结点至多有一个父节点。

然后输入 m（m < n），接下来输入 m 个客户，每行输入他的目标（叶节点）和优先级

（数字越小越优先，保证不会有相同优先级），要求从起点出发，按照优先级把客户送到目

标节点，然后从该节点继续运送下一个客户至其目标（叶节点），全部运送完毕后返回起

点，记录每段经过的路径，并输出。输入的数据规模不会超过 int 型变量范围。

输入：

6

100 101 102 103

101 1 104 2

102 3 105 4

103 5 6 -1

104 7 8 -1

105 9 10 -1

5

7 7

9 3

6 2

8 1

4 5

感觉坑挺多的。首先肯定要使用LCA算法（如果最近祖先是根其实就是代表要拐弯的意思），对于输出路径而言必须要求一个des它的所有祖先，这样des->lca->new_des才能拼出路径。

此外，观察输出，发现叶子结点是为起点是不打印叶子起点的。

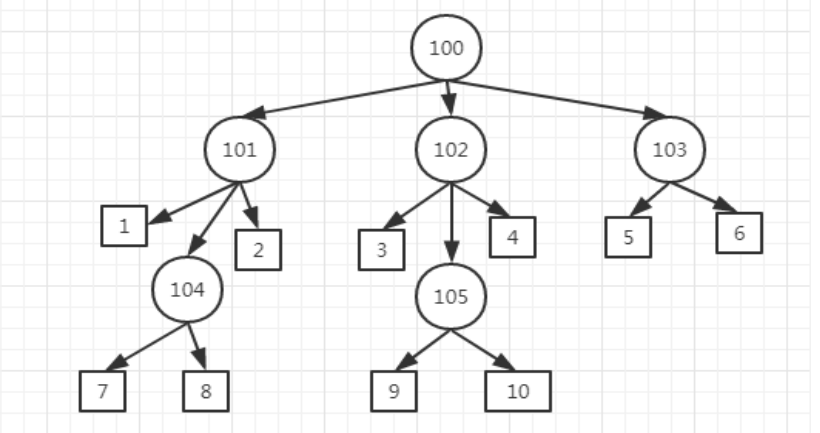
#include <bits/stdc++.h>
using namespace std;int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int n;if (!(cin >> n))return 0;unordered_map<int, array<int, 3>> children;unordered_map<int, int> parent; // child -> parentchildren.reserve(n);parent.reserve(n * 3);int r, a, b, c;int root = -1;for (int i = 0; i < n; ++i){cin >> r >> a >> b >> c;if (i == 0)root = r;children[r] = {a, b, c};if (a != -1)parent[a] = r;if (b != -1)parent[b] = r;if (c != -1)parent[c] = r;}int m;cin >> m;vector<pair<int, int>> req;req.reserve(m);for (int i = 0; i < m; ++i){int des, pri;cin >> des >> pri;req.emplace_back(des, pri);}sort(req.begin(), req.end(), [](const pair<int, int> &x, const pair<int, int> &y){ return x.second < y.second; });auto is_leaf = [&](int x) -> bool{auto it = children.find(x);if (it == children.end())return true; // 没有孩子条目 -> 叶子auto &arr = it->second;return (arr[0] == -1 && arr[1] == -1 && arr[2] == -1);};auto get_ancestors = [&](int x){vector<int> anc;int cur = x;anc.push_back(cur);while (parent.find(cur) != parent.end()){cur = parent[cur];anc.push_back(cur);}return anc; // 从 x 到 root};auto path_between = [&](int u, int v){if (u == v)return vector<int>{u};vector<int> ancU = get_ancestors(u);vector<int> ancV = get_ancestors(v);unordered_set<int> setU;setU.reserve(ancU.size() * 2);for (int x : ancU)setU.insert(x);int lca = -1;for (int x : ancV){if (setU.count(x)){lca = x;break;}}// 拼 u -> ... -> lcavector<int> path;for (int x : ancU){path.push_back(x);if (x == lca)break;}// 拼 lca -> ... -> v （不重复 lca）vector<int> down;for (int x : ancV){if (x == lca)break;down.push_back(x); // v -> ... -> child_of_lca}for (auto it = down.rbegin(); it != down.rend(); ++it)path.push_back(*it);return path;};int sta = root;for (auto &p : req){int des = p.first;vector<int> pth = path_between(sta, des); // 包含 sta 和 des// 如果起点是叶子，则按照样例要求省略起点（即不打印 sta）int start_idx = 0;if (is_leaf(sta) && !pth.empty())start_idx = 1;for (int i = start_idx; i < (int)pth.size(); ++i){cout << pth[i] << (i + 1 == (int)pth.size() ? "" : " ");if (i + 1 == (int)pth.size())cout << ""; // 保持格式if (i < (int)pth.size() - 1)cout << " ";}cout << "\n";sta = des;}// 送完后返回 root（也按样例省略起点若为叶子）vector<int> finalPath = path_between(sta, root);int start_idx = 0;if (is_leaf(sta) && !finalPath.empty())start_idx = 1;for (int i = start_idx; i < (int)finalPath.size(); ++i){cout << finalPath[i];if (i + 1 < (int)finalPath.size())cout << " ";}cout << "\n";return 0;
}

2018：

第一题：

在二维空间中给定一定数量的线段，线段的右端点的横坐标必然比左端点的横坐标大。

第一行输入 n（n < 10000），表示一共有 n 条线段。之后输入 n 行，每一行依次输入左端点

的横、纵坐标，右端点的横、纵坐标；一些线段可以连在一起，规定连接的规则只能是一条

线段的左端点和另一条线段的右端点相连，要求输出连在一起的大线段最多有多少条线段，

以及最大线段起点（左端点）的横、纵坐标。输入的数据规模不会超过 int 型变量范围。

测试用例 1：

输入：

1

1 2 2 3

输出：

1 1 2

测试用例 2：

输入：

4

1 2 2 3

2 3 3 4

3 4 4 1

2 3 5 6

输出：

3 1 2

没看懂题。

第二题：

燕子会将巢穴建立在最稳定的地方，对于三叉树而言，一个结点的子分支越多越稳定。

第一行输入 n（n < 10000），之后输入 n 行，每一行输入 4 个数字，分别为根节点，和

其左孩子、中孩子、右孩子（确保每个根已经在之前出现过）的节点编号。求前序遍历（根，

左，中，右）中子分支最多而且深度最深（高度最低）的节点编号，以及第几次遍历到该节

点。若有多个满足题目要求的结点，取最先遍历到的结点。若输入的孩子节点编号为-1，则

代表不存在此孩子分支。输入的数据规模不会超过 int 型变量范围。

count的目的是求节点是第几次遍历到的

此外，一般这些题都会和map以及struct联系在一起

此外，这题还想强调的是关于如何建自测用例:

#include <bits/stdc++.h>
using namespace std;
int n;
struct Node
{int ch1 = -1;int ch2 = -1;int ch3 = -1;Node() = default;Node(int ch1, int ch2, int ch3) : ch1(ch1), ch2(ch2), ch3(ch3) {};
};
unordered_map<int, Node> mmap;
int t, ansnode, ansdep;void dfs(int root, int depth, vector<int> &count)
{if (root == -1)return;int b = mmap[root].ch1;int c = mmap[root].ch2;int d = mmap[root].ch3;int k = 0;if (b != -1)k++;if (c != -1)k++;if (d != -1)k++;if (k > t){t = k;ansnode = root;ansdep = depth;}else if (k == t && depth > ansdep){ansnode = root;ansdep = depth;}count.push_back(root);dfs(b, depth + 1, count);dfs(c, depth + 1, count);dfs(d, depth + 1, count);return;
}int main()
{cin >> n;int a, b, c, d;int root = -1;for (int i = 0; i < n; i++){cin >> a >> b >> c >> d;mmap[a] = Node(b, c, d);if (root == -1)root = a;}using pii = pair<int, int>;t = 0;ansnode = root;ansdep = 0;vector<int> count;dfs(root, 0, count);int time = 0;for (int i = 0; i < count.size(); i++){if (count[i] == ansnode){time = i + 1;break;}}cout << ansnode << " " << time << endl;return 0;
}

2017:

第一题：

先输入一个整型数字 N（1 <= N < 1000000），接着输入 N 个无序的数字。要求输出非递

减顺序排列后的中位数，以及该中位数输入的次序。如果 N 为偶数，则分两行输出有两个

中位数，如果 N 为奇数，输出最中间的数即可。输入的数据可能重复，当输入数据相同时，

优先输入的排在前面。所有输入的数据不会超过 int 型变量的范围。

测试用例 1：

输入：

5

9 2 7 1 6

输出：

6 5

对于实现稳定排序，c++里面的sort只需要把比较符定义好就行：

struct node {int x, t; //输入的数值和次序
}num[maxn];
bool cmp(node a, node b) {if(a.x == b.x) return a.t < b.t;return a.x < b.x;
}

还有一个做法是直接套用稳定排序std：

stable_sort(store.begin(), store.end(), [](const Node& A, const Node& B) {return A.num < B.num; // stable_sort 保证相等时前者先于后者});

对于归并排序，c++中的稳定排序，实现：

在实现上，正确、鲁棒的做法是对每个 left 明确算出 mid = min(left+s-1,n-1) 和 right = min(left+2*s-1,n-1)，并且只在 left + s < n 时合并（条件明晰，这样就省去了复杂且易出错的判断）

注意：合并的时候下标要对齐：store[i] = temp[i - le];

#include <bits/stdc++.h>
using namespace std;
int n;
struct Node
{int num;int pos;Node() = default;Node(int num, int pos) : num(num), pos(pos) {}
};
vector<Node> store;// 把 [le..mid] 和 [mid+1..ri] 合并到有序
void merge_segment(int le, int mid, int ri)
{vector<Node> temp;int a = le;int b = mid + 1;while (a <= mid && b <= ri){if (store[a].num <= store[b].num){temp.push_back(store[a++]);}else{temp.push_back(store[b++]);}}while (a <= mid)temp.push_back(store[a++]);while (b <= ri)temp.push_back(store[b++]);for (int i = le; i <= ri; ++i)store[i] = temp[i - le];
}void iterative_merge_sort()
{if (n <= 1)return;for (int s = 1; s < n; s <<= 1){// 每次处理长度为 s 的一对对区间for (int left = 0; left < n - s; left += 2 * s){int mid = left + s - 1;int right = min(left + 2 * s - 1, n - 1);merge_segment(left, mid, right);}}
}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cin >> n;store.reserve(n);for (int i = 1; i <= n; ++i){int a;cin >> a;store.emplace_back(a, i);}iterative_merge_sort();if (n % 2 == 1){cout << store[n / 2].num << " " << store[n / 2].pos << "\n";}else{cout << store[n / 2 - 1].num << " " << store[n / 2 - 1].pos << "\n";cout << store[n / 2].num << " " << store[n / 2].pos << "\n";}return 0;
}

再次强调主归并的标准写法：

for (int s = 1; s < n; s <<= 1){// 每次处理长度为 s 的一对对区间for (int left = 0; left < n - s; left += 2 * s){int mid = left + s - 1;int right = min(left + 2 * s - 1, n - 1);merge_segment(left, mid, right);}}

第二题：

输入若干行（总行数不超过），每一行的第一个输入为家谱中的某成员，该行接着输入

的信息为该成员两个孩子的姓名（保证除第一行的第一个成员外，每行第一个成员都在之前

输入过）。

输入完毕后，最后一行输入两个成员（保证已输入过），为要求查找的两个家谱成员的

关系，输出内容包括他们最近邻的共同祖先的名字以及在家谱中相差的层次数。

测试用例 1：

输入：

Ye Shu Ba

Shu Ge Mei1

Ba Self Mei2

Ge Son1 Son2

Son2 Mei1

输出：

Shu 1

考查非常经典的树结构，与LCA算法！

（这里可以完善一下，在使用之前先判断a有没有children）

#include <bits/stdc++.h>
using namespace std;int findlca(int a, int u, int v, const vector<pair<int, int>> &childs)
{if (a == -1)return -1;if (a == u || a == v)return a;int left = childs[a].first;int right = childs[a].second;int k1 = -1, k2 = -1;if (left != -1)k1 = findlca(left, u, v, childs);if (right != -1)k2 = findlca(right, u, v, childs);if (k1 != -1 && k2 != -1)return a;return (k1 != -1) ? k1 : k2;
}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int n;if (!(cin >> n))return 0;unordered_map<string, int> mmap;vector<string> id2name;vector<int> parents;           // parents[i] = parent id or -1vector<pair<int, int>> childs; // childs[i] = {left, right}, -1 表示无子int cnt = 0;auto ensure = [&](const string &s) -> int{auto it = mmap.find(s);if (it != mmap.end())return it->second;int id = cnt++;mmap[s] = id;id2name.push_back(s);parents.push_back(-1);childs.push_back({-1, -1});return id;};for (int i = 0; i < n; ++i){string a, b, c;cin >> a >> b >> c;int pa = ensure(a);int pb = ensure(b);int pc = ensure(c);parents[pb] = pa;parents[pc] = pa;childs[pa] = {pb, pc};}string s1, s2;cin >> s1 >> s2;if (!mmap.count(s1) || !mmap.count(s2))return 0;int u = mmap[s1];int v = mmap[s2];// 找 rootint root = -1;for (int i = 0; i < cnt; ++i)if (parents[i] == -1){root = i;break;}if (root == -1)return 0;int lca = findlca(root, u, v, childs);if (lca == -1){// 理论上不该发生（输入保证在同一棵树），但防御性输出cout << "-1 0\n";return 0;}auto dist = [&](int node, int anc){int steps = 0;while (node != anc){node = parents[node];steps++;if (node == -1)break; // 防御性}return steps;};int du = dist(u, lca);int dv = dist(v, lca);cout << id2name[lca] << " " << abs(du - dv) << "\n";return 0;
}#include <bits/stdc++.h>
using namespace std;int findlca(int a, int u, int v, const vector<pair<int, int>> &childs)
{if (a == -1)return -1;if (a == u || a == v)return a;int left = childs[a].first;int right = childs[a].second;int k1 = -1, k2 = -1;if (left != -1)k1 = findlca(left, u, v, childs);if (right != -1)k2 = findlca(right, u, v, childs);if (k1 != -1 && k2 != -1)return a;return (k1 != -1) ? k1 : k2;
}

此外，上面的是给了输入数量N的写法，如果没有给n？

使用getline(cin, line）读一整行的输入！然后利用空格划分字符串。

2016：

第一题：

给定一个数 n（0 < n < 1000000），将这个数的各位顺序颠倒，成为逆序数 m。例如 1234

的逆序数为 4321。如果 m 是 n 的 k 倍（k 是整数），那么输出 n*k=m。例如输入 1089，输

出 1089*9=9801。如果 m 不是 n 的整数倍，那么输出 n 和 n 的逆序数，例如输入 1234，输

出 1234 4321。再例输入 23200，输出 23200 00232。已知输入开头不包含多余的 0。

用c++很简单。注意使用函数！to_string与stoi

#include <bits/stdc++.h>
using namespace std;
int n;int main()
{cin >> n;string ori = to_string(n);string change = ori;reverse(change.begin(), change.end());int m = stoi(change);// cout << change << endl;// cout << m << endl;if (m > 0 && m % n == 0){cout << n << '*' << m / n << '=' << m << endl;}elsecout << ori << " " << change << endl;return 0;
}

第二题：

enum 是枚举（enumerate）的缩写，在 C 语言中是一种基本数据类型，它可以让数据更

简洁，更易读。规定各项的值只能是 int 型变量，若未定义第一项的值，则默认第一项的值

从 0 开始；若已定义某项的值，则从该项后值递增加一。

输入一行 c 语言的 enum 定义语句，且符合 C 语言语法。各项在大括号之间，并保证大

括号之间无空格。要求输出各项的名称和对应的值，占一行，且名称与值之间有一个空格。

保证输入的长度不超过 1000000 个字符，且项至多为 1000 个，每个项的长度至多为 1000 个

字符。

测试用例 1：

输入：

enum BOOL{true,false};

输出：

true 0

false 1

同样，由于输入是存在空格的，所以用getline读入一行。找{作为起始点，然后根据逗号划分字符串。

#include <bits/stdc++.h>
using namespace std;
string s;
int main()
{getline(cin, s);int len = s.size();int pos = -1;for (int i = 0; i < len; i++){if (s[i] != '{')continue;else{pos = i;break;}}int k = pos + 1;vector<string> ori;string t = "";while (k < len - 2){if (s[k] != ','){t += s[k];k++;}else{ori.push_back(t);t.clear();k++;}}ori.push_back(t);using psi = pair<string, int>;vector<psi> ans;for (string str : ori){int len = str.size();int n_pos = -1;for (int i = 0; i < len; i++){if (str[i] == '='){n_pos = i;break;}}if (n_pos == -1)ans.push_back(make_pair(str, n_pos));else{int z = stoi(str.substr(n_pos + 1));ans.push_back(make_pair(str.substr(0, n_pos), z));}}int pre = 0;for (auto ele : ans){auto [name, num] = ele;if (num == -1)ele.second = pre++;else if (num != -1)pre = num + 1;cout << ele.first << " " << ele.second << endl;}return 0;
}

2015：

第一题：

相亲数，又称亲和数、友爱数、友好数，指两个正整数中，彼此的全部约数之和（本身

除外）与另一方相等。毕达哥拉斯曾说：“朋友是你灵魂的倩影，要像 220 与 284 一样亲密。”

输入两个正整数 a 和 b（1< a, b <1000000）。若 a 的所有约数（包括 1，但不包括 a 本

身）的和等于 b，且 b 的所有约数（包括 1，但不包括 b 的本身）的和等于 a，则两个数是

相亲数。

输入保证 a，b 不相等，且 a，b 的因子数目均不超过 1000 个。要求用两行分别输出两

个正整数 a，b 和其约数求和的式子，并求出其约数和。再换行输出 1 或者 0，表示这两个

数是否为一对相亲数。要求 a，b 与和式之间有逗号和空格，且和式中的约数顺序是从小到

大的。

测试用例 1：

输入：

220 284

输出：

220, 1+2+4+5+10+11+20+22+44+55+110=284

284, 1+2+4+71+142=220

1

测试用例 2：

输入：

1952 2015

输出：

1952, 1+2+4+8+16+32+61+122+244+488+976=1954

2015, 1+5+13+31+65+155+403=673

0

最后需要注意一点的是，边扫描边求和边打印，一次循环干三件事应该是最优的代码

数据量不大，先试试暴力，直接遍历到n/2求因子。

#include <bits/stdc++.h>
using namespace std;
int a, b;void count(int x, vector<int> &store)
{for (int i = 1; i <= x / 2 + 1; i++){if (x % i == 0)store.push_back(i);}return;
}int main()
{cin >> a >> b;vector<int> numa;vector<int> numb;count(a, numa);count(b, numb);string outa = "";int len = numa.size();for (int i = 0; i < len - 1; i++){outa = outa + to_string(numa[i]) + '+';}outa = outa + to_string(numa[len - 1]) + '=';int tota = accumulate(numa.begin(), numa.end(), 0);outa += to_string(tota);string outb = "";len = numb.size();for (int i = 0; i < len - 1; i++){outb = outb + to_string(numb[i]) + '+';}outb = outb + to_string(numb[len - 1]) + '=';int totb = accumulate(numb.begin(), numb.end(), 0);outb += to_string(totb);cout << a << ", " << outa << endl;cout << b << ", " << outb << endl;cout << int(tota == b && totb == a) << endl;return 0;
}

第二题：

先输入一个整数 n（2 <= n <= 10000），表示桌面窗口的数量，再输入 n 行，每行 5 个

数，分别为窗口 ID，窗口右下角横坐标，右下角纵坐标，左上角横坐标，左上角纵坐标（坐

标均以屏幕左下角为原点，并假设屏幕无限大，窗口均为矩形窗口），先输入的窗口叠放在

后输入的窗口的上面。

再输入 m 行，表示 m 次点击，每行两个数，分别表示点击的横坐标和纵坐标。

所有的输入内容保证都是整数，且均在 int 型表示的范围内。若窗口有重合，则认为点

击到更靠上的窗口；若点击到窗口的边框上，也算点击到该窗口。一旦点击到某一窗口，则

该窗口将会变为最上面的窗口。要求在 m 次点击后，按窗口叠放次序从上到下依次输出窗

口的 ID。每个 ID 的后面都有一个空格，并在末尾换行。

测试用例 1：

输入：

2

1 5 1 1 5

2 7 1 3 5

3

1 2

4 3

6 4

输出：

2 1

之前写代码，代码的致命错误是用 new Node() 创建临时 pre，导致删除首节点时形成自环（p->next = head 把自己指向自己）。——所以引入哨兵节点做统一真的很重要！

思路倒简单，写成链表，初始尾插这些窗口，然后遍历点击，如果点到了，删除该节点，把节点挪到开头。

#include <bits/stdc++.h>
using namespace std;
using t4i = tuple<int, int, int, int>;
struct Node
{int id = -1;t4i pos = {0, 0, 0, 0};Node *next = nullptr;Node() = default;
};
int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n;int id, a, b, c, d;Node *head = nullptr;Node *tail = nullptr;for (int i = 0; i < n; ++i){cin >> id >> a >> b >> c >> d;Node *p = new Node();p->id = id;p->pos = {a, b, c, d};if (!head){head = tail = p;}else{tail->next = p;tail = p;}}cin >> m;int x, y;for (int i = 0; i < m; ++i){cin >> x >> y;Node dummy; // 使用栈上的哨兵dummy.next = head;Node *pre = &dummy;Node *p = head;while (p != nullptr){auto [rix, riy, lex, ley] = p->pos;if (lex <= x && x <= rix && riy <= y && y <= ley){pre->next = p->next;head = dummy.next;p->next = head;head = p;break;}else{pre = p;p = p->next;}}}Node *cur = head;while (cur){cout << cur->id << " ";cur = cur->next;}cout << "\n";return 0;
}

第三题：

输入一段含标点的英文语段（若干行，以文件终止符 EOF 结束，在命令窗口中以 ctrl+z

表示），保证每行输入的单词都是完整的，词与词之间至少会出现空格或标点，且词不会被

换行所分割。

保证输入的所有字母都是小写，且每行输入的长度不会超过 100000，输入单词总数不

会超过 1000 个，每个单词的长度不超过 100。

统计这段话中出现的所有单词，要求按字典顺序输出词语，且不能重复，每输出一个词

换一行。

测试用例 1：

输入：

we are family.

you and me are family, you are my sister.

输出：

and

are

family

me

my

sister

we

you

说明一个点：

std::getline 在 读到换行符 和 读到 EOF 时的行为：

• std::getline(istream& is, string& str) 会一直从流 is 中读字符，直到遇到换行符 或 EOF 为止。

• 当遇到换行符：

  • 换行符本身 不会存入 str。

  • getline 会丢弃这个换行符（把它从输入流里读走，但不放到结果字符串里）。

  • 函数返回后，str 中存的就是该行的内容（不包含行尾的 \n）。

• 返回值：成功读取到一行 → getline 返回一个非空的 istream&，在布尔上下文中为 true。

还有就是在结尾要判断一下有没有多余的还没放进去

#include <bits/stdc++.h>
using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);set<string> mset;string s;while (getline(cin, s)) {string t;for (char ch : s) {// 题目保证都是小写字母，但用 islower 更通用一点if (ch >= 'a' && ch <= 'z') {t.push_back(ch);} else {if (!t.empty()) {mset.insert(t);t.clear();}}}// 行结尾后，若有缓存的单词也要插入if (!t.empty()) {mset.insert(t);}}for (const auto &w : mset) {cout << w << '\n';}return 0;
}