启发式搜索--模拟退火算法 matlab
一、背景
贪心算法失效:陷入局部最优
二、思想
该点位置高,直接去;位置低,利用距离决定是否去
三、关键点
1.设置temperature,使跳动结束
2.设置概率函数,使到最优解的概率最大
四、适用赛题:可行解过多、NP-hard问题
Q1.求给定函数最值问题
1.一元函数
产生新解:找附近的一个x值,生成对应的fx,进行比较
%% SA 模拟退火: 求解函数y = 11*sin(x) + 7*cos(5*x)在[-3,3]内的最大值(动画演示)
tic
clear; clc%% 绘制函数的图形
x = -3:0.1:3;
y = 11*sin(x) + 7*cos(5*x);
figure
plot(x,y,'b-')
hold on % 不关闭图形,继续在上面画图%% 参数初始化
narvs = 1; % 变量个数
T0 = 100; % 初始温度
T = T0; % 迭代中温度会发生改变,第一次迭代时温度就是T0
maxgen = 200; % 最大迭代次数
Lk = 100; % 每个温度下的迭代次数
alfa = 0.95; % 温度衰减系数
x_lb = -3; % x的下界
x_ub = 3; % x的上界%% 随机生成一个初始解
x0 = zeros(1,narvs);
for i = 1: narvsx0(i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(1);
end
y0 = Obj_fun1(x0); % 计算当前解的函数值
h = scatter(x0,y0,'*r'); % scatter是绘制二维散点图的函数(这里返回h是为了得到图形的句柄,未来我们对其位置进行更新)%% 定义一些保存中间过程的量,方便输出结果和画图
max_y = y0; % 初始化找到的最佳的解对应的函数值为y0
MAXY = zeros(maxgen,1); % 记录每一次外层循环结束后找到的max_y (方便画图)%% 模拟退火过程
for iter = 1 : maxgen % 外循环, 我这里采用的是指定最大迭代次数for i = 1 : Lk % 内循环,在每个温度下开始迭代y = randn(1,narvs); % 生成1行narvs列的N(0,1)随机数z = y / sqrt(sum(y.^2)); % 根据新解的产生规则计算zx_new = x0 + z*T; % 根据新解的产生规则计算x_new的值% 如果这个新解的位置超出了定义域,就对其进行调整for j = 1: narvsif x_new(j) < x_lb(j)r = rand(1);x_new(j) = r*x_lb(j)+(1-r)*x0(j);elseif x_new(j) > x_ub(j)r = rand(1);x_new(j) = r*x_ub(j)+(1-r)*x0(j);endendx1 = x_new; % 将调整后的x_new赋值给新解x1y1 = Obj_fun1(x1); % 计算新解的函数值if y1 > y0 % 如果新解函数值大于当前解的函数值x0 = x1; % 更新当前解为新解y0 = y1;elsep = exp(-(y0 - y1)/T); % 根据Metropolis准则计算一个概率if rand(1) < p % 生成一个随机数和这个概率比较,如果该随机数小于这个概率x0 = x1; % 更新当前解为新解y0 = y1;endend% 判断是否要更新找到的最佳的解if y0 > max_y % 如果当前解更好,则对其进行更新max_y = y0; % 更新最大的ybest_x = x0; % 更新找到的最好的xendendMAXY(iter) = max_y; % 保存本轮外循环结束后找到的最大的yT = alfa*T; % 温度下降pause(0.01) % 暂停一段时间(单位:秒)后再接着画图h.XData = x0; % 更新散点图句柄的x轴的数据(此时解的位置在图上发生了变化)h.YData = Obj_fun1(x0); % 更新散点图句柄的y轴的数据(此时解的位置在图上发生了变化)
enddisp('最佳的位置是:'); disp(best_x)
disp('此时最优值是:'); disp(max_y)pause(0.5)
h.XData = []; h.YData = []; % 将原来的散点删除
scatter(best_x,max_y,'*r'); % 在最大值处重新标上散点
title(['模拟退火找到的最大值为', num2str(max_y)]) % 加上图的标题%% 画出每次迭代后找到的最大y的图形
figure
plot(1:maxgen,MAXY,'b-');
xlabel('迭代次数');
ylabel('y的值');
toc
2.二元函数
%% SA 模拟退火: 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值(动画演示)
ticclear; clc
%% 绘制函数的图形
figure
x1 = -15:1:15;
x2 = -15:1:15;
[x1,x2] = meshgrid(x1,x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2,y)
xlabel('x1'); ylabel('x2'); zlabel('y'); % 加上坐标轴的标签
axis vis3d % 冻结屏幕高宽比,使得一个三维对象的旋转不会改变坐标轴的刻度显示
hold on % 不关闭图形,继续在上面画图%% 参数初始化
narvs = 2; % 变量个数
T0 = 100; % 初始温度
T = T0; % 迭代中温度会发生改变,第一次迭代时温度就是T0
maxgen = 200; % 最大迭代次数
Lk = 100; % 每个温度下的迭代次数
alfa = 0.95; % 温度衰减系数
x_lb = [-15 -15]; % x的下界
x_ub = [15 15]; % x的上界%% 随机生成一个初始解
x0 = zeros(1,narvs);
for i = 1: narvsx0(i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(1);
end
y0 = Obj_fun2(x0); % 计算当前解的函数值
h = scatter3(x0(1),x0(2),y0,'*r'); % scatter3是绘制三维散点图的函数(这里返回h是为了得到图形的句柄,未来我们对其位置进行更新)%% 定义一些保存中间过程的量,方便输出结果和画图
min_y = y0; % 初始化找到的最佳的解对应的函数值为y0
MINY = zeros(maxgen,1); % 记录每一次外层循环结束后找到的min_y (方便画图)%% 模拟退火过程
for iter = 1 : maxgen % 外循环, 我这里采用的是指定最大迭代次数for i = 1 : Lk % 内循环,在每个温度下开始迭代y = randn(1,narvs); % 生成1行narvs列的N(0,1)随机数z = y / sqrt(sum(y.^2)); % 根据新解的产生规则计算zx_new = x0 + z*T; % 根据新解的产生规则计算x_new的值% 如果这个新解的位置超出了定义域,就对其进行调整for j = 1: narvsif x_new(j) < x_lb(j)r = rand(1);x_new(j) = r*x_lb(j)+(1-r)*x0(j);elseif x_new(j) > x_ub(j)r = rand(1);x_new(j) = r*x_ub(j)+(1-r)*x0(j);endendx1 = x_new; % 将调整后的x_new赋值给新解x1y1 = Obj_fun2(x1); % 计算新解的函数值if y1 < y0 % 如果新解函数值小于当前解的函数值x0 = x1; % 更新当前解为新解y0 = y1;elsep = exp(-(y1 - y0)/T); % 根据Metropolis准则计算一个概率if rand(1) < p % 生成一个随机数和这个概率比较,如果该随机数小于这个概率x0 = x1; % 更新当前解为新解y0 = y1;endend% 判断是否要更新找到的最佳的解if y0 < min_y % 如果当前解更好,则对其进行更新min_y = y0; % 更新最小的ybest_x = x0; % 更新找到的最好的xendendMINY(iter) = min_y; % 保存本轮外循环结束后找到的最小的yT = alfa*T; % 温度下降pause(0.02) % 暂停一段时间后(单位:秒)再接着画图h.XData = x0(1); % 更新散点图句柄的x轴的数据(此时解的位置在图上发生了变化)h.YData = x0(2); % 更新散点图句柄的y轴的数据(此时解的位置在图上发生了变化)h.ZData = Obj_fun2(x0); % 更新散点图句柄的z轴的数据(此时粒子的位置在图上发生了变化)
enddisp('最佳的位置是:'); disp(best_x)
disp('此时最优值是:'); disp(min_y)pause(0.5)
h.XData = []; h.YData = []; h.ZData = []; % 将原来的散点删除
scatter3(best_x(1), best_x(2), min_y,'*r'); % 在最小值处重新标上散点
title(['模拟退火找到的最小值为', num2str(min_y)]) % 加上图的标题%% 画出每次迭代后找到的最小y的图形
figure
plot(1:maxgen,MINY,'b-');
xlabel('迭代次数');
ylabel('y的值');
toc
Q2:旅行商问题(Traveling Saleman Problem,TSP)
给定一系列城市和没对城市之间的距离,访问每一座城市再回到初始城市的最短回路
三种产生新解的方法:交换法、移位法、倒置法
%% 模拟退火解决TSP问题tic
rng('shuffle') % 控制随机数的生成,否则每次打开matlab得到的结果都一样
% https://ww2.mathworks.cn/help/matlab/math/why-do-random-numbers-repeat-after-startup.html
% https://ww2.mathworks.cn/help/matlab/ref/rng.html
clear;clc
% 38个城市,TSP数据集网站(http://www.tsp.gatech.edu/world/djtour.html) 上公测的最优结果6656。
coord = [11003.611100,42102.500000;11108.611100,42373.888900;11133.333300,42885.833300;11155.833300,42712.500000;11183.333300,42933.333300;11297.500000,42853.333300;11310.277800,42929.444400;11416.666700,42983.333300;11423.888900,43000.277800;11438.333300,42057.222200;11461.111100,43252.777800;11485.555600,43187.222200;11503.055600,42855.277800;11511.388900,42106.388900;11522.222200,42841.944400;11569.444400,43136.666700;11583.333300,43150.000000;11595.000000,43148.055600;11600.000000,43150.000000;11690.555600,42686.666700;11715.833300,41836.111100;11751.111100,42814.444400;11770.277800,42651.944400;11785.277800,42884.444400;11822.777800,42673.611100;11846.944400,42660.555600;11963.055600,43290.555600;11973.055600,43026.111100;12058.333300,42195.555600;12149.444400,42477.500000;12286.944400,43355.555600;12300.000000,42433.333300;12355.833300,43156.388900;12363.333300,43189.166700;12372.777800,42711.388900;12386.666700,43334.722200;12421.666700,42895.555600;12645.000000,42973.333300];
n = size(coord,1); % 城市的数目figure % 新建一个图形窗口
plot(coord(:,1),coord(:,2),'o'); % 画出城市的分布散点图
hold on % 等一下要接着在这个图形上画图的d = zeros(n); % 初始化两个城市的距离矩阵全为0
for i = 2:n for j = 1:i coord_i = coord(i,:); x_i = coord_i(1); y_i = coord_i(2); % 城市i的横坐标为x_i,纵坐标为y_icoord_j = coord(j,:); x_j = coord_j(1); y_j = coord_j(2); % 城市j的横坐标为x_j,纵坐标为y_jd(i,j) = sqrt((x_i-x_j)^2 + (y_i-y_j)^2); % 计算城市i和j的距离end
end
d = d+d'; % 生成距离矩阵的对称的一面%% 参数初始化
T0 = 1000; % 初始温度
T = T0; % 迭代中温度会发生改变,第一次迭代时温度就是T0
maxgen = 1000; % 最大迭代次数
Lk = 500; % 每个温度下的迭代次数
alpfa = 0.95; % 温度衰减系数%% 随机生成一个初始解
path0 = randperm(n); % 生成一个1-n的随机打乱的序列作为初始的路径
result0 = calculate_tsp_d(path0,d); % 调用我们自己写的calculate_tsp_d函数计算当前路径的距离%% 定义一些保存中间过程的量,方便输出结果和画图
min_result = result0; % 初始化找到的最佳的解对应的距离为result0
RESULT = zeros(maxgen,1); % 记录每一次外层循环结束后找到的min_result (方便画图)%% 模拟退火过程
for iter = 1 : maxgen % 外循环, 我这里采用的是指定最大迭代次数for i = 1 : Lk % 内循环,在每个温度下开始迭代path1 = gen_new_path(path0); % 调用我们自己写的gen_new_path函数生成新的路径result1 = calculate_tsp_d(path1,d); % 计算新路径的距离%如果新解距离短,则直接把新解的值赋值给原来的解if result1 < result0 path0 = path1; % 更新当前路径为新路径result0 = result1; elsep = exp(-(result1 - result0)/T); % 根据Metropolis准则计算一个概率if rand(1) < p % 生成一个随机数和这个概率比较,如果该随机数小于这个概率path0 = path1; % 更新当前路径为新路径result0 = result1; endend% 判断是否要更新找到的最佳的解if result0 < min_result % 如果当前解更好,则对其进行更新min_result = result0; % 更新最小的距离best_path = path0; % 更新找到的最短路径endendRESULT(iter) = min_result; % 保存本轮外循环结束后找到的最小距离T = alpfa*T; % 温度下降
enddisp('最佳的方案是:'); disp(mat2str(best_path))
disp('此时最优值是:'); disp(min_result)best_path = [best_path,best_path(1)]; % 在最短路径的最后面加上一个元素,即第一个点(我们要生成一个封闭的图形)
n = n+1; % 城市的个数加一个(紧随着上一步)
for i = 1:n-1 j = i+1;coord_i = coord(best_path(i),:); x_i = coord_i(1); y_i = coord_i(2); coord_j = coord(best_path(j),:); x_j = coord_j(1); y_j = coord_j(2);plot([x_i,x_j],[y_i,y_j],'-b') % 每两个点就作出一条线段,直到所有的城市都走完
% pause(0.02) % 暂停0.02s再画下一条线段hold on
end%% 画出每次迭代后找到的最短路径的图形
figure
plot(1:maxgen,RESULT,'b-');
xlabel('迭代次数');
ylabel('最短路径');toc
% calculate_tsp_d.mfunction result = calculate_tsp_d(path,d)
% 输入:path:路径(1至n的一个序列),d:距离矩阵n = length(path);result = 0; % 初始化该路径走的距离为0for i = 1:n-1 result = d(path(i),path(i+1)) + result; % 按照这个序列不断的更新走过的路程这个值end result = d(path(1),path(n)) + result; % 别忘了加上从最后一个城市返回到最开始那个城市的距离
end
Q3:书店买书问题(0-1规划)
15书店,20本书,书店运费在最后一列,怎样选择买书方案
data:
产生新解的方法:随机选择一家书店进行更换
%% 模拟退火解决书店买书问题 % 466
tic
rng('shuffle') % 控制随机数的生成,否则每次打开matlab得到的结果都一样load book_data % 这个文件一定要在当前文件夹下面
% 这个数据文件里面保存了两个矩阵:M是每本书在每家店的价格; freight表示每家店的运费
[s, b] = size(M); % s是书店的数量,b是要购买的书的数量%% 参数初始化
T0 = 1000; % 初始温度
T = T0; % 迭代中温度会发生改变,第一次迭代时温度就是T0
maxgen = 500; % 最大迭代次数
Lk = 200; % 每个温度下的迭代次数
alfa = 0.95; % 温度衰减系数%% 随机生成一个初始解
way0 = randi([1, s],1,b); % 在1-s这些整数中随机抽取一个1*b的向量,表示这b本书分别在哪家书店购买
money0 = calculate_money(way0,freight,M,b); % 调用我们自己写的calculate_money函数计算这个方案的花费%% 定义一些保存中间过程的量,方便输出结果和画图
min_money = money0; % 初始化找到的最佳的解对应的花费为money0
MONEY = zeros(maxgen,1); % 记录每一次外层循环结束后找到的min_money (方便画图)%% 模拟退火过程
for iter = 1 : maxgen % 外循环, 我这里采用的是指定最大迭代次数for i = 1 : Lk % 内循环,在每个温度下开始迭代way1 = gen_new_way(way0,s,b); % 调用我们自己写的gen_new_way函数生成新的方案money1 = calculate_money(way1,freight,M,b); % 计算新方案的花费if money1 < money0 % 如果新方案的花费小于当前方案的花费way0 = way1; % 更新当前方案为新方案money0 = money1;elsep = exp(-(money1 - money0)/T); % 根据Metropolis准则计算一个概率if rand(1) < p % 生成一个随机数和这个概率比较,如果该随机数小于这个概率way0 = way1;money0 = money1;endend% 判断是否要更新找到的最佳的解if money0 < min_money % 如果当前解更好,则对其进行更新min_money = money0; % 更新最小的花费best_way = way0; % 更新找到的最佳方案endendMONEY(iter) = min_money; % 保存本轮外循环结束后找到的最小花费T = alfa*T; % 温度下降
enddisp('最佳的方案是:'); disp(mat2str(best_way))
disp('此时最优值是:'); disp(min_money)%% 画出每次迭代后找到的最佳方案的图形
figure
plot(1:maxgen,MONEY,'b-');
xlabel('迭代次数');
ylabel('最小花费');
toc
% calculate_money.mfunction money = calculate_money(way,freight,M,b)
% 输入:way: 购买方案; fright:运费; M: 每本书在每家店的价格; b:一共要购买几本书index = unique(way); % 在哪些商店购买了商品,因为我们等下要计算运费money = sum(freight(index)); % 计算买书花费的运费% 计算总花费:刚刚计算出来的运费 + 五本书的售价for i = 1:b money = money + M(way(i),i); end
end
Q4:背包问题(整数规划)
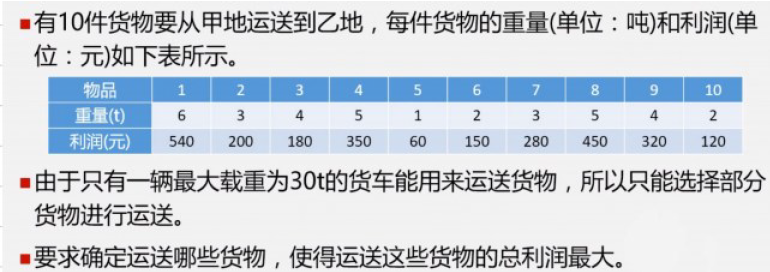
%% 模拟退火求解背包问题,本题的最优解是2410
% 因为这题只有十个物品,用枚举法其实也能做出来
% 建模中遇到了背包问题还是用intlinprog函数哦~这题只是训练大家的编程和建模的思维profit = [540 200 180 350 60 150 280 450 320 120]; % 每件物品的利润
weight = [6 3 4 5 1 2 3 5 4 2]; % 每件物品的重量
max_weight = 30; % 最大装载重量
n = length(profit); % 物品个数%% 参数初始化
T0 = 1000; % 初始温度
T = T0; % 迭代中温度会发生改变,第一次迭代时温度就是T0
maxgen = 500; % 最大迭代次数
Lk = 200; % 每个温度下的迭代次数
alfa = 0.95; % 温度衰减系数%% 生成初始解
way0 = zeros(1,n); % 初始解中每个元素都为0,表示一件物品都不装
profit0 = sum(way0 .* profit); % 计算这个装载方案的利润%% 定义一些保存中间过程的量,方便输出结果和画图
max_profit = profit0; % 初始化找到的最佳的解对应的利润为profit0
PROFIT = zeros(maxgen,1); % 记录每一次外层循环结束后找到的max_profit (方便画图)%% 模拟退火过程
for iter = 1 : maxgen % 外循环, 我这里采用的是指定最大迭代次数for i = 1 : Lk % 内循环,在每个温度下开始迭代 weight0 = sum(way0 .* weight); % 计算这个装载方案的重量[way1, delta_weight] = gen_new_way(way0, n, weight); % 调用我们自己写的gen_new_way函数生成新的装载方案profit1 = sum(way1 .* profit); % 计算新装载方案的利润if weight0 + delta_weight > max_weight % 如果超重了,就不操作[]; % 空语句,相当于啥都不干elseif profit1 > profit0 % 如果没有超重,而且新装载方案的利润更高way0 = way1; % 更新当前装载方案为新装载方案profit0 = profit1;elsep = exp(-(profit0 - profit1)/T); % 根据Metropolis准则计算一个概率if rand(1) < p % 生成一个随机数和这个概率比较,如果该随机数小于这个概率way0 = way1; % 更新当前装载方案为新装载方案profit0 = profit1;endend% 判断是否要更新找到的最佳的解if profit0 > max_profit % 如果当前解更好,则对其进行更新max_profit = profit0; % 更新最大的利润best_way = way0; % 更新找到的最好的装载方案endendPROFIT(iter) = max_profit; % 保存本轮外循环结束后找到的最大的利润T = alfa*T; % 温度下降
enddisp('最佳的方案是:'); disp(best_way)
disp('此时最优值是:'); disp(max_profit)
function [way1, delta_weight] = gen_new_way(way0, n, weight)
% way0:原来的装载方案; n是物品个数 ; weight是物品的重量
% way1:新的装载方案; delta_weight:重量的变化量i = randi([1,n],1); % 随机选取一个物品iif way0(i) == 1 % 如果物品i在原来的背包中way0(i) = 0; % 从背包里取出物品iempty_ind = find(way0==0); % 看看背包中哪几个位置是空的length_empth_ind = length(empty_ind); % 计算空位置的个数ind = randi([1, length_empth_ind], 1); % 在这几个空位置中取一个随机下标 j = empty_ind(ind); % j就是随机选择出来的背包中的某个空位置way0(j) = 1; % 装入物品jdelta_weight = weight(j) - weight(i); % 计算重量的变化量else % 如果物品i原来就不在背包中way0(i) = 1; % 在背包中放入物品idelta_weight = weight(i); % 计算重量的变化量if rand(1) < 0.5 % 判断是否需要再取出一个物品(这里的0.5是需要再取出物品的概率,可以自己调整)fill_ind = find(way0==1); % 看看背包中哪几个位置有物品length_fill_ind = length(fill_ind); % 计算有物品的位置的个数ind = randi([1, length_fill_ind], 1); % 在这几个有物品的位置中取一个随机下标 j = fill_ind(ind); % j就是随机选择出来的背包中的某个有物品的位置way0(j) = 0; % 取出物品jdelta_weight = weight(i) - weight(j); % 计算重量的变化量endendway1 = way0; % 将调整后的way0赋值给way1
endeg:寝室同学兴趣爱好问题
题目:40名同学 需要分到 10个寝室,我们通过调查问卷得到了这 40 名同 学的兴趣爱好,请问怎么划分 寝室 能够保证 :不同寝室间, 同寝室 同学的 共爱好数量分布尽 可能 均匀 。
思路:先计算出同学们两两爱好数量关系,之后利用模拟退火进行方差最小的优化
数据预处理
import numpy as np
import pandas as pd
df = pd.read_csv(r'data.csv')
data = df.iloc[:,1].tolist()
data = [set(i.replace('其他','').strip('、').split('、')) for i in data]、
# 去掉 ‘其他’ 和‘、’ 然后对爱好进行进行切割 ,之后转化为集合
result = [len(i & j) for i in data for j in data] # 求交集个数
result = np.array(result).reshape(len(data),-1) # 转化为40*40的矩阵
np.savetxt(r'mydata.csv', result, delimiter=',') 模拟退火
% main.mclear;clc
tic
rng('shuffle') % 控制随机数的生成,否则每次打开matlab得到的结果都一样
% https://ww2.mathworks.cn/help/matlab/math/why-do-random-numbers-repeat-after-startup.html
% https://ww2.mathworks.cn/help/matlab/ref/rng.html
n = 40; % 有多少名同学
mydata = csvread('mydata.csv');%% 参数初始化
T0 = 1000; % 初始温度
T = T0; % 迭代中温度会发生改变,第一次迭代时温度就是T0
maxgen = 500; % 最大迭代次数
Lk = 500; % 每个温度下的迭代次数
alpfa = 0.95; % 温度衰减系数%% 随机生成一个初始解
path0 = randperm(n);
result0 = calculate_ans(path0,mydata); % 计算这一组解对应的标准差%% 定义一些保存中间过程的量,方便输出结果和画图
min_result = result0;
RESULT = zeros(maxgen,1); % 记录每一次外层循环结束后找到的min_result (方便画图)%% 模拟退火过程
for iter = 1 : maxgen % 外循环, 我这里采用的是指定最大迭代次数for i = 1 : Lk % 内循环,在每个温度下开始迭代path1 = gen_new_path(path0); result1 = calculate_ans(path1,mydata); if result1 < result0 path0 = path1; result0 = result1; elsep = exp(-(result1 - result0)/T); % 根据Metropolis准则计算一个概率if rand(1) < p % 生成一个随机数和这个概率比较,如果该随机数小于这个概率path0 = path1; result0 = result1; endend% 判断是否要更新找到的最佳的解if result0 < min_result % 如果当前解更好,则对其进行更新min_result = result0; best_path = path0; endendRESULT(iter) = min_result; % 保存本轮外循环结束后找到的最小的结果T = alpfa*T; % 温度下降
enddisp('最佳的方案是:'); disp(reshape(best_path,4,n/4))
disp('此时最优值是:'); disp(min_result)%% 画出每次迭代后找到的图形
figure
plot(1:maxgen,RESULT,'b-');
xlabel('迭代次数');[~,tmp] = calculate_ans(best_path,mydata) % 前面的~表示不需要第一个返回结果
toc
% calculate_ans.mfunction [ans,tmp] = calculate_ans(path,mydata)n = length(path); % 学生个数nums = n / 4; % 寝室个数path = reshape(path,4,nums); % 每四个人分配到一个寝室tmp = zeros(1,nums); % tmp用来保存每个寝室的共同爱好数for i = 1 : numstmp(i) = get_total_hobby(path(:,i),mydata); % 调用子函数单独计算每个寝室四名同学的共同爱好数end
% ans = std(tmp); % 计算标准差ans = (std(tmp) + 1) / max(tmp);
% ans = (std(tmp) + 1) / mean(tmp);
end
% get_total_hobby.mfunction hobby = get_total_hobby(path,mydata)
% path: 同寝室四名同学的编号
% mydata: 每两个同学之间的共同爱好数hobby = 0;for i = 1 : 4for j = 1:iif i ~= jhobby = hobby+mydata(path(i), path(j));endendend
end
% gen_new_path.mfunction path1 = gen_new_path(path0)% path0: 原来的路径n = length(path0);% 随机选择两种产生新路径的方法p1 = 0.33; % 使用交换法产生新路径的概率p2 = 0.33; % 使用移位法产生新路径的概率r = rand(1); % 随机生成一个[0 1]间均匀分布的随机数if r< p1 % 使用交换法产生新路径 c1 = randi(n); % 生成1-n中的一个随机整数c2 = randi(n); % 生成1-n中的一个随机整数path1 = path0; % 将path0的值赋给path1path1(c1) = path0(c2); %改变path1第c1个位置的元素为path0第c2个位置的元素path1(c2) = path0(c1); %改变path1第c2个位置的元素为path0第c1个位置的元素elseif r < p1+p2 % 使用移位法产生新路径c1 = randi(n); % 生成1-n中的一个随机整数c2 = randi(n); % 生成1-n中的一个随机整数c3 = randi(n); % 生成1-n中的一个随机整数sort_c = sort([c1 c2 c3]); % 对c1 c2 c3从小到大排序c1 = sort_c(1); c2 = sort_c(2); c3 = sort_c(3); % c1 < = c2 <= c3tem1 = path0(1:c1-1);tem2 = path0(c1:c2);tem3 = path0(c2+1:c3);tem4 = path0(c3+1:end);path1 = [tem1 tem3 tem2 tem4];else % 使用倒置法产生新路径c1 = randi(n); % 生成1-n中的一个随机整数c2 = randi(n); % 生成1-n中的一个随机整数if c1>c2 % 如果c1比c2大,就交换c1和c2的值tem = c2;c2 = c1;c1 = tem;endtem1 = path0(1:c1-1);tem2 = path0(c1:c2);tem3 = path0(c2+1:end);path1 = [tem1 fliplr(tem2) tem3]; %矩阵的左右对称翻转 fliplr,上下对称翻转 flipudend
end
五、注意
1.一定能找到最优解吗?
可以利用马尔科夫过程进行证明
2.参数的选择
3.新解的构造
4.算法之间的相互比较
遗传、粒子群、蚁群
