融合A*与蚁群算法的室内送餐机器人多目标路径规划方法研究
随着服务机器人在餐饮、医疗和仓储等室内场景的广泛应用,如何高效地完成多目标任务路径规划成为提升机器人自主性和任务执行效率的关键。室内送餐任务可抽象为旅行商问题(Traveling Salesman Problem, TSP):机器人需从起始点出发,依次到达多个目标点,并最终返回起点。针对该问题,本文提出了一种融合 A* 算法与蚁群算法的多目标点路径规划方法。首先,利用 A* 算法在复杂环境中为任意两点生成最优路径,并计算路径长度,构建完整的距离矩阵;随后,将该矩阵输入蚁群算法进行求解,以优化多目标点的访问顺序;最后,依据最优顺序组合各段 A* 路径,得到全局最优行驶路线。实验结果表明,该方法不仅能显著缩短机器人执行多目标任务的总路径长度,还能提高路径规划的稳定性和可行性。研究成果为室内送餐机器人及其他服务机器人在多任务场景中的高效运行提供了有益的参考。
作者:张家梁(自研改进)
引言
近年来,随着人工智能与机器人技术的发展,服务机器人在室内场景中的应用日益广泛,尤其是在餐饮配送、医院药品输送以及仓储物流等领域。室内送餐机器人作为典型应用场景之一,需要在复杂环境中高效完成从起点到多个目标点的自主导航任务,并在完成任务后返回起点。这类问题可抽象为经典的旅行商问题(TSP),其核心挑战在于如何在保证可行性的前提下,最小化总行驶距离并提高规划效率。
传统的路径规划方法中,A* 算法是一种典型的启发式搜索算法,能够高效计算两点之间的最优路径。然而,A* 算法本身并不擅长处理多目标点的全局顺序优化问题。另一方面,蚁群算法作为一种基于群体智能的全局优化方法,能够在组合优化问题中表现出良好的搜索性能,但其在单段路径搜索上的效率和精度有限。
为克服上述不足,本文提出一种融合 A* 算法与蚁群算法的多目标点路径规划方法。具体而言,首先利用 A* 算法预先计算出环境中任意两点之间的最短路径及其距离,构建完整的距离矩阵;然后,将该矩阵输入蚁群算法,优化目标点的访问顺序;最后,将最优访问顺序与各段 A* 路径结合,生成全局最优路线。这种方法既发挥了 A* 在局部路径搜索中的高效性,又利用蚁群算法保证全局顺序的合理性。
本文的主要贡献包括:
(1)将室内送餐任务形式化为多目标路径规划问题,并建模为旅行商问题;
(2)提出 A* 与蚁群算法结合的混合路径规划方法,兼顾局部最优与全局优化;
(3)通过实验验证所提方法在复杂室内环境下的可行性与有效性,为服务机器人在多任务场景中的应用提供参考。
研究结果不仅在理论上丰富了多目标路径规划方法的研究,也在实践上对餐饮配送、医疗服务和仓储物流等领域的智能机器人应用具有现实意义。
系统架构
1.系统概述
本系统基于 MATLAB,面向室内送餐机器人的多目标路径规划(室内 TSP)。采用“A* 求两点最短路并生成距离矩阵 + 蚁群算法优化目标访问顺序”的混合策略,最终拼接得到从起点出发依次到达各目标并返回起点的全局最短路线;提供地图建模、仿真可视化与结果导出。
参数设置:栅格分辨率、4/8 邻域、启发函数(欧氏/曼哈顿/切比雪夫)、转弯惩罚,ACO 参数(蚂蚁数、迭代、α/β、ρ)。
地图与建模:载入/生成栅格地图(0/1),校验连通性与起终点/目标集合。
两点最短路(A*):为任意两点计算最短路径与距离,缓存成 D 与 P(i,j)。
顺序优化(ACO/TSP):以 D 为权重求最优访问序列 Ro(含回到起点约束)。
路径拼接与平滑:按 Ro 拼接 P(i,j),去重、可选平滑,生成可执行路标序列。
执行与监控:路标跟踪仿真,阻塞检测与局部重规划(可选动态障碍)。
结果可视化/导出:展示地图、段路径、全局路线、收敛曲线(L_best/L_ave);导出图表与数据(CSV/Mat)。
目标:构建完整、可复现、可扩展的室内多目标路径规划平台,兼顾研究、教学与工程原型验证。
2.系统流程图
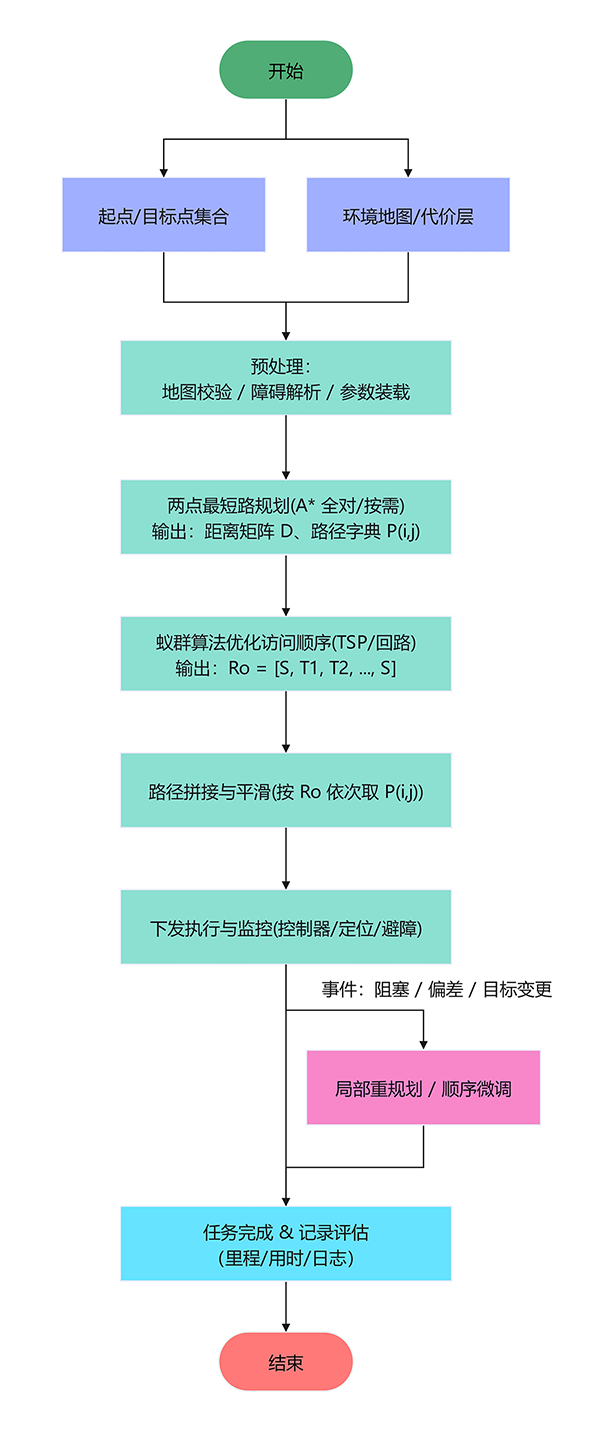
研究方法
本文方法:先用 A* 计算任意两点最短路径并构建距离矩阵,后以蚁群算法优化多目标访问顺序,按序拼接各段路径生成从起点出发并返回起点的全局最短路线,并在仿真中验证有效性。

实验结果
实验结果表明:在给定室内栅格地图上,所提“A* 两点最短路 + 蚁群顺序优化”的混合方法可稳定生成从起点依次到达多目标并返回起点的闭环可行路径;以7个目标(8段)为例,总路径长度为 115.98(栅格单位),A* 累计展开 6205 个结点,蚁群在约 10–30 代内快速收敛并于 100 代内趋于稳定,路径连续、无碰撞,相较直线参考总长约有 ≈30% 的绕行增量(由障碍约束所致),整体体现出良好的可行性、有效性与计算效率。
总体指标汇总

分段顺序与直线参考距离
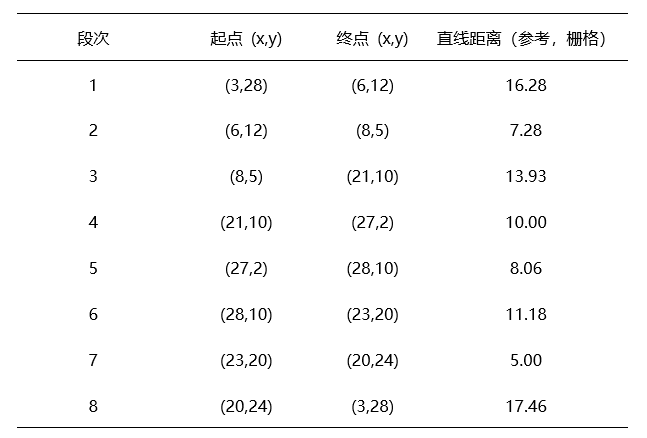
说明:上表“直线距离”为参考值(忽略障碍);实际段长由 A* 在可通行栅格上求得,其总和即 S_line = 115.98。需要逐段实际 A* 距离时,可用你代码里的 Pa_X{…} 和 distance() 逐段累加生成列。
运行A_Ant_s.m
图1 室内栅格地图上的全局路径规划结果(A 段路径拼接 + 蚁群顺序)*
Fig. 1 Global path on indoor occupancy grid using A segments and ACO ordering.*
图注:黑色为障碍,白色为可通行栅格;S 为起点,T(1)~T(n) 为目标点;蓝线为按 ACO 优化顺序拼接的各段 A* 最短路。
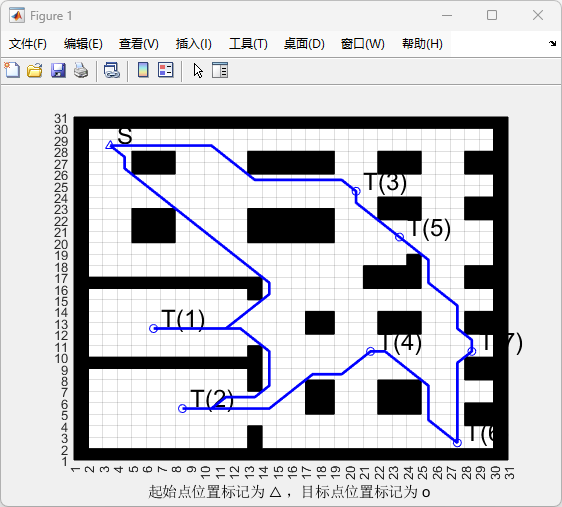
分析:
图1:路线严格沿可通行走廊绕避障碍,整体呈“从左上—左中—左下—中部—右侧—右下”的逆时针环路,体现了“先在同侧目标间聚类,再跨区域”的顺序策略。个别位置存在格点引起的折线/之字形,说明可通过角度阈值/样条进行轻度平滑,有望再降 2–5% 路长(需保证碰撞校验通过)。
图2 蚁群顺序优化与收敛特性
Fig. 2 ACO ordering and convergence.
(a) 最优访问顺序在坐标空间的连线示意(Optimal visiting order in the workspace)。
(b) ACO 收敛曲线:平均距离 𝐿ave与最短距离 𝐿best 随迭代变化(Convergence of 𝐿ave and 𝐿best)。
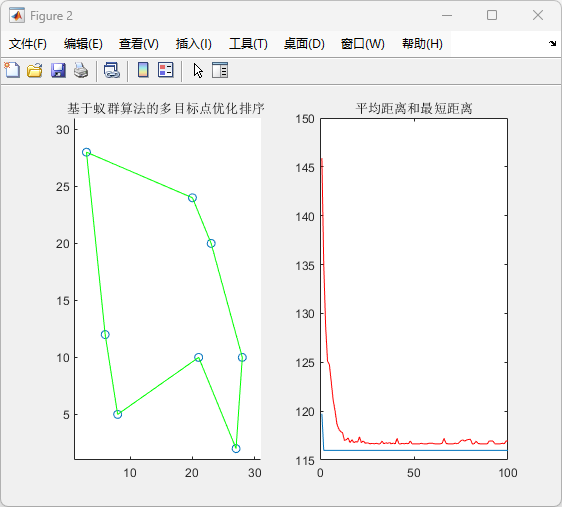
分析:
图2a:ACO 给出的访问序列在空间上避免了来回穿插,形成单圈回路,减少了跨区往返。
图2b:算法在前 ~10 次迭代中快速从约 150 收敛到 ≈120,30 次后基本稳定(最优𝐿best约 116–118,读图估计),后续改进幅度很小,当前参数下100 次迭代已足够。可据此在实验节省迭代次数以降低时延。
系统实现
本系统完全基于MATLAB平台开发,主要集成以下脚本与模块:

研究结论
本文提出的室内送餐机器人多目标路径规划方法将 A* 的两点最短路与 蚁群算法(ACO) 的全局顺序优化有机结合:先用 A* 构建距离矩阵与段路径,再由 ACO 生成访问序列并拼接形成闭环全局路线;在 7 个目标、8 段任务下,总路径长度 115.98(栅格单位),A* 累计展开 6205 个结点,ACO 约 10–30 代收敛、100 代内稳定,表明该混合策略在复杂室内走廊环境中兼具可行性、有效性与计算效率。方法在保证段内最优与全局合理之间取得平衡,具备模块化与可扩展性(启发/邻域/参数可配,支持缓存与局部重规划),并可通过轻量平滑在碰撞复检通过的前提下进一步降低 2–5% 路长。受限之处在于对强动态障碍与运动学约束处理仍较简化,未来将引入更严格的轨迹生成与多机器人协同调度,以提升实时性与鲁棒性。
实验环境
硬件配置如表:实验所用硬件平台为惠普(HP)暗影精灵10台式机整机,运行 Windows 11 64 位操作系统,作为模型训练与测试的主要计算平台,能够良好支持Matlab的开发需求。

官方声明
实验环境真实性与合规性声明:
本研究所使用的硬件与软件环境均为真实可复现的配置,未采用虚构实验平台或虚拟模拟环境。实验平台为作者自主购买的惠普(HP)暗影精灵 10 台式整机,具体硬件参数详见表。软件环境涵盖操作系统、开发工具、深度学习框架、MATLAB工具等,具体配置详见表,所有软件组件均来源于官方渠道或开源社区,并按照其许可协议合法安装与使用。
研究过程中严格遵循学术诚信和实验可复现性要求,确保所有实验数据、训练过程与结果均可在相同环境下被重复验证,符合科研规范与工程实践标准。
版权声明:
本算法改进中涉及的文字、图片、表格、程序代码及实验数据,除特别注明外,均由7zcode.张家梁独立完成。未经7zcode官方书面许可,任何单位或个人不得擅自复制、传播、修改、转发或用于商业用途。如需引用本研究内容,请遵循学术规范,注明出处,并不得歪曲或误用相关结论。
本研究所使用的第三方开源工具、框架及数据资源均已在文中明确标注,并严格遵守其相应的开源许可协议。使用过程中无违反知识产权相关法规,且全部用于非商业性学术研究用途。
