当前位置：首页 > news >正文

【记录】初赛复习 Day2 Day3（内附2024S第一轮难题详解）

news 2025/9/17 8:29:41

我自己复习初赛的记录，是这个网站：

信息学奥赛-NOIP-少儿编程培训-有道小图灵 (youdao.com)

昨天去眼科医院了，两天一起写。

这篇主要以做 s 模拟为主，会写一些我自己的独特方法。

1.S组-基础知识与编程环境

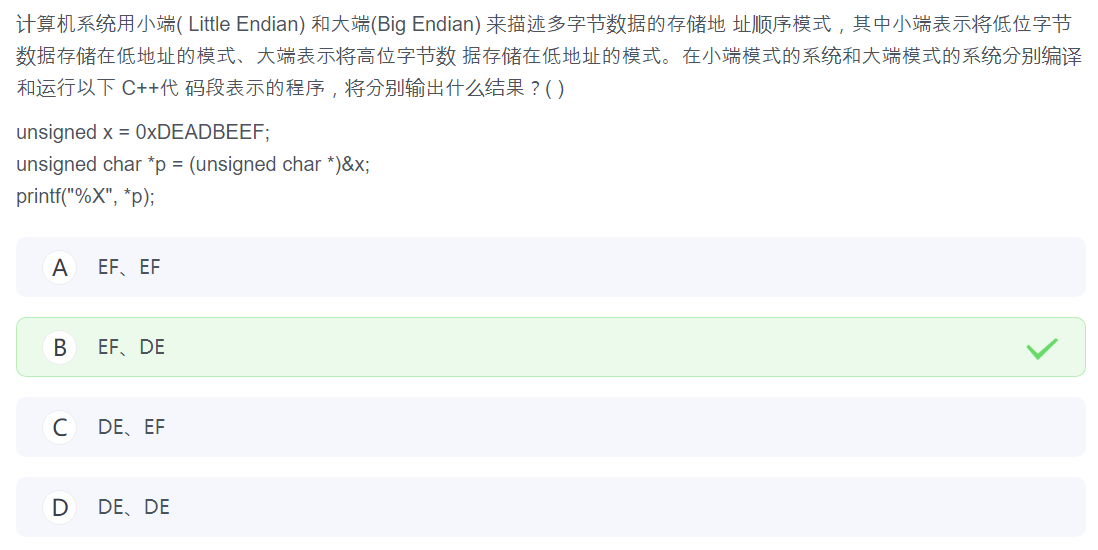
乱蒙的，对于我这种学表面计算机的根本看不懂。

（%X 就是输出十六进制）

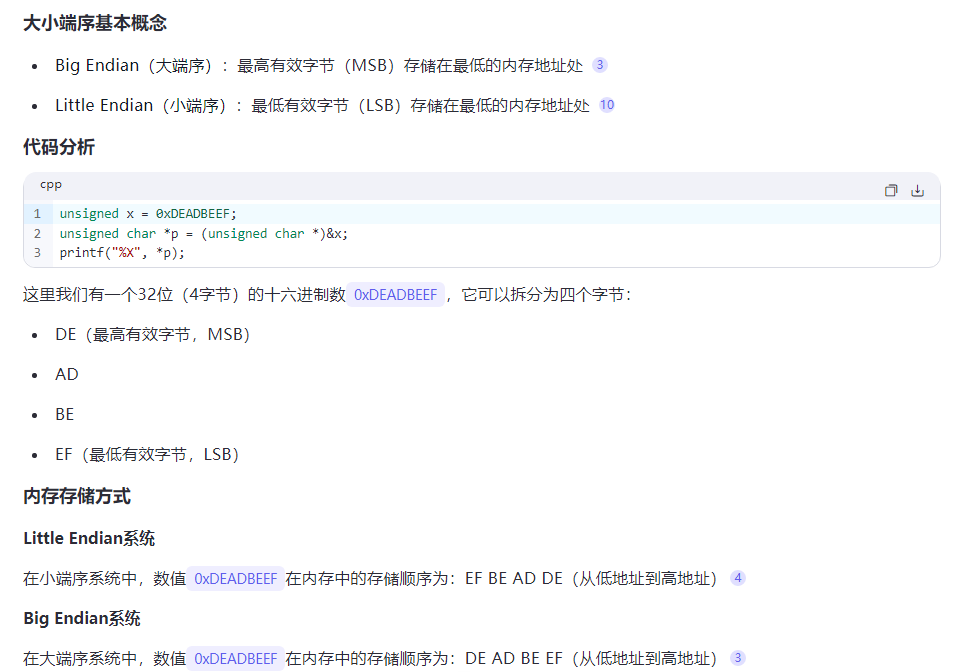
最接近秒表计时的时长是 real 时间，因为 real 时间表示程序从开始到结束的总时间，

包括用户模式时间 (user 时间) 和内核模式时间 (sys 时间) 所需的总时间。

（无脑选最长，反正不会闲着没事给你加起来）

常用 Linux 命令：

历史人物：

（感觉很少教材说上面这位老兄）

文件命令：

g++ 编译命令在 -o 后跟输出名称，即

g++ 源文件名 -o 输出名称

或者

g++ -o 输出名称源文件名

2.S组-C 程序设计

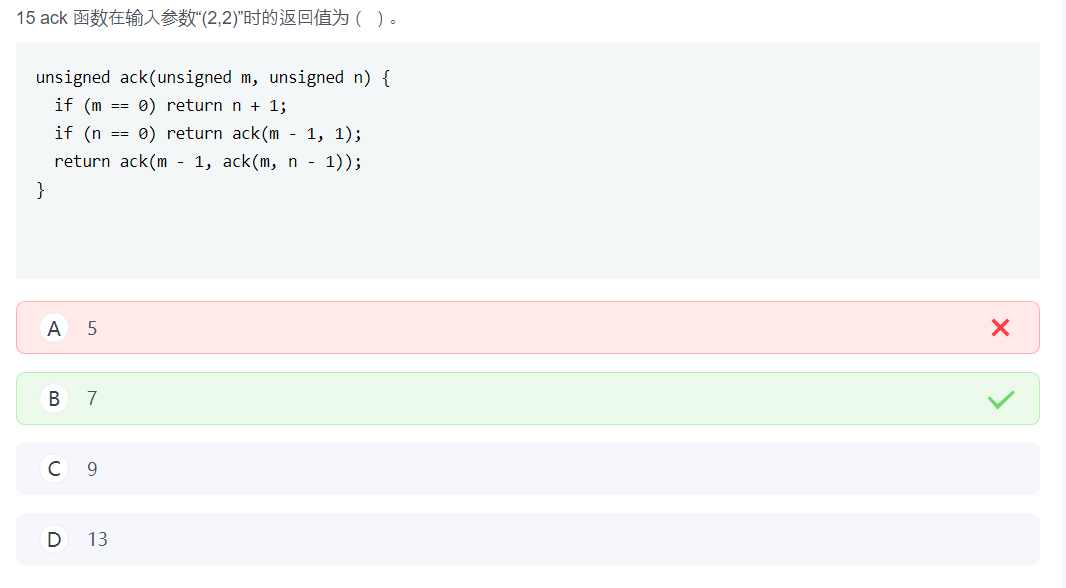
这种嵌套的递归还是打表吧，不然代着代着就混了。

bool 输出真假，，，虽然我真正编码的时候从来没用过。

3.2024年CSP提高级第一轮认证

7.

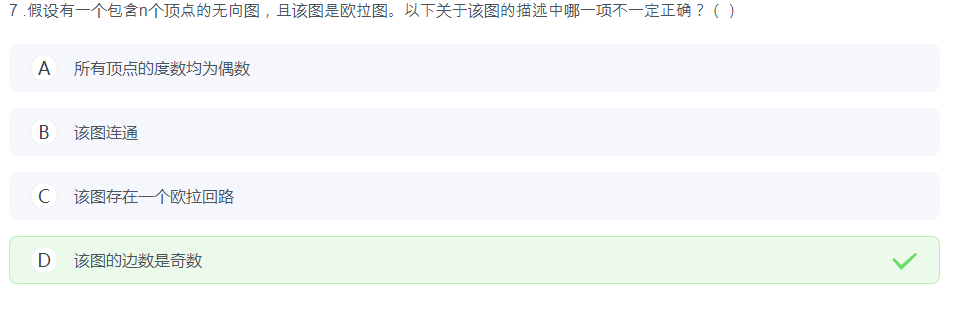
错题，因为欧拉图只要求所有边连通，并不要求所有点连通，因此对 B 项存疑。

（可能有那种单个点不连边的）

10.

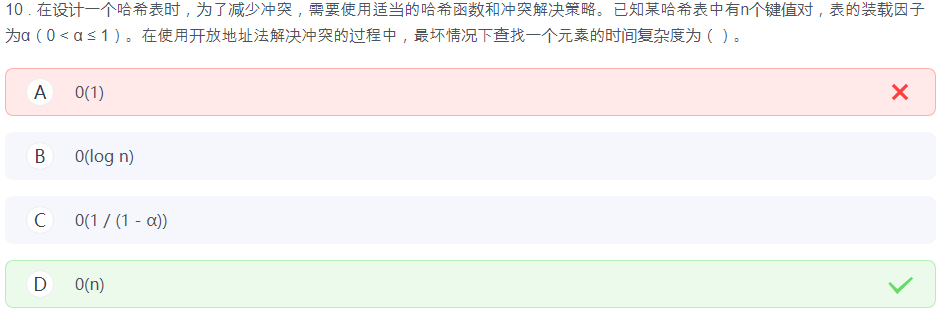
为什么是O(n)？

当 α = 1（表完全满）时，m = n，时间复杂度为 O(n)
当 α = 0.5 时，m = 2n，时间复杂度为 O(2n) = O(n)
当 α 很小（如 α = 0.1）时，m = 10n，时间复杂度为 O(10n) = O(n)

（提一嘴，链地址方法最坏时间复杂度也是 O(N)，不过和装载因子没关系）

12.

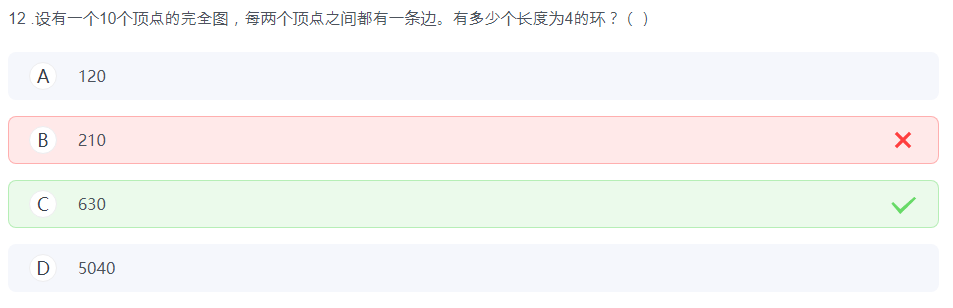
完全图是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连。

对于选定的 4 个顶点，计算它们能形成多少个不同的长度为 4 的环。

注意环上的点是有顺序的，但没有方向。所以有：

4 个顶点可以有 4! = 24 种排列方式
但每个环会被计算 8 次（4 个可能的起点 × 2 个方向：顺时针和逆时针）
所以不同的环数量 = 24 / 8 = 3

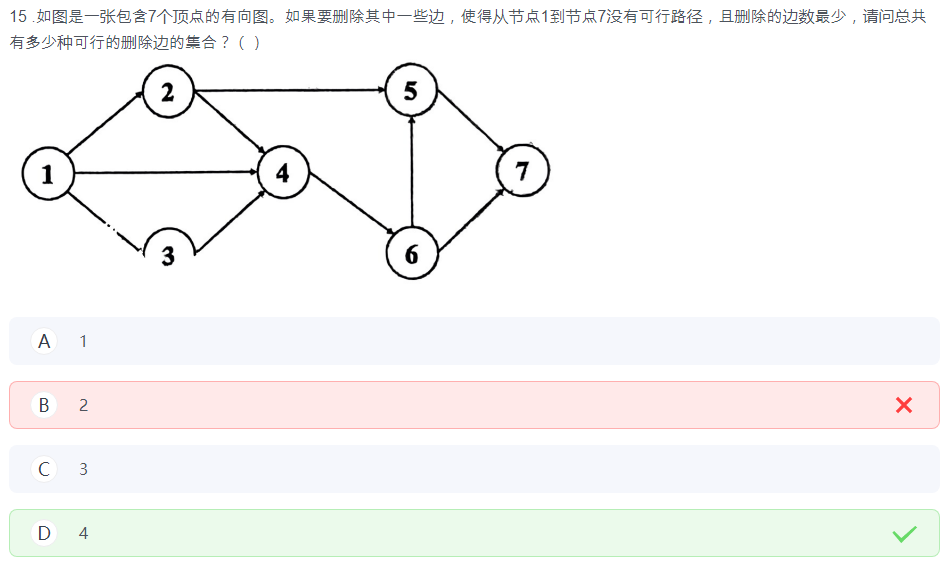
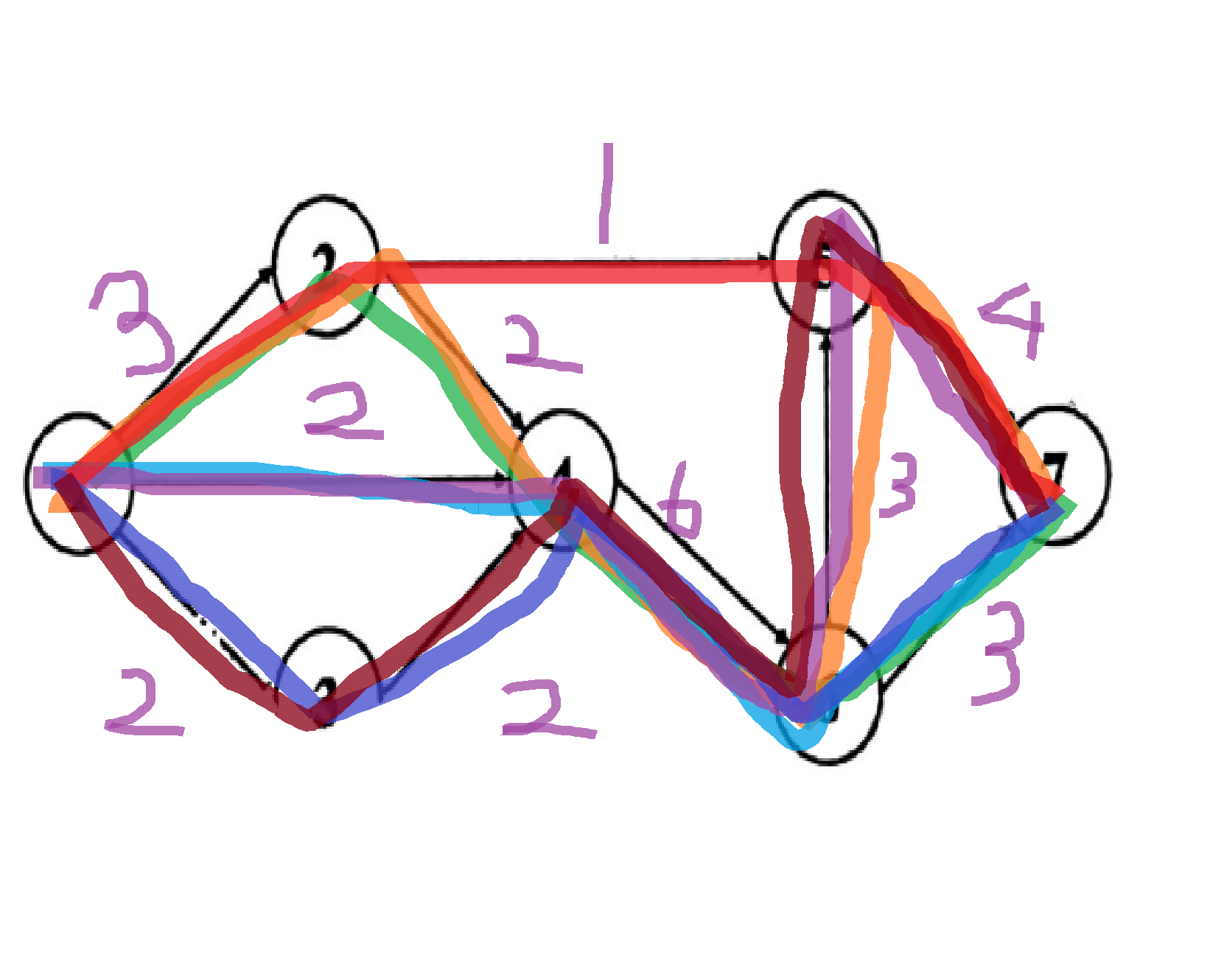
（用不同颜色标出不同的路径，标出每条边路径的数量）

找两条数字加起来大于等于所有路径数量 7 的边。

这个故事告诉我们上考场多带点颜色笔。

16.

#include <iostream>
using namespace std;const int N = 1000;
int c[N];int logic(int x, int y) {return (x & y) ^ ((x ^ y) | (~x & y));
}// Renamed from 'generate' to avoid conflict with std::generate
void generate_data(int a, int b, int *c) {for (int i = 0; i < b; i++) {c[i] = logic(a, i) % (b + 1);}
}void recursion(int depth, int *arr, int size) {if (depth <= 0 || size <= 1) return;int pivot = arr[0];int i = 0, j = size - 1;while (i <= j) {while (arr[i] < pivot) i++;while (arr[j] > pivot) j--;if (i <= j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;i++; j--;}}recursion(depth - 1, arr, j + 1);recursion(depth - 1, arr + i, size - i);
}int main() {int a, b, d;cin >> a >> b >> d;generate_data(a, b, c);recursion(d, c, b);for (int i = 0; i < b; ++i) cout << c[i] << " ";cout << endl;return 0;
}

logic ：逻辑 generate：生成 recursion：递归

看到深井 logic 函数别急，先打表：

y \ 位运算（x：101，~x = 010）	x & y	x ^ y	~x & y	总结果
0（000）	000	101	000	000 ^ (101 \| 000) = 101
1（001）	001	100	000	001 ^ (100 \| 000) = 101
2（010）	000	111	010	000 ^ (111 \| 010) = 111
3（011）	001	110	010	001 ^ (110 \| 010) = 111
4（100）	100	001	000	100 ^ (001 \| 000) = 101

可以发现当输入是 5 5 1 时，c 数组是 5 5 1 1 5。

然后看看那个 recursion 递归函数，我第一眼看成归并排序了，但实际上是类快排。

哎，那就看看区别吧：

所以 recursion 函数是快速排序算法，但它只会进行 depth 轮排序。

16 题发现 d $\geq$ b，也就是快排的递归次数大于等于数组大小，包有序的，T。

17 题发现 d = 1，也就是只递归一次。

那么 5 5 1 1 5 开始递归时，a[0] = 5，当 i = 0，j = 3 的时候会停下。

交换第 1 个和第 3 个，得到 5 1 1 5 5。也就是输出 5 1 1 5 5，F。

18 题 recursion 函数时间复杂度是 depth * size，也就是 O(db)，F。

19 题经过我们打完表发现，这深井函数就是按位或，B。

20 题先求出 10 是 1010，然后找找 1 到 100 里有哪个数与 10 按位或最大。

比如说先看看 99 的二进制：1100011，发现或完后超过了 100，再模就变得很小了。

那没办法，看看 95（99 减掉 3 再减 1）：1011111，发现只能这样了，C。

17.

#include <iostream>
#include <string>
using namespace std;const int P = 998244353;
const int N = 10010;  // Fixed: 1e4+10 → 10010 (integer literal)
const int M = 20;
int n, m;
string s;
int dp[1 << M];int solve() {dp[0] = 1;for (int i = 0; i < n; ++i) {for (int j = (1 << (m - 1)) - 1; j >= 0; --j) {int k = (j << 1) | (s[i] - '0');if (j != 0 || s[i] == '1') {dp[k] = (dp[k] + dp[j]) % P;}}}int ans = 0;for (int i = 0; i < (1 << m); ++i) {ans = (ans + 1LL * i * dp[i]) % P;}return ans;
}int solve2() {int ans = 0;for (int i = 0; i < (1 << n); ++i) {int cnt = 0;int num = 0;for (int j = 0; j < n; ++j) {if (i & (1 << j)) {num = num * 2 + (s[j] - '0');cnt++;}}if (cnt <= m) {ans = (ans + num) % P;}}return ans;
}int main() {cin >> n >> m;cin >> s;if (n <= 20) {cout << solve2() << endl;}cout << solve() << endl;return 0;
}

其实这道题最大的问题是看不懂这俩私人东西在干什么。

先别急着代入，看出来 solve 函数是一个类似背包的东西，

好像是求 s 中长度为 m 的子段权值和。

就比如这个 11 2 10000000001，能统计在内的有 1，10，11（不含前导零）。

solve2 发现枚举的会计入答案的 i，就是长度为 n 的 01 串中有不超过 m 个的 1。

然后把这些为 1 的位对应到原来的 s 上，计算权值。

比如 11 2 10000000001，我枚举 i 是 10000000000，那我的权值就是 1。

枚举 i 是 10000000010，权值就是 10（二进制），也就是 2。

枚举 i 是 10000000001，权值就是 11（二进制），也就是 3。

枚举 i 是 00000000001，权值就是 1（二进制），也就是 1。

枚举 i 是 00000000011，权值就是 01（二进制），也就是 1。

那么能统计在内的有 1，01，10，11。

现在再来看题：

21 不讲了，一眼 T。

22 发现 s 的子序列中：1 有 2 个，01 有 9 个，10 有 9 个，11 有 1 个。

solve2 = 2 * 1 + 9 * 1 + 9 * 2 + 3 * 1 = 32，solve = 2 * 1 + 9 * 2 + 3 * 1 = 23，T。

23 有点难，首先我们知道肯定是全为 1 的 s 得出的值最大，m = 10 的时候最大。

那么这个时候的 solve 就等于： $\sum_{i=1}^{n}\binom{n}{i}(2^i-1)$

（i 是表示当前要选多少个 1）

$=\sum_{i=1}^{n}\binom{n}{i}2^i-\sum_{i=1}^{n}\binom{n}{i}$

哎这俩东西看着像二项式定理： $(a+b)^n=\sum_{i=0}^{n}\binom{n}{i}a^{n-i}b^i$ 啊。

$=\sum_{i=1}^{n}\binom{n}{i}2^i*1^{n-i}-\sum_{i=1}^{n}\binom{n}{i}*1^{n-i}$

$=(2+1)^n-(1+1)^n$

$=3^{10}-2^{10}$

不用算了这俩肯定小于 $4^{10}$ ，T。

24 简单，只要不存在 01 子串就好。

0000000000

0000000001

0000000011

0000000111

0000001111

0000011111

0000111111

0001111111

0011111111

0111111111

1111111111

共 11 个，B。

25 炒冷饭，将 n = 6 代入 23 求出来的公式：

$=(2+1)^n-(1+1)^n$

$=3^{6}-2^{6}$

也不大，一算发现是 665，C。

26 想要差值最大，那么就要含前导零的子串尽可能多，考虑 01111111。

01 有 7 个，1 * 7 = 7。

011 有 $\binom{7}{2}=21$ 个，3 * 21 = 63。

0111 有 $\binom{7}{3}=35$ 个，7 * 35 = 245。

01111 有 $\binom{7}{4}=35$ 个，15 * 35 = 525。

011111 有 $\binom{7}{5}=21$ 个，31 * 21 = 651。

0111111 有 $\binom{7}{6}=7$ 个，63 * 7 = 441。

01111111 有 1 个，127 * 1 = 127。

7 + 63 + 245 + 525 + 651 + 441 + 127 = 2059，选 C。

18.

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;const int maxn = 1000005;  // Fixed: 1000000+5 → 1000005
const int P1 = 998244353;
const int P2 = 1000000007;
const int B1 = 2;
const int B2 = 31;
const int k1 = 0;  // Fixed: renamed from K1 to k1 (lowercase)
const int k2 = 13; // Fixed: renamed from K2 to k2 (lowercase)typedef long long ll;int n;
bool p[maxn];
int p1[maxn], p2[maxn];struct H {int h1, h2, l;H(bool b = false) {h1 = b + k1;h2 = b + k2;l = 1;}H operator+(const H& h) const {H hh;hh.l = l + h.l;hh.h1 = (1LL * h1 * p1[h.l] + h.h1) % P1;hh.h2 = (1LL * h2 * p2[h.l] + h.h2) % P2;return hh;}bool operator==(const H& h) const {return l == h.l && h1 == h.h1 && h2 == h.h2;}bool operator<(const H& h) const {if (l != h.l) return l < h.l;else if (h1 != h.h1) return h1 < h.h1;else return h2 < h.h2;}
} h[maxn];void init() {memset(p, 1, sizeof(p));p[0] = p[1] = false;p1[0] = p2[0] = 1;for (int i = 1; i <= n; ++i) {p1[i] = (1LL * B1 * p1[i-1]) % P1;p2[i] = (1LL * B2 * p2[i-1]) % P2;  // Fixed: was % p2 (array)if (!p[i]) continue;for (int j = 2 * i; j <= n; j += i) {p[j] = false;}}
}int solve() {for (int i = n; i > 0; --i) {h[i] = H(p[i]);if (2 * i + 1 <= n) {h[i] = h[2 * i] + h[i] + h[2 * i + 1];} else if (2 * i <= n) {h[i] = h[2 * i] + h[i];}}cout << h[1].h1 << endl;sort(h + 1, h + n + 1);int m = unique(h + 1, h + n + 1) - (h + 1);return m;
}int main() {cin >> n;init();cout << solve() << endl;return 0;
}

这个深井初始化：

H(bool b = false) {h1 = b + k1;h2 = b + k2;l = 1;}

和这样没区别：

H(bool b) {h1 = b + k1;h2 = b + k2;l = 1;}

深井模拟题。

init 函数是埃氏筛，时间复杂度 O(n log log n)。

其他就是莫名其妙的哈希。

27 正确，埃氏筛跑的飞起，最慢的就只有快排 O(n log n) 了。

28 错误，刚刚说过，最慢的是快排。

29 正确，没啥好说的。

30 C，送的。

31 发现第一行是输出 h[1].h1，直接模拟：

10 {0,13,1}
9 {0,13,1}
8 {0,13,1}
7 {1,14,1}
6 {0,13,1}
5 {1,14,1} = {1, ,2}
4 {0,13,1} = {0, ,2} = {0, , 3}
3 {1, 14, 1} = {1, ,2} = {3, ,3}
2{1, , 1} = {1, , 4} = {5, ,6}
1{0, ,1} = {10, , 7} = {83, , 10}

（因为 h2 没啥卵用，这里就只写 h1）

只要你不算错，就知道选 A。

32 问我们 n = 16 的 h 数组有多少个不同的，再模拟，这次更简单：

16 {0,13,1}
15 {0,13,1}
14 {0,13,1}
13 {1,14,1}
12 {0,13,1}
11 {1,14,1}
10 {0,13,1}
9 {0,13,1}
8 {0,13,1} = {0, 2} = 3
7 {0,13,1} = 合+质+合= 4
6 {0,13,1} = 合+合+质 = 5
5 {0,13,1} = 合+质+质 = 6
4 {0,13,1} = 7
3 {0,13,1} = 8
2 {0,13,1} = 9
1 {0,13,1} = 10

我讲一下我的抽象写法，因为 8765 的 2n 和 2n + 1 都是最基础的 h1 h2 l。

所以只要看组成部分就好，组成不同那就是不同的。

4321 就更不用说了，不知道什么牛鬼蛇神拼一起，能一样就有鬼了。

选 C。

19.

（序列合并）有两个长度为N的单调不降序列 A 和 B，序列的每个元素都是小于 10^9 的非负整数。在 A 和 B 中各取一个数相加可以得到 N^2 个和，求其中第 K 小的和。上述参数满足 N <= 10^5 和 1 <= K <= N^2。

#include <iostream>
using namespace std;const int maxn = 100005;int n;
long long k;
int a[maxn], b[maxn];int* upper_bound(int* a, int* an, int ai) {int l = 0, r = _________1_________;while (l < r) {int mid = (l + r) >> 1;if (______2_______) {r = mid;} else {l = mid + 1;}}return _______3______;
}long long get_rank(int sum) {long long rank = 0;for (int i = 0; i < n; ++i) {rank += upper_bound(b, b + n, sum - a[i]) - b;}return rank;
}int solve() {int l = 0, r = _______4______;while (l < r) {int mid = ((long long)l + r) >> 1;if (______5______) {l = mid + 1;} else {r = mid;}}return l;
}int main() {cin >> n >> k;for (int i = 0; i < n; ++i) {cin >> a[i];}for (int i = 0; i < n; ++i) {cin >> b[i];}cout << solve() << endl;return 0;
}

喜闻乐见小二分。

二分最恶心的是边界，而这道题是边界集毒瘤之大成者。

虽然题面已经说得很清楚了，但我们还是得理一下每个函数要干什么：

solve：

二分范围：l = 0（最小可能和），r = a[n-1] + b[n-1]（最大可能和）
计算中点 mid
如果 get_rank(mid) < k，说明 mid 太小，需要增大 → l = mid + 1
否则，说明 mid 可能太大或正好 → r = mid
最终 l 就是第 k 小的和

get_rank：

功能：计算有多少对 (a[i], b[j]) 满足 a[i] + b[j] <= sum
原理：
1. 对每个 a[i]，计算sum - a[i]
2. 在数组 b 中查找第一个大于 sum - a[i] 的元素位置
3. upper_bound(...) - b得到 b 中小于等于 sum - a[i] 的元素个数
4. 将所有 a[i] 对应的计数相加，得到满足条件的总对数

upper_bound：

功能：在已排序的数组 b 中查找第一个大于 ai 的元素的位置
原理：二分查找实现
- 当 a[mid] <= ai 时，说明 mid 及左边都不满足条件，需要向右查找
- 最终返回指向第一个大于 ai 的元素的指针

仔细分析过答案就已经很明显了，哪个神人写的的五个 A。

20.

(次短路）已知一个有 n 个点 m 条边的有向图 G，并且给定图中的两个点 s 和 t，求次短路（长度严格大于最短路的最短路径）。如果不存在，输出一行 “-1”。如果存在，输出两行，第一行表示次短路的长度，第二行表示次短路的一个方案。

#include <cstdio>
#include <queue>
#include <utility>
#include <cstring>
using namespace std;const int maxn = 200010;  // Fixed: 2e5+10 → 200010
const int maxm = 1000010; // Fixed: 1e6+10 → 1000010
const int inf = 522133279;int n, m, s, t;
int head[maxn], nxt[maxm], to[maxm], w[maxm], tot = 1;
int dis[maxn << 1], *dis2;
int pre[maxn << 1], *pre2;
bool vis[maxn << 1];void add(int a, int b, int c) {++tot;nxt[tot] = head[a];to[tot] = b;w[tot] = c;head[a] = tot;
}bool upd(int a, int b, int d, priority_queue<pair<int, int>>& q) {if (d >= dis[b]) return false;if (b < n) _________1_______;q.push(________2_______);dis[b] = d;pre[b] = a;return true;
}void solve() {priority_queue<pair<int, int>> q;q.push(make_pair(0, s));memset(dis, _______3______, sizeof(dis));memset(pre, -1, sizeof(pre));dis2 = dis + n;pre2 = pre + n;dis[s] = 0;while (!q.empty()) {int aa = q.top().second;q.pop();if (vis[aa]) continue;vis[aa] = true;int a = aa % n;for (int e = head[a]; e; e = nxt[e]) {int b = to[e], c = w[e];if (aa < n) {if (!upd(a, b, dis[a] + c, q))_____4______;} else {upd(n + a, n + b, dis2[a] + c, q);}}}
}void out(int a) {if (a != s) {if (a < n) out(pre[a]);else out(______5_______);}printf("%d%c", a % n + 1, " \n"[a == n + t]);
}int main() {scanf("%d%d%d%d", &n, &m, &s, &t);s--, t--;for (int i = 0; i < m; ++i) {int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a - 1, b - 1, c);}solve();if (dis2[t] == inf) {puts("-1");} else {printf("%d\n", dis2[t]);out(n + t);}return 0;
}

也妹学过求次短路啊，我没法讲了，给你们看看注释代码：

（AI 太好用了你们知道吗）

#include <cstdio>
#include <queue>
#include <utility>
#include <cstring>
using namespace std;// 常量定义
const int maxn = 200010;  // 最大节点数（200000+10）
const int maxm = 1000010; // 最大边数（1000000+10）
const int inf = 522133279; // 无穷大值，用于初始化距离数组// 全局变量
int n, m, s, t; // 节点数、边数、起点、终点
int head[maxn], nxt[maxm], to[maxm], w[maxm], tot = 1; // 邻接表存储图
// head[i]：以i为起点的最后一条边的编号
// nxt[i]：编号为i的边的下一条边的编号
// to[i]：编号为i的边的终点
// w[i]：编号为i的边的权重
// tot：边的计数器（从1开始）// 距离数组和前驱数组（双层结构）
int dis[maxn << 1], *dis2; // dis[0..n-1]：最短距离；dis[n..2n-1]：次短距离
int pre[maxn << 1], *pre2; // pre[0..n-1]：最短路前驱；pre[n..2n-1]：次短路前驱
bool vis[maxn << 1];       // 标记节点是否已处理/*** 添加一条有向边* @param a 起点* @param b 终点* @param c 边的权重*/
void add(int a, int b, int c) {++tot;              // 边计数器增加nxt[tot] = head[a]; // 新边指向以a为起点的前一条边to[tot] = b;        // 设置边的终点w[tot] = c;         // 设置边的权重head[a] = tot;      // 更新以a为起点的最后一条边
}/*** 更新节点的距离（核心函数）* @param a 当前节点* @param b 目标节点* @param d 新的距离值* @param q 优先队列* @return 是否成功更新*/
bool upd(int a, int b, int d, priority_queue<pair<int, int>>& q) {// 如果新距离不小于当前记录的距离，则无需更新if (d >= dis[b]) return false;// 如果目标节点在第一层（最短路层）if (b < n) // 将当前最短路降级为次短路（关键步骤：保持次短路的正确性），因为当前的可以被 d 更新upd(pre[b], n + b, dis[b], q);// 将新距离加入优先队列（使用负值实现小顶堆）q.push(make_pair(-d, b));// 更新距离和前驱dis[b] = d;pre[b] = a;return true;
}/*** 求解次短路*/
void solve() {priority_queue<pair<int, int>> q; // 优先队列，用于Dijkstra算法q.push(make_pair(0, s));          // 将起点加入队列// 初始化距离数组为无穷大（0x1f近似于INT_MAX/2）memset(dis, 0x1f, sizeof(dis));// 初始化前驱数组为-1（表示无前驱）memset(pre, -1, sizeof(pre));// 设置次短路层的指针（偏移n）dis2 = dis + n;pre2 = pre + n;// 起点的最短距离为0dis[s] = 0;while (!q.empty()) {int aa = q.top().second; // 取出当前距离最小的节点q.pop();// 如果该节点已被处理过，则跳过if (vis[aa]) continue;vis[aa] = true; // 标记为已处理int a = aa % n; // 获取实际节点编号（去除层信息）// 遍历从a出发的所有边for (int e = head[a]; e; e = nxt[e]) {int b = to[e], c = w[e]; // b为邻居节点，c为边权// 如果当前节点在第一层（最短路层）if (aa < n) {// 尝试更新最短路if (!upd(a, b, dis[a] + c, q))// 如果无法更新最短路，则尝试更新次短路upd(a, n + b, dis[a] + c, q);} // 如果当前节点在第二层（次短路层）else {// 只能更新次短路层upd(n + a, n + b, dis2[a] + c, q);}}}
}/*** 输出路径* @param a 当前节点（可能在第一层或第二层）*/
void out(int a) {// 如果不是起点，继续递归输出前驱if (a != s) {// 如果在第一层（最短路层）if (a < n) out(pre[a]);      // 递归输出最短路前驱// 如果在第二层（次短路层）else out(pre2[a % n]); // 递归输出次短路前驱}// 输出当前节点（转换为1-based索引）// 如果是终点(n+t)，则输出换行，否则输出空格printf("%d%c", a % n + 1, " \n"[a == n + t]);
}int main() {// 读入节点数、边数、起点、终点scanf("%d%d%d%d", &n, &m, &s, &t);s--, t--; // 转换为0-based索引// 读入所有边for (int i = 0; i < m; ++i) {int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a - 1, b - 1, c); // 转换为0-based索引}solve(); // 求解次短路// 如果终点的次短路不存在if (dis2[t] == inf) {puts("-1");} // 如果存在次短路else {printf("%d\n", dis2[t]); // 输出次短路长度out(n + t);              // 输出次短路路径}return 0;
}