计算机视觉 - 对比学习（下）不用负样本 BYOL + SimSiam 融合Transformer MoCo-v3 + DINO

对比学习论文综述【论文精读】

对比学习论文综述【论文精读】笔记

        自监督学习，特别是对比学习，如何在不使用负样本的情况下避免模型坍塌（Collapse）？本文深入精读BYOL、SimSiam、MoCo-v3及DINO等里程碑式论文，剖析了“停止梯度”（Stop-Gradient）、自蒸馏（Self-Distillation）等核心机制的工作原理。我们将探讨Batch Normalization是否扮演了“隐式负样本”的角色，并揭示ViT架构下自监督训练的不稳定性问题及其解决方案。最后，通过对不同模型在分类与下游任务上的性能对比，为您提供一幅通往更智能、更简洁表征学习之路的清晰路线图。

目录

第三阶段：不用负样本

3.1 BYOL 在线网络和目标网络

3.2 SimSiam 简化的 总结性的工作

第四阶段：融合Transformer （ViT出来之后）

4.1 MoCo-v3

4.2 DINO 自蒸馏 Self-distillation with no labels

---

第三阶段：不用负样本

3.1 BYOL 在线网络和目标网络

Bootstrap Your Own Latent A New Approach to Self-Supervised Learning

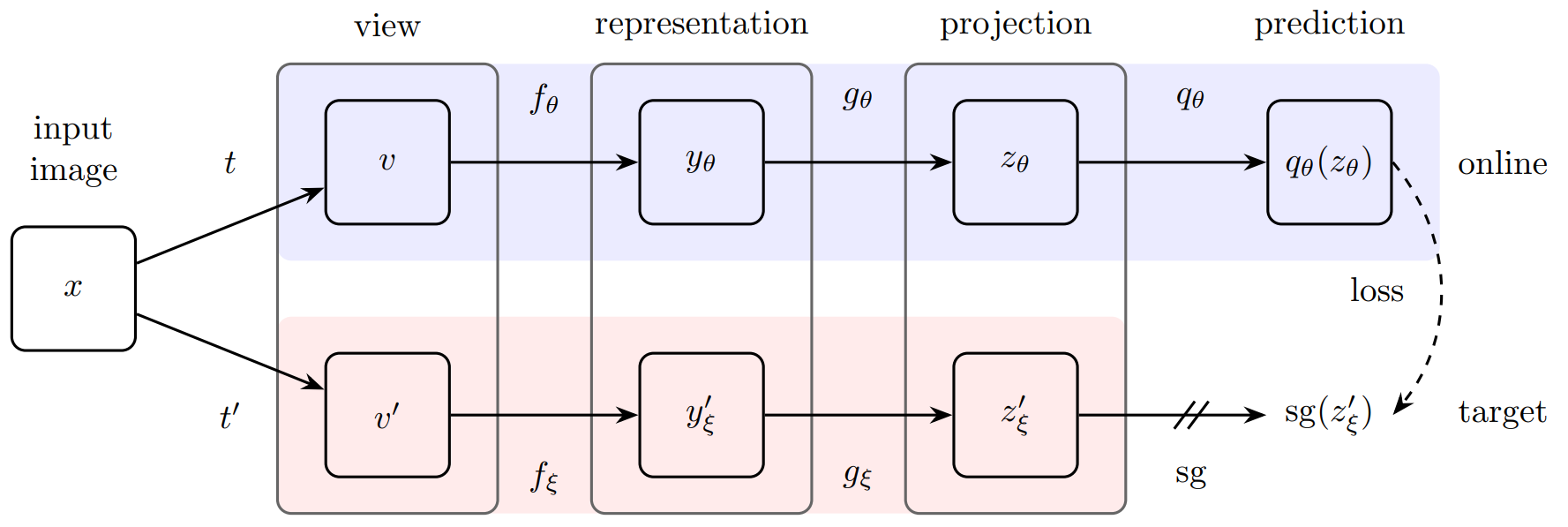
BYOL包含两个神经网络：在线网络（Online Network） 和 目标网络（Target Network）。

1. 网络结构：

   • 在线网络（θ）： 包含三个部分：编码器f_θ、投影头 g_θ 和预测头 q_θ。这个网络通过梯度下降进行更新。

   • 目标网络（ξ）： 与在线网络结构相同（编码器 f_ξ、投影头 g_ξ），但没有预测头。它的参数不是通过梯度更新，而是在线网络参数的指数移动平均（EMA）： ξ ← τξ + (1-τ)θ，其中 τ 是一个接近1的动量系数（如0.99）借鉴MoCo思想。

2. 训练流程：

   • Step 1: 对一张图像 x 生成两个随机增强视图 v 和 v'。

   • Step 2: 将视图 v 输入在线网络，得到输出 y_θ = g_θ(f_θ(v))，再通过预测头得到最终预测 q_θ(y_θ)。

   • Step 3: 将视图 v' 输入目标网络，得到输出 y'_ξ = g_ξ(f_ξ(v'))。注意，目标网络提供的是一个稳定的“回归目标”。（表征+投影的思想 借鉴SimCLR）

   • Step 4: 计算损失函数：在线网络的预测 q 与目标网络的输出 y 的均方误差（MSE），并对 v 和 v' 交换角色再计算一次损失。

   • Step 5: 最小化总损失 L，只更新在线网络（θ）的参数。

   • Step 6: 使用动量更新规则来更新目标网络（ξ）的参数：ξ ← τξ + (1-τ)θ 。（借鉴MoCo）

为什么只用正样本 不会产生坍塌collapse？

神奇博客 用MOCOv2（MLP中不含BN）复现BYOL 发现坍塌了 怀疑BN和不坍塌有强烈关系。

博客解释：整个batch算来的均值和方差去做归一化，在算某个样本的loss的时候，其实也看到了其他样本的特征，这里面是有泄露的，所以你可以把batch里的其他样本想成一种隐式的负样本。

换句话说，当你有了bn的时候，BYOL其实并不是只是正样本在自己和自己学，其实也在做对比，BYOL做的对比任务就是：当前正样本的图片，和BN产生的平均图片的差别。

BYOL works even without batch statistics

论文作者作出回应 利用消融实验。 比较小的结果代表坍塌了。

右下角 SimCLR 编码和投影不用归一化的话；也炸了。人家是有显式负样本的。

有一组 Projector 有BN也失败了。 

这两个例子 说明BN和隐式负样本无关。

结论：BN的主要作用只是帮助模型稳定训练，提高模型训练的稳健性，让模型不会坍塌。

3.2 SimSiam 简化的 总结性的工作

Exploring Simple Siamese Representation Learning

even using none of the following: (i) negative sample pairs, (ii) large batches, (iii) momentum encoders. 负样本；大批量；动量更新自编码器 这些都不需要。

两个网络共享参数

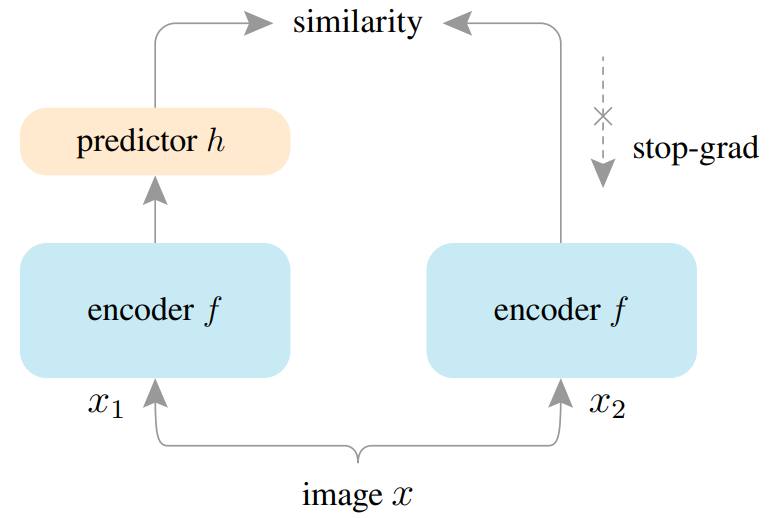
stop-grad 防止坍塌的核心；否则x1接近x2 x2接近x1 参数更新时会坍塌。

在计算 余弦相似度损失函数时 用z.detach() 阻断梯度回传，避免对称性的双向更新。

一个分支（带有预测头 h）的任务是去预测另一个分支（目标分支）的输出，而目标分支是相对稳定的（防止互相抄袭）。

• 在计算 D(p1, z2) 时，f 通过 z1（来自 x1）的梯度进行更新。

• 在计算 D(p2, z1) 时，f 通过 z2（来自 x2）的梯度进行更新。

# f: backbone + projection mlp
# h: prediction mlpfor x in loader: # load a minibatch x with n samplesx1, x2 = aug(x), aug(x) # random augmentationz1, z2 = f(x1), f(x2) # projections, n-by-dp1, p2 = h(z1), h(z2) # predictions, n-by-dL = D(p1, z2)/2 + D(p2, z1)/2 # lossL.backward() # back-propagateupdate(f, h) # SGD updatedef D(p, z): # negative cosine similarity 余弦相似度z = z.detach() # stop gradientp = normalize(p, dim=1) # l2-normalizez = normalize(z, dim=1) # l2-normalizereturn -(p*z).sum(dim=1).mean()

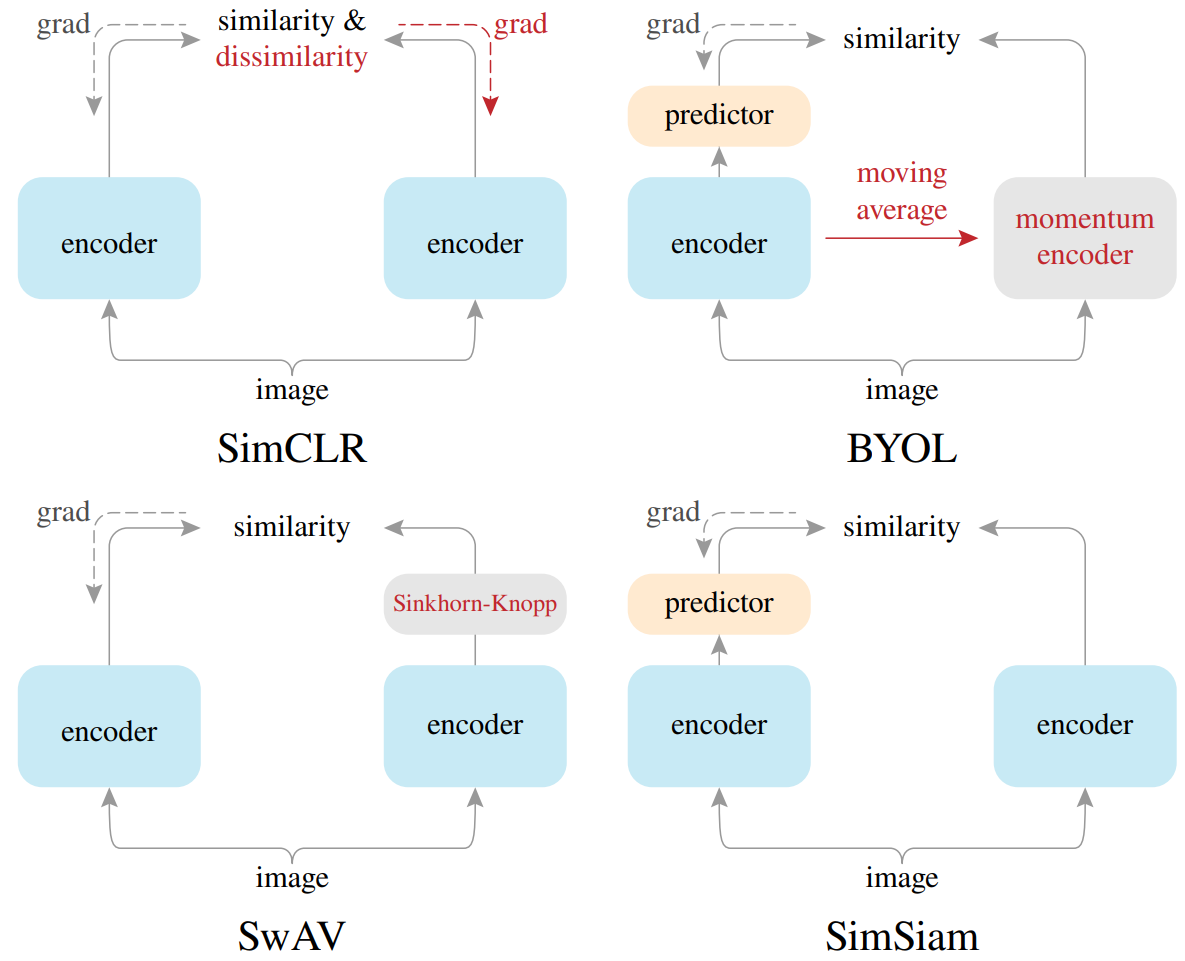
四个架构的对比：

SimCLR 端到端 两把都需要grad ； SwAV 用SK算法得到聚类中心；

BYOL 有一个predictor 转换为预测任务；SimSiam 没用动量编码器而是共享参数。

在原分类问题上 （SwAV不用multi-crop的话）最强的分类模型是BYOL

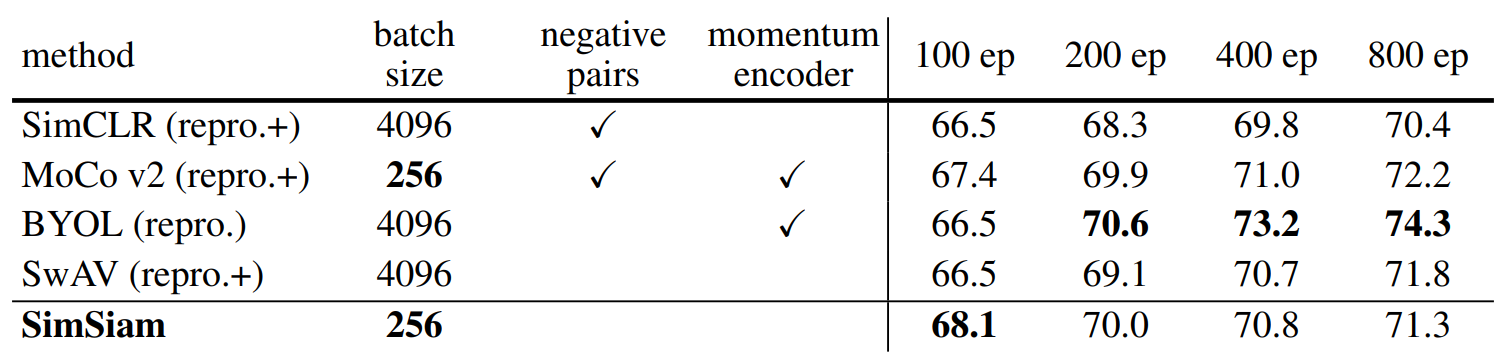
下游任务迁移学习上 MoCo和SimSiam在 VOC和COCO 目标检测上表现更好

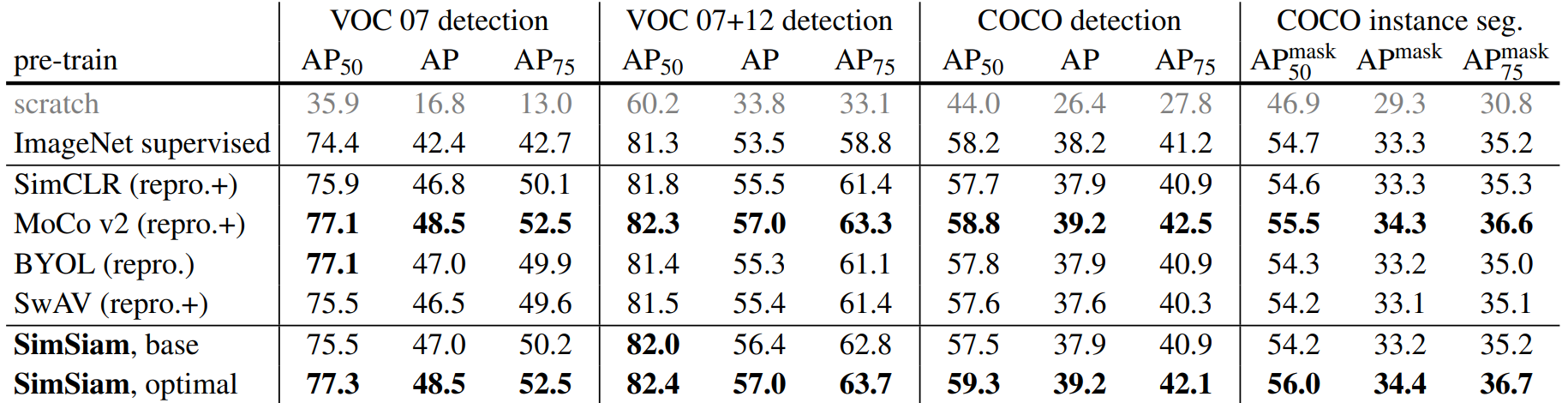
还有一种算法 Barlow Twins 损失函数直接作用在交叉相关矩阵 C 上，其目标是让这个矩阵尽可能接近单位矩阵。

第四阶段：融合Transformer （ViT出来之后）

4.1 MoCo-v3

An Empirical Study of Training Self-Supervised Vision Transformers

架构上 结合了MoCo-v2和SimSiam。

学习MoCo-v2：q和momentum_k 两个网络 + 对比学习loss

学习SimSiam：predictor + 对称损失

# f_q: encoder: backbone + proj mlp + pred mlp
# f_k: momentum encoder: backbone + proj mlp
# m: momentum coefficient
# tau: temperature
for x in loader: # load a minibatch x with N samplesx1, x2 = aug(x), aug(x) # augmentationq1, q2 = f_q(x1), f_q(x2) # queries: [N, C] eachk1, k2 = f_k(x1), f_k(x2) # keys: [N, C] eachloss = ctr(q1, k2) + ctr(q2, k1) # symmetrizedloss.backward()update(f_q) # optimizer update: f_qf_k = m*f_k + (1-m)*f_q # momentum update: f_k# contrastive loss
def ctr(q, k):logits = mm(q, k.t()) # [N, N] pairslabels = range(N) # positives are in diagonalloss = CrossEntropyLoss(logits/tau, labels)return 2 * tau * loss

骨干网络backbone 从残差网络换成了 Transformer。

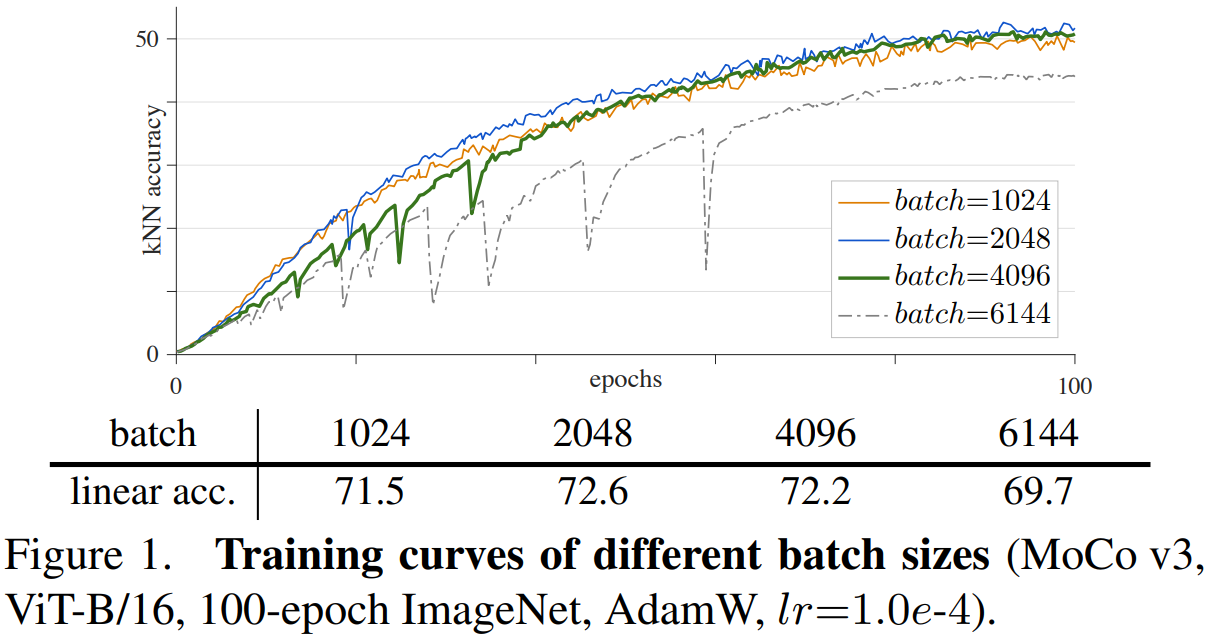
训练稳定性问题stability 大batch=6144 训练一段准确率会掉下去。

查梯度发现 在第一次patch分割的时候 有梯度波峰。

Trick：随机初始化再冻住 a fixed random patch projection layer

4.2 DINO 自蒸馏 Self-distillation with no labels

Emerging Properties in Self-Supervised Vision Transformers

开头效果比较炸裂的图 ViT 无监督情况下，自注意力图片 自动实现分割轮廓。

就像BYOL的在线和目标 叫做学生和老师；老师网络centering中心化（类似BN）防止坍塌。

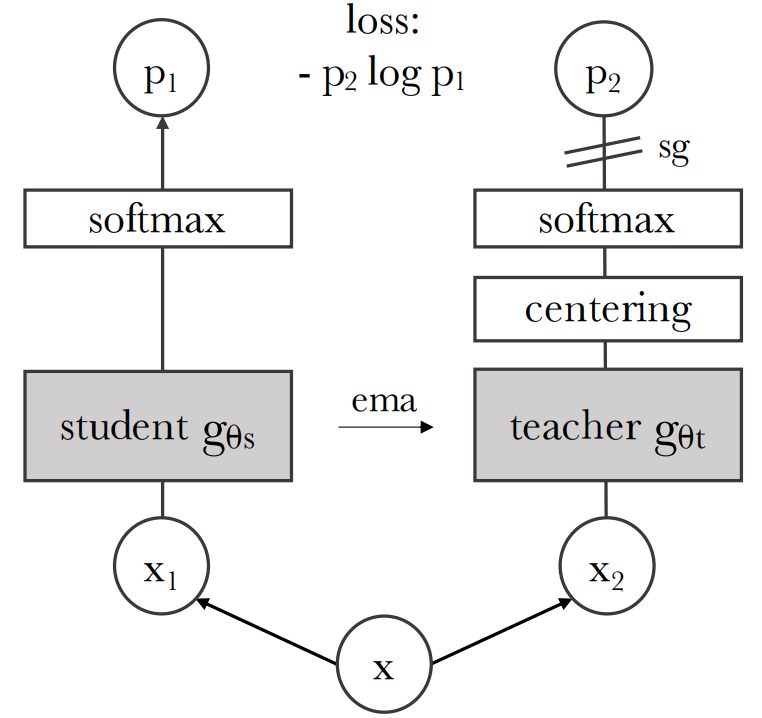
# gs, gt: student and teacher networks
# C: center (K)
# tps, tpt: student and teacher temperatures
# l, m: network and center momentum rates
gt.params = gs.params
for x in loader: # load a minibatch x with n samplesx1, x2 = augment(x), augment(x) # random viewss1, s2 = gs(x1), gs(x2) # student output n-by-Kt1, t2 = gt(x1), gt(x2) # teacher output n-by-Kloss = H(t1, s2)/2 + H(t2, s1)/2loss.backward() # back-propagate# student, teacher and center updatesupdate(gs) # SGDgt.params = l*gt.params + (1-l)*gs.paramsC = m*C + (1-m)*cat([t1, t2]).mean(dim=0)def H(t, s):t = t.detach() # stop gradients = softmax(s / tps, dim=1)t = softmax((t - C) / tpt, dim=1) # center + sharpenreturn - (t * log(s)).sum(dim=1).mean()