一阶低通滤波在运动控制中的应用
1. 核心思想:为什么要用低通滤波?
在机器人运动控制中,未经滤波的信号主要存在两个问题:
- 高频噪声:来自关节电机的电流环、编码器测量量化误差、IMU的微小振动等。
- 指令突变:上层规划器发出的指令(如期望运动速度、身体高度)可能是阶跃变化的。
低通滤波的作用就是在平滑噪声/减缓冲击和快速响应指令之间做一个权衡。这个权衡的“旋钮”就是滤波器的截止频率。
2. 连续时域理念
2.1 数学模型:微分方程
我们希望设计一个系统,其输出 y(t)y(t)y(t) 的变化率(导数)不仅取决于当前输入 x(t)x(t)x(t),还受到当前输出值的“牵制”。这种关系引向了一个一阶微分方程,它描述了一个具有“惯性”或“记忆”的系统:
τdy(t)dt+y(t)=x(t) \tau \frac{dy(t)}{dt} + y(t) = x(t) τdtdy(t)+y(t)=x(t)
推导与证明:方程的物理意义
方程可以改写为:
dydt=1τ(x−y) \frac{dy}{dt} = \frac{1}{\tau}(x - y) dtdy=τ1(x−y)
这个形式表明:
- 系统输出 y(t)y(t)y(t) 的变化率 dydt\frac{dy}{dt}dtdy 与当前误差 (x−y)(x - y)(x−y) 成正比。
- 时间常数 τ\tauτ 是比例系数。τ\tauτ 越大,同样的误差引起的输出变化越慢,系统惯性越大。
- 系统总是“试图”让输出 yyy 跟上输入 xxx,但这个追赶过程受到 τ\tauτ 的制约。
其中:
- x(t)x(t)x(t):输入信号(原始的、带噪声的测量值或突变的指令)
- y(t)y(t)y(t):输出信号(过滤后的平滑信号)
- τ\tauτ:时间常数(关键参数,决定“惯性”大小)
2.2 关键参数:时间常数 τ\tauτ 与截止频率 fcf_cfc
-
时间常数 τ\tauτ:
- τ\tauτ 越大:系统惯性越大,响应越“迟钝”,更平滑,延迟越大。
- τ\tauτ 越小:系统惯性越小,响应越快,平滑效果差。
-
截止频率 fcf_cfc:
fc=12πτ f_c = \frac{1}{2\pi\tau} fc=2πτ1
推导与证明:截止频率的由来
为了分析系统对不同频率信号的响应,我们使用拉普拉斯变换,将微分方程转换为代数方程。对原方程两边进行拉普拉斯变换(假设零初始条件):
L{ τdydt+y}=L{ x}τsY(s)+Y(s)=X(s)(τs+1)Y(s)=X(s) \mathcal{L}\{\tau \frac{dy}{dt} + y\} = \mathcal{L}\{x\} \\ \tau s Y(s) + Y(s) = X(s) \\ (\tau s + 1)Y(s) = X(s) L{ τdtdy+y}=L{ x}τsY(s)+Y(s)=X(s)(τs+1)Y(s)=X(s)
得到传递函数:
H(s)=Y(s)X(s)=1τs+1 H(s) = \frac{Y(s)}{X(s)} = \frac{1}{\tau s + 1} H(s)=X(s)Y(s)=τs+11
令 s=jωs = j\omegas=jω (jjj是虚数单位,ω\omegaω是角频率),得到频率响应:
H(jω)=1jωτ+1 H(j\omega) = \frac{1}{j\omega \tau + 1} H(jω)=jωτ+11
其幅度(增益)为:
∣H(jω)∣=1(ωτ)2+1 |H(j\omega)| = \frac{1}{\sqrt{(\omega \tau)^2 + 1}} ∣H(jω)∣=(ωτ)2+11
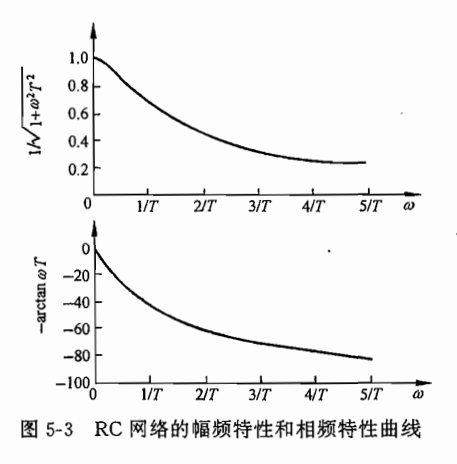
当增益下降到直流(ω=0\omega=0ω=0)增益的 1/21/\sqrt{2}1/2(即-3dB)时,对应的频率即为截止频率:
1(ωcτ)2+1=12(ωcτ)2+1=2ωc=1τ \frac{1}{\sqrt{(\omega_c \tau)^2 + 1}} = \frac{1}{\sqrt{2}} \\ (\omega_c \tau)^2 + 1 = 2 \\ \omega_c = \frac{1}{\tau} (ωcτ)2+11=21(ωcτ)2+1=2ωc=τ1
由于 ω=2πf\omega = 2\pi fω=2πf,所以:
fc=ωc2π=12πτ f_c = \frac{\omega_c}{2\pi} = \frac{1}{2\pi\tau} fc=2πωc=2πτ1- 如何选 fcf_cfc?
- 过滤噪声:将 fcf_cfc 设在噪声频率以下。(例如:滤除50Hz以上噪声,设 fcf_cfc = 30Hz)
- 平滑指令:fcf_cfc 必须远低于机器人的结构谐振频率和电机带宽。(通常从10-20Hz开始调试)
- 如何选 fcf_cfc?
2.3 阶跃响应:直观理解动态性能
对一个理想的阶跃输入 x(t)=u(t)x(t)
