Self-supervised Feature Adaptation for 3D Industrial Anomaly Detection 论文精读

题目：Self-supervised Feature Adaptation for 3D Industrial Anomaly Detection

题目：用于 3D 工业异常检测的自监督特征自适应

论文地址：ECCV 2024 2401
Self-supervised 自监督
Feature Adaptation 特征自适应
for 用于
3D Industrial Anomaly Detection 3D 工业异常检测

Abstract 摘要

  工业异常检测通常作为一项无监督任务来开展，旨在仅利用正常训练样本定位缺陷。近年来，大量2D异常检测方法被提出并取得了不错的成果；然而，仅以2D RGB数据作为输入，不足以识别难以察觉的几何表面异常。因此，本文聚焦于多模态异常检测。
  具体而言，我们研究了早期的多模态方法——这类方法试图利用在大规模视觉数据集（如ImageNet）上预训练的模型来构建特征库；但经验表明，直接使用这些预训练模型并非最优选择，它们要么无法检测出细微缺陷，要么会将异常特征误判为正常特征。这可能是由于目标工业数据与源数据之间存在领域差异。
  为解决该问题，我们提出了一种 局部到全局的自监督特征适配（LSFA） 方法，用于微调适配器并学习面向异常检测任务的表示。在LSFA中，模态内适配和跨模态对齐均从“局部到全局”的视角进行优化，以保证推理阶段的表示质量与一致性。
  大量实验表明，我们的方法不仅能显著提升基于特征嵌入的方法的性能，还在MVTec-3D AD和Eyecandies数据集上均大幅超越了以往的最先进（SoTA）方法；例如，LSFA在MVTec-3D上实现了97.1%的图像级ROC曲线下面积（I-AUROC），较以往SoTA提升了3.4%。

1. Introduction 引言

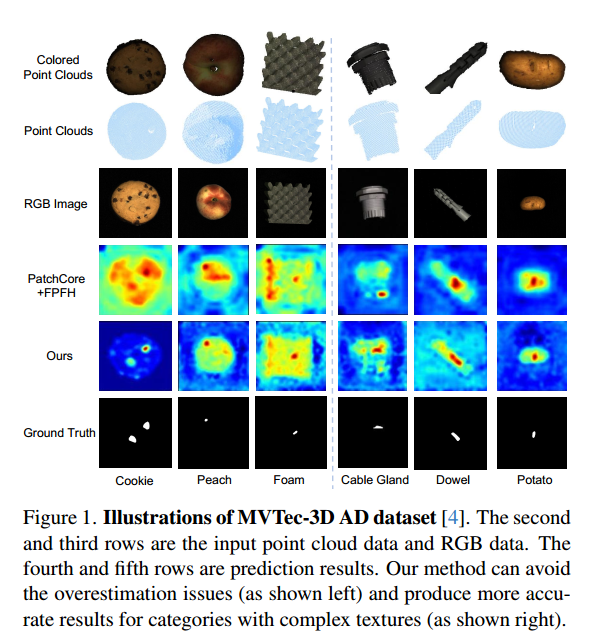
  工业异常检测是一个广泛探索的计算机视觉任务，旨在检测工业产品中图像级/像素级的异常模式 [22]。由于现实场景中异常样本匮乏，当前异常检测方法通常遵循无监督范式 [2, 10, 15, 18, 21, 25, 26, 30–34]——即仅用正常样本训练模型，再在正常与异常样本混合的场景下测试。以往的大多数方法 [10, 30, 35] 为 2D 图像设计，且在 2D 异常检测中取得了巨大成功。然而，在工业检测场景中，由于缺乏深度信息，仅靠 RGB 信息有时难以区分细微的表面缺陷与正常纹理（例如图 1 中的饼干）。因此，近期出现的新基准 [4, 6] 鼓励从多模态视角开展异常检测研究，其中物体通过 2D 图像和 3D 点云共同表示。
  为实现精准的异常定位，现有 2D 异常检测方法大致分为两类：基于重建的方法和基于特征嵌入的方法。前者利用仅用正常特征训练的生成器无法成功重建异常特征的特点；后者则通过训练良好的特征提取器建模正常样本的分布，推理阶段将“分布外样本”视为异常。
  基于特征嵌入的方法更灵活，在 2D RGB 异常检测任务中表现出良好性能。但将 2D 异常特征嵌入范式简单迁移到 3D 领域并不容易。以最先进的基于嵌入的方法 PatchCore [26] 为例：当它与手工设计的 3D 表示（FPFH [17]）结合时，能形成强大的多模态异常检测基线；但如图 1 所示，我们通过实验发现 PatchCore+FPFH 基线存在两个缺陷：

• 首先，由于预训练知识与工业场景差异较大（见图 1 左侧），它容易将异常区域误判为正常区域；
• 其次，对于纹理更复杂的类别，它有时无法识别小的异常模式（如图 1 右侧所示）。

  为解决上述问题，我们采用特征适配策略来增强预训练模型的能力，并学习面向任务的特征描述子：

• 在模态层面：颜色更有助于识别纹理异常，深度信息有助于检测 3D 空间的几何变形 [17]，因此利用模态内和跨模态信息进行适配更合理；
• 在粒度层面：模态间的“对象级对应”有助于学习紧凑表示，而异常检测需要“局部敏感性”来识别细微异常 [26]，因此多粒度学习目标十分必要。

  基于上述考虑，我们提出了一种新颖的局部到全局自监督多模态特征适配框架（Local-to-global Self-supervised multi-modal Feature Adaptation，LSFA），以更好地将预训练知识迁移到下游异常检测任务中。具体而言，LSFA 从两个视角进行适配：

• 模态内适配：引入**模态内特征紧致性（Intra-modal Feature Compactness, IFC）**优化，通过多粒度记忆库学习正常特征的紧凑分布；
• 跨模态适配：设计跨模态局部到全局一致性（Cross-modal Local-to-global Consistency, CLC），在 patch 级和对象级对齐不同模态的特征。

  借助多模态的多粒度信息，经 LSFA 适配的模型会生成“面向 3D 空间异常检测”的目标导向特征——既能捕捉小异常，又能避免误报（如图 1 所示）。在异常检测的最终推理中，我们利用 LSFA 微调后的特征构建记忆库，并通过计算特征差异判断“正常/异常”（如 [26] 所述）。

  LSFA 的有效性在主流基准（包括 MVTec-3D 和 Eyecandies）上得到验证：在 MVTec-3D 上，LSFA 以较大优势超越了以往的最先进方法（SoTA）[28]，实现了 97.1%（+3.4%）的 I-AUROC。

  本文的主要贡献如下：

• 提出 LSFA：这是一个面向 3D 异常检测的新颖且有效的框架，以“模态间的局部到全局对应”为监督来适配预训练特征。该方法在主流基准上表现出显著优势，并创造了新的 SoTA。
• 提出 模态内特征紧致性优化（IFC）：通过动态更新的记忆库，从“patch 层面”和“原型层面”提升特征紧致性。
• 提出 跨模态局部到全局一致性对齐（CLC）：利用多粒度对比信号缓解跨模态错位问题。

2. Related Work 相关工作

  由于我们的工作主要涉及计算机视觉的两个方面，即2D/3D工业异常检测，因此在本节中，我们分别简要介绍以往的传统2D/3D工业异常检测方法。

2.1 2D industrial anomaly detection 2D工业异常检测

  作为一项二分类任务，无监督工业异常检测仅使用正常样本训练模型，以区分从“正常/异常分布”中采样的实例并定位异常区域，这引起了广泛关注 [22]。现有方法主要分为两类：基于重建的方法和基于特征嵌入的方法。在以往基于重建的方法中，基于知识蒸馏的方法 [3, 10, 29] 假设“预训练的教师模型”与“学生模型”在异常块的表示上存在差异——训练过程中，学生模型被训练为模拟教师模型对正常样本的输出。为了防止“教师与学生使用相同滤波器”带来的负面影响，[10] 整合了一种反向流范式，这也能阻止异常梯度传播到学生模型。[1, 14] 开展隐式特征建模，并基于“异常块无法被很好恢复”的假设，通过比较重建图像与输入图像来检测缺陷。

  除这些方法外，基于特征嵌入的方法近期通过利用“在大规模外部自然图像数据集（即 ImageNet）上预训练的模型”所提取的特征，取得了最先进的性能，且无需进一步适配目标领域的数据。基于 Normalizing flow [16, 35] 的方法通过可逆地将正常特征转换为正态分布来区分缺陷；PaDiM [9] 考虑不同语义层之间的相关性，以提取局部受约束的表示并估计块级特征分布的矩；PatchCore [26] 将正常块级特征存储在记忆库中，通过比较“目标特征”与“正常特征”来定位缺陷；CFA [20] 提出一种耦合超球面微调框架，以将块特征适配到目标数据集，从而减轻对异常特征“正常性”的过高估计。

2.2 3D industrial anomaly detection 3D 工业异常检测

  与 2D 工业异常检测不同，3D 工业异常检测通过同时考虑 RGB（图像）和点云样本，来识别异常块。[4] 提出了首个公开的 3D 异常检测基准——MVTec-3D AD，用于方法评估，并基于体素自动编码器和生成对抗网络构建了基线方法：通过比较“输入体素”与“重建体素”之间的体素级差异来定位异常缺陷。然而，由于 [4] 缺乏对多模态数据中空间结构信息的整合，只能获得微小的精度提升。受此启发，[5] 提出了一种 3D 师生框架，以提取点云的“局部几何感知描述子”，并利用额外辅助数据进行鲁棒预训练。[17] 首次探索了“记忆库”在该任务中的应用，并利用从预训练模型中提取的局部几何特征。但由于 [17] 未对“有偏差的特征”在目标领域进一步适配，其与最先进方法之间存在显著的性能差距。为解决这一问题，M3DM [31] 提出了一种多模态工业异常检测方法，通过混合特征融合来促进多模态特征间的交互。
  然而，这些方法在执行跨模态对齐时，普遍忽视了模态内特征紧致性的重要性。因此，它们提取的单模态特征可能形成“异常/正常特征难以相互区分”的分布。这种特征分布也限制了它们有效整合两种模态信息的能力，进而导致异常检测不准确。此外，这些方法仅考虑局部级的跨模态对齐，而未纳入特征的全局级对齐——后者对于增强两种模态间的信息交互也至关重要。受此启发，我们提出一种“局部到全局的自监督多模态适配方法”，从块级和对象级两个视角，提升基于特征嵌入的方法的异常检测性能。

3. Methodology 方法

3.1. Overview 概述

3.1.1 Framework overview and symbol definition 框架概述与符号定义

  在本节中，我们首先给出我们的LSFA框架的概述。

两种模态输入：点云+RGB
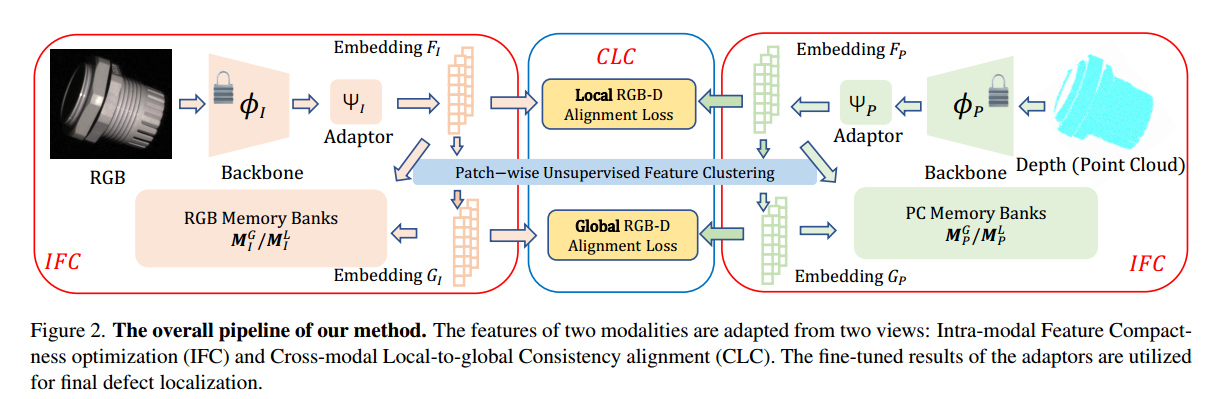
  如图2所示，LSFA将集合$\mathbb{D}=\{(P_i,I_i){\}}_{i=1}^{|\mathbb{D}|}$中的点云与RGB图像均作为输入，以开展联合缺陷检测，其中$P_i\in {\mathbb{R}}^{N\times 3}$（$P_i$为点云，维度是$N$个点、每个点3维坐标），$I_i\in {\mathbb{R}}^{H\times W\times 3}$（$I_i$为RGB图像，维度是高度$H$、宽度$W$、3个颜色通道）。
预训练的特征提取器+一个基础的Transformer编码器层作为这些特征的适配器
  对于两种模态的表示$P_i$（点云模态）和$I_i$（RGB图像模态），我们采用预训练的特征提取器${\varphi }_P/{\varphi }_I$来获取特定于模态的表示。由于预训练骨干网络与下游检测任务之间存在严重的领域偏差，我们使用一个基础的Transformer编码器层[12]作为这些特征的适配器（需注意，我们在附录中还探究了几种其他的适配器结构）。
面向任务的特征自适应：IFC+CLC
  RGB/3D模态的适配器分别记为${\Psi }_I(\cdot )$（RGB模态适配器）和${\Psi }_P(\cdot )$（3D模态适配器）。我们提出从两个视角对${\Psi }_I(\cdot )/{\Psi }_P(\cdot )$执行面向任务的特征自适应：模态内特征紧致性优化（IFC）与跨模态局部-全局一致性对齐（CLC）。
  (1) IFC为RGB和3D模态均构建了全局级和局部级的动态更新记忆库，以从多粒度视角最小化“正常特征”之间的距离，进而更好地区分正常特征与异常特征。
  (2) CLC由“局部到全局的跨模态对齐模块”组成，这些模块可缓解两种模态之间的特征错位，并借助自监督信号增强空间结构的多模态信息交互。

3.1.2 Inference with adapted representation 基于自适应表示的推理

  在自适应过程之后，由于对局部敏感的特征更有助于检测异常模式，全局特征在最终推理阶段会被舍弃。对于RGB或点云的任一模态，仅使用来自适配器的局部特征，通过现成的PatchCore算法[26]来计算每个像素/体素的异常分数。最后，将两种模态的异常分数取平均，作为最终的异常估计结果。

3.2. CLC: Cross-modal Local-to-global Consistency Alignment CLC：跨模态局部-全局一致性对齐

3.2.1 Feature projection 特征投影

3.2.1.1 VIT提取图像块特征+PointMAE提取组级特征

  为提取对异常检测敏感的局部特征，Vision Transformer（ViT）[12] 和 PointMAE [24] 被用作 ${\varphi }_I$/${\varphi }_P$。ViT 将 2D 图像 $I_i$ 分割为 $N_m$ 个 patch，并为每个 patch 提取深度特征；相应地，PointMAE 将 $P_i$ 中的 3D 点划分为 $N_d$ 个组，并提取组级特征。
  为在两种模态间建立密集的局部对应关系，我们通过几何插值与投影，将 3D 点重新映射到 2D patch 中。

3.2.1.2 三维点云的组级特征映射到逐点的深度特征

  具体而言，我们将第 $i$ 个点组的深度特征记为 $A_i$，组中心记为 $c_i\in {\mathbb{R}}^3$；随后，对于 $P_i$ 中的每个点 $p\in {\mathbb{R}}^3$，可通过基于距离的插值得到逐点深度特征 $f_p$：
$$f_p=\sum _{i=1}^{N_d}{\alpha }_i{A}_i,{\alpha }_i=\frac{\frac{1}{\Vert c_i-p{\Vert }_2}}{{\sum }_{k=1}^{N_m}\frac{1}{\Vert c_k-p{\Vert }_2}}.(1)$$

  从上下文逻辑来看，这里的$N_m$很可能是笔误，应该为$N_d$。
  原因如下：
   PointMAE将3D点划分为$N_d$个组，每个组的中心是$c_i\in {\mathbb{R}}^3$（共$N_d$个组中心）。计算点$p$的逐点深度特征$f_p$时，插值权重${\alpha }_i$的分母是“所有组中心与$p$距离的倒数之和”，因此求和范围应该是3D点分组的数量$N_d$，而非ViT中图像patch的数量$N_m$。
  修正后，分母应为${\sum }_{k=1}^{N_d}\frac{1}{\Vert c_k-p{\Vert }_2}$，这样才能保证对3D点的$N_d$个组进行权重归一化。

3.2.1.3 逐点特征映射到二维空间中，得到3D点特征的2D逐 patch表示

  同时，我们可借助相机参数验证 3D 点 $p$ 是否被投影至 2D patch 中；因此，对于来自 ViT 的每个图像 patch，我们对所有投影到同一patch内的点的特征 $f_p$取平均，将其作为原始点云特征的 2D 投影。
  通过这种方式，我们得到3D点特征的2D逐 patch表示——它与图像特征具有相同的 patch 数量 $N_m$；并且，通过关联同一 patch 的 RGB 特征与投影后的点特征，可自然获得局部对应关系。
一个块既有2D特征又有3D特征

3.2.1.3 RGB和点云的逐patch 分别输入各自的适配器中，产生自适应特征

  最后，RGB 和点云的逐 patch 表示分别被输入至适配器=${\Psi }_I(\cdot )$/${\Psi }_P(\cdot )$ 中。经自适应后的特征记为 ${\mathbb{D}}_F=\{(F_{P_i},F_{I_i}){\}}_{i=1}^{|\mathbb{D}|}$。

  $\{(F_{P_i},F_{I_i}){\}}_{i=1}^{|\mathbb{D}|}$ 中的 $|\mathbb{D}|$不是单张图像的 patch 数 $N_m$，而是输入数据的总样本数（即有多少组“点云 $P_i$ + 图像 $I_i$”的样本对）。

• $N_m$：是单张 RGB 图像被 ViT 分割后得到的 patch 数量（属于“单样本内的局部单元数量”）。
• $|\mathbb{D}|$：是输入数据集 $\mathbb{D}=\{(P_i,I_i){\}}_{i=1}^{|\mathbb{D}|}$ 中，样本对的总数量（即有多少个这样的“点云-图像”对参与处理）。

3.2.2 Cross-modal local-to-global consistency alignment 跨模态局部-全局一致性对齐

  经过上一步后，两种模态的特征在空间位置上实现了对齐。然而，若自适应过程中缺乏跨模态交互，在推理阶段融合两种模态的异常分数时，跨模态特征错位可能导致效果不佳。
  为解决这一问题，如图3所示，我们执行局部-全局一致性对齐——该操作可利用跨模态自监督信号来提升特征质量。

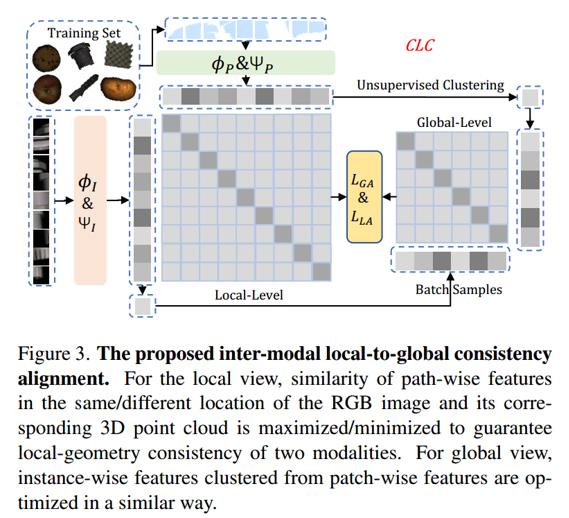
  具体而言，针对RGB/3D点云的适配逐patch特征{FIi,FPi}i=1Nb\{F_{I_i}, F_{P_i}\}_{i=1}^{N_b}{FIi​​,FPi​​}i=1Nb​​，首先通过两个全连接层映射到相同维度，记为$H_I/H_P$（其中 $N_b$为批量大小）。投影后的特征记为{FIi′,FPi′}i=1Nb\{F'_{I_i}, F'_{P_i}\}_{i=1}^{N_b}{FIi​′​,FPi​′​}i=1Nb​​，随后计算逐patch的对比损失，以最大化不同模态但相同位置的patch之间的特征相似性，并最小化不同位置的patch之间的相似性：
$${\mathcal{L}}_{LA}=-\log \left(\frac{\exp \left(⟨F_{I_i}^{\prime j},F_{P_i}^{\prime j}⟩\right)}{{\sum }_{t=1}^{N_m}{\sum }_{k=1}^{N_m}\exp \left(⟨F_{I_i}^{\prime t},F_{P_i}^{\prime k}⟩\right)}\right),(2)$$
  其中$⟨\cdot ,\cdot ⟩$表示向量间的内积。由于公式2仅涉及局部几何线索，却缺少全局结构信息的交互，我们通过k均值聚类算法对局部特征$F_{I_i}$/$F_{P_i}$进一步聚类，得到逐实例特征$G_{I_i}$/$G_{P_i}$。随后，对这些全局特征执行类似操作，相应的全局对齐损失记为${\mathcal{L}}_{GA}$：
$${\mathcal{L}}_{GA}=-\log \left(\frac{\exp \left(⟨G_{I_i}^{\prime },G_{P_i}^{\prime }⟩\right)}{{\sum }_{t=1}^{N_b}{\sum }_{u=1}^{N_b}\exp \left(⟨G_{I_t}^{\prime },G_{P_u}^{\prime }⟩\right)}\right).(3)$$
  因此，CLC的整体损失函数可表示为：
$${\mathcal{L}}_{CLC}={\mathcal{L}}_{LA}+{\mathcal{L}}_{GA}.(4)$$

3.3. IFC: Intra-modal Feature Compactness Optimization 模态内特征紧致性优化

  所提出的模态内特征紧致性优化策略，旨在帮助模型为正常样本生成更紧凑的表示，进而使模态对异常模式更敏感。

3.3.1 Local-to-global compactness optimization 局部到全局的紧致性优化

  由于未经自适应的预训练模型存在严重的领域偏差，提取的特征可能形成“异常与正常特征难以相互区分”的分布。因此，以往基于特征嵌入的方法[17]不可避免地容易将异常误判为正常区域。

  基于特征嵌入的方法核心逻辑是将数据映射到低维特征空间，通过特征间的相似度判断是否为异常”，具体流程可拆解为三步，结合“领域偏差”的缺陷理解如下：
  
一、步骤1：特征提取（用预训练模型提特征）
   首先利用预训练深度学习模型（如CNN、Transformer）提取数据的特征。

• 正常流程：模型在“源领域”（如大规模通用数据集）预训练后，直接用来提取“目标领域”（如工业场景的图像/点云）的特征。
• 问题：若目标领域与源领域差异大（即“领域偏差”），提取的特征会扭曲——异常和正常特征的分布重叠严重，导致后续无法区分。

二、步骤2：嵌入空间构建（把特征映射到统一空间）
  将提取的特征映射到一个低维“嵌入空间”（可理解为更简洁的特征空间），让正常样本的特征在空间中聚集，异常样本的特征偏离这个聚集区。常见方法有3种：
  （1）师生架构（Teacher-Student Architecture）
    - 逻辑：用“教师模型”（预训练的固定网络）和“学生模型”（可训练的轻量网络）协同学习。教师模型教学生模型“正常特征的分布”，让学生模型提取的正常特征与教师模型一致，而异常特征因偏离正常分布，会与教师模型的特征差异显著。
    - 缺陷：若教师模型因领域偏差本身提取的特征分布扭曲，学生模型学到的“正常分布”也是错的，容易把异常误判为正常。
   （2）单类分类（One-Class Classification）
    - 逻辑：把问题转化为“只区分正常样本”的单分类任务。在嵌入空间中学习一个“特征边界”，把正常样本围在边界内，异常样本因超出边界被检测。
    - 缺陷：依赖“正常样本的特征分布足够紧凑”，若领域偏差导致正常样本特征本身分散，边界无法准确划分，异常易漏判。
  （3）记忆库（Memory Bank）
    - 逻辑：先把所有正常样本的特征存储在“记忆库”中（相当于构建“正常特征字典”）；测试时，计算待检测样本的特征与记忆库中正常特征的**距离**——距离越远，越可能是异常。
    - 缺陷：若记忆库中的正常特征因领域偏差“本身就包含异常模式”（比如预训练时混入了异常样本的特征），则异常检测会失效。
三、步骤3：异常判定（通过特征相似度/距离判断）
  在嵌入空间中，用距离度量（如欧氏距离、余弦相似度）判断待检测样本是否为异常：

• 若待检测样本的特征与“正常特征聚集区”的距离超过阈值→判定为异常；
• 若距离在阈值内→判定为正常。

四、为何会“将异常误判为正常”？（领域偏差的影响）
  如原文所述，“未经自适应预训练的模型存在领域偏差”，导致异常和正常特征的分布重叠：

• 异常特征可能因领域偏差，被模型错误地映射到“正常特征聚集区”附近；
• 正常特征也可能因领域偏差，被映射到“异常区”。 此时，特征嵌入方法无法有效区分两者，自然会把异常误判为正常。

五、举个直观例子（工业图像异常检测）
  假设用预训练CNN提取“正常齿轮图像”和“有裂纹的异常齿轮图像”的特征：

• 若模型无领域自适应，可能把“裂纹”的特征错误地映射到“正常齿轮特征区”（因为预训练数据里没有齿轮，领域偏差导致特征提取失真）；
• 此时用“记忆库”或“师生架构”检测，会认为“裂纹齿轮”的特征与正常特征距离近→误判为正常。

   简言之，基于特征嵌入的方法是用预训练模型提特征→映射到嵌入空间→靠距离/相似度判异常；但领域偏差导致特征分布扭曲是核心痛点，也是后续“动态更新记忆库”等改进方法的动机。

  受此启发，如图4所示，我们设计了一个在局部和全局层面动态更新的记忆库，以指导紧致性优化。

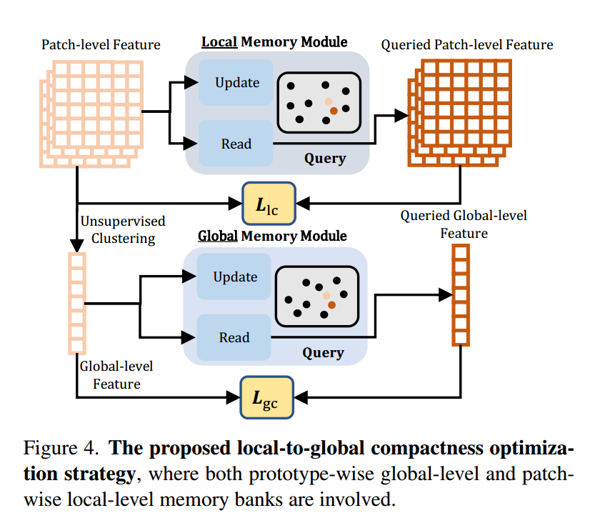
  由于优化是在每个模态内部进行的，此处我们以RGB特征为例，点云特征的处理方式与之类似。具体来说，我们将由patch级RGB特征组成的记忆库记为$M_I^L$，其长度为$|M_I^L|=n_I^L$。批量{FIi}i=1Nb\{F_{I_i}\}_{i=1}^{N_b}{FIi​​}i=1Nb​​中图像$I_i$的第$j$个patch级特征$F_{I_i}^j$，会被用于在$M_I^L$中进行最近邻搜索（其中$N_b$)为批量大小）。我们采用均方误差损失来最小化$F_{I_i}^j$与其在$M_I^L$中对应最近邻项之间的差异。因此，局部patch级紧致性损失${\mathcal{L}}_{\text{LC}}$可推导为：
$${\mathcal{L}}_{\text{LC}}=\sum _{i=1}^{N_b}\sum _{j=1}^{N_m}\underset{Q\in M_I^L}{\min }{\Vert F_{I_i}^j-Q\Vert }_2.\text{\hspace{1em}(5)}$$
  其中$N_m$为patch的数量。
  此外，为增强每类特征的紧致性，我们设计了全局紧致性损失，以同时优化全局特征$G_{I_i}$。将由长度为$n_I^G$的全局RGB特征组成的记忆库记为$M_I^G$。对$G_{I_i}$和$M_I^G$执行类似的最近邻搜索操作，以从全局视角增强对异常的敏感性。因此，全局紧致性损失${\mathcal{L}}_{\text{GC}}$为：
$${\mathcal{L}}_{\text{GC}}=\sum _{i=1}^{N_b}\underset{Q\in M_I^G}{\min }{\Vert G_{I_i}^j-Q\Vert }_2.\text{\hspace{1em}(6)}$$
  在每次迭代后，当前批量样本的局部级特征和全局级特征会分别入队到$M_I^L$/$M_I^G$中，这可推导为：
{MIL=MIL∪{FIij∣j∈[1,Nm],i∈[1,Nb]}MIG=MIG∪{GIi∣i∈[1,Nb]}.(7)\left\{ \begin{aligned} M_I^L &= M_I^L \cup \{ F_{I_i}^j \mid j \in [1, N_m], i \in [1, N_b] \} \\ M_I^G &= M_I^G \cup \{ G_{I_i} \mid i \in [1, N_b] \}. \end{aligned} \right. \tag{7} {MIL​MIG​​=MIL​∪{FIi​j​∣j∈[1,Nm​],i∈[1,Nb​]}=MIG​∪{GIi​​∣i∈[1,Nb​]}.​(7)
  同时，当$M_I^L$/$M_I^G$的长度大于$n_I^G$/$n_I^L$时，会从$M_I^L$/$M_I^G$中弹出与入队特征长度相同的“最久追加特征”，以保持记忆库中的特征是最新的。

1. 记忆库的本质
  动态存储特征的“队列” 记忆库（如局部记忆库 $M^L$、全局记忆库$M^G$）是一个有限容量的存储结构，用来保存“有代表性的特征”（如patch级特征、全局实例特征）。它的核心作用是通过“存储最新特征”，为后续的“紧致性优化”提供最新的特征分布参考。
2. “长度相同”的含义
  保持记忆库容量稳定 当新特征（“入队特征”）被添加到记忆库时，若记忆库当前长度（存储的特征数量）超过预设阈值（如$n_G^L$或$n_L^G$），就需要弹出等量的旧特征，从而保证记忆库的总容量（特征数量）不变。
  这里的“长度相同”，指的是 “入队的新特征数量”与“弹出的旧特征数量”相等，以此维持记忆库的容量稳定。
3. “最久追加特征”的定义
  最早加入的旧特征 “最久追加特征”指记忆库中最早被添加（追加）进去的特征。
   因为记忆库要服务于“当前任务的最新特征分布”，所以需要持续 “淘汰最旧的特征，引入最新的特征” ——当新特征入队时，弹出“最久前加入的旧特征”，就能让记忆库始终保留 相对最新的特征集合 ，避免用过时的特征指导优化。
4.举个直观例子
  假设局部记忆库$M^L$最多存$100$个patch级特征（容量阈值）：

• 当新产生$5$个patch特征需要“入队”时，记忆库当前长度会超过$100$；
• 此时需要弹出$5$个“最久追加”的旧特征（即最早被存入$M^L$ 的$5$个特征）；
• 最终记忆库仍存$100$个特征，且是“相对最新”的一批。

  
   简言之：记忆库通过“入队新特征 + 弹出等量最久旧特征”的方式，维持容量稳定且保留最新特征，从而为后续的紧致性优化提供有效参考。

  对点云特征{FPi}i=1Nb\{F_{P_i}\}_{i=1}^{N_b}{FPi​​}i=1Nb​​也执行类似的全局和局部紧致性优化操作，且点云特征的全局、局部记忆库大小与RGB模态一致。
  因此，所提出的IFC的损失函数可总结为：
$${\mathcal{L}}_{\text{IFC}}={\mathcal{L}}_{\text{LC}}+{\mathcal{L}}_{\text{GC}}.\text{\hspace{1em}(8)}$$
  综上，所提出的LSFA的整体训练损失 推导为：
$${\mathcal{L}}_{\text{LSFA}}={\mathcal{L}}_{\text{IFC}}+\lambda {\mathcal{L}}_{\text{CLC}}.\text{\hspace{1em}(9)}$$
  其中$\lambda$是用于平衡的超参数。

3.4. Defect Localization 缺陷定位

3.4.1 算法

  由于 LSFA 旨在通过适配预训练特征来更好地估计异常模式，我们利用预训练骨干网络和适配器进行最终特征提取。两种模态的适配后特征分别被输入到现成的、基于特征嵌入的方法 PatchCore[26] 中。对两种模态的异常分数取平均，作为每个像素/体素的最终异常分数，以评估异常检测的效果。LSFA 的整体伪代码可参见算法1。

3.4.2 Discussion 讨论

  由于 LSFA 的框架与 M3DM [31] 相似，在此我们详细讨论它们的差异。首先，与 [31] 中引入额外模块进行特征提取不同，我们仅对每个模态执行特征适配，且不需要额外的记忆库，因此在推理时不会引入额外的时间和内存开销。
  此外，M3DM 忽视了面向精准异常检测的“物体级特征对齐”的重要性。而我们的 LSFA 从物体级和 patch 级两个视角执行跨模态特征对齐，以充分增强跨模态判别性信息的一致性与交互性，因此表现出比它优越得多的性能。
  最后，LSFA 还考虑了==“模态内特征紧致性”==，这也是 M3DM 所忽略的。具体而言，与跨模态对齐类似，模态内特征紧致性优化也从 patch 级和物体级两个视角开展，以 缓解预训练特征的领域偏差影响，并获得高质量的单模态特征。

4. Experiments 实验

4.1. Experimental Details 实验细节

4.1.1 Dataset 数据集

  为验证 LSFA 的有效性，我们在两个 3D 工业异常检测数据集上开展实验：MVTec-3D AD[4] 和 Eyecandies[6]。数据集的详细信息在我们的补充材料中阐述。

4.1.2 Implementation details 实现细节

  对于 RGB 模态的特征提取器，采用在 ImageNet [11] 上经 DINO [7] 预训练的 ViT-B/8 [12]，以在效率与性能间取得平衡。最终层的输出为 768 维，用于后续特征提取。对于3D 模态的特征提取，使用在 ShapeNet [8] 数据集上预训练的 Point Transformer [23]，并拼接 3/7/11 层的输出以融合多尺度信息，从而进行更精细的调整。
  与 ViT 类似，Point Transformer 将点云划分为多个局部组，这些组有对应的中心点（用于定位）和邻居数量（用于组大小）。在 RGB 数据处理时，通过 RANSAC [13] 估计深度图像的背景平面来去除背景区域，其中忽略$5\times 10^{-2}$以内的点，以加速特征提取、均值计算并减轻背景的影响。
  最后，RGB 图像和点云张量均被调整为$224\times 224$，与输入尺寸一致。CLC 中用于点云和 RGB 样本的投影特征为 512 维。使用AdamW 优化器，其学习率设为$2\times 10^{-3}$，并采用余弦热身策略（cosine warm-up）。自适应批量大小$N_b$设为 8。

4.1.3 Evaluation metrics 评估指标

  遵循 MVTec-3D 和 Eyecandies 的标准评估协议，我们使用图像级 ROC 曲线下面积（I-AUROC）、像素级 AUROC（P-AUROC），以及每个区域的异常检测性能（AUPRO）。
  I-AUROC/P-AUROC 定义为图像级/像素级预测的接收者操作特征曲线下面积，而 AUPRO 表示二值预测与每个真实标签连通区域的平均相对重叠。

4.2. Comparison on 3D AD Benchmark 3D异常检测基准测试对比

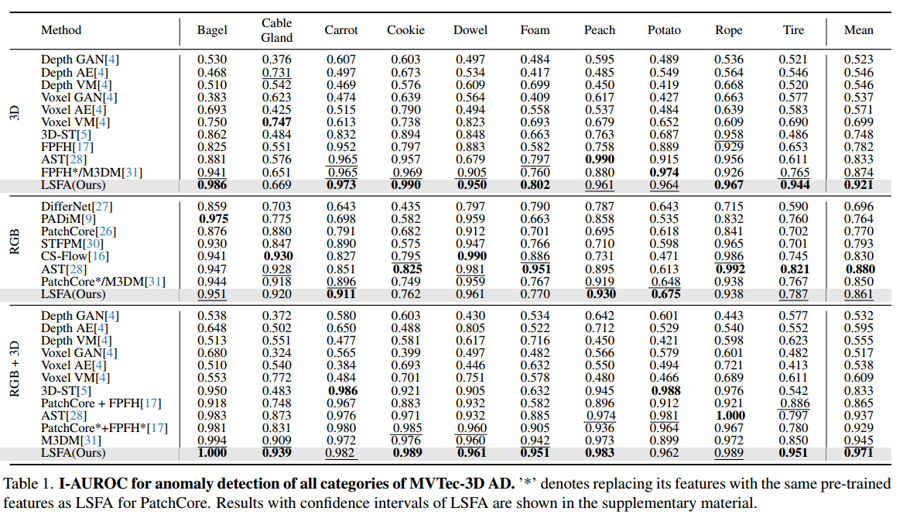
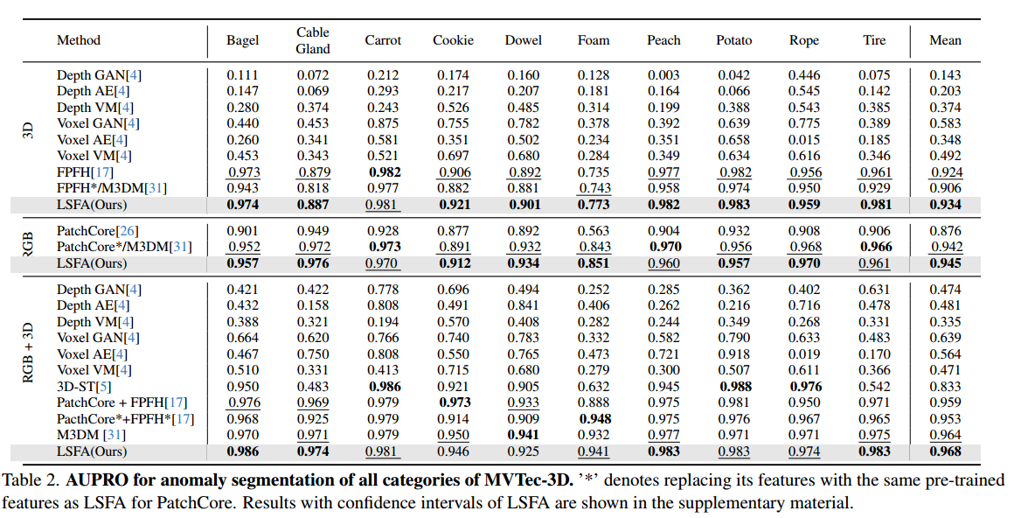
  为全面评估我们方法的有效性，我们首先在MVTec-3D AD数据集上，针对3D、RGB、3D+RGB三种模态均开展实验。表1和表2展示了I-AUROC与AUPRO的对比结果，方法按模态分组（我们也在补充材料中报告了P-AUROC）。

4.2.1 I-AUROC指标

  1）在I-AUROC指标方面，我们的方法不仅能为单模态基准测试中的基线方法带来显著提升，也能在多模态组合的基准测试中实现这一点，尤其对于具有挑战性的类别（如电缆密封套、轮胎）。单模态的结果表明，我们的模态内特征紧致性优化有效提升了特征质量，进而在推理过程中助力异常定位。此外，在所有类别平均值上，我们的方法以较大幅度显著优于以往所有方法——3D模态提升了4.7%，多模态组合提升了4.2%。在涉及所有类别和数据模态的全部30个案例中，有17个案例实现了新的最先进（state-of-the-art） 性能。

4.2.2 AUPRO指标

  2）在AUPRO指标方面，LSFA在异常分割任务中也能持续取得高于以往所有方法的分数，这表明我们的方法更善于挖掘局部化且细致的线索，以发现关键的意外模式。除MVTec-3D AD外，我们还在最新的大规模3D异常检测数据集Eyecandies上进行了详细评估。相应结果见补充材料，其中我们的方法取得最佳结果，显著优于所有以往方法，在RGB模态上分别实现了平均I-AUROC为87.5%、平均AUPRO为97.8%。

4.3. Ablation Study 消融研究

  为探究所提出的 LSFA 中各组件的影响，我们在 MVTec-3D上开展消融分析。

4.3.1 Investigation on IFC. 对 IFC 的研究

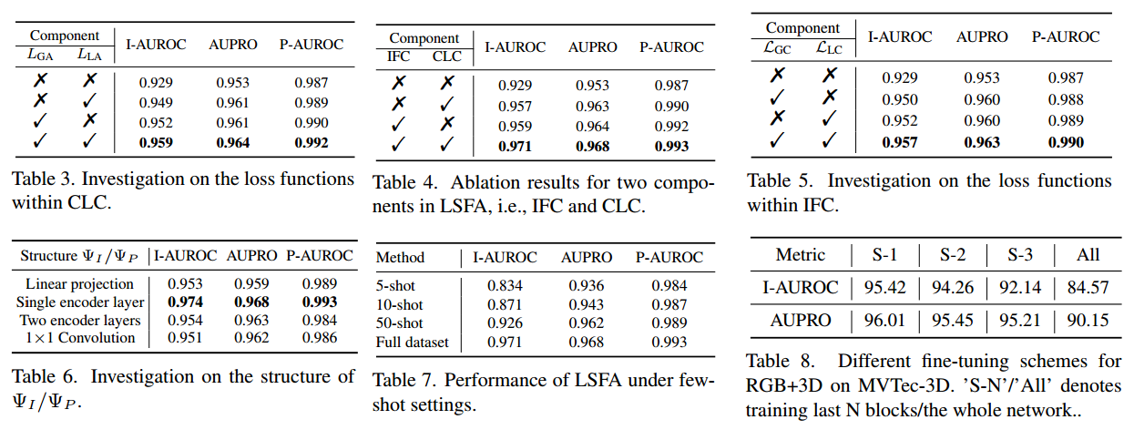
  首先分析所提 IFC 的影响。将“直接使用预训练特征、未做适配的 PatchCore 方法”作为所有评估的基线。如表 4 所示，仅用固定预训练特征的基线方法在所有指标上准确率均较差。相比之下，IFC 通过显式优化特征紧致性，并与推理过程保持一致，带来了显著的性能提升（I-AUROC/AUPRO 分别提升约 2.8%/1.0%），这增强了特征对异常模式的敏感性。表 5 详细分析了 IFC 内的每个损失项，其中全局和局部紧致性损失均对最终性能有贡献。

4.3.2 Investigation on CLC 对 CLC 的研究

  接着探究 CLC 的影响。如表 4 所示，CLC 通过执行多粒度跨模态对比表示学习，也取得了与 IFC 相近的准确率。这主要是因为所提 CLC 能从多视角有效缓解“模态间错位”的影响，同时利用特征提取的自监督信号。
  类似地，表 3 展示了 CLC 各子组件的结果：其中全局和局部跨模态对比损失，相较于基线方法均提升了性能。
  此外，结合 IFC 和 CLC 后，准确率还能进一步提高。上述结果验证了所提 IFC、CLC 及其各自关键组件的有效性。

4.3.3 Qualitative results 定性结果

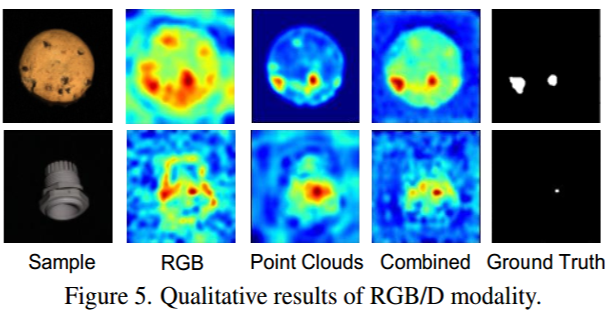
  我们进一步开展定性实验，探究 RGB/3D 模态的影响。图 5 展示了 RGB、3D、多模态组合的预测结果：

• RGB 模态的结果更分散，且在边缘区域也会赋予较高分数；
• 3D 模态的分数分布则更集中在缺陷周围；
• 多模态组合的结果表明，两种模态的结合有助于精准定位缺陷。
• 

4.3.4 Parameter sensitivity 参数敏感性

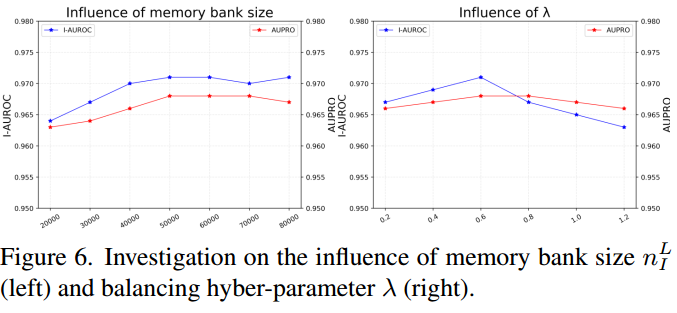
  接下来，评估方法中几个重要超参数的敏感性，包括记忆库大小$n_F^L$和平衡因子$\lambda$：

• 如图 6（左）所示， LSFA 在所有记忆库尺寸下性能相近，因此对$n_F^L$不敏感 。为平衡性能与内存开销，将$n_F^L$设为$5\times 10^4$；
• 关于$\lambda$的影响，图 6（右）表明 LSFA 对$\lambda$的值也不敏感 。由于更大的$\lambda$会导致性能略有下降，因此将$\lambda$设为 0.6 以获得最佳结果。
  

4.3.5 Investigation on adaptor structure 对适配器结构的研究

  如表 6 所示，除上述实验外，最后探究不同适配器结构的影响（包括线性投影层、单个普通 Transformer 编码器层、多个普通 Transformer 编码器层、$1\times 1$卷积层）。其中，单个普通 Transformer 编码器层在这些结构中表现最佳。

4.4. Few-shot Anomaly Detection 少样本异常检测

  如表7所示，为评估我们的方法在极端场景下的有效性，我们在少样本设置下开展实验。具体而言，我们从每个类别中随机抽取5张、10张或50张图像作为训练集，并在整个测试集上进行评估。结果表明，我们的方法仍能取得优异性能，即便与表1中用完整训练集训练的方法相比也是如此。此外，也可采用不同的微调方法（例如LoRA [19]）。

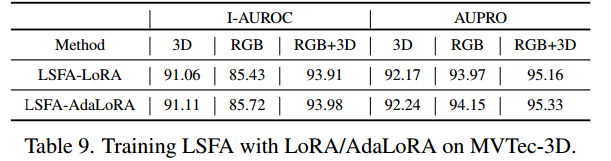
4.5. Comparison with Fine-tuning Methods 与微调方法的对比

  在此，我们移除适配器${\varphi }_I/{\varphi }_P$，并将 LSFA 与现成的微调方法 LoRA [19] 和 PEFT 中的 AdaLoRA [36] 相结合。结果如表 9 所示，这些结果略逊于我们的 LSFA 方法的结果。我们移除适配器，并分别评估在 LSFA 中“训练整个网络”和“训练骨干网络最后几个阶段”的结果。如表 8 所示，随着更多模块被用于训练，观察到更严重的性能下降，尤其是在训练所有模块时。这种现象表明，仅训练部分模块或不固定任何模块会导致严重的灾难性遗忘，并对特定数据域过拟合，从而无法区分异常模式与正常模式。

5. Conclusion 结论

  在本文中，我们提出了 LSFA，这是一个用于多模态异常检测的简单且有效的自监督多模态特征适配框架。具体而言，LSFA 在模态内和模态间两个方面进行特征适配：对于前者，提出了一种基于动态更新记忆库的特征紧致性优化方法，以增强特征对异常模式的敏感性；对于后者，提出了一种局部到全局的一致性对齐策略，用于多尺度跨模态信息交互。大量实验表明，我们的方法比以往方法取得了优异得多的性能，同时显著提升了现有的基于特征嵌入的基线方法。