[数据结构总结篇]--线性表
| 函数返回类型 | return 语句的规则 | 示例 |
|---|---|---|
int | 必须写 return,且后面必须跟一个 int 类型的值 | return i;、return 0; |
void | 可以不写 return;若写 return,后面不能跟值 | return;(正确)、return 1;(错误) |
存储结构一:顺序存储---顺序表
一.插入
1.1尾插 O(1)--一个元素动
n为元素个数 ++n就是最后一个元素了 让最后一个元素变成x
实现:
void push_back(int x){a[++n]=x;}测试:
int main( ){push_back(2);print();push_back(5);print();return 0;}1.2头插 O(n)--从后往前右移
[1,n]后移一位--第一个元素是x---元素个数++
实现:
void push_front(int x){for(int i=n;i>=1;i--){a[i+1]=a[i];}a[1]=x;n++;}测试:
int main( ){push_front(2);print();push_front(5);print();return 0;}
for(int i=1;i<=n;i++){ // 错误!会导致元素覆盖,数据丢失
a[i+1]=a[i];
}
错误原因:从 i=1 开始后移,会先把 a[2] 覆盖成 a[1],再把 a[3] 覆盖成 a[2](也就是原来的 a[1]),最终所有元素都会变成初始 a[1] 的值(比如原数组 [ ,10,20],循环后会变成 [ ,10,10])。
正确循环:必须从 最后一个元素 开始往后移,避免覆盖,循环条件应为 i从n开始,到1结束:
1.3p位置插入 O(n)--[p,n]元素从后往前右移
!!!传入位置p啊啊啊
void insert(int p,int x){for(int i=n;i>=p;i--){a[i+1]=a[i];}a[p]=x;n++;}二.删除
2.1尾删 O(1)
把n从4变成3
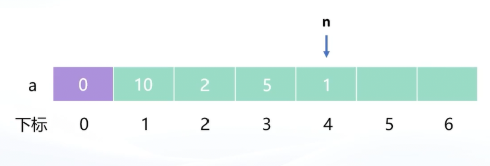
void pop_back(){if(n == 0) return; // 空表不操作n--;
}或
void pop_back(){n--;
}2.2头删 O(n) 从前往后左移
从[2,n]数据全部后移 ---元素个数-1---后一个=前一个值
void pop_front(){ //不用传参了for(int i=2;i<=n;i++){ //写错过a[i-1]=a[i];}n--;}正确的 "删除首元素" 逻辑应该是:
从前往后统一向左移动 所以从i=2
删除首元素(a[1])后,需要把后面的元素依次向前移动(覆盖前面的位置),最终元素个数减 1。
例如,原数组是 [ ,10,20,30,40](n=4),删除首元素后应该变成 [ ,20,30,40, ](n=3)。
移动过程是:
a[1] = a[2](用 20 覆盖 10)
a[2] = a[3](用 30 覆盖 20)
a[3] = a[4](用 40 覆盖 30)
删除首元素需要 "后面的元素往前补",所以是 a[i-1] = a[i];如果是插入首元素(push_front),才需要 "前面的元素往后移",用 a[i+1] = a[i]。
2.3p位置删除 O(n) [p+1,n]从前往后左移
void erase(int p){//i从[p+1,n]统一左移一位 for(int i=p+1;i<=n;i++){a[i-1]=a[i];}n--;
}一、先明确 “正确的任意位置删除逻辑”
假设数组是 [ ,10,20,30,40](n=4),要删除第 p=2 个元素(值为 20),最终结果应该是 [ ,10,30,40, ](n=3)。
关键步骤是:只需要移动 p 后面的元素(即从 p+1 到 n 的元素),让它们向左 “补位”:
a[2] = a[3](用 30 覆盖被删除的 20)a[3] = a[4](用 40 覆盖原来的 30)
这里的移动范围是i从p+1开始,到n结束,赋值逻辑是a[i-1] = a[i](左移 1 位)。
二、为什么第一个 erase(int p) 是对的?
第一个函数的循环是:
for(int i = p+1; i <= n; i++){ // 循环范围:p+1 到 na[i-1] = a[i]; // 左移:i-1(前一个位置) = i(当前位置)
}
- 循环只处理
p后面的元素(p+1到n),不碰p前面的元素(避免无效操作); - 赋值
a[i-1] = a[i]正好让每个元素向左移 1 位,完美覆盖被删除的p位置。
用上面的例子(删 p=2)验证:
i从3(p+1=2+1)开始,到4(n=4)结束:i=3:a[2] = a[3]→ 20 变成 30;i=4:a[3] = a[4]→ 30 变成 40;
- 最终数组正确,
n--后元素个数从 4 变 3,完全正确。
三、为什么第二个 erase(int p,int x) 是错的?
这个函数有 两个致命问题,直接破坏了删除逻辑:
问题 1:多传了无用参数 int x
“任意位置删除” 只需要知道 要删除的位置 p 即可(比如删第 2 个、第 3 个),根本不需要传入 x(x 在这里没有任何用途,反而会导致调用时必须多传一个无关的值,比如 erase(2, 0),完全多余且不规范)。
问题 2:循环范围错误,导致删除位置偏移
第二个函数的循环是:
for(int i = p; i <= n; i++){ // 循环范围:p 到 n(错误!)a[i-1] = a[i];
}
循环从 p 开始,而不是 p+1,会导致 把 p 位置本身也卷进移动,最终删除的是 p-1 位置的元素,而非目标 p 位置。
还是用 “删 p=2(20)” 的例子验证:
i从2(p=2)开始,到4(n=4)结束:i=2:a[1] = a[2]→ 10 变成 20(原本要保留的 10 被覆盖了!);i=3:a[2] = a[3]→ 20 变成 30;i=4:a[3] = a[4]→ 30 变成 40;
- 最终数组变成
[ ,20,30,40, ](n=3),相当于删除了p=1位置的 10,而不是目标p=2位置的 20,完全不符合预期!
四、总结:两个 erase 的核心区别
| 函数 | 循环范围 | 是否多传参数 | 最终效果 |
|---|---|---|---|
erase(int p) | p+1 ~ n | 否 | 正确删除第 p 个元素 |
erase(int p,int x) | p ~ n | 是(多传 x) | 错误删除第 p-1 个元素 |
简单记:删除第 p 个元素,只需要移动 p 后面的元素(p+1 到 n),第一个函数做到了,第二个函数因为循环范围错了(从 p 开始),所以删错了位置,再加上多余的 x 参数,自然就是错的~
三.查找
3.1按值查找 O(n)
int find(int x){for(int i=1;i<=n;i++){if(a[i]==x) return i;} //== i返回下标return 0;}3.2按位查找 O(1)
int at(int p){return a[p];}
int at(int p) {if (p < 1 || p > n) { // 检查p是否在有效范围内return -1; // 或其他错误标识(根据你的需求定义)}return a[p];
}四.修改 O(1)
void change(int p,int x){a[p]=x;}五.清空
void clear(){n=0;}