scikit-learn 分层聚类算法详解
scikit-learn 分层聚类算法详解
本文介绍了 scikit-learn 的 AgglomerativeClustering 分层聚类算法。该方法通过逐步合并相似样本形成层次结构,参数如 n_clusters、linkage、metric 等影响聚类效果。文中对比了多种 linkage 方法并可视化结果,展示其差异与适用场景。结论指出:分层聚类直观可解释,但在大规模数据中计算开销较大。
1. 算法背景
分层聚类(Hierarchical Clustering)是一类基于样本之间相似性逐步聚合或拆分的无监督学习方法。
在 scikit-learn 中,其核心实现类是 AgglomerativeClustering,即 凝聚型分层聚类:
- 自底向上:每个样本先作为独立簇,逐步合并,直到满足设定条件。
- 结果可通过 树状结构(dendrogram) 表示样本合并的层次关系。
这类算法在小规模数据分析、可视化探索和树状关系建模中有天然优势。
2. 数学模型与合并策略
2.1 数学模型
给定样本集:
X={x1,x2,…,xn},xi∈Rd
X = \{x_1, x_2, \dots, x_n\}, \quad x_i \in \mathbb{R}^d
X={x1,x2,…,xn},xi∈Rd
目标是得到一个分层的树状结构(dendrogram)。算法主要依赖 簇间距离度量:
设簇 Ca,CbC_a, C_bCa,Cb,簇间距离定义方式有多种(即 linkage 方法):
-
单链接 (single linkage):
D(Ca,Cb)=minx∈Ca,y∈Cb∥x−y∥D(C_a, C_b) = \min_{x \in C_a, y \in C_b} \|x - y\|D(Ca,Cb)=x∈Ca,y∈Cbmin∥x−y∥
-
全链接 (complete linkage):
D(Ca,Cb)=maxx∈Ca,y∈Cb∥x−y∥D(C_a, C_b) = \max_{x \in C_a, y \in C_b} \|x - y\|D(Ca,Cb)=x∈Ca,y∈Cbmax∥x−y∥
-
平均链接 (average linkage):
D(Ca,Cb)=1∣Ca∣∣Cb∣∑x∈Ca∑y∈Cb∥x−y∥D(C_a, C_b) = \frac{1}{|C_a||C_b|} \sum_{x \in C_a} \sum_{y \in C_b} \|x-y\|D(Ca,Cb)=∣Ca∣∣Cb∣1x∈Ca∑y∈Cb∑∥x−y∥
-
Ward 方法(默认,最常用):
D(Ca,Cb)=∣Ca∣∣Cb∣∣Ca∣+∣Cb∣∥μa−μb∥2D(C_a, C_b) = \frac{|C_a||C_b|}{|C_a| + |C_b|}\|\mu_a - \mu_b\|^2D(Ca,Cb)=∣Ca∣+∣Cb∣∣Ca∣∣Cb∣∥μa−μb∥2
其中 μa,μb\mu_a,\mu_bμa,μb 分别为簇均值。Ward 方法通过最小化类内方差增量来选择合并,因而最常用。
2.2 不同 linkage 策略的对比
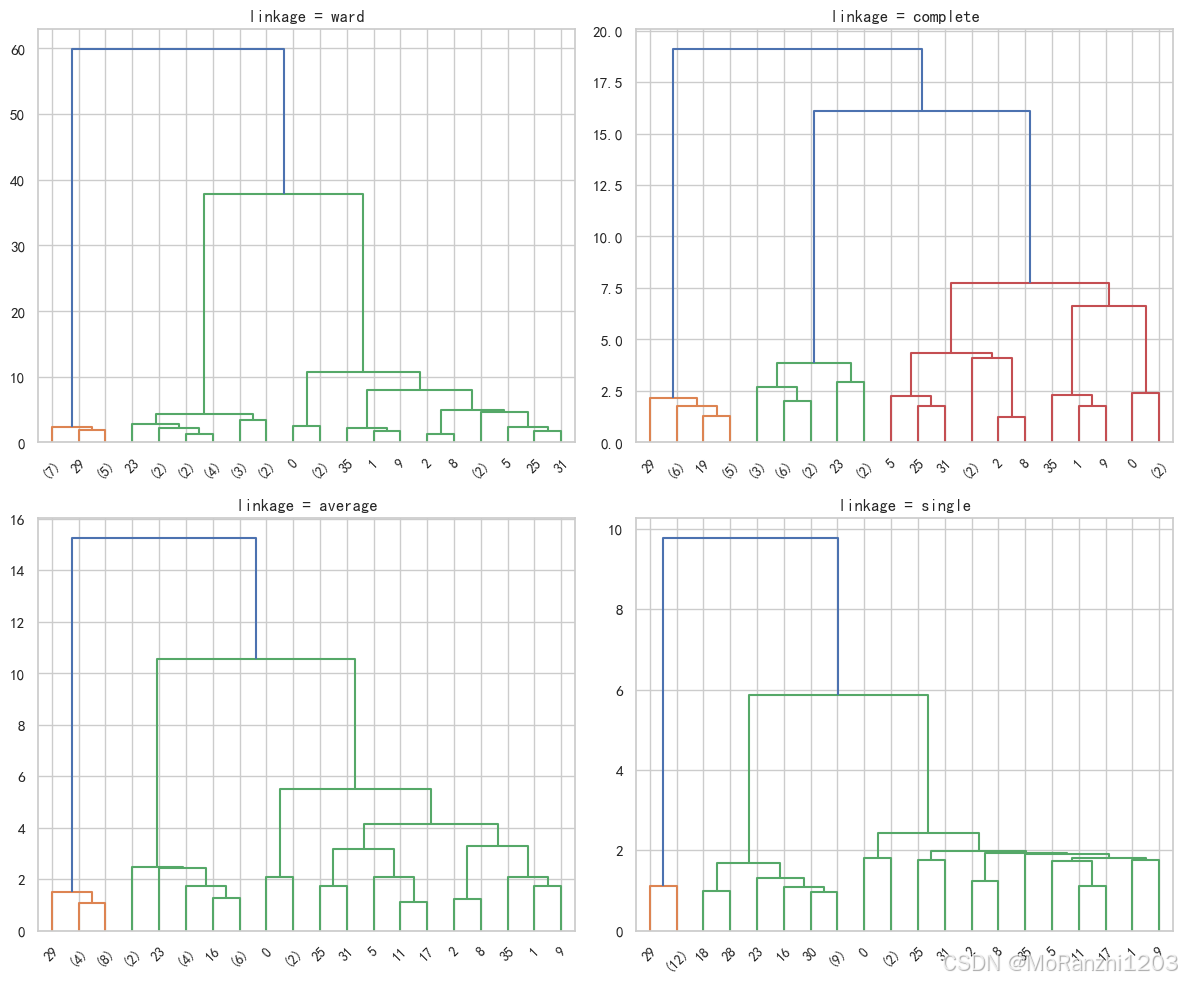
使用 scipy.cluster.hierarchy.linkage + dendrogram 可以直观对比不同策略下的树状图:
- Ward:聚类较均衡。
- Complete:合并更谨慎,层级更高。
- Average:折中方案。
- Single:易出现“链式效应”。
这种差异在数据形态复杂时尤为明显。
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.datasets import make_blobs# 生成数据(更容易体现 linkage 差异)
X, _ = make_blobs(n_samples=40, centers=3, cluster_std=[1.0, 2.5, 0.5], random_state=42)linkages = ["ward", "complete", "average", "single"]
fig, axes = plt.subplots(2, 2, figsize=(12, 10))for ax, method in zip(axes.flat, linkages):# 计算层次聚类树Z = linkage(X, method=method)dendrogram(Z, ax=ax, truncate_mode="lastp", p=20, leaf_rotation=45, leaf_font_size=10)ax.set_title(f"linkage = {method}")plt.tight_layout()
plt.show()
3. 实现流程
层次聚类的执行过程通常包括:
- 初始化:每个样本为一个簇。
- 计算距离矩阵:得到所有簇之间的距离。
- 合并最近簇:根据 linkage 策略选择最近的两个簇合并。
- 更新距离矩阵:重新计算新簇与其他簇的距离。
- 循环迭代:直到达到设定簇数
n_clusters,或所有点合并为一个簇。
4. AgglomerativeClustering 的主要参数
from sklearn.cluster import AgglomerativeClusteringmodel = AgglomerativeClustering(n_clusters=2,metric='euclidean',memory=None,connectivity=None,compute_full_tree='auto',linkage='ward',distance_threshold=None,compute_distances=False
)
n_clusters:目标簇数,默认 2。若设置了distance_threshold,需设为None。metric:距离度量方式(默认欧氏距离)。注意ward仅支持欧氏距离。memory:缓存路径或joblib对象,用于加速重复计算。connectivity:约束可连接的点对(常用于图像/空间数据)。compute_full_tree:是否构建完整层次树。'auto'会根据参数自动选择。linkage:合并策略,可选'ward'、'complete'、'average'、'single'。distance_threshold:基于距离的停止条件。若设置,则由阈值决定簇数。compute_distances:是否存储簇间距离,用于绘制 dendrogram。
5. 样例说明
以鸢尾花 (Iris) 数据集为例:
from sklearn.datasets import load_iris
from sklearn.cluster import AgglomerativeClustering
from sklearn.decomposition import PCA
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np# =====================
# 1. 设置绘图风格
# =====================
sns.set_theme(style="whitegrid", font="SimHei", rc={"axes.unicode_minus": False})# =====================
# 2. 加载鸢尾花数据
# =====================
iris = load_iris()
X = iris.data # 特征矩阵
y = iris.target # 真实标签(Setosa, Versicolor, Virginica)# =====================
# 3. 建立分层聚类模型
# =====================
clustering = AgglomerativeClustering(n_clusters=3, linkage='ward')
labels = clustering.fit_predict(X) # 聚类标签(0,1,2)# =====================
# 4. PCA降维到2维,便于可视化
# =====================
X_pca = PCA(n_components=2).fit_transform(X)# =====================
# 5. 用KNN近似聚类边界
# 因为 AgglomerativeClustering 没有 predict 方法
# → 用 KNN 拟合聚类标签,从而生成分区边界
# =====================
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_pca, labels)# 创建网格(覆盖整个二维空间)
x_min, x_max = X_pca[:, 0].min() - 0.5, X_pca[:, 0].max() + 0.5
y_min, y_max = X_pca[:, 1].min() - 0.5, X_pca[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300),np.linspace(y_min, y_max, 300))# 预测网格点的聚类结果,用于绘制边界
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)# =====================
# 6. 创建一行两列子图(共享坐标轴范围)
# =====================
fig, axes = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)# ---------------------
# 左图:原始数据(按真实类别着色)
# ---------------------
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=y,palette="Set1", s=70, ax=axes[0],edgecolor="k", linewidth=0.6)
axes[0].set_title("原始鸢尾花数据 (真实类别)", fontsize=12)
axes[0].grid(True, linestyle="--", linewidth=0.7) # 设置虚线网格
leg0 = axes[0].legend(loc="lower right", frameon=True) # 图例右下角
leg0.get_frame().set_facecolor('white') # 设置白色底# ---------------------
# 右图:分层聚类结果(加上聚类边界)
# ---------------------
# 背景分区填充
axes[1].contourf(xx, yy, Z, alpha=0.2, cmap="Set2")
# 聚类边界线
axes[1].contour(xx, yy, Z, colors='k', linewidths=0.8)
# 数据点(聚类结果着色)
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=labels,palette="Set2", s=70, ax=axes[1],edgecolor="k", linewidth=0.6)
axes[1].set_title("分层聚类结果 (含边界)", fontsize=12)
axes[1].grid(True, linestyle="--", linewidth=0.7)
leg1 = axes[1].legend(loc="lower right", frameon=True)
leg1.get_frame().set_facecolor('white')# =====================
# 7. 保持两个子图坐标范围一致
# =====================
axes[0].set_xlim(x_min, x_max)
axes[0].set_ylim(y_min, y_max)plt.tight_layout()
plt.show()
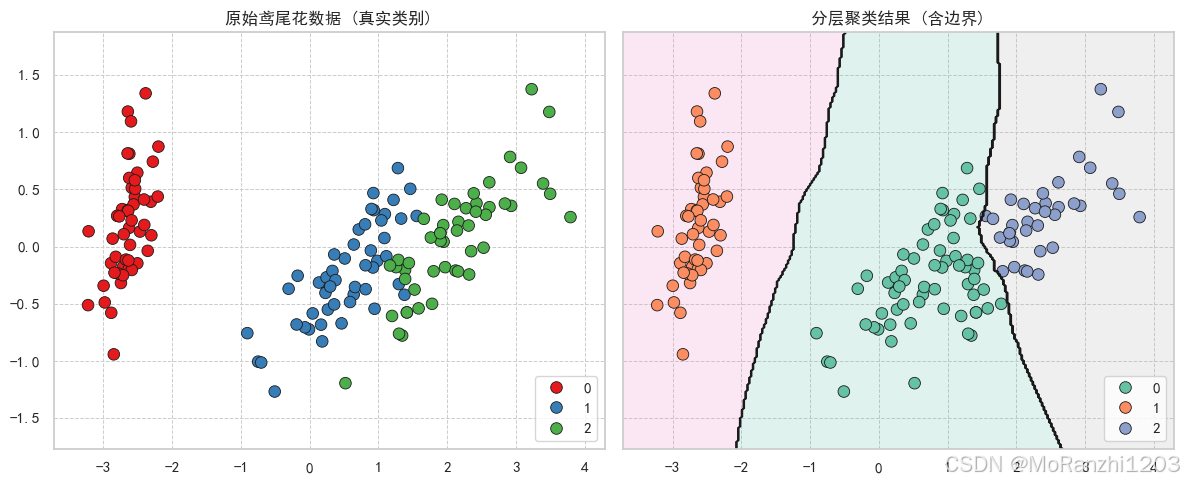
运行结果中,不同颜色代表模型划分出的簇,能大致对应真实鸢尾花种类。
6. 应用场景
AgglomerativeClustering 常用于:
- 生物信息学:基因表达谱分析(热力图 + 树状图)。
- 文本挖掘:文档相似度分析,形成分层主题。
- 图像处理:小规模图像的颜色/区域分割。
- 社会网络分析:探索群体结构与分层关系。
- 市场研究:消费者分层与行为建模。
7. 总结
AgglomerativeClustering是scikit-learn提供的 分层聚类核心工具。- 它通过灵活的
linkage与distance_threshold,可以实现多样化的分层划分。 - 优点:结果直观、可解释性强。
- 缺点:在大规模数据上计算成本高。
适用于 小规模数据的探索性分析、可视化和结构建模,在实际应用中非常常见。
