当前位置：首页 > news >正文

P4342 [IOI 1998] Polygon -普及+/提高

news 2025/9/14 19:11:40

P4342 [IOI 1998] Polygon

题目描述

题目可能有些许修改，但大意一致。

Polygon 是一个玩家在一个有 $n$ 个顶点的多边形上玩的游戏，如图所示，其中 $n = 4$ 。每个顶点用整数标记，每个边用符号 +（加）或符号 *（乘积）标记。

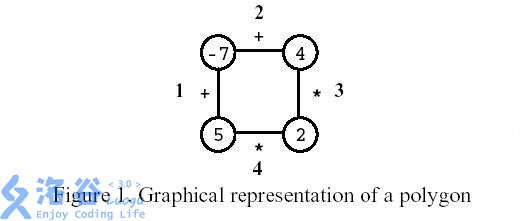
第一步，删除其中一条边。随后每一步：

选择一条边连接的两个顶点 $V_1$ 和 $V_2$ ，用边上的运算符计算 $V_1$ 和 $V_2$ 得到的结果来替换这两个顶点。

游戏结束时，只有一个顶点，没有多余的边。

如图所示，玩家先移除编号为 $3$ 的边。之后，玩家选择计算编号为 $1$ 的边，然后计算编号为 $4$ 的边，最后，计算编号为 $2$ 的边。结果是 $0$ 。

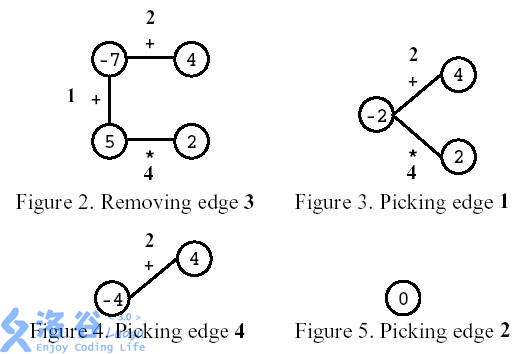
（译者注：这里每条边的运算符旁边的数字为边的编号，不拿来计算）

编写一个程序，给定一个多边形，计算最高可能的分数。

输入格式

输入描述一个有 $n$ 个顶点的多边形，它包含两行。第一行是数字 $n$ ，为总边数。

第二行描述这个多边形，一共有 $n$ 组，每组中第一个字符为边 $i$ 的计算符号（t 代表相加，x 代表相乘），第二个代表顶点 $i$ 上的数字。多边形首尾相连。

输出格式

第一行，输出最高的分数。在第二行，输出所有可能的在第一步即被清除后仍能得到最高分的边的下标，以严格升序输出。

输入输出样例 #1

输入 #1

4
t -7 t 4 x 2 x 5

输出 #1

33
1 2

说明/提示

保证 $\le n \le 50$ 。

对于任何一系列的操作，顶点数字都在 $[- 32768, 32767]$ 的范围内。

solution

动态规划

1 定义公式

 f[i][j] ：合并 [i, j] 能获得的最大值

 g[i][j] ：合并 [i, j] 能获得的最小值

2 递推关系
- 如果是加号
  f[i][j] = max(f[i][k-1] + f[k][j])
  g[i][j] = max(g[i][k-1] + g[k][j])
- 如果是乘号
  f[i][j] = max(f[i][k-1] * f[i][k-1], g[i][k-1] * g[i][k-1], f[i][k-1] * g[i][k-1], g[i][k-1] * f[i][k-1])
  g[i][j] = min(f[i][k-1] * f[i][k-1], g[i][k-1] * g[i][k-1], f[i][k-1] * g[i][k-1], g[i][k-1] * f[i][k-1])
3 结果
- 最大值 max(f[i][i + len - 1])
- 取大值时 i 即为最开始去掉边

代码

#include "algorithm"
#include "iostream"
#include "unordered_map"
#include "cstring"using namespace std;/** P4342 [IOI 1998] Polygon* 题目大意：* 有一个n(3<=n<=50)的点的环，每个点是一个数，每条边是一个符号(+ or *)。一开始去除一条边。* 然后每次可以去除一条边将两个点合并。问结果最大是多少，最大值对应的最开始去除的是哪个边** 思路：动态规划* 1 定义公式*      f[i][j] ：合并 [i, j] 能获得的最大值*      g[i][j] ：合并 [i, j] 能获得的最小值* 2 递推关系*      如果是加号*          f[i][j] = max(f[i][k-1] + f[k][j])*          g[i][j] = max(g[i][k-1] + g[k][j])*      如果是乘号*          f[i][j] = max(f[i][k-1] * f[i][k-1], g[i][k-1] * g[i][k-1], f[i][k-1] * g[i][k-1], g[i][k-1] * f[i][k-1])*          g[i][j] = min(f[i][k-1] * f[i][k-1], g[i][k-1] * g[i][k-1], f[i][k-1] * g[i][k-1], g[i][k-1] * f[i][k-1])* 3 结果*      最大值 max(f[i][i + len - 1])*      取大值时 i 即为最开始去掉边*/int f[55][55], g[55][55], n, a[55], ans, t, st[55];
char op[55];int main() {cin >> n;memset(f, 0x80, sizeof f);memset(g, 0x7f, sizeof g);for (int i = 0; i < n; i++) cin >> op[i] >> a[i], f[i][i] = a[i], g[i][i] = a[i];for (int len = 2; len <= n; len++) {for (int i = 0; i < n; i++) {int j = i + len - 1;for (int k = i + 1; k <= j; k++)if (op[k % n] == 't') {f[i][j % n] = max(f[i][j % n], f[i][(k + n - 1) % n] + f[k % n][j % n]);g[i][j % n] = min(g[i][j % n], g[i][(k + n - 1) % n] + g[k % n][j % n]);} else {f[i][j % n] = max({f[i][j % n], f[i][(k + n - 1) % n] * f[k % n][j % n],f[i][(k + n - 1) % n] * g[k % n][j % n], g[i][(k + n - 1) % n] * f[k % n][j % n],g[i][(k + n - 1) % n] * g[k % n][j % n]});g[i][j % n] = min({g[i][j % n], f[i][(k + n - 1) % n] * f[k % n][j % n],f[i][(k + n - 1) % n] * g[k % n][j % n], g[i][(k + n - 1) % n] * f[k % n][j % n],g[i][(k + n - 1) % n] * g[k % n][j % n]});}if (len == n) {if (f[i][j % n] > ans) ans = f[i][j % n], t = 0, st[t++] = i;else if (f[i][j % n] == ans) st[t++] = i;}}}cout << ans << endl;for (int i = 0; i < t; i++) cout << st[i] + 1 << ' ';return 0;
}