Qwen3-80B-A3B混合注意力机制

一、注意力机制背景：
在Transformer架构中，自注意力（Self-Attention）是核心组件。其基本公式为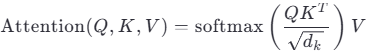： 其中：
Q (Query)：查询向量，表示问询量。用于与其他位置的Key交互，计算相似度
K (Key)：键向量，用于匹配查询的特征
V (Value)：值向量，是最终被加权求和的内容
dk：Key的维度，用于缩放防止梯度爆炸
注意力机制的本质是：通过Q与K的相似性，决定对每个V赋予多大的权重，从而实现“有选择地关注”。

在传统Transformer的自注意力机制中，输入序列中的每个位置（每个词/子词对应的嵌入向量）都会生成自己独立的查询（Query, q）、键（Key, k）和值（Value, v）向量。这是自注意力机制的核心设计之一，但是每个输入位置（token）都生成独立的 q、k、v 向量，也是 Transformer 架构中计算和内存消耗的主要来源之一。每个 token 的嵌入向量（d_model 维）需通过三个独立的线性变换，权重矩阵 W_q, W_k, W_v，每个维度 d_model × d_model。

在大模型注意力机制中，在传统查询 Q 是基础上，为了增强注意力能力与模型表达与优化计算量、显存消耗衍生出了 MHA、MQA、GQA 等多种注意力机制。

传统查询 Q：在注意力机制中，传统查询 Q 是用于表示当前 token 对其他 token 关注度的向量。通过将输入序列经过线性变换得到 Q，再与键向量 K 进行点积运算，得到注意力分数，进而与值向量 V 加权求和，得到最终的注意力输出，以此来确定当前 token 与其他 token 的相关程度，聚焦关键信息。

多头注意力机制（MHA）中的查询：MHA 是 Transformer 架构的核心组件。它将输入向量分别通过多个线性变换层，得到多个查询 Q、键 K 和值 V 矩阵，每个头都有独立的 Q、K、V。然后每个头分别进行注意力计算，最后将结果拼接并经过线性变换得到最终输出。这种方式允许不同的查询头关注不同的 Key - Value 信息，提高了模型的表达能力，适合复杂任务，但推理速度慢，KV 缓存大，占用大量显存和内存带宽。在Transformer架构中，注意力机制几乎总是采用多头注意力（Multi-Head Attention），而非单头。单头注意力只能从一种“视角”捕捉序列中的依赖关系（如仅关注语法结构或局部语义），无法同时建模多种复杂关系。

多查询注意力机制（MQA）中的查询：MQA 是 MHA 的变体，其让所有的头之间共享同一份 Key 和 Value 矩阵，每个头只单独保留一份 Query 参数。相比 MHA，MQA 大大减少了 Key 和 Value 矩阵的参数量，提升了推理速度，显存占用低，适用于大规模语言模型推理。但由于所有头共享相同的 K、V，不同 Query 头会关注相同的信息，导致模型表达能力下降，可能出现训练不稳定的情况。

分组查询注意力机制（GQA）中的查询：GQA 也是 MHA 的变体，它将查询头分成 G 组，每个组内的头共享一个 Key 和 Value 矩阵，而每个头仍单独保留一份 Query 参数。GQA 介于 MHA 和 MQA 之间，部分 Query 头共享 Key - Value，保持了一定的多样性，推理速度比 MHA 快，模型质量比 MQA 高，在推理速度和模型质量之间取得了更好的平衡。
以GQA举例：64个头，将查询头（Query Heads）分为8组。同一组内的所有Query头共享同一组Key和Value。64个Query头 → 8组 → 每组8个头共享1组KV → 最终仅需8组KV（而非64组）。

二、新的注意力机制模型Qwen3-Next-80B-A3B：
阿里发布了新的高效模型使用了混合注意力机制，了解下发现他的注意力机制很不同。模型混合了两种注意力机制，一个标准注意力机制，即前述的传统注意力机制优化版，与另一个改良的标准线性注意力。

标准 Transformer 的自注意力机制计算复杂度与序列长度的平方 (O(L²)) 成正比，这使其在处理长文本时变得异常昂贵。线性注意力的核心思想是通过改变计算顺序，将复杂度降低到线性级别 (O(L))。 Attention(Q, K, V) = Softmax(QK^T)V 的核心是计算注意力矩阵 A = Softmax(QK^T)。这个 A 是一个 L x L 的矩阵 (L是序列长度)，矩阵中的每个元素 A_ij 代表第 i 个查询（Query）对第 j 个键（Key）的关注度。正是这个 L x L 矩阵的计算和存储，导致了 O(L²) 的复杂度。
线性注意力的核心思想是，找到一个函数 sim(Q, K) 来替代 Softmax(QK^T)，并且这个函数满足可分解的性质.也就是说， sim(Q, K) 可以被写作 φ(Q) * φ(K)^T 的形式，其中 φ 是一个应用到 Q 和 K 上的核函数（或称为特征映射）。
那么注意力的计算就可以变成：
Attention(Q, K, V) = (φ(Q) * φ(K)^T) * V
使用结合律Attention(Q, K, V) = φ(Q) * (φ(K)^T * V)
选择合适的核函数 φ 至关重要，它需要很好地近似 Softmax 的效果。一个简单而有效的选择是：
φ(x) = ELU(x) + 1
这里的 ELU 是一个激活函数。使用这个函数可以保证映射后的值都是正数，这在一定程度上模拟了 Softmax 中 exp() 函数的作用，即确保相似度得分是非负的。
线性注意力通过使用一个核函数 φ 来替代标准注意力中的 Softmax 函数，将相似度计算 Softmax(QK^T) 变换为 φ(Q)φ(K)^T 的形式。正是因为这种变换，我们才得以应用矩阵乘法的结合律，将计算顺序重排为 φ(Q) * (φ(K)^T * V)，从而将计算复杂度从 O(L²) 降低到 O(L)。

怎么变成的O(L)?
当前虽然使用了两个 φ 来替代标准注意力中的 Softmax 函数，但是如果仍然(φ(Q) * φ(K)^T) * V依然出现了Q*K^T的计算影子。
若序列长度 (Length) L = 4096
特征维度 (Dimension) d = 64
输入矩阵维度:
Q (查询): L x d (4096 x 64)
K (键): L x d (4096 x 64)
V (值): L x d (4096 x 64)
K^T (K的转置) 的维度是 d x L (64 x 4096)。
计算 A = Q * K^T，结果矩阵 A 的维度是 (L x d) * (d x L) = L x L (4096 x 4096)。
通过结合律改成φ(Q) * (φ(K)^T * V)的计算会变成：
先计算 S = K^T * V:
K^T 的维度是 d x L (64 x 4096)。
V 的维度是 L x d (4096 x 64)。
计算结果 S 的维度是 (d x L) * (L x d) = d x d (64 x 64)。
得到了一个大小为 d x d 的小矩阵。
这个矩阵的大小与序列长度 L 无关。
计算它的复杂度是 d * L * d = O(Ld²)，这是一个线性复杂度。

变化计算顺序后S = K^T * V 可以看作是输入内容的状态，因为矩阵乘法的定义是 S_ij = Σ (K^T)_ik * V_kj，注意是K^T的累和。
S = Σ (k_t * v_t^T)，其中 k_t 和 v_t 分别是第 t 个时间步的键向量和值向量。遍历了整个序列（从t=1到L），对于每一个位置 t，它都将该位置的“键”向量 (k_t) 与“值”向量 (v_t) 进行外积运算，然后将所有这些外积结果累加起来。
可以把 V 看作输入模型的内容， K 看作内容序列的索引。K^T * V 这个操作，是获取整个内容的状态值,把所有信息压缩到一起。

三、混合注意力的缺陷与优化：
线性注意力机制是有一个缺陷，它不能很好的兼顾全局特征信息关系。为了处理这个问题，加入了Gated DeltaNet与门控注意力。

Gated DeltaNet 本质上是一种经过精心改良的线性注意力机制。线性注意力利用矩阵乘法的结合律，将计算顺序变为 Q * (K^T * V)。其中 K^T * V 可以被看作一个“记忆”或“状态”，它不断累积序列的信息。但是简单的累积式更新存在一个严重问题，随着序列变长，新的信息不断被加到旧的记忆中，导致关键信息被稀释，模型难以精确地回忆起早期的特定内容。 这就是 DeltaNet 和门控机制要解决的核心痛点。

Delta 规则借鉴了机器学习中的一个经典概念，即根据误差来调整权重。其核心思想是：在添加新信息之前，先减去一个“预估的旧信息”，从而实现对记忆的精确修改，而非简单的叠加。
传统的线性注意力更新记忆的方式可以简化为：
新记忆 = 旧记忆 + 新的键值对信息
而 DeltaNet 的更新方式则是：
新记忆 = 旧记忆 + (新的键值对信息 - 基于旧记忆对新信息的预测)
这里的“预测”可以理解为：用旧的记忆状态去“看待”新来的信息（key），看看能获得哪些内容。如果新信息与旧记忆高度相关，那么预测值就会很大，相减之后实际增加的量就小，避免了信息冗余。反之，如果新信息是全新的、出乎意料的，预测值就会很小，那么这个新信息就会被更完整地保留下来。
通过这种“减法”操作，Delta 规则实现了对记忆的更精确更新，增强了模型进行关联性回忆的能力。

累加的状态数据容量是有限的，当遇到完全不同的上下文内容时，模型需要能够“清空”或“淡化”不再相关的旧记忆。这便把门控机制引入模型，可以动态地控制信息的流动和保留。门控因子通常由输入数据计算得出一个 0 到 1 之间的值，然后用这个值来调节记忆的更新。
工作原理：
结合了门控的更新过程可以简化为：
新记忆 = A * 旧记忆 + B * 新信息
这里的 A 和 B 就是由门控动态计算出来的系数。如果门控判断当前信息与历史关联不大，它可能会给 A 一个很小的值，这就相当于“关小阀门”，让大部分旧记忆“流失”掉，从而为新信息腾出空间。这种快速内存擦除的能力对于处理上下文主题频繁切换的复杂文本至关重要。
Delta 规则 负责如何精确地写入和修改记忆，它提升了信息更新的质量。
门控机制 负责决定何时遗忘以及遗忘多少，它提升了记忆管理的灵活性。
二者结合，形成了一种强大而高效的记忆更新机制——门控 Delta 规则。 它让模型既能通过门控快速丢弃无用信息，又能通过 Delta 规则对需要保留的记忆进行精细化、有针对性的修改。
并且模型实验经验是引入标准注意力，按照线性注意力3:1标准注意力混合使用。其核心目的是为了弥补线性注意力的固有短板，从而实现更强大的全局特征捕获能力。