先进电机拓扑及控制算法介绍(3)——以“数据”驱动电机实现真正的无模型
1. 背景介绍
之前已经介绍过“无模型预测控制(Model-Free Predictive Control/MFPC)”中的“无模型预测电流控制(Model-Free Predictive Current Control/MFPCC)”,可参考下面知乎。
https://zhuanlan.zhihu.com/p/660705382![]() https://zhuanlan.zhihu.com/p/660705382
https://zhuanlan.zhihu.com/p/660705382
但是后来也有说过,这个MFPCC,其实是利用扩张状态观测器(Extended State Observer/ESO)消除了磁链和电阻的影响。电感则是影响了MFPCC的增益,如果增益设置的不恰当,MFPCC依旧会性能不佳,甚至失去稳定。
今年在预测控制大会上听了汪老师的报告,其报告内容就属于下面这篇参考文献。
[1] F. Wang, Y. Wei, J. Rodriguez and C. Garcia, "State-of-Art, Development, and Challenges of Model-Free Predictive Control on Motor Drives," in IEEE Transactions on Power Electronics, vol. 40, no. 8, pp. 10846-10864, Aug. 2025, doi: 10.1109/TPEL.2025.3559514.
论文中有下面一张图,我觉得画的很形象。图中的MBPC为model-based predictive control,即“基于模型的预测控制”。图中的Data-driven就是“adj. 数据驱动的”,关于“数据驱动”,官方化的解释为:数据驱动的概念由全国科学技术名词审定委员会于2008年审定发布,其核心内涵是以数据为核心驱动力,通过数据采集、清洗、建模和分析提取价值信息,支撑高效决策与操作的技术范式。
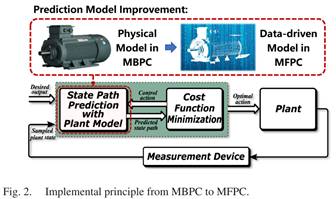
我个人的拙见:“数据驱动”放在电机控制系统而言,相当于根据电机运行得到的电流(包括电流变化量)以及参考电压数据(包括电压变化量),并利用一些算法得到这些之间内在联系,进而拟合出一个“虚构的电机模型”,并根据这个“虚构的电机模型”对电机实行控制。
根据汪老师的报告,我找到了其在24年发表的TIE,以这篇文献为基础来学习一下Data-driven Model in MFPC。
论文链接:https://ieeexplore.ieee.org/document/10505794
[2] Y. Wei, H. Young, D. Ke, F. Wang, H. Qi and J. Rodríguez, "Model-Free Predictive Control Using Sinusoidal Generalized Universal Model for PMSM Drives," in IEEE Transactions on Industrial Electronics, vol. 71, no. 11, pp. 13720-13731, Nov. 2024, doi: 10.1109/TIE.2024.3379667.

文章的摘要:“为了解决模型预测控制(MPC)中参数失配导致的鲁棒性较差的问题,无模型预测控制在电机驱动系统中得到了广泛的应用。该方法用数据驱动模型代替先验模型,消除了物理参数的影响。然而,旋转坐标系对模型精度的影响是多方面的,特别是位置信号不准确和控制器不对称会造成误差。本文提出了一种无模型预测控制策略,利用正弦广义通用模型直接控制正弦信号,并结合历史数据提高了模型精度,反映了被控对象的运动特性。该模型是根据被控对象的信号变化设计的,并使用递推最小二乘(RLS)算法在线估计系数以确保模型的精度。为了在连续控制集(CCS)控制器中实现控制,利用时移和拉格朗日算法设计了预测信号,并根据极点/零点位置和微分方程组分析了预测信号的基本性能和稳定性。将该控制策略作为预测电流控制策略应用于永磁同步电机(PMSM)驱动系统,给出了不同运行条件下的实验结果,验证了该方法的有效性和优越性。”
2. 算法的简单介绍
所提算法的控制框图如下。其采用双闭环控制,外环采用传统的PI控制,速度外环产生的参考电流经过坐标变换后得到阿尔法α,贝塔β电流的参考值。然后内环采用所提的基于“数据驱动”的无模型预测电流控制。
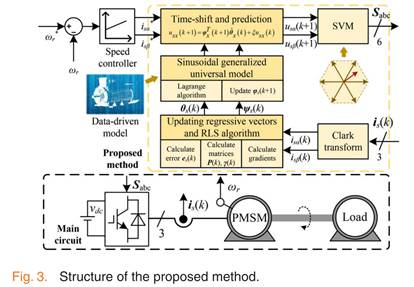
其电流环的算法框图如下:
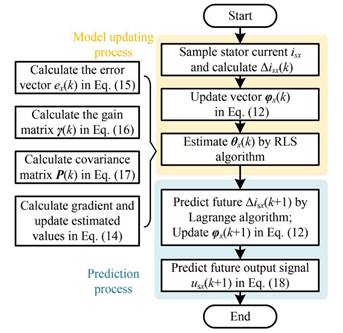
下面我们来详细看看相关公式。首先是式子(9)-(11)。
式子(9)的意思是,电机系统的k+1时刻的电压增量,可以通过往期的n+1组电流增量数据以及m+1组电压增量数据得到(在文中,这个n,m取2或者3即可)。

那接下来的问题就是,这n+1组电流增量数据以及m+1组电压增量数据与k+1时刻的电压增量的关系,到底从何而来?这时候就需要看到式子(12)到式子(18)。
文中中是用“最小二乘法”去拟合n+1组电流增量数据以及m+1组电压增量数据与k+1时刻的电压增量的关系。当然你换别的方法也可以。

这里值得注意的一些问题是,k+1时刻的参考电流到底从何而来?文章说采用拉格朗日算法,但文章没给具体的公式。我是在汪老师的另一篇论文找到了相关公式。公式如下:
[3] F. Wang, Y. Wei, H. Young, D. Ke, D. Huang and J. Rodríguez, "Continuous-Control-Set Model-Free Predictive Control Using Time-Series Subspace for PMSM Drives," in IEEE Transactions on Industrial Electronics, vol. 71, no. 7, pp. 6656-6666, July 2024, doi: 10.1109/TIE.2023.3310017.

我自己在仿真中的话,是利用dq电流的参考电流,经过坐标变换得到k+1时刻的参考电流。
值得注意的是,论文中的(14)-(17)所写出的最小二乘法表达式略有所错误(个别字母/符号标错),需要自己重新推导且去了解其这样设计的含义。这点小差错不影响文章的思路。
该算法是在线运行的,并不是离线驱动。需要电机先跑起来一下,便可以切换到该基于“数据驱动”的无模型预测电流控制。
下面先进行仿真验证,在本文的第三节验证模型数据的数量选择的影响以及反馈系数的影响。第四节进行算法对比。
3.参数影响
仿真参数设置:
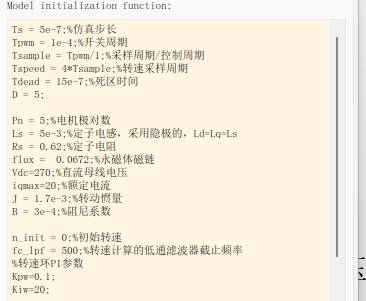
仿真工况设置:
0.4s前,电流环采用传统的电流环控制方式,电机给定转速为2000r/min,负载为8Nm;前0.4s相当于为数据驱动无模型预测电流控制提供必要的“数据”信息。0.4s之后切入数据驱动无模型预测电流控制,并且在0.6s处让电机减速1000r/min,在0.8s减载至5Nm,以验证电机的动态性能。
3.1 数据量选择的影响
文中说需要n+1组电流增量数据以及m+1组电压增量数据去计算k+1时刻的电压增量。文中说,n和m取2或者3即可。
在汪老师的另一篇文献中做了自适应的阶数选择,其实验结果也是在2、3之间波动。
[4] Y. Wei, H. Young, D. Ke, D. Huang, F. Wang and J. Rodríguez, "Adaptive Ultralocalized Time-Series for Improved Model-Free Predictive Current Control on PMSM Drives," in IEEE Transactions on Power Electronics, vol. 39, no. 5, pp. 5155-5165, May 2024, doi: 10.1109/TPEL.2024.3357854.
3.1.1 n = m = 2的仿真波形
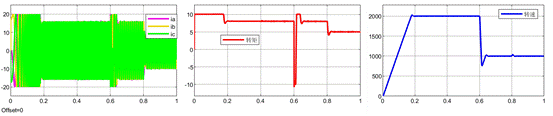
n = m = 2,即采用3组电流增量数据以及3组电压增量数据去拟合k+1时刻的电压,仿真的整体波形如下。
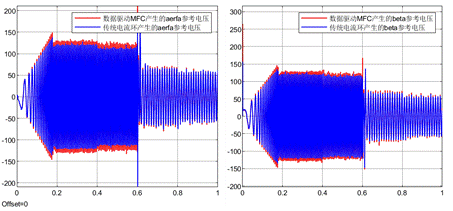
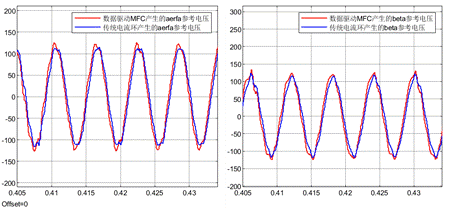
下面是传统电流环和数据驱动无模型预测电流控制产生的阿尔法贝塔参考电压的对比。从下面的波形可以看到,两种算法产生的参考电压差不多,有一定偏差。两种算法产生的参考电压差不多说明二者性能也将差不多。
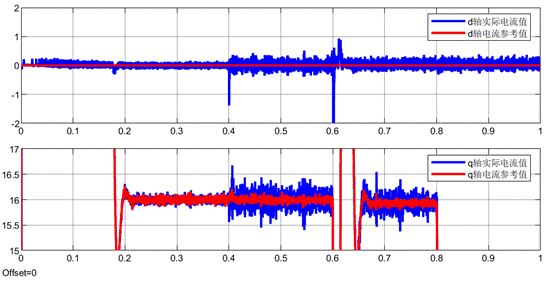
下面放大dq电流波形,可以看到,其实在0.4s切换到数据驱动无模型预测电流控制,是会出现更大的电流波动。但是考虑到该算法毕竟不需要任何的电机参数,其还是有明显的价值的。
3.1.2 n = m = 3的仿真波形
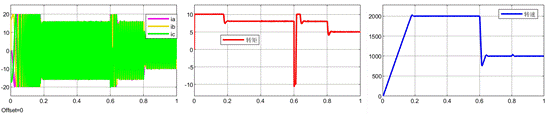
n = m = 3,即采用4组电流增量数据以及4组电压增量数据去拟合k+1时刻的电压,仿真的整体波形如下。
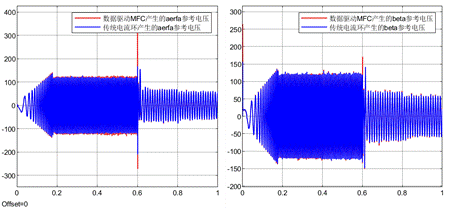
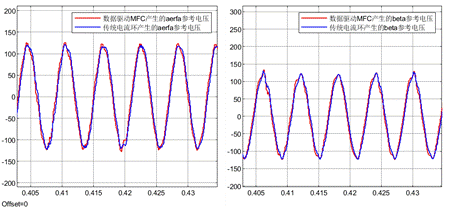
下面是传统电流环和数据驱动无模型预测电流控制产生的阿尔法贝塔参考电压的对比。从下面的波形可以看到,两种算法产生的参考电压基本一致,这说明:
(1)对该仿真条件而言,相比于3组电流增量数据以及3组电压增量数据(n = m = 2),采用4组电流增量数据以及4组电压增量数据(n = m = 3)能够实现更好的拟合拟合效果。
(2)该数据驱动无模型预测电流控制可以在不需要任何电机参数的条件下就可以实现与传统算法基本一致的性能。
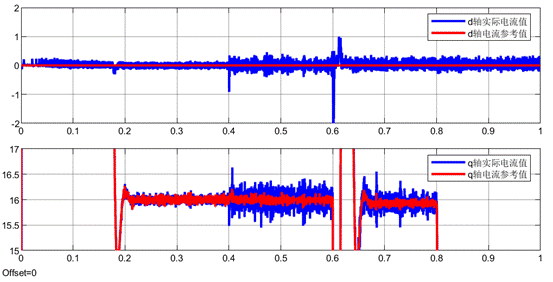
下面放大dq电流波形,可以看到,其实在0.4s切换到数据驱动无模型预测电流控制,是会出现更大的电流波动。但是考虑到该算法毕竟不需要任何的电机参数,其还是有明显的价值的。
3.2 反馈增益的影响
论文中的控制律涉及到一个反馈系数。

从图12的实验结果可以看到,当反馈系数在0.90到1之间时,总的来说,电流THD会随着反馈系数的提高而增加。
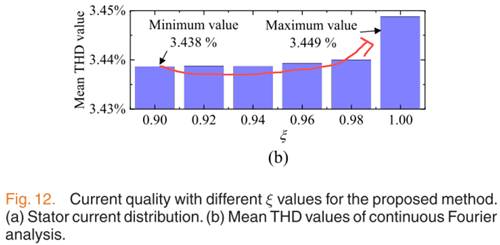
下面就进行了不同反馈系数的仿真对比,反馈系数分别取0.9和1.0。从下面仿真可以看到,反馈系数为0.9时的相电流THD(1.16%)确实会略低于反馈系数为1时的相电流THD(1.32%),这与实验的情况基本一致。
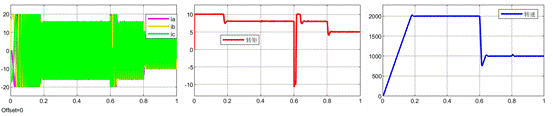
反馈系数为0.9的整体波形
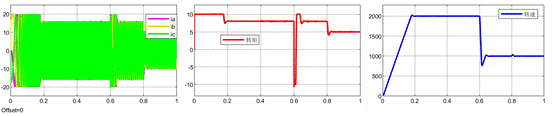
反馈系数为1的整体波形
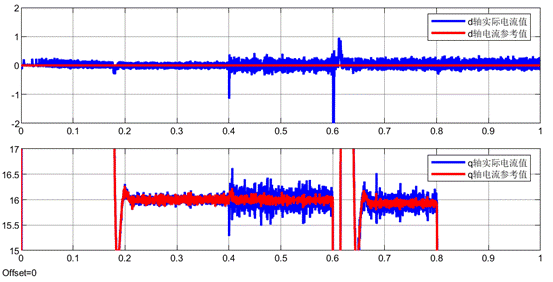
反馈系数为0.9的dq电流波形
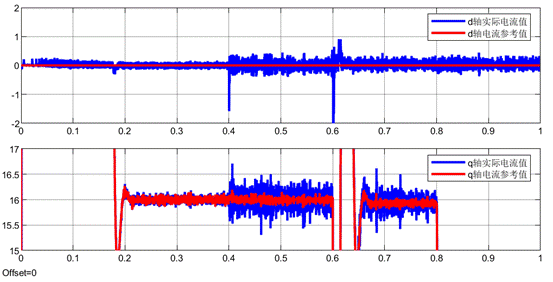
反馈系数为1的dq电流波形
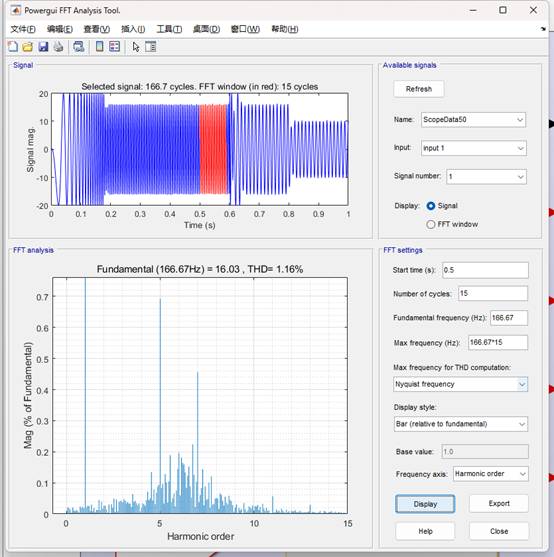
反馈系数为0.9的相电流FFT分析
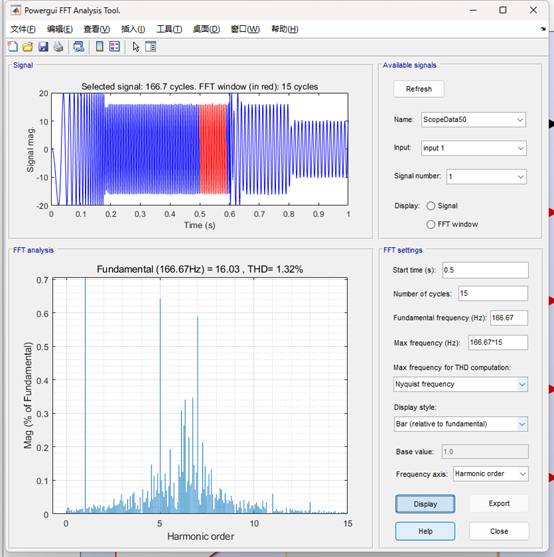
反馈系数为1的相电流FFT分析
4. 仿真对比
下面进行三组仿真的对比:
1. 基于LESO的MFPCC(LESO的带宽取为4000,控制器中的电感参数设置为实际电感参数)
2. 基于数据驱动的MFPCC(n=m=3,反馈系数取0.9)
3. 基于LESO的MFPCC(LESO的带宽取为4000,控制器中的电感参数设置为实际电感参数的2倍,以模拟参数失配)
PS:对于基于数据驱动的MFPCC,在0.3s前,由基于LESO的MFPCC驱动电机,以其数据作为基于数据驱动的MFPCC的支撑。0.3s后切入基于数据驱动的MFPCC。
4.1 整体波形的对比
下面是整体波形的对比。从下面仿真可以得到以下结论。
(1)对于基于LESO的MFPCC,在控制器中的电感参数设置为实际电感参数时,其控制效果极佳;
(2)但当控制器中的电感参数设置为实际电感参数的2倍时,系统开始引入大量高频噪声;
(3)相对基于LESO的MFPCC(控制器中的电感参数设置为实际电感参数),基于数据驱动的MFPCC的转矩脉动有所增加。
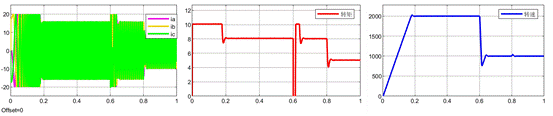
基于LESO的MFPCC(控制器中的电感参数设置为实际电感参数)
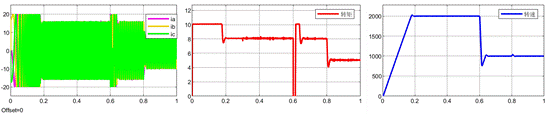
基于数据驱动的MFPCC
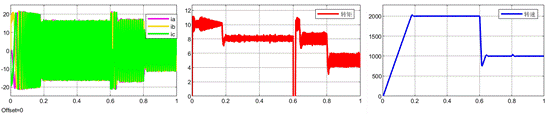
基于LESO的MFPCC(控制器中的电感参数设置为实际电感参数的2倍)
4.2 相电流FFT的对比
(1)基于LESO的MFPCC(控制器中的电感参数设置为实际电感参数)的电流THD为0.55%;
(2)基于数据驱动的MFPCC的电流THD为1.13%
(3)基于LESO的MFPCC(控制器中的电感参数设置为实际电感参数的2倍)的电流THD为4.19%。
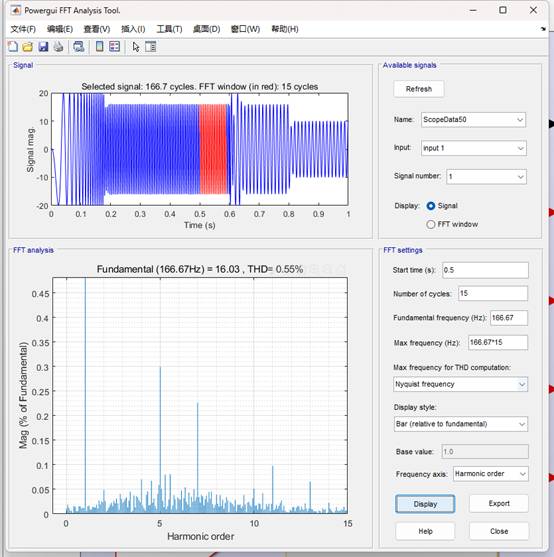
基于LESO的MFPCC(控制器中的电感参数设置为实际电感参数)
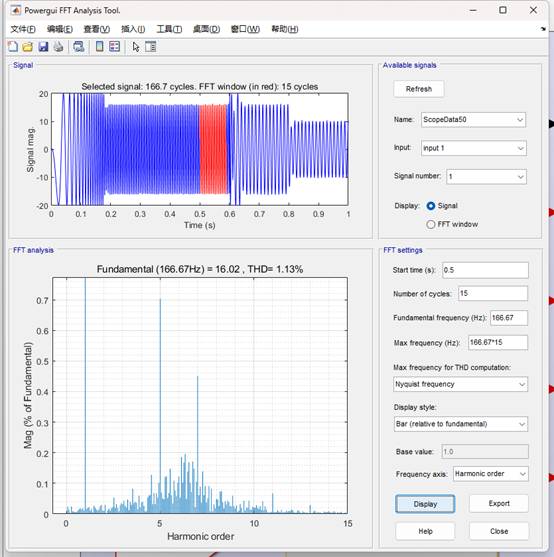
基于数据驱动的MFPCC
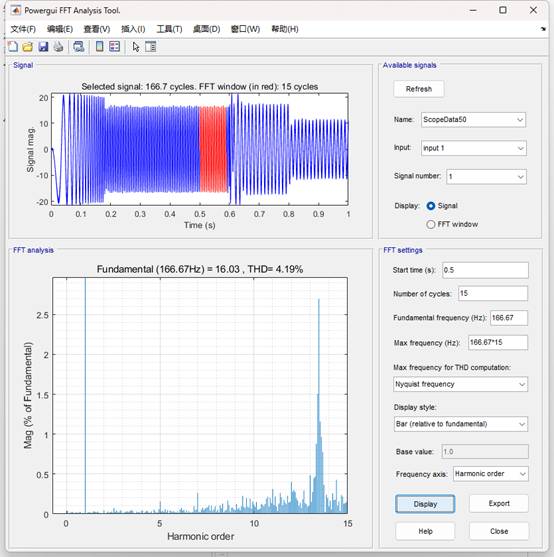
基于LESO的MFPCC(控制器中的电感参数设置为实际电感参数的2倍)
4.3 变速条件下电流的跟踪情况
在0.6s的时候设置了电机减速,所以q轴电流的参考值会直接达到负的最大值(-20A)。从大体上来看,基于LESO的MFPCC(控制器中的电感参数设置为实际电感参数)和基于数据驱动的MFPCC的电流跟踪情况非常接近。
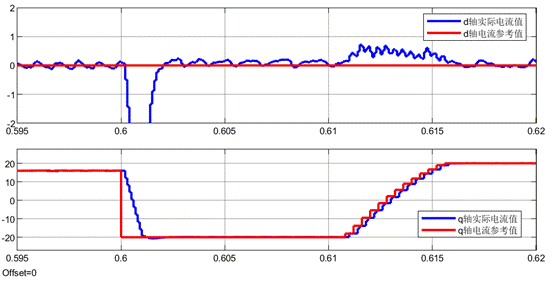
基于LESO的MFPCC(控制器中的电感参数设置为实际电感参数)
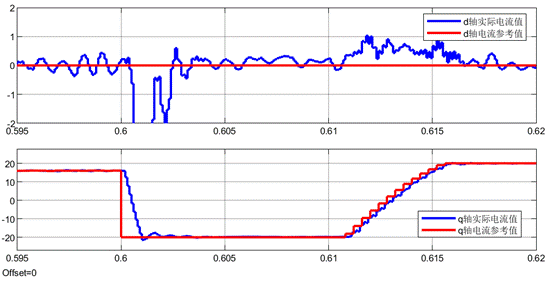
基于数据驱动的MFPCC
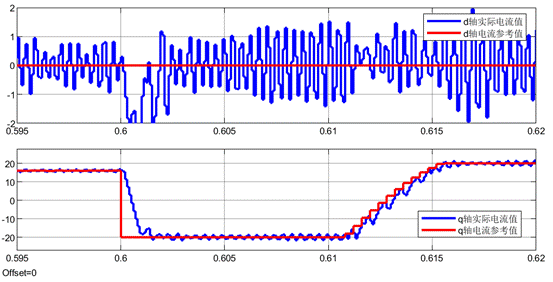
基于LESO的MFPCC(控制器中的电感参数设置为实际电感参数的2倍)
5.总结与思考
总结
本篇文章学习并复现了一篇基于数据驱动的MFPCC,该方法仅需要极短时间的数据即可构建出电机模型,并且以此模型进行闭环控制。该算法不需要任何电机参数即可实现较为优异的控制性能(THD略高于无参数失配条件下的LESO-MPFCC且动态性能基本一致),个人认为这样性能还是比较优异的。
思考
在电机控制领域,相关算法感觉才处于刚起步的阶段。这篇文章,我认为在个方面说的都比较详细了,其实仔细看文章内容并去思考,会发现还有许多可以完善的地方。
虽然在仿真中,这基于数据驱动的MFPCC略微弱于无参数失配条件下的LESO-MPFCC,但是如果换个角度去看,比如说遇到一个多相的、磁场较为复杂的电机,其数学模型是较为复杂。如果人为的去建模,很可能无法构建精确的模型,也就无法人为的设计出性能较为优异的控制算法。这时候的基于数据驱动的MFPCC是否会更好呢?
