当前位置：首页 > news >正文

Scikit-learn 对加州房价数据集（回归任务）进行全面分析

news 2025/9/14 7:29:47

背景

加利福尼亚房价数据集 fetch_california_housing，20640个样本，8个特征（人口、收入等），目标为房价中位数
该数据集是一个回归问题，需要运用回归任务的分析方法进行分析

分析方法

线性回归
K 近邻（K-NN）
决策树
支持向量机
随机森林
多层感知机（MLP）
Lasso 回归
Ridge 回归
梯度提升回归
AdaBoost 回归
Huber 回归

分析步骤

加载数据集
拆分训练集、测试集
数据预处理（标准化）
选择模型
模型训练（拟合）
测试模型效果
评估模型

分析结果

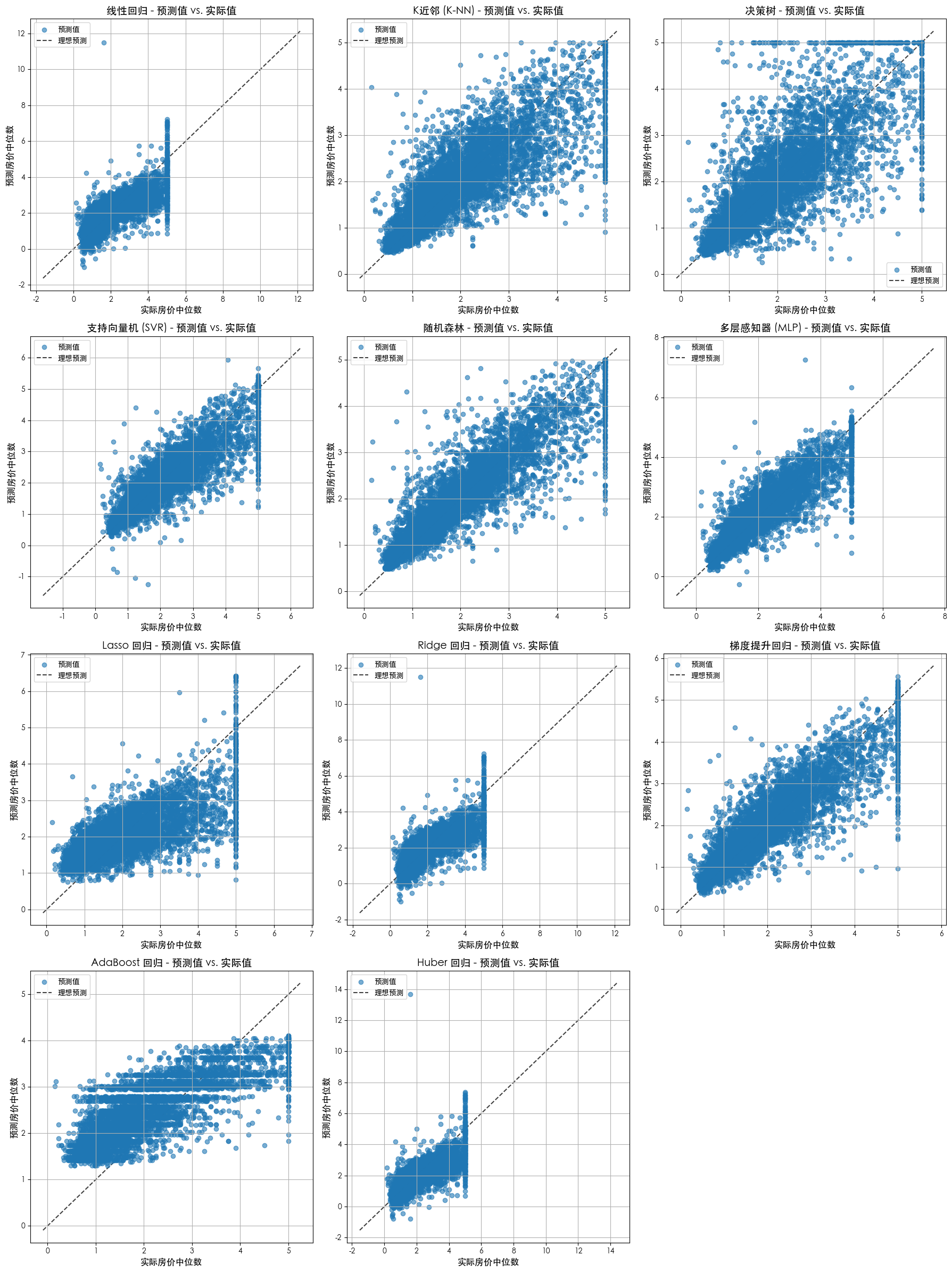
不同模型的预测值 vs 真实值

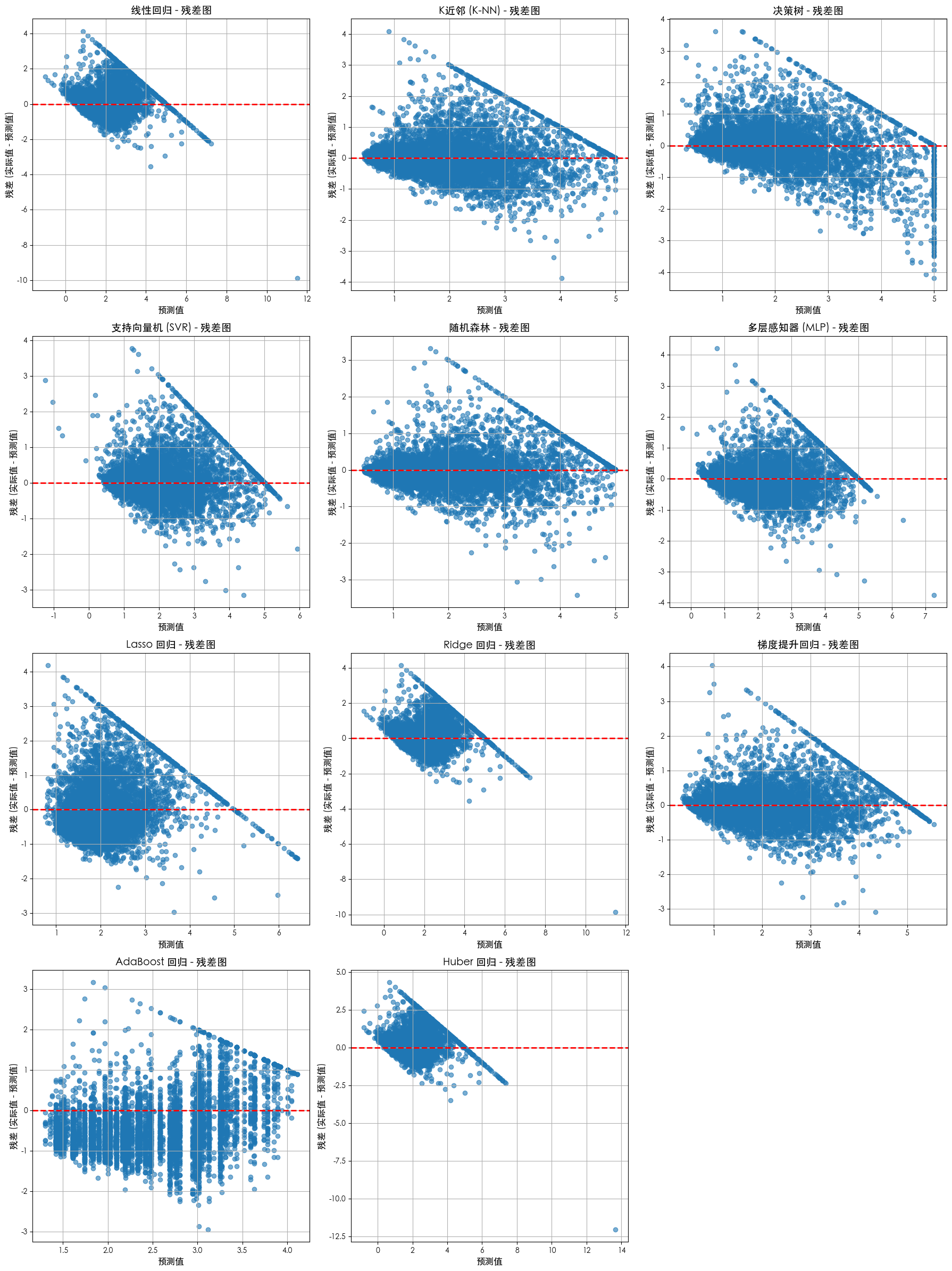
残差图

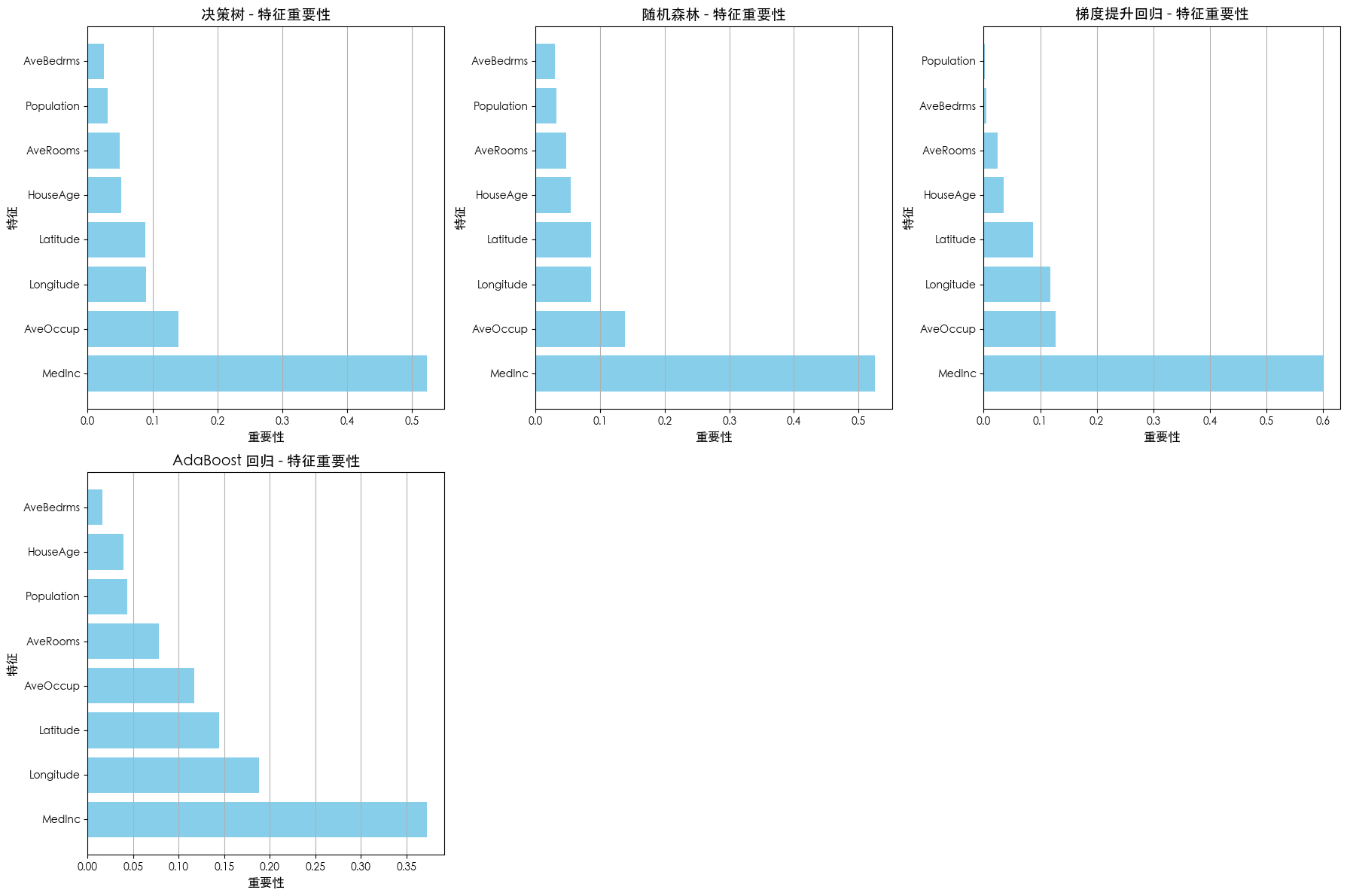
特征重要性对比

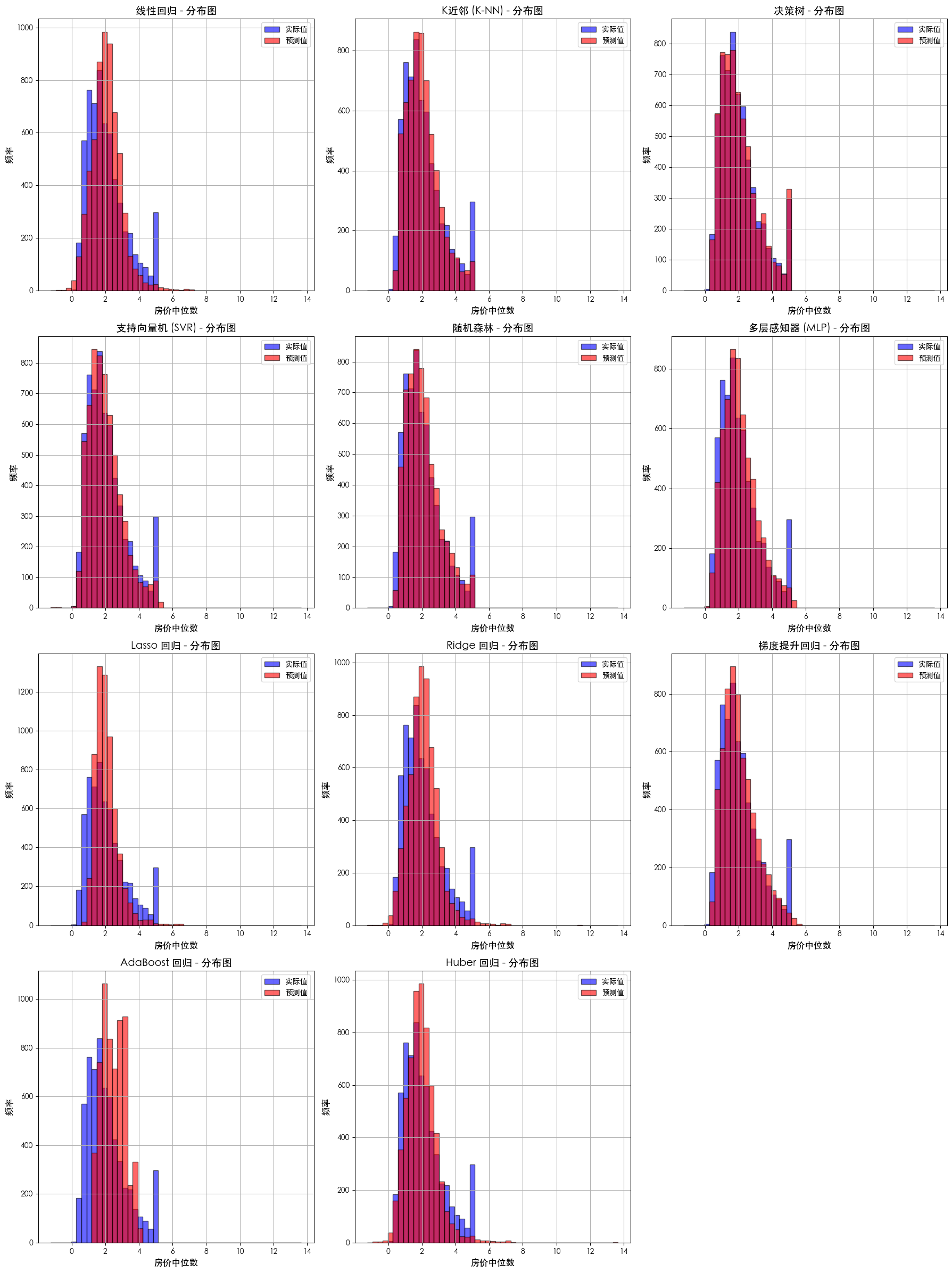
预测值分布

不同模型评估明细

--- 正在加载加州房价数据集 ------ 数据集概览 ---
数据形状: (20640, 8)
特征名称: ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude']
目标变量名称: MedHouseVal--- 数据划分结果 ---
训练集形状: (14448, 8)
测试集形状: (6192, 8)--- 正在对数据进行标准化处理 ------ 模型训练与评估 ------ 正在训练 线性回归 模型 ---
线性回归 模型的均方误差 (MSE): 0.5306
线性回归 模型的 R^2 得分: 0.5958--- 正在训练 K近邻 (K-NN) 模型 ---
K近邻 (K-NN) 模型的均方误差 (MSE): 0.4295
K近邻 (K-NN) 模型的 R^2 得分: 0.6728--- 正在训练 决策树 模型 ---
决策树 模型的均方误差 (MSE): 0.5250
决策树 模型的 R^2 得分: 0.6000--- 正在训练 支持向量机 (SVR) 模型 ---
支持向量机 (SVR) 模型的均方误差 (MSE): 0.3099
支持向量机 (SVR) 模型的 R^2 得分: 0.7639--- 正在训练 随机森林 模型 ---
随机森林 模型的均方误差 (MSE): 0.2573
随机森林 模型的 R^2 得分: 0.8040--- 正在训练 多层感知器 (MLP) 模型 ---
多层感知器 (MLP) 模型的均方误差 (MSE): 0.2897
多层感知器 (MLP) 模型的 R^2 得分: 0.7793--- 正在训练 Lasso 回归 模型 ---
Lasso 回归 模型的均方误差 (MSE): 0.6648
Lasso 回归 模型的 R^2 得分: 0.4935--- 正在训练 Ridge 回归 模型 ---
Ridge 回归 模型的均方误差 (MSE): 0.5305
Ridge 回归 模型的 R^2 得分: 0.5958--- 正在训练 梯度提升回归 模型 ---
梯度提升回归 模型的均方误差 (MSE): 0.2883
梯度提升回归 模型的 R^2 得分: 0.7803--- 正在训练 AdaBoost 回归 模型 ---
AdaBoost 回归 模型的均方误差 (MSE): 0.6830
AdaBoost 回归 模型的 R^2 得分: 0.4797--- 正在训练 Huber 回归 模型 ---
Huber 回归 模型的均方误差 (MSE): 0.5515
Huber 回归 模型的 R^2 得分: 0.5798所有模型的分析已完成。

代码

注：如果遇到下载数据集失败（HTTP 403），可参考此博文 https://blog.csdn.net/xchenhao/article/details/151373379

from sklearn.datasets import fetch_california_housingfrom sklearn.model_selection import train_test_splitfrom sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.svm import SVR
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.linear_model import Lasso, Ridge
from sklearn.ensemble import GradientBoostingRegressor, AdaBoostRegressor
from sklearn.linear_model import HuberRegressorfrom sklearn.metrics import mean_squared_error, r2_scoreimport numpy as np
import matplotlib.pyplot as plt# 设置 Matplotlib 字体以正确显示中文
plt.rcParams['font.sans-serif'] = ['SimHei', 'WenQuanYi Zen Hei', 'STHeiti', 'Arial Unicode MS']
# 解决保存图像时负号'-'显示为方块的问题
plt.rcParams['axes.unicode_minus'] = False def perform_housing_analysis():"""使用 scikit-learn 对加州房价数据集进行全面的分析。该函数包含数据加载、预处理、模型训练、评估和结果可视化。"""print("--- 正在加载加州房价数据集 ---")# 加载加州房价数据集housing = fetch_california_housing(as_frame=True)# 获取数据特征和目标标签X = housing.datay = housing.targetfeature_names = list(X.columns)print("\n--- 数据集概览 ---")print(f"数据形状: {X.shape}")print(f"特征名称: {feature_names}")print(f"目标变量名称: {housing.target.name}")# 将数据集划分为训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)print("\n--- 数据划分结果 ---")print(f"训练集形状: {X_train.shape}")print(f"测试集形状: {X_test.shape}")# 数据标准化print("\n--- 正在对数据进行标准化处理 ---")scaler = StandardScaler()X_train_scaled = scaler.fit_transform(X_train)X_test_scaled = scaler.transform(X_test)# 定义并训练多个回归器模型models = {"线性回归": LinearRegression(),"K近邻 (K-NN)": KNeighborsRegressor(n_neighbors=5),"决策树": DecisionTreeRegressor(random_state=42),"支持向量机 (SVR)": SVR(kernel='rbf', C=100),"随机森林": RandomForestRegressor(random_state=42),"多层感知器 (MLP)": MLPRegressor(random_state=42, max_iter=10000),"Lasso 回归": Lasso(alpha=0.1, max_iter=10000),"Ridge 回归": Ridge(alpha=1.0, max_iter=10000),"梯度提升回归": GradientBoostingRegressor(random_state=42),"AdaBoost 回归": AdaBoostRegressor(random_state=42),"Huber 回归": HuberRegressor(max_iter=10000)}# 用于存储所有模型的预测结果predictions = {}# 用于存储树模型的特征重要性feature_importances = {}print("\n--- 模型训练与评估 ---")for name, model in models.items():print(f"\n--- 正在训练 {name} 模型 ---")model.fit(X_train_scaled, y_train)y_pred = model.predict(X_test_scaled)# 计算回归指标mse = mean_squared_error(y_test, y_pred)r2 = r2_score(y_test, y_pred)print(f"{name} 模型的均方误差 (MSE): {mse:.4f}")print(f"{name} 模型的 R^2 得分: {r2:.4f}")# 存储预测结果以用于后续可视化predictions[name] = y_pred# 检查模型是否具有特征重要性属性if hasattr(model, 'feature_importances_'):feature_importances[name] = model.feature_importances_print("\n所有模型的分析已完成。")# --- 预测值 vs. 实际值可视化 ---print("\n--- 预测值 vs. 实际值散点图 ---")num_models = len(models)cols = 3rows = (num_models + cols - 1) // colsfig, axes = plt.subplots(rows, cols, figsize=(18, 6 * rows))axes = axes.flatten()for i, name in enumerate(models.keys()):ax = axes[i]y_pred = predictions[name]ax.scatter(y_test, y_pred, alpha=0.6, label='预测值')lims = [np.min([ax.get_xlim(), ax.get_ylim()]),np.max([ax.get_xlim(), ax.get_ylim()]),]ax.plot(lims, lims, 'k--', alpha=0.75, zorder=0, label='理想预测')ax.set_title(f'{name} - 预测值 vs. 实际值', fontsize=14)ax.set_xlabel('实际房价中位数', fontsize=12)ax.set_ylabel('预测房价中位数', fontsize=12)ax.legend()ax.grid(True)for j in range(num_models, len(axes)):axes[j].axis('off')plt.tight_layout()plt.show()# --- 残差图可视化 ---print("\n--- 残差图可视化 ---")fig, axes = plt.subplots(rows, cols, figsize=(18, 6 * rows))axes = axes.flatten()for i, name in enumerate(models.keys()):ax = axes[i]y_pred = predictions[name]# 计算残差 (实际值 - 预测值)residuals = y_test - y_predax.scatter(y_pred, residuals, alpha=0.6)ax.axhline(y=0, color='r', linestyle='--', linewidth=2)ax.set_title(f'{name} - 残差图', fontsize=14)ax.set_xlabel('预测值', fontsize=12)ax.set_ylabel('残差 (实际值 - 预测值)', fontsize=12)ax.grid(True)for j in range(num_models, len(axes)):axes[j].axis('off')plt.tight_layout()plt.show()# --- 特征重要性可视化 (仅限树模型) ---if feature_importances:print("\n--- 特征重要性可视化 ---")num_tree_models = len(feature_importances)rows_tree = (num_tree_models + cols - 1) // colsfig, axes = plt.subplots(rows_tree, cols, figsize=(18, 6 * rows_tree))axes = axes.flatten()for i, (name, importances) in enumerate(feature_importances.items()):ax = axes[i]# 根据重要性降序排序sorted_indices = np.argsort(importances)[::-1]sorted_importances = importances[sorted_indices]sorted_feature_names = [feature_names[j] for j in sorted_indices]ax.barh(sorted_feature_names, sorted_importances, color='skyblue')ax.set_title(f'{name} - 特征重要性', fontsize=14)ax.set_xlabel('重要性', fontsize=12)ax.set_ylabel('特征', fontsize=12)ax.grid(axis='x')for j in range(num_tree_models, len(axes)):axes[j].axis('off')plt.tight_layout()plt.show()# --- 预测值分布图可视化 ---print("\n--- 预测值分布图 ---")fig, axes = plt.subplots(rows, cols, figsize=(18, 6 * rows))axes = axes.flatten()# 找到所有预测值和实际值的全局范围，以便所有子图的X轴一致all_values = np.concatenate([y_test] + list(predictions.values()))bins = np.linspace(min(all_values), max(all_values), 50)for i, name in enumerate(models.keys()):ax = axes[i]y_pred = predictions[name]# 绘制实际值和预测值的直方图ax.hist(y_test, bins=bins, alpha=0.6, label='实际值', color='b', edgecolor='k')ax.hist(y_pred, bins=bins, alpha=0.6, label='预测值', color='r', edgecolor='k')ax.set_title(f'{name} - 分布图', fontsize=14)ax.set_xlabel('房价中位数', fontsize=12)ax.set_ylabel('频率', fontsize=12)ax.legend()ax.grid(True)for j in range(num_models, len(axes)):axes[j].axis('off')plt.tight_layout()plt.show()if __name__ == "__main__":perform_housing_analysis()