当前位置：首页 > news >正文

深度神经网络1——梯度问题+标签数不够问题

news 2025/9/14 7:06:37

要解决一个复杂问题，可能要训练更深的神经网络，可能会10层及以上，每层包含数百个神经元，成千上万个连接。这样大的神经网络在训练的时候可能会遇到以下问题：
这样在进行反向传播的时候，随着层数越来越低会遇到梯度越来越小或梯度越来越大的情况。
可能没有足够的训练数据或做标签的成本太高
训练速度可能会非常缓慢
固有数百万个参数的模型会有很高的风险过拟合训练集，尤其是在没有足够的训练实例或噪声太大的情况下

一、反向传播——梯度消失和梯度爆炸

梯度消失：如果梯度通常小于1，多次连乘之后梯度会呈指数级缩小，趋近于0。导致底层神经网络的权重更新非常缓慢甚至停止更新。

梯度爆炸：如果梯度通常大于1，多次连乘之后梯度会呈指数级增长，变得非常大。这就导致权重更新步长过大，模型无法收敛。

总结来说，深度神经网受梯度不稳定的影响，不曾的层以不同的速度进行学习。

1、权重初始化

（1）理论

针对这一问题，有学者提出：前向传播的收让每层的输入和输出的方差相等，反向传播时让梯度在同一层的输入和输出具有相同的方差。但是，如果某一层没有相同的数量的输入和输出，这个输入和输出的方差保持一致就不可能实现。因此诞生一个这种的方法Xavier初始化（或者Glorot初始化）

学者指出：对于一个线性层，权重的理想方差应该是 $\frac{2}{n_{in}+n_{out}}$ （ $n_{in}$ 是输入到这个线性层的单元数量， $n_{out}$ 是这个线性层的输出单元数量）。而针对激活函数不同，学者提供类似但有差异的权重初始化方差，如下：

初始化方法	在keras中的参数	激活函数	$\sigma ^2$ 方差
Xavier初始化 Glorot初始化	glorot_normal glorot_uniform	None、tanh、sigmoid、softmax	$\frac{1}{n_{in}+n_{out}}$
He 初始化	he_normal 正态，更自然 he_uniform 均匀，更安全	ReLU、Leaky ReLU 、ELU、GELU、Swish、Mish	$\frac{2}{n_{in}+n_{out}}$ in和out的数量一样
LeCun初始化	lecun_normal	SELU	$\frac{1}{n_{in}+n_{out}}$ in和out的数量一样

初始化方法

在keras中的参数

激活函数

$\sigma ^2$ 方差

Xavier初始化

Glorot初始化

glorot_normal

glorot_uniform

None、tanh、sigmoid、softmax

$\frac{1}{n_{in}+n_{out}}$

He 初始化

he_normal 正态，更自然

he_uniform 均匀，更安全

ReLU、Leaky ReLU 、ELU、GELU、Swish、Mish

$\frac{2}{n_{in}+n_{out}}$

in和out的数量一样

LeCun初始化

lecun_normal

SELU

$\frac{1}{n_{in}+n_{out}}$

in和out的数量一样

（2）使用方法

默认情况下，Keras使用具有均匀分布的Xavier初始化。创建层时，可以通过设置kernel_initializer = "he_uniform"`或 kernel_initializer = "he_normal"`来将其更改为He初始化。

import tensorflow as tfdense = tf.keras.layers.Dense(50,activation="relu",kernel_initalizer = "he_normal")

也可以使用VarianceScaling初始化器获得表中列出的任何初始化以及更多。例如，如果想用均匀分布并且基于fan_avg（而不是fan_in）进行He初始化，则可以使用下面的代码：

he_avg_init = tf.keras.initializers.VarianceScaling(scale=2., mode="fan_avg",distribution="uniform")
dense = tf.keras.layers.Dense(50, activation="relu", kernel_initializer=he_avg_init)

2、选择合适的激活函数

在2010年的一篇论文中提到：梯度不稳定的问题的部分原因是因为激活函数选择不恰当。激活函数的选择直接决定了导数的行为，是解决梯度消失问题的关键。

在使用ReLU激活函数并不完美，因为他在小于0的部分会直接输出0，这样会导致梯度下降不会在影响它，致使神经元死亡。

之前的激活函数的优缺点：

激活函数	缺点	优点
sigmoid函数	梯度消失：输入值很大或很小的时候导数趋近于0，极易导致梯度消失。非零中心：其输出恒为正，导致梯度更新的时候权重向量的更新方向全部为正或负，出现“之”字路径	平滑易于求导输出范围时(0,1) 能够有直观的解释
Tanh函数	虽然比Sigmoid好，但是在输入和输出很大或很小的时候同样存在梯度消失的问题	是0中心（输出范围是-1~1，解决了Sigmoid函数的非零中心问题）
ReLU函数	一旦输入负，梯度为0，神经元不会在被激活（神经元死亡），相应的权重无法更新。	在正区间导数恒为1，彻底解决了梯度消失问题计算速度快，只需要一个阈值判断

激活函数

缺点

优点

sigmoid函数

梯度消失：输入值很大或很小的时候导数趋近于0，极易导致梯度消失。

非零中心：其输出恒为正，导致梯度更新的时候权重向量的更新方向全部为正或负，出现“之”字路径

平滑易于求导

输出范围时(0,1)

能够有直观的解释

Tanh函数

虽然比Sigmoid好，但是在输入和输出很大或很小的时候同样存在梯度消失的问题

是0中心（输出范围是-1~1，解决了Sigmoid函数的非零中心问题）

ReLU函数

一旦输入负，梯度为0，神经元不会在被激活（神经元死亡），相应的权重无法更新。

在正区间导数恒为1，彻底解决了梯度消失问题

计算速度快，只需要一个阈值判断

使用ReLU及其改进版本（如Leaky ReLU, PReLU, ELU）可以显著缓解梯度消失问题。因为它们的导数是常数（如ReLU正区间的导数为1），在连乘时不会导致梯度缩小。

（1）Leaky ReLU函数和PReLU函数

$LeakyReLU_\alpha (z) = max(\alpha z,z)$ 超参数 $\alpha$ 定义函数的泄露程度：z<0时它是函数的斜率，以确保函数在梯度传递的时候永不死亡（可能会长时间昏迷，但是有机会醒来）。在实际应用的过程中大泄露 $\alpha$ 似乎比小泄露 $\alpha$ 能产生更好的性能。

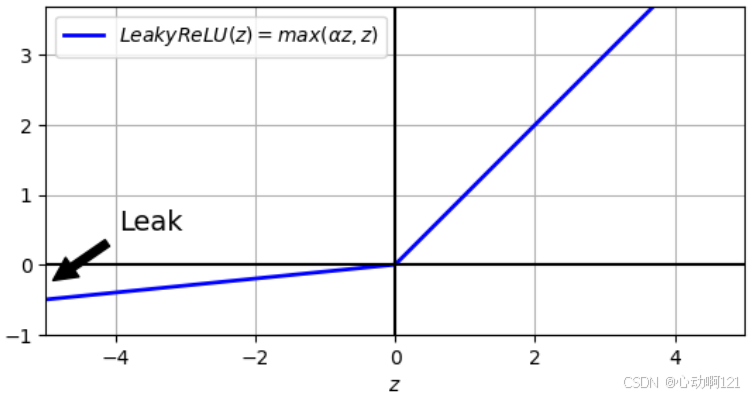
$PReLU_\alpha (z) = max(\alpha z,z)$ ，这函数是LeakyReLU的一个变体，它将 $\alpha$ 参数化，让其变成一个可以在训练期间可以学习的值。

特性	Leaky ReLU (超参数)	PReLU (Parametric ReLU, 可学习参数)
定义	$\text{LeakyReLU}(x) = \max(\alpha x, x)$	$\text{PReLU}(x) = \max(\alpha x, x)$
$\alpha$ 的性质	固定的常数，由人在训练前设定。	模型的一个参数，像权重（Weight）和偏置（Bias）一样，在训练过程中通过反向传播和梯度下降进行优化。
是否更新	否。一旦设定，在整个训练过程中保持不变。	是。它的值会随着训练迭代而自动调整。
如何设定	人工手动设置或通过超参数搜索（如网格搜索）确定。核心目的是给负输入一个非零但很小的梯度，防止神经元“死亡”。因此，它的值应该是一个很小的正数，通常在 `(0, 1)` 范围内	只需要给它一个初始值，然后交给优化器。
例子	`alpha=0.01` (这是最经典、最常用的值) 如果效果不好，在 `[0.3, 0.1, 0.01, 0.001]`	`alpha` 初始化为 `0.25`，训练后可能变为 `0.1`, `0.15`, `0.3` 等。
keras使用	activation="leaky_relu" activation=tf.keras.layers.LeakyReLU()	activation=tf.keras.layers.PReLU()

（2）ELU和SELU

ReLU，leaky ReLU都有不是光滑函数的缺点：它们的导数会突然变化，这种不连续性会使梯度下降在最优值附近反弹，并减慢收敛速度。所以，关注ReLU激活函数的一些平滑变体：ELU和SELU

指数线性单元ELU：

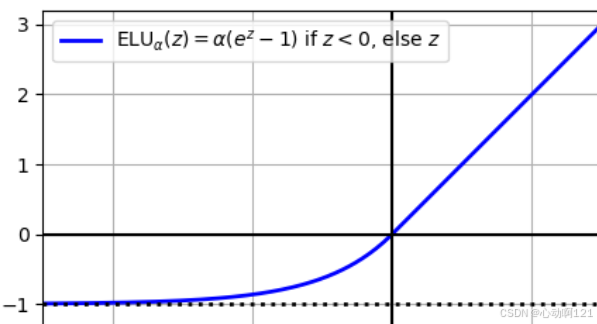
$ELU_\alpha (x) = \begin{cases} \alpha (e^x-1) ,& x<0 \\x, & x \geqslant 0 \end{cases}$

这个函数和之前函数的主要区别：

在负区间ELU不是绝对的零值，而是一个平滑的负饱和值（趋于 $-\alpha$ ）。这意味着即使输入负值，神经元仍有输出，梯度也不为0（ $\text{ELU}'(x<0) = \text{ELU}(x) + \alpha$ ），从而保持了权重更新的可能性，有效缓解了神经元死亡的问题。

相比于之前PReLU和LeakyReLU在负区间时简单的斜线，ELU的负区间是指数曲线，更加平滑，有助于加速梯度下降。

ELU在负区间会产生负的输出，有助于使激活的均值更接近0，有助缓解梯度消失问题。当输入的是一个很大的负数的时候，ELU函数的输出值无限逼近 $-\alpha$ 。这个 $\alpha$ 通常设置为1，能够有很好的收敛效果。

缩放指数线性单元SELU：

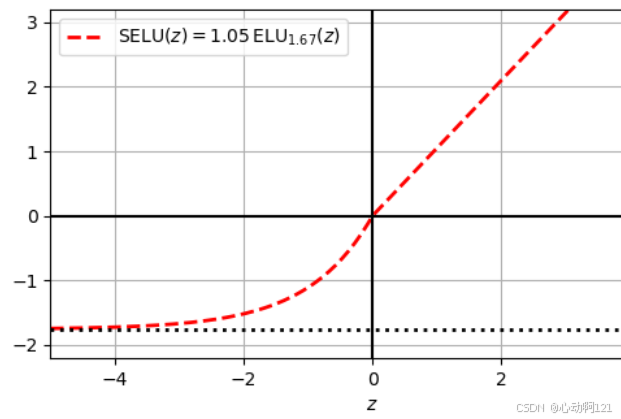
$ELU_\alpha (x) =\lambda \begin{cases} \alpha (e^x-1) ,& x<0 \\x, & x \geqslant 0 \end{cases}$

该神经网络通过自归一化（各层的输出在训练过程中自动保持均值为0、方差为1的分布状态）解决梯度消失和梯度爆炸问题。

自归一化实现的条件：使用LeCun正态初始化、输入特征需要标准化、不能使用批归一化，只能用普通的MLP来保证自归一化属性、不能用正则化技术。

特性	ELU	SELU
全称	指数线性单元	缩放指数线性单元
核心目标	改善 ReLU 的缺点，提供平滑负输出	实现自归一化，替代批归一化
公式特点	$ELU(x) = \begin{cases} x &, x \geqslant 0 \\ \alpha (e^x - 1)&, x < 0 \end{cases}$	$\text{SELU}(x) = \lambda \cdot \text{ELU}(x, \alpha)$
参数	$\alpha$ 通常为 1，可调	$\alpha \approx 1.6733,\lambda \approx 1.0507$ (固定)
优点	缓解死亡ReLU；输出接近零均值；平滑	自归一化；缓解梯度消失/爆炸；继承ELU优点
缺点	计算量稍大	使用限制严格（初始化、结构等）
适用场景	替代 ReLU，希望获得更稳定训练的通用场景	深层全连接网络，希望尝试不使用 BN 的架构
keras使用	activation=“elu” activation=tf.keras.layers.ELU()	acivation="selu"

tf.random.set_seed(42)
model = tf.keras.Sequential()
model.add(tf.keras.layers.Flatten(input_shape=[28, 28]))
for layer in range(100):model.add(tf.keras.layers.Dense(100, activation="selu",kernel_initializer="lecun_normal"))
model.add(tf.keras.layers.Dense(10, activation="softmax"))

（3）GELU、Swish和Mish

这三种函数都是“自门控激活函数”，其核心思想是让激活函数能够根据输入值的大小，自适应的决定“通过”多少信息，而不是像ReLU那样简答的二值化。

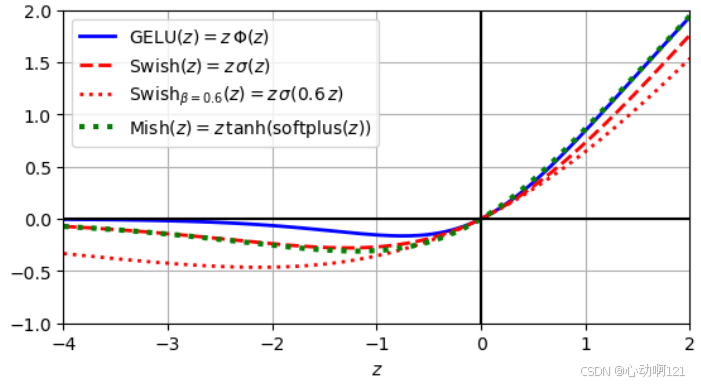
高斯误差线性单元GELU：激活值不仅应由输入是否大于0来决定，还应该考虑到输入值在有多大的概率会被选中。其公式为： $GELU(x) = x \cdot \Phi(x)$ ，它是处处平滑的，有利于梯度计算。在x很大的时候，函数的输出值接近1；当 x 很小的时候函数输出接近于0；对中间值的x，输出x的一部分，这样达到软门控的效果。

Swish ：看作是一个自门控的 Sigmoid 函数。门控信号来自输入本身，通过一个Sigmoid函数产生一个介于0到1之间的软门控值，然后用这个值来缩放原始输入。和GELU一样是处处平滑的。Sigmoid 函数像一个门控，根据 x 的值来决定让多少信息通过。大的正值，门控接近1，全部通过；大的负值，门控接近0，完全抑制。有趣的是，在 x 为负的区间，函数值不是0，而是一个很小的负值，这有助于增加梯度流，缓解死神经元问题。

Mish：是在Swish的基础上进一步改进的激活函数，在许多视觉任务中这个函数会表现的更好。它的设置目标是追求更好的平滑性和非单调性，比上边两个函数更加平滑，能够有助于更好的梯度流动和信息深入网络。同时，也采用了自门控的思想，使用 $x \cdot \tanh(\ln(1 + e^x))$ 这个函数在负值区域具有更丰富的表现力。

特性	GELU	Swish	Mish
核心思想	基于正态分布概率的门控	基于Sigmoid的自门控	基于tanh(softplus)的自门控
公式	$x \cdot \Phi(x)$ ， $\Phi(x)$ 是标准正态分布的累计分布函数	$x \cdot \sigma(\beta x)$	$x \cdot \tanh(\ln(1 + e^x))$
平滑性	平滑	平滑	极致平滑
单调性	单调	单调	非单调（负区间有驼峰）
下界	~0	~0	~-0.31
上界	∞	∞	∞
主要应用领域	NLP（Transformer）	CV, NLP	CV（目标检测等）
计算成本	较高（近似计算）	中等（需计算sigmoid）	较高（需计算exp、log、tanh）
keras使用	activation="gelu"	activation=“swish” activation=tf.keras.activations.swish def swish(x): return x * tf.sifmoid(x) activation=swish	# 方法1：自定义 def mish(x): return x * tf.math.tanh(tf.math.softplus(x)) activation=mish # 方法2：使用TensorFlow Addons (需安装) # import tensorflow_addons as tfa # activation=tfa.activations.mish

（4）如何选择激活函数

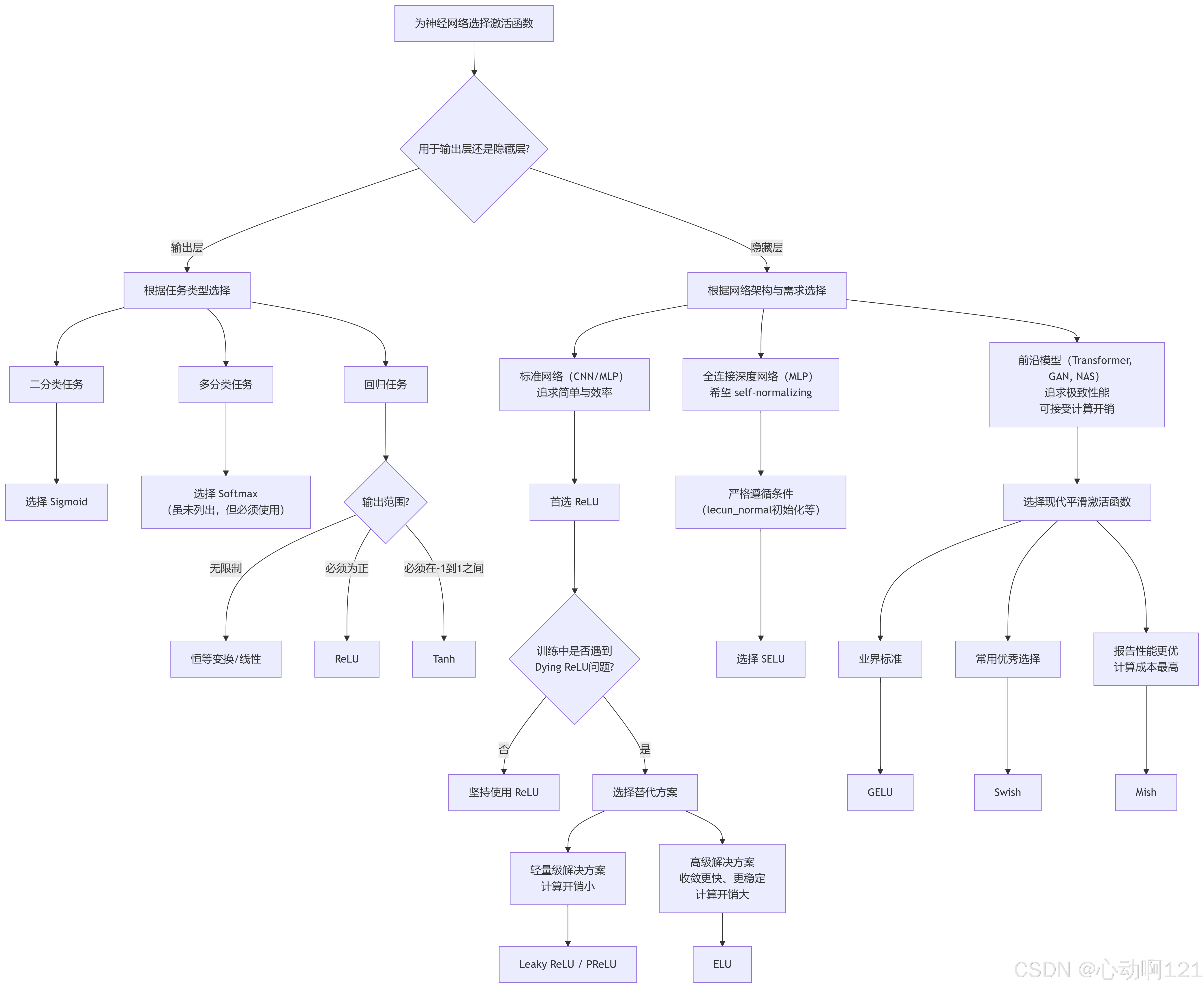
对于隐藏层：

ReLU仍然是简单任务的良好默认选择，它通常与更复杂的激活函数一样好，而且计算速度非常快，许多库和硬件加速器提供特定于ReLU的优化方式。

对于复杂的任务，Swish可能是更好的默认设置，对于非常复杂的任务，甚至可以尝试使用具有可学习的β参数的参数化Swish。Mish可能会带来更好的结果，但它需要更多的计算量。

如果你非常关心运行时延迟，那可能更喜欢leaky ReLU，或者适合复杂任务的参数化leaky ReLU。

对于深度MLP，请尝试使用SELU，但请确保遵守前面列出的约束。如果你有空闲时间和计算能力，也可以使用交叉验证来评估其他激活函数。 Keras开箱即用地支持GELU和Swish；只需使用activation="gelu"或activation="swish"。但是，它还不支持Mish或广义的Swish激活函数。

# 随堂练习：尝试使用gelu/switch / 参数化的leak relu(tf.keras.Layers.PReLU)
tf.random.set_seed(42)
model = tf.keras.Sequential()
model.add(tf.keras.layers.Flatten(input_shape=[28, 28]))
for layer in range(2):# model.add(tf.keras.layers.Dense(50, activation="gelu",kernel_initializer="lecun_normal"))model.add(tf.keras.layers.Dense(50, kernel_initializer="lecun_normal"))model.add(tf.keras.layers.PReLU())
model.add(tf.keras.layers.Dense(10, activation="softmax"))model.compile(loss="sparse_categorical_crossentropy",optimizer=tf.keras.optimizers.SGD(learning_rate=0.001),metrics=["accuracy"])

3、批量归一化（Batch Normalization）

（1）理论

该技术包括在模型中每个隐藏层的激活函数之前或之后添加一个操作。该技术的核心思想是在网络的每一层，对输入该层的数据进行归一化，使其均值为0、方差为1之后再进行缩放和平移。

该操作对每个输入进行零中心并归一化，为了使输入零中心化并归一化，该算法需要估计每个输入的均值和标准差。我们通过评估当前小批次上的输入的均值和标准差（因此称为“批量归一化”）来实现。

在许多情况下，如果将 BN 层添加为神经网络的第一层，则无须归一化训练集（也就是说，不需要使用 `StandardScaler` 或 `Normalization`），BN 层会为你完成此操作（因为它一次只能查看一个批次，它还可以重新缩放和偏移每个输入特征）。

工作流程：标准化 —— 缩放平移

标准化：计算该批次数据在每个特征维度上的均值和方差，然后在均值和方差将数据标准化维均值为0、方差为1的分布。

缩放平移：仅仅标准化会改变层原本的表示能力。假如使用sigmoid函数，标准化后的数据会集中在线性区域，失去了非线性特征。因此BN引入两个可学习的参数 $\gamma \text{ and } \beta$ ，对标准化后的数据进行缩放和平移。 $y_i = \gamma \hat{x_i} + \beta= \text{BN}{\gamma, \beta}(x_i)$

特性	描述
目的	减少内部协变量偏移，加速训练，稳定过程
位置	通常置于`全连接/卷积层`之后，`激活函数`之前
操作	1. 标准化：减去批次均值，除以批次标准差 2. 缩放平移：乘以$\gamma$，加上$\beta$（可学习参数）
训练/推理	训练：使用当前批次的统计量推理：使用全局（移动平均）统计量
优点	加速收敛、允许高学习率、缓解梯度消失、有正则化效果、j降低对初始化的敏感度
局限	依赖足够大的Batch Size，在RNN中应用不便

批量归一化算法的计算过程：

$\mu_B = \frac{1}{m_B} \sum_{i=1}^{m_B} \mathbf{x}^{(i)}$$\\\\$ $\mu_B$ 是输入均值的向量，在整个小批次B上评估（每个输入包含一个均值）， $m_B$ 是小批次中的实例数量

$\sigma_B^2 = \frac{1}{m_B} \sum_{i=1}^{m_B} (\mathbf{x}^{(i)} - \mu_B)^2\\ \\$ ， $\sigma _B$ 是输入标准差的向量，也在整个小批次上的评估（每个输入一个标准差）

$\hat{\mathbf{x}}^{(i)} = \frac{\mathbf{x}^{(i)} - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\\$ ， $\epsilon$ 是一个平滑项，用于避免除以0（是一个很小的值）；

$\mathbf{z}^{(i)} = \boldsymbol{\gamma} \otimes \hat{\mathbf{x}}^{(i)} + \boldsymbol{\beta}$ ， $\boldsymbol{\gamma}$ 是层的缩放参数向量（每个输入一个缩放参数）； $\boldsymbol{\beta}$ 是层的偏移参数向量； $\otimes$ 表示逐元素惩罚（每个输入乘以其相应的输出缩放参数）； $\mathbf{z}^{(i)}$ 是 BN 操作的输出，将传递给下一层或激活函数。

在测试/推理时，我们常常需要处理单个实例或一个不可靠的小批量，但是无法像训练时那样计算出一个有统计意义的批次均值和方差。在理论上，可以在结束训练后遍历整个训练集，之后为每个BN层计算均值和方差；在实际上是在训练过程中，使用指数移动平均（EMA）来动态、平滑地估算整个训练集地全局统计量。

每个BN层管理四个参数向量： $\gamma$ 缩放向量，可学习参数； $\beta$ 偏移向量，可学习参数； $\mu$ 均值向量，通过指数移动平均估算得到； $\sigma$ 标准差向量，通过指数移动平均估算到。

γ和 β：像普通的权重一样，通过反向传播和梯度下降进行学习和优化。μ 和 σ：在训练过程中，每个批次都会计算当前的 μ_B 和 σ_B。然后使用这些批次统计量来更新移动平均值和标准差。

训练时：使用当前批次的 μ_B 和 σ_B 来归一化数据，并使用它们来更新移动平均。

测试/推理时：停止更新移动平均。固定使用训练阶段估算好的最终 moving_mean 和moving_variance 来归一化数据。

最后，批量归一化的作用之一就是正则化，大大减少了对其他正则化技术的需求。但是，批量归一化确实增加了模型的复杂度。

（2）在keras中的使用

与使用Keras的大多数任务操作一样，实施批量归一化非常简单，只需在每个隐藏层的激活函数之前或之后添加一个BatchNormalization层。也可以添加一个BN层作为模型的第一层，但是普通的Normalization层在这个位置通常也表现得非常好（它唯一的缺点是必须首先调用它的adapt()方法）。例如，此模型在每个隐藏层之后应用BN,并将其作为模型的第一层（展平层之后)。

model = tf.keras.Sequential([tf.keras.layers.Flatten(input_shape=[28, 28]),tf.keras.layers.BatchNormalization(),tf.keras.layers.Dense(300, activation="relu", kernel_initializer="he_normal"),tf.keras.layers.BatchNormalization(),tf.keras.layers.Dense(100, activation="relu", kernel_initializer="he_normal"),tf.keras.layers.BatchNormalization(),tf.keras.layers.Dense(10, activation="softmax")
])
model.summary()Layer (type)                Output Shape              Param #   
=================================================================flatten_3 (Flatten)         (None, 784)               0         batch_normalization (Batch  (None, 784)               3136      Normalization)                                                  dense_205 (Dense)           (None, 300)               235500    batch_normalization_1 (Bat  (None, 300)               1200      chNormalization)                                                dense_206 (Dense)           (None, 100)               30100     batch_normalization_2 (Bat  (None, 100)               400       chNormalization)                                                dense_207 (Dense)           (None, 10)                1010

其中3136 = 784 * 4，BN层有4个参数，输入的维度是（784，）

235500 = 784 * 300 +300，输入维度是(784,)✖神经元数量300+偏置数量300= 权重参数+偏置参数

要在激活函数之前添加BN层，必须从隐藏层中移除激活函数，并将它们作为单独的层添加到BN层之后。此外，由于批量归一化层的每个输入都包含一个偏移参数，因此你可以在创建它时传递use_bias=False，从上一层中删除偏置项。最后，通常可以删除第一个BN层以避免将第一个隐藏层夹在两个BN层之间，更新后的代码如下所示：

model = tf.keras.Sequential([tf.keras.layers.Flatten(input_shape=[28, 28]),tf.keras.layers.Dense(300, kernel_initializer="he_normal", use_bias=False),tf.keras.layers.BatchNormalization(),tf.keras.layers.Activation("relu"),tf.keras.layers.Dense(100, kernel_initializer="he_normal", use_bias=False),tf.keras.layers.BatchNormalization(),tf.keras.layers.Activation("relu"),tf.keras.layers.Dense(10, activation="softmax")
])

BatchNormalization函数可调整的超参数：momentum的值通常接近1，例如0.9、0.99、0.999，对于较大的数据集和较小的批处理需要更多的9；axis的值确定在哪个轴被归一化，默认是-1，希望在哪些维度计算统计量把哪些维度放到axis参数中。

4、梯度裁剪

（1）理论

这是专门针对梯度爆炸问题的直接方法。它为梯度设置一个上限阈值，当梯度超过这个阈值时，就将其裁剪到这个值。其核心思想是在反向传播计算完梯度之后、使用优化器更新模型参数之前，对梯度向量的模长或最大值进行限制，确保不会超过一个预设的阈值。通常用于循环神经网络（RNN），很难使用批量归一化。

方法一：按值裁剪

为每个梯度元素设置一个上限和下限，任何超过这个范围的梯度值都会被截断（超出最大值就直接按最大值算，超出最小值就按最小值算）。但是这样可能会改变梯度方向，因为它独立的处理每个元素，裁剪后的梯度方向可能与原始方向不同。

方法二：按模裁剪（常用的方法）

关注整个梯度向量的模长，如果模长超过阈值，就将整个向量按比例缩放，使其模型等于阈值，而保持方向不变。将梯度向量g进行L2正则化

（2）在keras中的使用

在keras中只需要在创建优化器的时候设置clipvalue\clipnorm参数。

optimizer = tf.keras.optimizers.SGD(clipvalue = 1.0)

clipvalue=1.0是按值裁剪，将梯度向量的每个分量都裁剪为-1~1之间的值，意味着损失函数的所有偏导数将限制在这个范围之内。可能会改变梯度向量的方向，例如，如果原始梯度向量为[0.9，100.0]，则其主要指向第二个轴的方向，但是按值裁剪后，将得到[0.9，1.0]，这将大致指向两个轴之间的对角线。实际上，这种方法非常有效。

optimizer = tf.keras.optimizers.SGD(clipnorm = 1.0)

clipnorm=1.0是按模裁剪，可以将梯度向量的L2范数限制在1.0之内。例如，向量[0.9，100.0]将被裁剪为[0.00899964，0.9999595]，它保留了方向，但几乎消除了第一个分量。

二、有效数据少——重用预训练层

如果不先尝试找到一个现有的神经网络——该神经网络可以完成与你要处理的任务类似的任务，就从头开始训练非常大的DNN，这通常不是一个好主意。如果能够找到这样的神经网络，那么通常可以重用它的大部分层，除了最上面的层。这种技术称为迁移学习。

它不仅会大大加快训练速度，而且需要的训练数据也会大大减少。假设你可以访问一个训练过的DNN，它能分类100种不同类别的图像，其中包括动物、植物、车辆和日常物品，现在想训练该DNN来对特定类型的车辆进行分类。这些任务非常相似，甚至有部分重叠，因此应该尝试重用第一个网络的一部分。

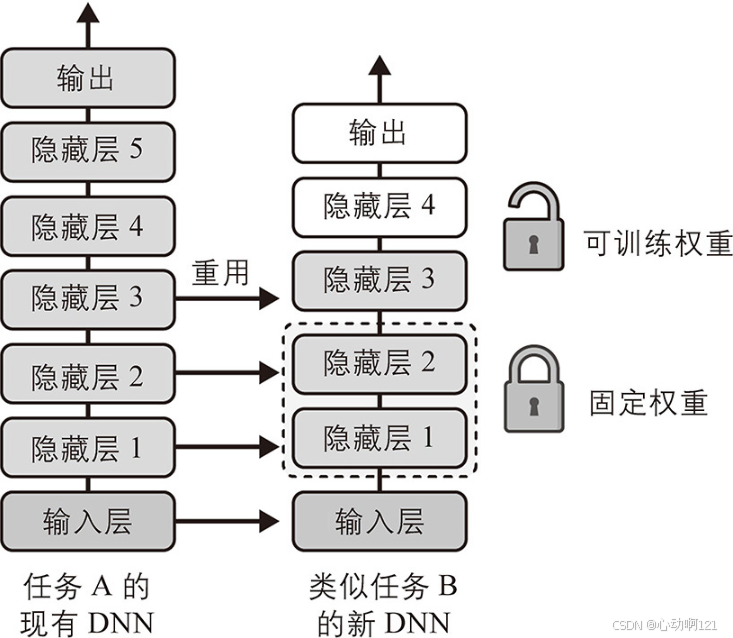
类似地，原始模型上面的隐藏层不太可能像下面的那样有用，因为对新任务最有用的高级特征可能与对原始任务最有用的特征有很大的不同。需要确定要重用的具体层数。任务越相似，可重用的层越多（从较低的层开始）。对于非常相似的任务，请尝试保留所有的隐藏层，只替换掉输出层。

首先，尝试冻结所有可重用的层（即使它们的权重不可训练，以便梯度下降不会修改它们并且它们将保持固定），训练模型并查看其表现。然后，尝试解冻上面隐藏层中的一两层，使反向传播可以对其进行调整，再查看性能是否有所提高。拥有的训练数据越多，可以解冻的层就越多。当解冻重用层时，降低学习率也很有用：这可以避免破坏其已经调整好的权重。如果，仍然无法获得良好的性能，并且训练数据很少，那么试着去掉顶部的隐藏层，然后再次冻结其余所有的隐藏层。不断迭代，直到找到合适的可以重用的层数。如果有大量的训练数据，则可以尝试替换顶部的隐藏层而不是去掉它们，甚至可以添加更多的隐藏层。

1、用keras进行迁移学习

其核心思想是保留这些通用的底层特征，只替换和重新训练模型的顶层、用于特定分类任务的分类器。一般有两种方法：特征提取和微调。

迁移学习的流程：创建基础模型并冻结 —— 添加新的分类头 —— 编译和训练模型 —— 解冻部分层进行训练

如果直接从基础模型中复制模型的前几层，这里的赋值得到的 model_B_on_A 和 model_A 共享网络层。因此，当训练其中一个模型的时候，另一个模型参数也会同步更新。解决此问题只需要基于 model_A 克隆得到model_A_clone（这里需要手动复制下原模型的权重），之后在进行赋值得到 model_B_on_A 。

model_A = tf.keras.models.load_model("./models/my_model_A.keras")
model_A_clone = tf.keras.models.clone_model(model_A)
model_A_clone.set_weights(model_A.get_weights())model_B_on_A = tf.keras.Sequential(model_A_clone.layers[:-1])
model_B_on_A.add(tf.keras.layers.Dense(1, activation="sigmoid"))

在前几个轮次时冻结重用层，给新层一些时间来学习合理的权重。为此，将每一层的trainable属性设置为False并编译模型：

for layer in model_B_on_A.layers[:-1]:layer.trainable = False
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
model_B_on_A.compile(loss="binary_crossentropy", optimizer=optimizer,metrics=["accuracy"])

模型训练几个轮次之后，解冻重用层（需要再次编译模型），并继续进行训练以基于任务B来微调重用层。解冻重用层之后，降低学习率通常可以再次避免损坏重用权重：

history = model_B_on_A.fit(X_train_B, y_train_B, epochs=4,validation_data=(X_valid_B, y_valid_B))
# 解冻： 将每层的 trainable 设置为 True 
for layer in model_B_on_A.layers[:-1]:layer.trainable = True
# 解冻后需要重新编译模型,降低学习率再次避免重用权重
optimizer = tf.keras.optimizers.SGD(learning_rate=0.001)
model_B_on_A.compile(loss="binary_crossentropy", optimizer=optimizer,metrics=["accuracy"])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=16,validation_data=(X_valid_B, y_valid_B))

总结：迁移学习在小型密集网络中不能很好的工作，大概是因为小型网络能够学习的模式很少，密集网络学习的是非常具体的模式，这在其他任务中不是很有用。迁移学习最适合用于深度卷积层神经网络，后者倾向于学习更为通用的特征检测器（尤其是在较低层）。

2、无监督预训练

无监督预训练主要解决两个核心问题：数据标签的稀缺和昂贵、模型泛化能力不足。

如果收集大量未标记的训练数据，尝试使用它们来训练无监督模型，例如自动编码器或生成对抗网络（GAN）。然后，可以重用自动编码器的较低层或GAN判别器的较低层，在顶部添加针对自己的任务的输出层，并使用监督学习（即使用带有标签的训练实例）来微调最终的网络。

在监督训练中，使用无监督学习技术基于所有数据（包括未标记数据）训练模型，然后使用监督学习技术基于带标签的数据针对最终任务进行微调；无监督部分可以一次训练一层，也可以直接训练整个模型：

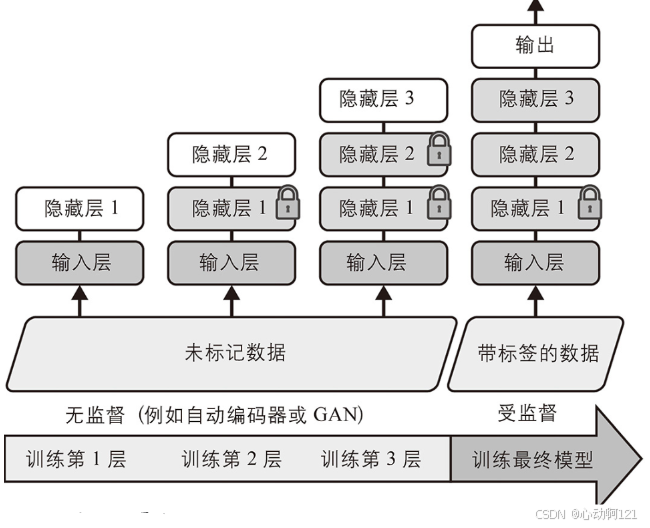
总之，解决的任务复杂，没有可重用的相似模型，带标签的训练数据很少，但是无标签的训练数据很多时，无监督预训练（GAN/自动编码器）是个不错选择。

3、基于辅助任务的预训练

其核心思想是：为了让模型学习到高质量、通用、可迁移的表示，我们不仅仅在最终的目标任务上训练模型，而是先让模型在一系列精心设计的“辅助任务”上进行预训练。

基于辅助任务的预训练可以理解成方法论，无监督学习是实现这种方法论最主要、最强大的手段。

维度	基于辅助任务的预训练	无监督任务的预训练
核心思想	通过完成一个或多个额外任务来学习更好的通用表示。	从无标签数据中自行寻找规律和结构来学习表示。
任务性质	辅助任务可以是监督、无监督或自监督的。	任务一定是无监督或自监督的。
监督信号	可能有人为设计的信号（如词性标签、句法树），也可能没有（如MLM）。	完全没有人工标注的标签。监督信号来自数据自身（如上下文、数据变换）。
关系	一个更广泛的概念。无监督预训练是它的一个子集，并且是