格密码--从FFT到NTT(附源码)
FFT:
引言
FFT最广泛使用的一个领域就是加速多项式相乘。
并且能够把多项式乘法的复杂度从O(n2)O(n^2)O(n2)降低到O(nlogn)O(nlogn)O(nlogn)。传统的我们计算两个多项式相乘如:A(x)=x2+3x+2A(x)=x^2+3x+2A(x)=x2+3x+2与B(x)=2x2+1B(x)=2x^2+1B(x)=2x2+1计算C(x)=A(x)⋅B(x)C(x)=A(x)\cdot B(x)C(x)=A(x)⋅B(x)则
C(x)=(x2+3x+2)(2x2+1)=x2(2x2+1)+3x(2x2+1)+2(2x2+1)=2x4+x2+6x3+3x+4x2+2=2x4+6x3+5x2+3x+2\begin{aligned} C(x) &= (x^2 + 3x + 2)(2x^2 + 1) \\ &= x^2(2x^2 + 1) + 3x(2x^2 + 1) + 2(2x^2 + 1) \\ &= 2x^4 + x^2 + 6x^3 + 3x + 4x^2 + 2 \\ &= 2x^4 + 6x^3 + 5x^2 + 3x + 2 \end{aligned} C(x)=(x2+3x+2)(2x2+1)=x2(2x2+1)+3x(2x2+1)+2(2x2+1)=2x4+x2+6x3+3x+4x2+2=2x4+6x3+5x2+3x+2
上面是我们通常计算多项式相乘的时候所用到的朴素算法(如果两个相乘的多项式都是n次的话,那么计算其相乘的效率就是O(n2)O(n^2)O(n2)),不同于此基于FFT可以构造一种更加复杂但是有效的计算方式。
多项式的存储
首先:我们思考要如何存储一个多项式?
答案有两个:
1.系数表示法
A(x)=x2+3x+2→A=[2,3,1]A(x)=x^2+3x+2 \quad\rightarrow \quad A=[2,3,1]A(x)=x2+3x+2→A=[2,3,1]
B(x)=2x2+1→B=[1,0,2]B(x)=2x^2+1\quad\rightarrow \quad B=[1,0,2]B(x)=2x2+1→B=[1,0,2],
C(x)=2x4+6x3+5x2+3x+2→C=[2,3,5,6,2]C(x)=2x^4+6x^3+5x^2+3x+2 \quad \rightarrow \quad C=[2,3,5,6,2]C(x)=2x4+6x3+5x2+3x+2→C=[2,3,5,6,2]
2.值表示法
注:值表示法并不具有普遍性,因为通过值表示我们无法便捷得知x任意取值所得到的y的值
多项式插值的唯一性定理:
若给定 d+1d + 1d+1 个横坐标互不相同的点 (x0,y0),(x1,y1),…,(xd,yd)(x_0, y_0), (x_1, y_1), \dots, (x_d, y_d)(x0,y0),(x1,y1),…,(xd,yd)(即所有 xix_ixi 互不相等),则存在且仅存在一个次数不超过 ddd 的多项式 P(x)P(x)P(x),使得对所有 i=0,1,…,di = 0, 1, \dots, di=0,1,…,d,都满足 P(xi)=yiP(x_i) = y_iP(xi)=yi。
解释:任意一d阶多项式都由d+1个点唯一确定。
证明:
对于d次多项式:P(x)=p0+p1x+p2x2+⋯+pdxdP(x) = p_0 + p_1 x + p_2 x^2 + \dots + p_d x^dP(x)=p0+p1x+p2x2+⋯+pdxd
其存在d+1个互不相同的点:(x0,P(x0)),(x1,P(x1)),⋯,(xd,P(xd)){(x_0,P(x_0)),(x_1,P(x_1)),\cdots,(x_d,P(x_d))}(x0,P(x0)),(x1,P(x1)),⋯,(xd,P(xd))
代入点,可得方程组
{P(x0)=p0+p1x0+p2x02+⋯+pdx0dP(x1)=p0+p1x1+p2x12+⋯+pdx1d⋮P(xd)=p0+p1xd+p2xd2+⋯+pdxdd\begin{cases} P(x_0) = p_0 + p_1 x_0 + p_2 x_0^2 + \dots + p_d x_0^d \\ P(x_1) = p_0 + p_1 x_1 + p_2 x_1^2 + \dots + p_d x_1^d \\ \vdots \\ P(x_d) = p_0 + p_1 x_d + p_2 x_d^2 + \dots + p_d x_d^d \end{cases} ⎩⎨⎧P(x0)=p0+p1x0+p2x02+⋯+pdx0dP(x1)=p0+p1x1+p2x12+⋯+pdx1d⋮P(xd)=p0+p1xd+p2xd2+⋯+pdxdd
矩阵形式:
[P(x0)P(x1)⋮P(xd)]=[1x0x02…x0d1x1x12…x1d⋮⋮⋮⋱⋮1xdxd2…xdd][p0p1⋮pd]\begin{bmatrix} P(x_0) \\ P(x_1) \\ \vdots \\ P(x_d) \end{bmatrix} =\begin{bmatrix} 1 & x_0 & x_0^2 & \dots & x_0^d \\ 1 & x_1 & x_1^2 & \dots & x_1^d \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_d & x_d^2 & \dots & x_d^d \end{bmatrix} \begin{bmatrix} p_0 \\ p_1 \\ \vdots \\ p_d \end{bmatrix} P(x0)P(x1)⋮P(xd)=11⋮1x0x1⋮xdx02x12⋮xd2……⋱…x0dx1d⋮xddp0p1⋮pd
(中间的矩阵为范德蒙德矩阵(Vandermonde matrix))
其中因为 x0,x1,…,xdx_0, x_1, \dots, x_dx0,x1,…,xd 各不相同,则矩阵 MMM 可逆
⇒\Rightarrow⇒ 系数 p0,p1,…,pdp_0, p_1, \dots, p_dp0,p1,…,pd 存在且唯一
⇒\Rightarrow⇒ 多项式 P(x)P(x)P(x) 存在且唯一
多项式相乘计算的新方法:
方法概述:
通常情况下我们习惯于使用系数表示法,但是这种表示方法对于两个多项式相乘运算的效率是O(n2)O(n^2)O(n2),如何改变这种困局,利用值表示法?:
例如:
A(x)=x2+2x+1A(x) = x^2 + 2x + 1A(x)=x2+2x+1
值表示法:[(−2,1),(−1,0),(0,1),(1,4),(2,9)][(-2, 1), (-1, 0), (0, 1), (1, 4), (2, 9)][(−2,1),(−1,0),(0,1),(1,4),(2,9)]
B(x)=x2−2x+1B(x) = x^2 - 2x + 1B(x)=x2−2x+1
值表示法:[(−2,9),(−1,4),(0,1),(1,0),(2,1)][(-2, 9), (-1, 4), (0, 1), (1, 0), (2, 1)][(−2,9),(−1,4),(0,1),(1,0),(2,1)]
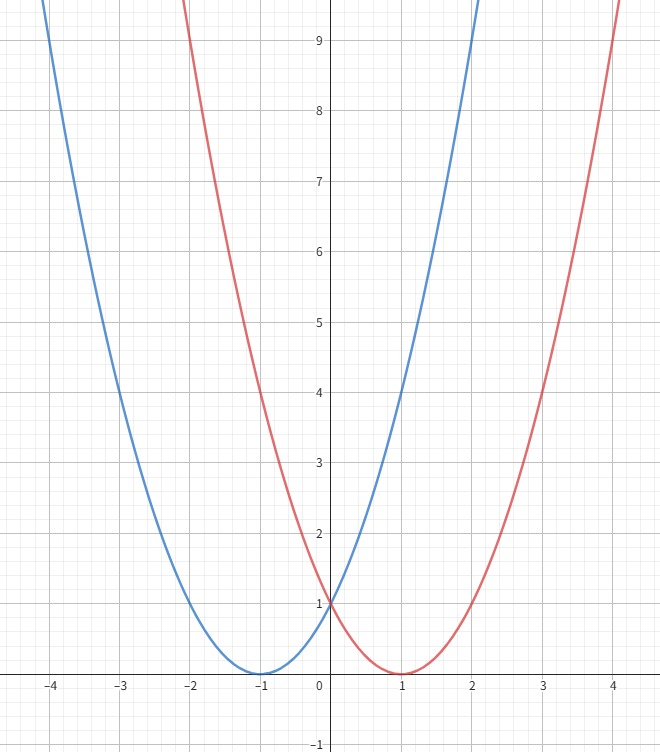
使用值表示法的时:如果想要计算A×BA \times BA×B所得到的CCC的值表示法其实很简单,就是选择大于【A的最大阶数和B的最大阶数相乘所得到阶数(这个阶数是C的最大阶数)】个数的横坐标,然后让相同横坐标的纵坐标相乘,横坐标保持不变,所得到的就是CCC上某一点的坐标。例如上面:AAA的最大阶数是2,BBB的最大阶数也是2,可得CCC的最大阶数应该是4,选择的坐标个数应该大于其阶数
[(−2,1),(−1,0),(0,1),(1,4),(2,9)][(-2, 1), (-1, 0), (0, 1), (1, 4), (2, 9)][(−2,1),(−1,0),(0,1),(1,4),(2,9)]
×[(−2,9),(−1,4),(0,1),(1,0),(2,1)]\times[(-2, 9), (-1, 4), (0, 1), (1, 0), (2, 1)]×[(−2,9),(−1,4),(0,1),(1,0),(2,1)]
=[(−2,9),(−1,0),(0,1),(1,0),(2,9)]=[(-2, 9), (-1, 0), (0, 1), (1, 0), (2, 9)]=[(−2,9),(−1,0),(0,1),(1,0),(2,9)]
将上面的值表示法 [(−2,9),(−1,0),(0,1),(1,0),(2,9)][(-2, 9), (-1, 0), (0, 1), (1, 0), (2, 9)][(−2,9),(−1,0),(0,1),(1,0),(2,9)]转化为系数表示法:
C(x)=x4−2x2+1C(x) = x^4 - 2x^2 + 1C(x)=x4−2x2+1
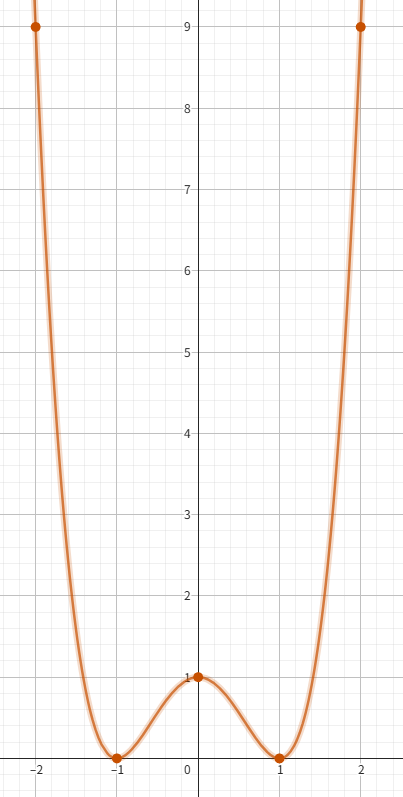
存在的问题:
通过上面的运算看似更加简便了,然而复杂度却提升到了O(nd)O(nd)O(nd)(n是选择的坐标点数,d是阶数)注:O(d)O(d)O(d)是因为对每一个点带入计算值的复杂度,O(n)O(n)O(n)是因为坐标点的个数,因为每一个点都要带入计算值,所以可得到所有的值计算的效率就是O(nd)O(nd)O(nd)
上述的操作可以用下面的图来表示:

解决问题:
如何对其进行优化?这里的优化主要是对点带入求值的优化,也就是系数表示法转化为值表示法的优化。这正是FFT发挥作用的时候了!
利用奇偶性和递归思想:
简化问题:
对于P(x)=x2P(x) = x^2P(x)=x2
如果要选择8个点应该选哪些点? 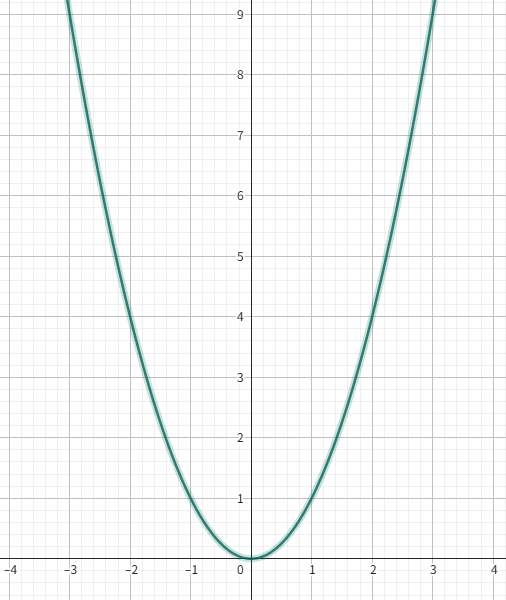
在奇偶函数情况下
只需要计算一半数量点,另一半可以从奇偶性中得出:
(1,1)→(−1,1)(2,4)→(−2,4)(3,9)→(−3,9)(4,16)→(−4,16)\begin{aligned} (1, 1) &\rightarrow (-1, 1) \\ (2, 4) &\rightarrow (-2, 4) \\ (3, 9) &\rightarrow (-3, 9) \\ (4, 16) &\rightarrow (-4, 16) \end{aligned} (1,1)(2,4)(3,9)(4,16)→(−1,1)→(−2,4)→(−3,9)→(−4,16)
举例:
P(x)=3x5+2x4+x3+7x2+5x+1P(x) = 3x^5 + 2x^4 + x^3 + 7x^2 + 5x + 1P(x)=3x5+2x4+x3+7x2+5x+1
P(x)=(2x4+7x2+1)+(3x5+x3+5x)P(x) = (2x^4 + 7x^2 + 1) + (3x^5 + x^3 + 5x)P(x)=(2x4+7x2+1)+(3x5+x3+5x)
把多项式拆奇偶两部分
=(2x4+7x2+1)⏟Pe(x2)+x⋅(3x4+x2+5)⏟Po(x2)= \underbrace{(2x^4 + 7x^2 + 1)}_{P_e(x^2)} + x \cdot \underbrace{(3x^4 + x^2 + 5)}_{P_o(x^2)}=Pe(x2)(2x4+7x2+1)+x⋅Po(x2)(3x4+x2+5)
{P(x)=Pe(x2)+x⋅Po(x2)P(−x)=Pe(x2)−x⋅Po(x2)\begin{cases} P(x) = P_e(x^2) + x \cdot P_o(x^2) \\ P(-x) = P_e(x^2) - x \cdot P_o(x^2) \end{cases}{P(x)=Pe(x2)+x⋅Po(x2)P(−x)=Pe(x2)−x⋅Po(x2) ← lot of overlap
Pe(x2)=2x4+7x2+1P_e(x^2) = 2x^4 + 7x^2 + 1Pe(x2)=2x4+7x2+1
Po(x2)=3x4+x2+5P_o(x^2) = 3x^4 + x^2 + 5Po(x2)=3x4+x2+5
Pe(x2)P_e(x^2)Pe(x2) Po(x2)P_o(x^2)Po(x2)都仅仅只有两阶 ,且和原始多项式P(x)P(x)P(x)类似的有奇有偶的多项式
这让我们想到了递归的思想
抽象如下:


目的:多项式系数表示法转化为值表示法,所以我们需要选点和求值
1.对于n-1阶的多项式P(x)P(x)P(x),我们需要选择n个点,要求n个点在原点两侧均匀对称分布(奇偶性)
2.根据每一项xxx的阶数将P分为奇偶两部分分别为PoP_oPo和PeP_ePe,将P0P_0P0和PeP_ePe对应的二次项作为整体(类似换参)又可以得到和原始多项式P(x)P(x)P(x)类似的有奇有偶的多项式,只不过其最高阶已经变为n/2−1n/2-1n/2−1,简化了问题(递归思想)
3.回到第一步(如此递归)
出现新问题:(递归条件不符合)
但是这样做我们也引入了新的问题:
在上述的递归操作中我们假设了每个多项式都选择相反数(对称点)来求值,然而对于子问题而言,每一个求值点都是平方数即都是正数,所以递归操作不成立!!
引入复数域单位根:
我们能不能把这些新的求值点弄成相反数呢?———复数!
所以我们要挑选一些复数使得其平方之后依旧是正负成对出现的
例子:
对于多项式P(x)=x3+x2−x−1P(x)=x^3+x^2-x-1P(x)=x3+x2−x−1
递归函数真正开始运算的过程是如下图:
即:从x1,−x1,x2,−x2x_1,-x_1,x_2,-x_2x1,−x1,x2,−x2到x12,−x12x_1^2,-x_1^2x12,−x12最后到x14x_1^4x14
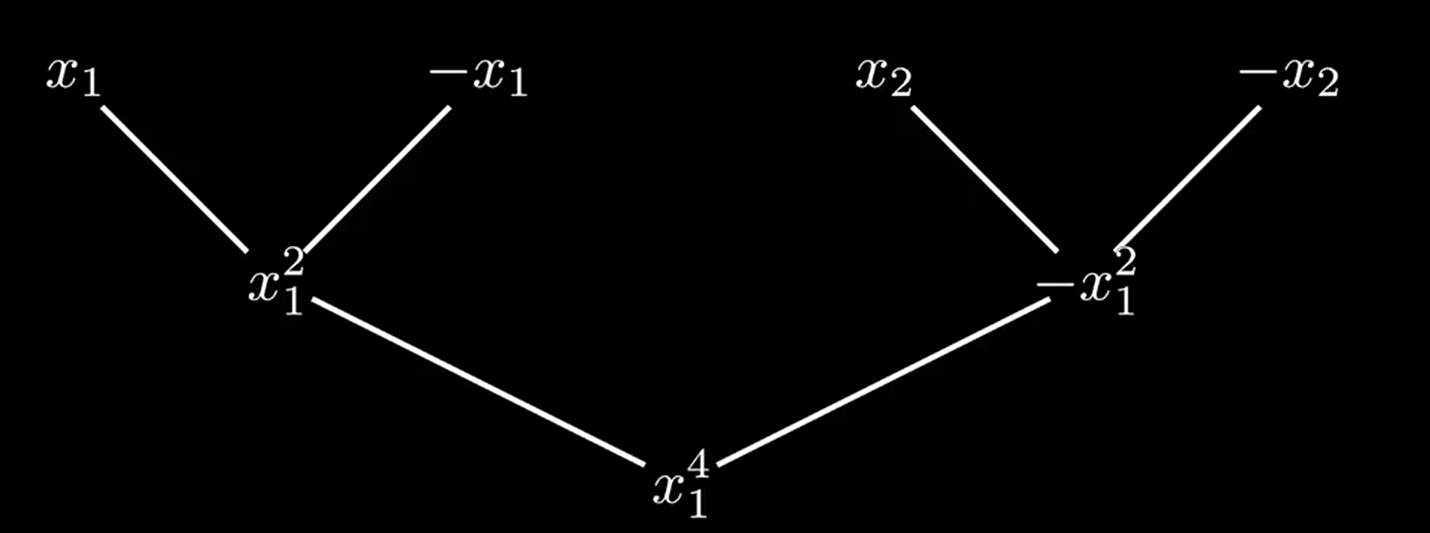
因为对x1x_1x1的赋值可以由我们掌控,不妨引入x1=1x_1=1x1=1,(引入四次单位根问题)
则求解所有的根就是解方程:x14=1x_1^4=1x14=1
同样的思路对于P(x)=x5+2x4−x3+x2+1P(x)=x^5+2x^4-x^3+x^2+1P(x)=x5+2x4−x3+x2+1
为求解8次单位根问题
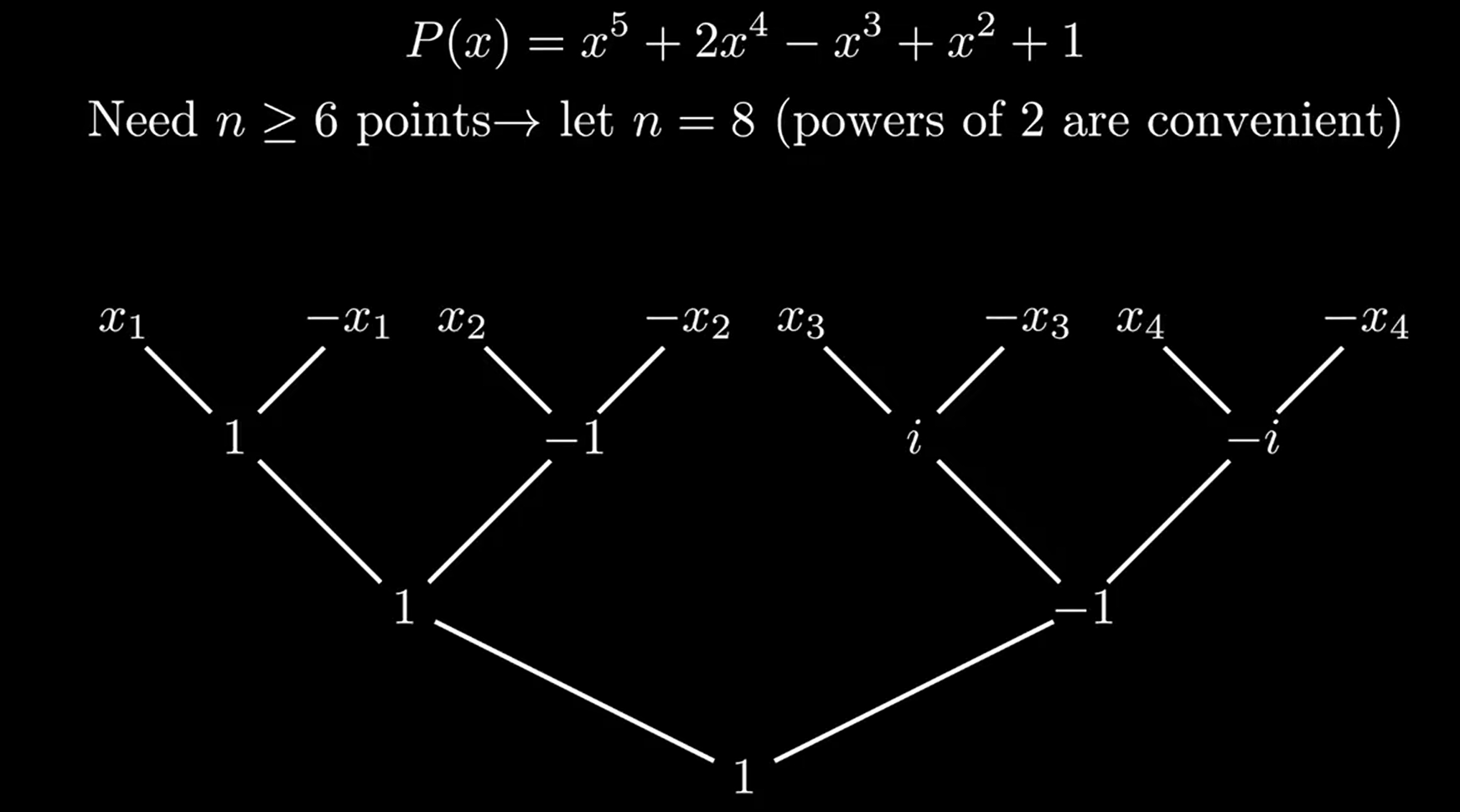
接下来我们将了解一下1的n次方根问题(n次单位根问题)提问:为什么n次方根就可以用于递归过程呢?
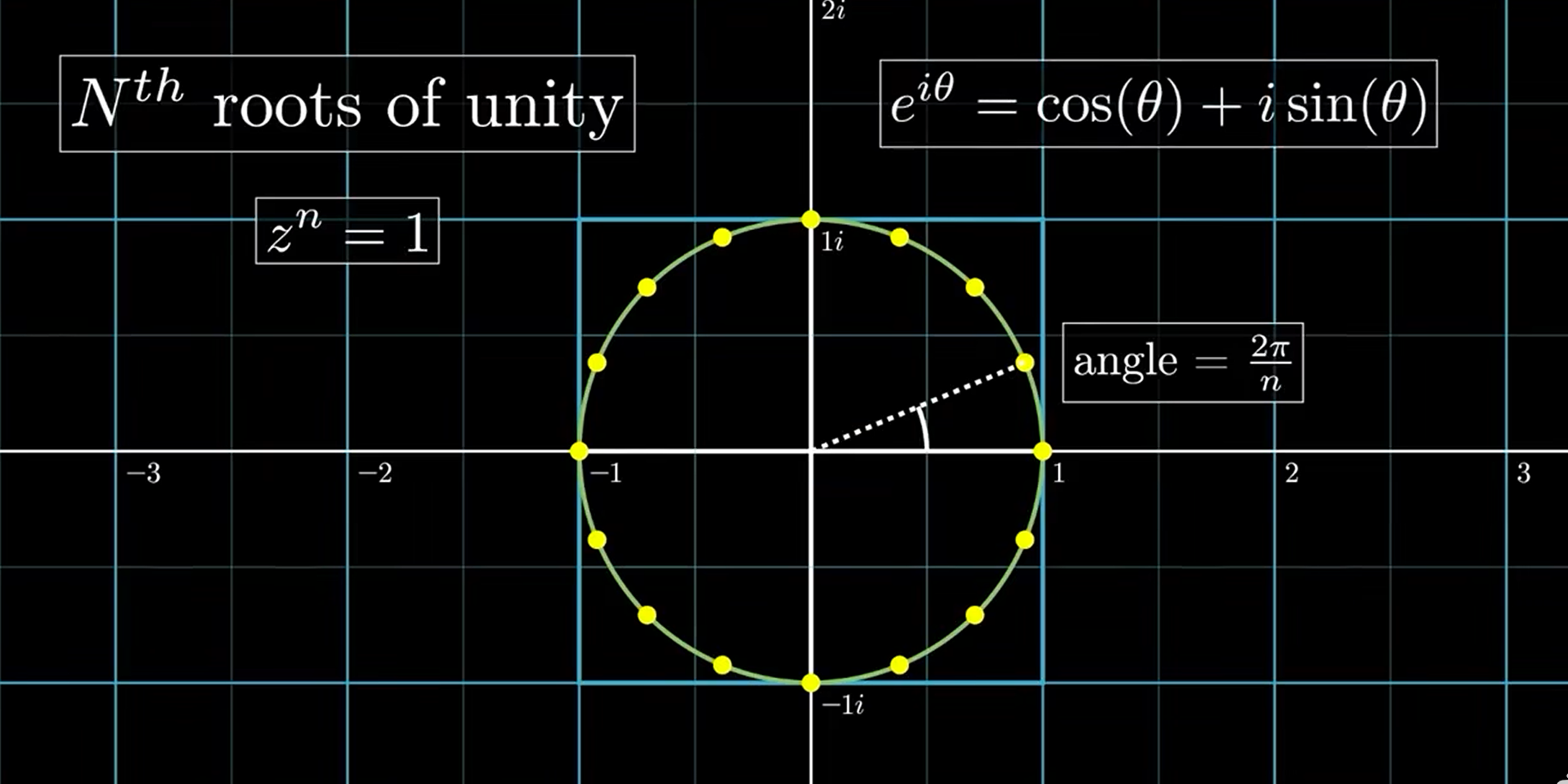
1的n次方根可以被解释为复平面上沿着单位圆等距排布的一系列点,且任意两点之间的夹角就是2πn\frac{2\pi} {n}n2π,在复平面我们使用欧拉公式来描述此:eiθ=cosθ+isinθe^{i\theta} = \cos\theta + i\sin\thetaeiθ=cosθ+isinθ
[欧拉公式描述了复数域中虚指数函数eiθe^{i\theta}eiθ 与三角函数 $\cos\theta ,,,i\sin\theta的等价关系,复数极坐标下的角度(辐角的等价关系,复数极坐标下的角度(辐角的等价关系,复数极坐标下的角度(辐角 \theta )则是复平面内该复数对应点与原点连线和实轴正方向的夹角,满足)则是复平面内该复数对应点与原点连线和实轴正方向的夹角,满足)则是复平面内该复数对应点与原点连线和实轴正方向的夹角,满足\tan\theta = \frac{\text{复数虚部}}{\text{复数实部}}$,并决定复数极坐标形式的方向]
为了更方便的表示,我们定义**ω=e2πin\omega = e^{\frac{2\pi i}{n}}ω=en2πi**(这里的角度θ=2πn\theta=\frac{2\pi}{n}θ=n2π取决于n的值)
之后我们选择的点就是[1,ω1,ω2,⋯,ωn−1][1,\omega^1,\omega^2,\cdots,\omega^{n-1}][1,ω1,ω2,⋯,ωn−1]
一共n个点,如下图所示(i不是变量只是虚数单位):
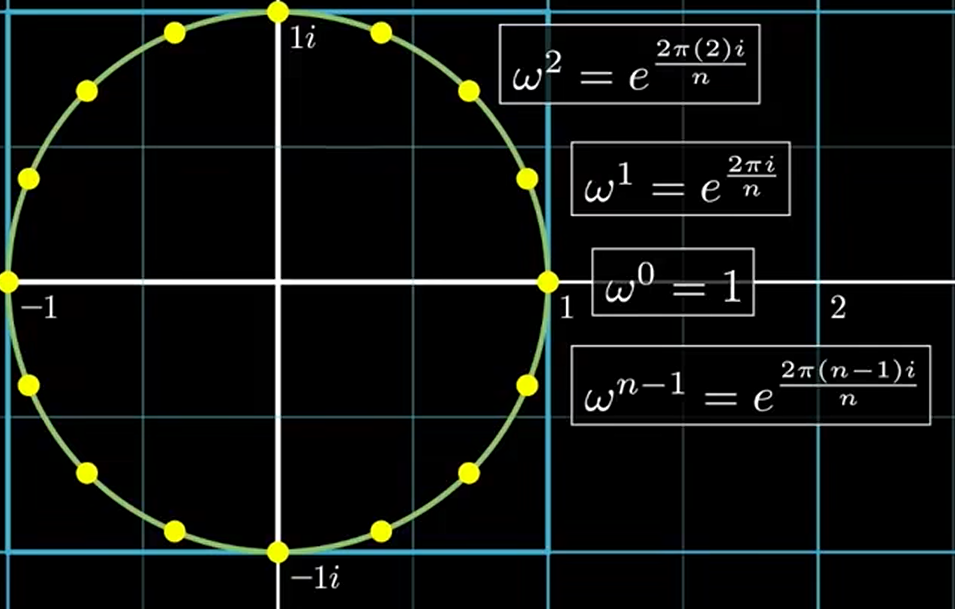
引入复数域单位根之后递归成立的解释:
回到最初的问题:为什么n次方根就可以用于递归过程呢?
reason1:
我们要求所取的点是正负成对的,而这里的ω(j+n2)=−ωj\omega^{(j+\frac{n}{2})}=-\omega^jω(j+2n)=−ωj正好是这一对(见下面的虚线)
reason2:
平方之后的n2\frac{n}{2}2n个n2\frac{n}{2}2n次方根,它们也是正负配对的,完美适配本算法的递归条件
FFT流程和伪代码:

其他都好理解,主要是这一块:

首先数组yyy是用来存储值的,第m个位置对的是次根ωm\omega^mωm(ωm=e2πmin\omega^m = e^{\frac{2\pi m i}{n}}ωm=en2πmi)
最开始执行这段代码时候是在递归的最底层
P(xj)=Pe(xj2)+xjPo(xj2)P(−xj)=Pe(xj2)−xjPo(xj2)j∈{0,1,…(n/2−1)}\begin{aligned} P(x_j) &= P_e(x_j^2) + x_j P_o(x_j^2) \\ P(-x_j) &= P_e(x_j^2) - x_j P_o(x_j^2) \\ j &\in \{0, 1, \dots (n/2 - 1)\} \end{aligned} P(xj)P(−xj)j=Pe(xj2)+xjPo(xj2)=Pe(xj2)−xjPo(xj2)∈{0,1,…(n/2−1)}
由于我们规定xj=wjx_j=w^jxj=wj上式可以改写为:
P(ωj)=Pe(ω2j)+ωjPo(ω2j)P(−ωj)=Pe(ω2j)−ωjPo(ω2j)j∈{0,1,…,(n/2−1)}\begin{aligned} P(\omega^j) &= P_e(\omega^{2j}) + \omega^j P_o(\omega^{2j}) \\ P(-\omega^j) &= P_e(\omega^{2j}) - \omega^j P_o(\omega^{2j}) \\ j &\in \{0, 1, \dots, (n/2 - 1)\} \end{aligned} P(ωj)P(−ωj)j=Pe(ω2j)+ωjPo(ω2j)=Pe(ω2j)−ωjPo(ω2j)∈{0,1,…,(n/2−1)}
而我们知道−ωj=wj+n/2-\omega^j=w^{j+n/2}−ωj=wj+n/2带入可得:
P(ωj)=Pe(ω2j)+ωjPo(ω2j)P(ωj+n/2)=Pe(ω2j)−ωjPo(ω2j)j∈{0,1,…,(n/2−1)}\begin{aligned} P(\omega^j) &= P_e(\omega^{2j}) + \omega^j P_o(\omega^{2j}) \\ P(\omega^{j+n/2}) &= P_e(\omega^{2j}) - \omega^j P_o(\omega^{2j}) \\ j &\in \{0, 1, \dots, (n/2 - 1)\} \end{aligned} P(ωj)P(ωj+n/2)j=Pe(ω2j)+ωjPo(ω2j)=Pe(ω2j)−ωjPo(ω2j)∈{0,1,…,(n/2−1)}
右侧都写成y的形式:
P(ωj)=ye[j]+ωjyo[j]P(ωj+n/2)=ye[j]−ωjyo[j]j∈{0,1,…,(n/2−1)}\begin{aligned} P(\omega^j) &= y_e[j] + \omega^j y_o[j] \\ P(\omega^{j+n/2}) &= y_e[j] - \omega^j y_o[j] \\ j &\in \{0, 1, \dots, (n/2 - 1)\} \end{aligned} P(ωj)P(ωj+n/2)j=ye[j]+ωjyo[j]=ye[j]−ωjyo[j]∈{0,1,…,(n/2−1)}
由于:数组yyy是用来存储值(理解为函数值或者多项式值)的,第m个位置对的是次根ωm\omega^mωm
y(ωj)=ye[j]+ωjyo[j]y(ωj+n/2)=ye[j]−ωjyo[j]j∈{0,1,…,(n/2−1)}\begin{aligned} y(\omega^j) &= y_e[j] + \omega^j y_o[j] \\ y(\omega^{j+n/2}) &= y_e[j] - \omega^j y_o[j] \\ j &\in \{0, 1, \dots, (n/2 - 1)\} \end{aligned} y(ωj)y(ωj+n/2)j=ye[j]+ωjyo[j]=ye[j]−ωjyo[j]∈{0,1,…,(n/2−1)}
最后以n=4为例对这个分割做一个理解首先我们需要明确P是一个数组,先获取P的长度,需要确保原始的P的长度是2的幂次方。
n=1的时候此时P无法再分割,则其为递归出口
n不等于1时候,对P进行分割为奇PoP_oPo偶PeP_ePe两部分
因为这两部分的性质和原始P类似,所以可以递归处理这两部分。
递归到底层之后n等于1,以下图蓝色箭头这一支为例:
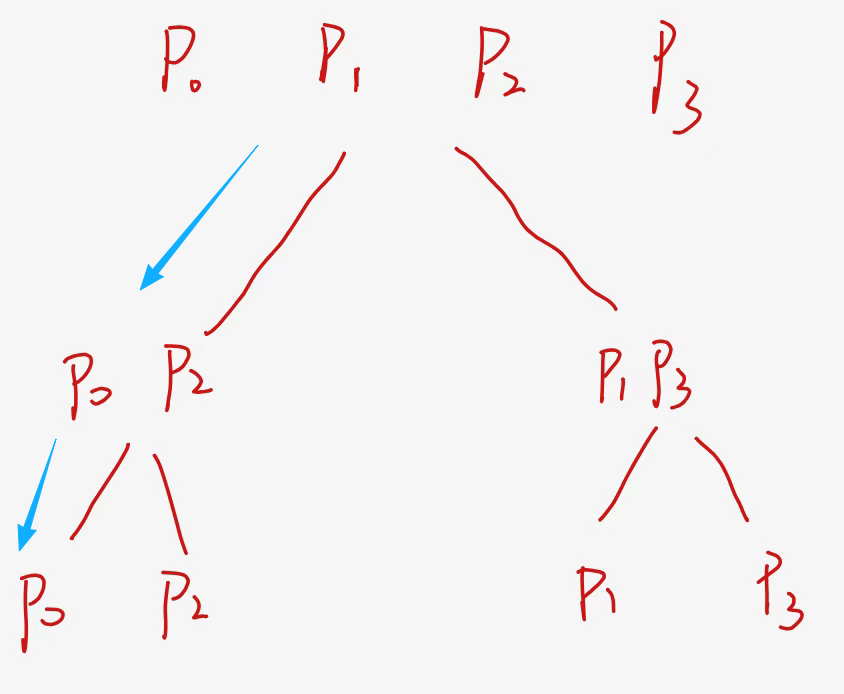 可以得到ye=P(ω0),yo=0y_e=P(\omega^0),y_o=0ye=P(ω0),yo=0,确实无法再次递归了,然后开始执行递归之后的代码:
可以得到ye=P(ω0),yo=0y_e=P(\omega^0),y_o=0ye=P(ω0),yo=0,确实无法再次递归了,然后开始执行递归之后的代码:
y=[0]×ny=[0]\times ny=[0]×n这里所得到的yyy是包含一个元素的数组
此时j只能等于0,可以得到y[0]=ye−ωjyo[j]y[0]=y_e-\omega^jy_o[j]y[0]=ye−ωjyo[j],即可得到y[0]y[0]y[0]也就是p0p_0p0(ω0\omega^0ω0对应的函数值)
同理可以得到p2p_2p2也就是y[1]y[1]y[1]的值。这两次函数返回的值都是单个的取值,等到他们返回上一个递归时候,
继续往下执行此时n=2,所以此时y的长度就是2,在for循环里会执行两次,正好将p0p_0p0和p2p_2p2嵌到y中。
FFT的逆(IFFT):通过系数表示法到值表示法:
结论:IFFT的操作和FFT一模一样,只是把里面的ω\omegaω换成了1nω−1\frac{1}{n}\omega^{-1}n1ω−1

代码也仅仅有一处改动
推导:
对于多项式P(x)=p0+p1x+p2x2+⋯+pn−1xn−1P(x) = p_0 + p_1 x + p_2 x^2 + \dots + p_{n-1} x^{n-1}P(x)=p0+p1x+p2x2+⋯+pn−1xn−1
FFT的通过系数求值的过程可以通过矩阵的形式表示:
[P(x0)P(x1)P(x2)⋮P(xn−1)]=[1x0x02…x0n−11x1x12…x1n−11x2x22…x2n−1⋮⋮⋮⋱⋮1xn−1xn−12…xn−1n−1][p0p1p2⋮pn−1]\begin{bmatrix} P(x_0) \\ P(x_1) \\ P(x_2) \\ \vdots \\ P(x_{n-1}) \end{bmatrix} = \begin{bmatrix} 1 & x_0 & x_0^2 & \dots & x_0^{n-1} \\ 1 & x_1 & x_1^2 & \dots & x_1^{n-1} \\ 1 & x_2 & x_2^2 & \dots & x_2^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n-1} & x_{n-1}^2 & \dots & x_{n-1}^{n-1} \end{bmatrix} \begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ \vdots \\ p_{n-1} \end{bmatrix} P(x0)P(x1)P(x2)⋮P(xn−1)=111⋮1x0x1x2⋮xn−1x02x12x22⋮xn−12………⋱…x0n−1x1n−1x2n−1⋮xn−1n−1p0p1p2⋮pn−1
[P(ω0)P(ω1)P(ω2)⋮P(ωn−1)]=[111…11ωω2…ωn−11ω2ω4…ω2(n−1)⋮⋮⋮⋱⋮1ωn−1ω2(n−1)…ω(n−1)(n−1)][p0p1p2⋮pn−1]\begin{bmatrix} P(\omega^0) \\ P(\omega^1) \\ P(\omega^2) \\ \vdots \\ P(\omega^{n-1}) \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & \dots & 1 \\ 1 & \omega & \omega^2 & \dots & \omega^{n-1} \\ 1 & \omega^2 & \omega^4 & \dots & \omega^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{n-1} & \omega^{2(n-1)} & \dots & \omega^{(n-1)(n-1)} \end{bmatrix} \begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ \vdots \\ p_{n-1} \end{bmatrix} P(ω0)P(ω1)P(ω2)⋮P(ωn−1)=111⋮11ωω2⋮ωn−11ω2ω4⋮ω2(n−1)………⋱…1ωn−1ω2(n−1)⋮ω(n−1)(n−1)p0p1p2⋮pn−1
图中的矩阵我们称为离散傅里叶变换(DFT)矩阵
而通过值求系数(即IFFT)也可以通过矩阵表示:
[p0p1p2⋮pn−1]=[111⋯11ωω2⋯ωn−11ω2ω4⋯ω2(n−1)⋮⋮⋮⋱⋮1ωn−1ω2(n−1)⋯ω(n−1)(n−1)]−1[P(ω0)P(ω1)P(ω2)⋮P(ωn−1)]\begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ \vdots \\ p_{n-1} \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega^2 & \cdots & \omega^{n-1} \\ 1 & \omega^2 & \omega^4 & \cdots & \omega^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{n-1} & \omega^{2(n-1)} & \cdots & \omega^{(n-1)(n-1)} \end{bmatrix}^{-1} \begin{bmatrix} P(\omega^0) \\ P(\omega^1) \\ P(\omega^2) \\ \vdots \\ P(\omega^{n-1}) \end{bmatrix}p0p1p2⋮pn−1=111⋮11ωω2⋮ωn−11ω2ω4⋮ω2(n−1)⋯⋯⋯⋱⋯1ωn−1ω2(n−1)⋮ω(n−1)(n−1)−1P(ω0)P(ω1)P(ω2)⋮P(ωn−1)
化简可得:
[p0p1p2⋮pn−1]=1n[111…11ω−1ω−2…ω−(n−1)1ω−2ω−4…ω−2(n−1)⋮⋮⋮⋱⋮1ω−(n−1)ω−2(n−1)…ω−(n−1)(n−1)][P(ω0)P(ω1)P(ω2)⋮P(ωn−1)]\begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ \vdots \\ p_{n-1} \end{bmatrix} = \frac{1}{n} \begin{bmatrix} 1 & 1 & 1 & \dots & 1 \\ 1 & \omega^{-1} & \omega^{-2} & \dots & \omega^{-(n-1)} \\ 1 & \omega^{-2} & \omega^{-4} & \dots & \omega^{-2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{-(n-1)} & \omega^{-2(n-1)} & \dots & \omega^{-(n-1)(n-1)} \end{bmatrix} \begin{bmatrix} P(\omega^0) \\ P(\omega^1) \\ P(\omega^2) \\ \vdots \\ P(\omega^{n-1}) \end{bmatrix} p0p1p2⋮pn−1=n1111⋮11ω−1ω−2⋮ω−(n−1)1ω−2ω−4⋮ω−2(n−1)………⋱…1ω−(n−1)ω−2(n−1)⋮ω−(n−1)(n−1)P(ω0)P(ω1)P(ω2)⋮P(ωn−1)
这个得到的矩阵和之前的DFT矩阵简直是一模一样的!!!实际上我们只需要把原来的ω\omegaω换成1nω−1\frac{1}{n}\omega^{-1}n1ω−1即可得到新的矩阵
对比二者:

蝴蝶结构:
https://www.youtube.com/watch?v=FaWSGmkboOs
印度老哥讲的视频,还是要对上面的
y[j]=ye[j]+ωjyo[j]y[j+n2]=ye[j]−ωjyo[j]\begin{align} y[j] &= y_e[j] + \omega^j y_o[j] \\ y\left[j + \frac{n}{2}\right] &= y_e[j] - \omega^j y_o[j] \end{align} y[j]y[j+2n]=ye[j]+ωjyo[j]=ye[j]−ωjyo[j]
深刻理解才能得到这个蝴蝶结构
蝴蝶结构从左到右的每一层对应的是递归从低到上的每一层
FFT代码:
import mathdef FFT(P):"""快速傅里叶变换:系数形式 → 点值形式P: 系数列表 [p0, p1, ..., pn-1],n必须是2的幂返回:点值列表 [P(ω⁰), P(ω¹), ..., P(ωⁿ⁻¹)],其中ω是n次单位根"""n = len(P)if n == 1:return P # 递归基:长度为1时直接返回# 计算n次单位根:ω = e^(2πi/n)omega = complex(math.cos(2 * math.pi / n), math.sin(2 * math.pi / n))# 分治:奇偶项分离Pe = P[::2] # 偶下标系数Po = P[1::2] # 奇下标系数ye = FFT(Pe)yo = FFT(Po)# 蝶形运算合并结果y = [0] * nfor j in range(n // 2):y[j] = ye[j] + (omega ** j) * yo[j]y[j + n//2] = ye[j] - (omega ** j) * yo[j]return ydef IFFT(P):"""逆快速傅里叶变换:点值形式 → 系数形式P: 点值列表 [P(ω⁰), P(ω¹), ..., P(ωⁿ⁻¹)]返回:系数列表 [p0, p1, ..., pn-1]"""n = len(P)if n == 1:return P # 递归基:长度为1时直接返回# 计算逆单位根:ω = (1/n) * e^(-2πi/n)omega = complex(math.cos(2 * math.pi / n), -math.sin(2 * math.pi / n)) / n# 分治:奇偶项分离(与FFT对称)Pe = P[::2]Po = P[1::2]ye = IFFT(Pe)yo = IFFT(Po)# 蝶形运算合并结果(使用逆单位根)y = [0] * nfor j in range(n // 2):y[j] = ye[j] + (omega ** j) * yo[j]y[j + n//2] = ye[j] - (omega ** j) * yo[j]return y
NTT:
FFT的缺点:
上面我们已经对FFT有了一定的了解,但是FFT存在一些问题就是里面用到了大量的三角函数和幂函数,导致运算时候的精度会有所损失,所以我们引入了新的算法NTT,其基本思想与FFT一致,但是在精度问题上大大减低1.复数表示
2.浮点数表示
所以我们解决这些缺点自然是想到:
复数表示–>实数表示
浮点数表示–>整数表示
前置数论知识:
欧拉函数ϕ(n)\phi(n)ϕ(n):
小于或等于n的正整数当中与n互质数的个数
费马小定理:
假设a为整数,p为质数,则ap=a(modp)a^p=a\quad (mod \quad p)ap=a(modp),若a,p互素的话,则ap−1=1(modp)a^{p-1}=1\quad (mod \quad p)ap−1=1(modp)
欧拉定理:
aϕ(n)=1(modn)a^{\phi(n)}=1 \quad (mod\quad n)aϕ(n)=1(modn)
阶:
满足同余式an=1(modm)a^n=1 (mod \quad m)an=1(modm)的最小正整数n存在,则这个n称为a模m的阶,记作:δm(a)\delta_m(a)δm(a)
假设 a=2, m=7
KaTeX parse error: {align*} can be used only in display mode.
因此当 ( a=2, m=7 ) 时阶数为3。(这里体现了一个==周期性!==即余数会以2,4,1循环)
原根:
设m∈N∗,a∈Zm\in \mathbb{N^*},a\in \mathbb{Z}m∈N∗,a∈Z。如果gcd(a,m)=1gcd(a,m)=1gcd(a,m)=1,且δm(a)=ϕ(m)\delta_m(a)=\phi(m)δm(a)=ϕ(m),则称a为模m的原根。如下图中的紫色部分
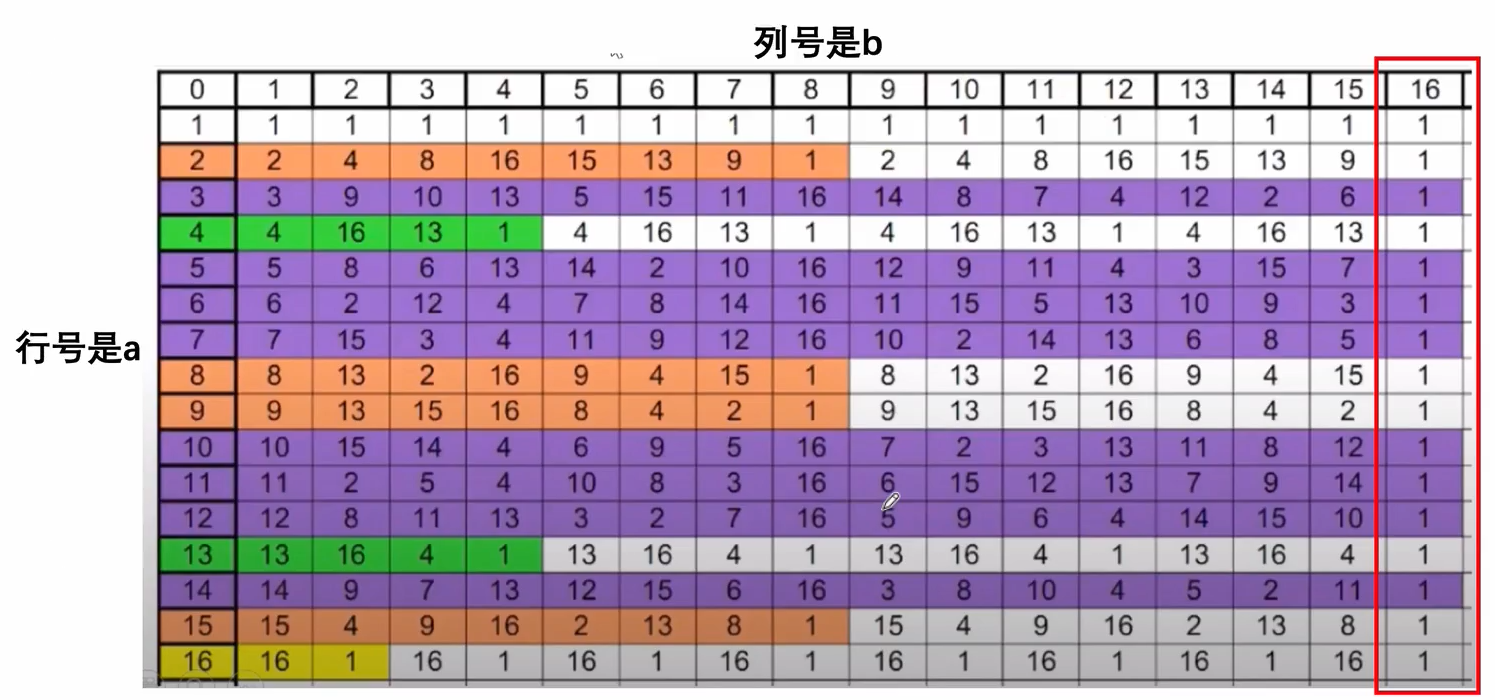
图注:abmod17a^b mod 17abmod17
NTT的核心思想
在有限域中用原根构造的单位根替代 FFT(快速傅里叶变换)中的单位复根,从而在整数模运算下实现多项式的高效卷积,避免复数运算带来的精度误差。
替代的原因有三:
本质是代数结构的 “同构替代”
FFT中:ωnk=e2πkin\omega^k_n = e^{\frac{2\pi k i}{n}}ωnk=en2πki
NTT中:gnk=(Gϕ(n)n)kmodpg_n^k = \left( G^{\frac{\phi(n)}{n}} \right)^k \mod pgnk=(Gnϕ(n))kmodp
其中G就是原根,是乘法群的生成元; gng_ngn是 n 次单位根:n 阶子群的生成元。
FFT中,单位复根ωnk=e2πikn\omega_n^k = e^{\frac{2\pi i k}{n}}ωnk=en2πik满足周期性:ωnk+n=ωnk\omega_n^{k + n} = \omega_n^kωnk+n=ωnk(周期为nnn)。
NTT中,构造的有限域单位根gng_ngn满足gnn≡1modpg_n^n \equiv 1 \mod pgnn≡1modp,因此gnk+n≡gnkmodpg_n^{k + n} \equiv g_n^k \mod pgnk+n≡gnkmodp,同样具有周期为nnn的周期性。
周期性是FFT/NTT“分治迭代”的基础(每一层的计算模式可重复)。
FFT中,在一个周期内(k=0,1,…,n−1k = 0,1,\dots,n-1k=0,1,…,n−1),ωnk\omega_n^kωnk的每个值互不相同(否则变换会丢失唯一性)。
NTT中,由于gng_ngn的阶为nnn(即gnk≡1modpg_n^k \equiv 1 \mod pgnk≡1modp当且仅当n∣kn \mid kn∣k),因此当k=0,1,…,n−1k = 0,1,\dots,n-1k=0,1,…,n−1时,gnkmodpg_n^k \mod pgnkmodp也互不相同。
这一性质保证了“不同位置的系数在变换中能被唯一区分”,是变换可逆性的前提。
FFT中,单位复根满足ωnk+n/2=−ωnk\omega_n^{k + n/2} = -\omega_n^kωnk+n/2=−ωnk(因eπi=−1e^{\pi i} = -1eπi=−1),这是“蝶形运算”中奇偶分离、符号翻转的核心依据。
NTT中,由于gnn≡1modpg_n^n \equiv 1 \mod pgnn≡1modp,故(gnn/2)2≡1modp(g_n^{n/2})^2 \equiv 1 \mod p(gnn/2)2≡1modp。又因为gng_ngn的阶为nnn(n/2<nn/2 < nn/2<n),所以gnn/2≢1modpg_n^{n/2} \not\equiv 1 \mod pgnn/2≡1modp,因此gnn/2≡−1modpg_n^{n/2} \equiv -1 \mod pgnn/2≡−1modp(有限域中,x2≡1modpx^2 \equiv 1 \mod px2≡1modp的非平凡解为x≡−1x \equiv -1x≡−1)。
由此可得:gnk+n/2=gnk⋅gnn/2≡−gnkmodpg_n^{k + n/2} = g_n^k \cdot g_n^{n/2} \equiv -g_n^k \mod pgnk+n/2=gnk⋅gnn/2≡−gnkmodp,与FFT的性质完全匹配,支持蝶形运算的符号逻辑。
具体例子(p=17,G=3,n=8p = 17, G = 3, n = 8p=17,G=3,n=8 时):
(317−18)kmod17\left( 3^{\frac{17 - 1}{8}} \right)^k \mod 17(3817−1)kmod17

NTT变换矩阵形式
[P(g0)P(g1)P(g2)⋮P(gn−1)]=[111…11gg2…gn−11g2g4…g2(n−1)⋮⋮⋮⋱⋮1gn−1g2(n−1)…g(n−1)(n−1)][p0p1p2⋮pn−1]modp\begin{bmatrix} P(g^0) \\ P(g^1) \\ P(g^2) \\ \vdots \\ P(g^{n-1}) \end{bmatrix} =\begin{bmatrix} 1 & 1 & 1 & \dots & 1 \\ 1 & g & g^2 & \dots & g^{n-1} \\ 1 & g^2 & g^4 & \dots & g^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & g^{n-1} & g^{2(n-1)} & \dots & g^{(n-1)(n-1)} \end{bmatrix} \begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ \vdots \\ p_{n-1} \end{bmatrix} \mod p P(g0)P(g1)P(g2)⋮P(gn−1)=111⋮11gg2⋮gn−11g2g4⋮g2(n−1)………⋱…1gn−1g2(n−1)⋮g(n−1)(n−1)p0p1p2⋮pn−1modp
其中:
- P(gk)P(g^k)P(gk) 表示多项式 P(x)=p0+p1x+p2x2+⋯+pn−1xn−1P(x) = p_0 + p_1 x + p_2 x^2 + \dots + p_{n-1} x^{n-1}P(x)=p0+p1x+p2x2+⋯+pn−1xn−1 在点 gkg^kgk 处的值(模 ppp)。
- 矩阵中的每个元素 gijg^{ij}gij 都计算模 ppp。
- 这个矩阵是一个范德蒙德矩阵(Vandermonde matrix),基于原根 ggg 的幂次。
逆NTT(INTT)变换矩阵形式
逆变换使用原根的逆元 g−1modpg^{-1} \mod pg−1modp 和一个缩放因子 n−1modpn^{-1} \mod pn−1modp(其中 n−1n^{-1}n−1 是 nnn 模 ppp 的乘法逆元)。INTT矩阵形式为:
[p0p1p2⋮pn−1]=n−1[111…11g−1g−2…g−(n−1)1g−2g−4…g−2(n−1)⋮⋮⋮⋱⋮1g−(n−1)g−2(n−1)…g−(n−1)(n−1)][P(g0)P(g1)P(g2)⋮P(gn−1)]modp\begin{bmatrix} p_0 \\ p_1 \\ p_2 \\ \vdots \\ p_{n-1} \end{bmatrix} = n^{-1} \begin{bmatrix} 1 & 1 & 1 & \dots & 1 \\ 1 & g^{-1} & g^{-2} & \dots & g^{-(n-1)} \\ 1 & g^{-2} & g^{-4} & \dots & g^{-2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & g^{-(n-1)} & g^{-2(n-1)} & \dots & g^{-(n-1)(n-1)} \end{bmatrix} \begin{bmatrix} P(g^0) \\ P(g^1) \\ P(g^2) \\ \vdots \\ P(g^{n-1}) \end{bmatrix} \mod p p0p1p2⋮pn−1=n−1111⋮11g−1g−2⋮g−(n−1)1g−2g−4⋮g−2(n−1)………⋱…1g−(n−1)g−2(n−1)⋮g−(n−1)(n−1)P(g0)P(g1)P(g2)⋮P(gn−1)modp
代码:
def NTT(P, g, p):"""数论变换:将系数表示的多项式转换为点值表示P: 系数列表 [p0, p1, ..., pn-1],n必须是2的幂g: 模p的原根(需满足n | p-1,即p ≡ 1 mod n)p: 模数(大质数,保证存在n次单位根)返回:点值列表 [P(ω^0), P(ω^1), ..., P(ω^{n-1})],其中ω是n次单位根"""n = len(P)if n == 1:return P # 递归基:长度为1时直接返回# 计算n次单位根:ω = g^((p-1)/n) mod pomega = pow_mod(g, (p - 1) // n, p)# 分治:奇偶分离Pe = P[::2] # 偶下标系数Po = P[1::2] # 奇下标系数ye = NTT(Pe, g, p)yo = NTT(Po, g, p)# 合并结果(蝶形运算)y = [0] * nfor j in range(n // 2):omega_j = pow_mod(omega, j, p) # ω^j mod py[j] = (ye[j] + omega_j * yo[j]) % py[j + n//2] = (ye[j] - omega_j * yo[j]) % preturn y
def INTT(P, g, p):"""逆数论变换:将点值表示转换为系数表示P: 点值列表 [P(ω^0), P(ω^1), ..., P(ω^{n-1})]g: 模p的原根(与NTT一致)p: 模数(与NTT一致)返回:系数列表 [p0, p1, ..., pn-1]"""n = len(P)if n == 1:return P # 递归基:长度为1时直接返回# 计算逆单位根:ω^(-1) = ω^(n-1) mod p(因ω^n ≡ 1)omega = pow_mod(g, (p - 1) // n, p)omega_inv = pow_mod(omega, n - 1, p) # ω的逆元# 分治:奇偶分离(与NTT对称)Pe = P[::2]Po = P[1::2]ye = INTT(Pe, g, p)yo = INTT(Po, g, p)# 合并结果(蝶形运算,使用逆单位根)y = [0] * nfor j in range(n // 2):omega_j = pow_mod(omega_inv, j, p) # (ω^(-1))^j mod py[j] = (ye[j] + omega_j * yo[j]) % py[j + n//2] = (ye[j] - omega_j * yo[j]) % p# 乘以n的模逆元(类似FFT中的1/n)n_inv = pow_mod(n, p - 2, p) # 费马小定理:n^(p-2) ≡ n^(-1) mod p(p是质数)for j in range(n):y[j] = (y[j] * n_inv) % preturn y
参考:快速傅里叶变换 - OI Wiki
快速傅里叶变换(FFT)——有史以来最巧妙的算法?_哔哩哔哩_bilibili,
硬核理解快速数论变换 Number-Theoretic Transform(NTT)_哔哩哔哩_bilibili
