递归，搜索与回溯算法

递归→搜索→回溯

名词解释

递归

1.什么是递归
形象地说就是函数自己调用自己。

例子：
二叉树的遍历-后序遍历

void dfs(treenode* root)
{//细节 - 出口if(root == NULL) return;dfs(root->left);dfs(root->right);printf(root->val);
}

快排

void quickSort(nums)
{// 基线条件：数组长度≤1时无需排序if 数组长度(arr) ≤ 1:return arr// 1. 选基准（此处选第一个元素）pivot = arr[0]// 2. 分两堆：小于等于基准的放left，大于基准的放rightleft = [所有 arr 中 ≤ pivot 的元素（除基准外）]right = [所有 arr 中 > pivot 的元素]// 3. 递归排序子数组，再合并结果return quickSort(left) + [pivot] + quickSort(right)
}

归并排序

void merge(nums, int left, int right)
{//细节 - 出口if(left >= right) return;int mid = (left +right)/2;merge(nums, left, mid);merge(nums, mid, right);合并两个有序数组
}

2.递归的本质
本质：
主问题—可以通过函数f分解—>相同的子问题
子问题—可以通过函数f分解—>相同的子问题
……
而分解主问题的函数，又可以继续用于以后的子问题，这样就形成了递归。

3.如何理解递归

1. 通过递归展开的细节图理解
2. 二叉树的题目
3. 宏观看待递归过程

• 不要过于在意递归的细节展开图
• 把递归的函数当成一个黑盒
• 相信黑盒一定能完成任务

4.如何写好一个递归
1.先找到相同的子问题。
2.只关心某一个子问题如何解决。
3.注意递归函数的出口。

搜索

1.深度优先遍历vs深度优先搜索（dfs： deep first search），宽度优先遍历vs宽度优先搜索（bfs：breath first search）
遍历是形式，搜索是目的。
dfs：深度优先搜索

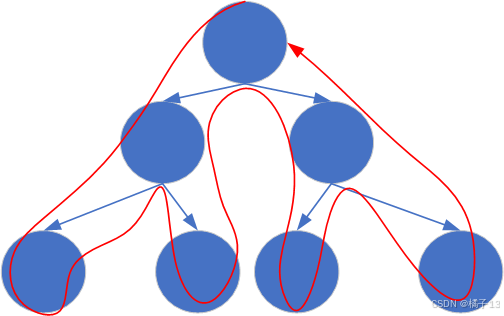
bfs：宽度优先搜索

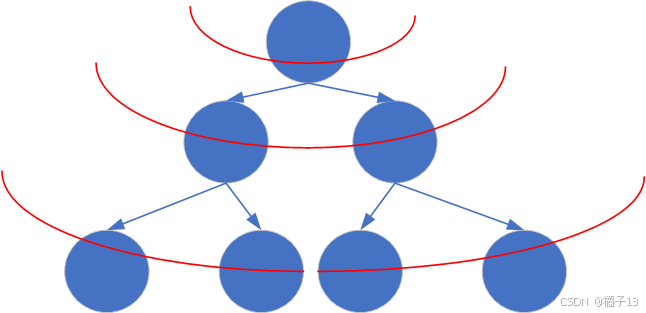
2.搜索vs暴力搜索
搜索=暴力搜索：遍历一遍所有的情况。
搜索（暴搜）两种方式：dfs（递归方式），bfs（优选方式）

3.拓展搜索问题
例子：全排列问题解决方式是树状图
例：1,2,3全排列

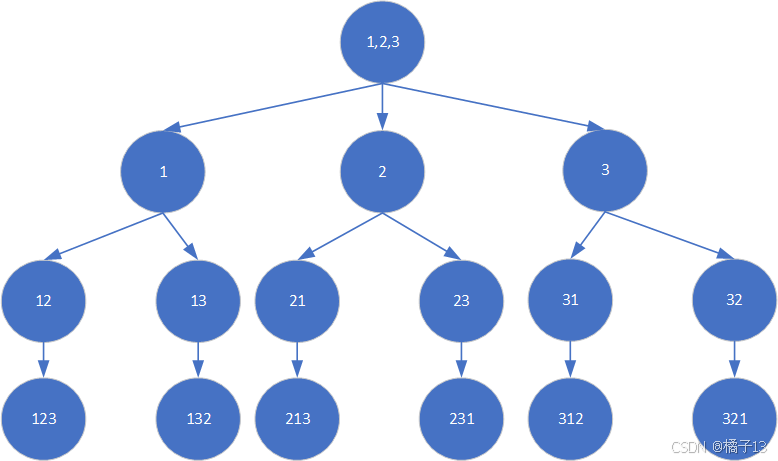
回溯与剪枝

1.本质
本质就是dfs。