当前位置：首页 > news >正文

08_多层感知机

news 2025/9/14 5:21:38

1. 单层感知机

1.1 感知机

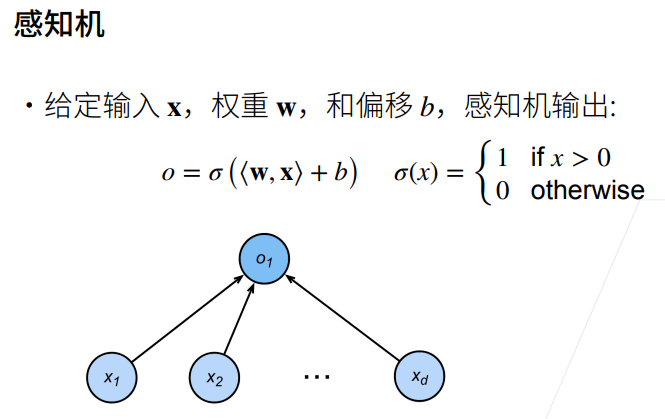
在这里插入图片描述

① 线性回归输出的是一个实数，感知机输出的是一个离散的类。

在这里插入图片描述

1.2 训练感知机

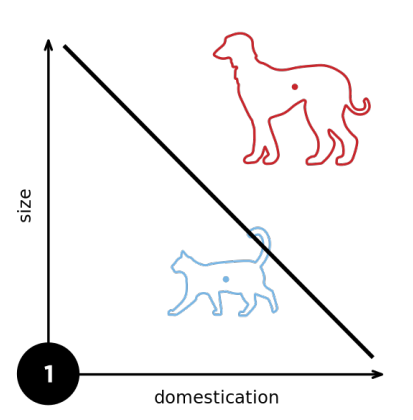
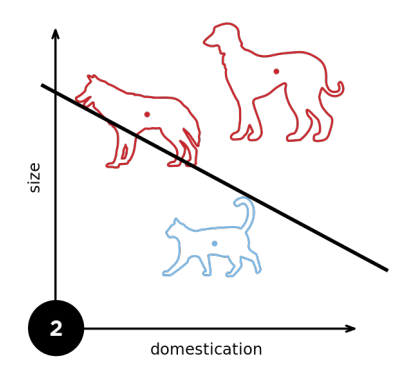
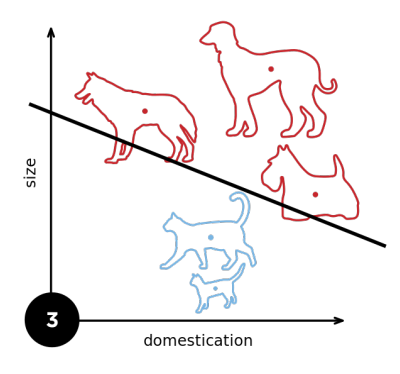
① 如果分类正确的话y<w,x>为正数，负号后变为一个负数，max后输出为0，则梯度不进行更新。

② 如果分类错了，y<w,x>为负数，下图中的if判断就成立了，就有梯度进行更新。

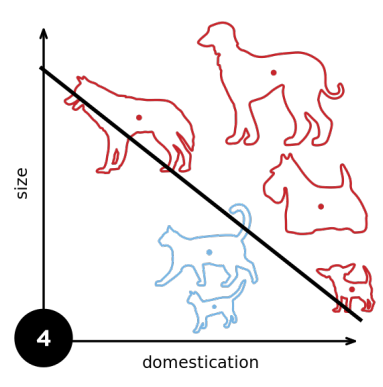
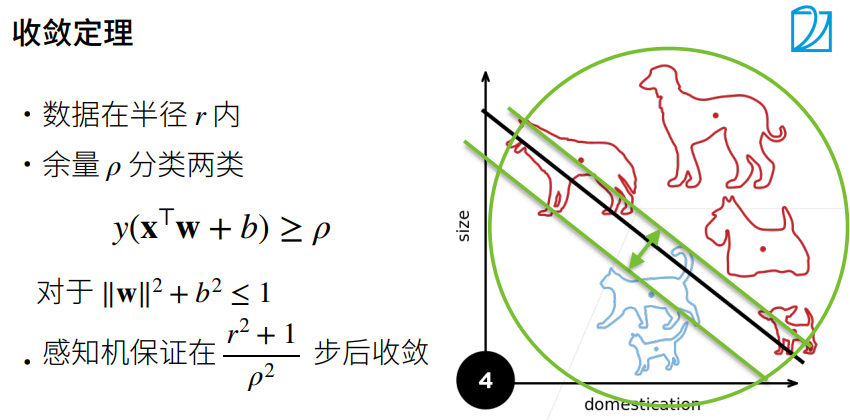
在这里插入图片描述

1.3 收敛半径

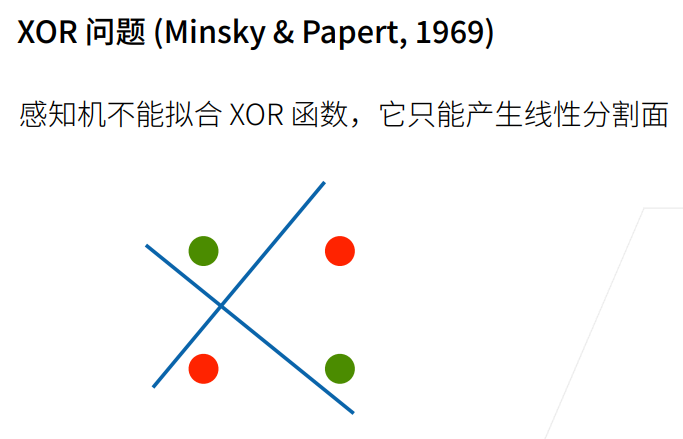
在这里插入图片描述

1.4 XOR问题

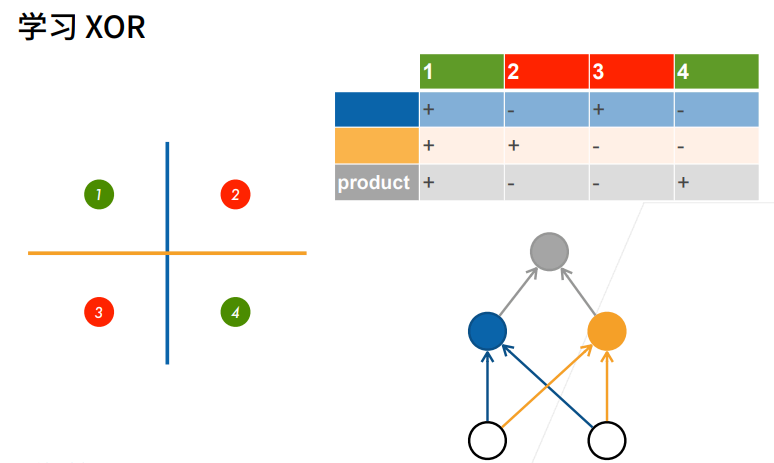
在这里插入图片描述

1.5 总结

在这里插入图片描述

2. 多层感知机

在这里插入图片描述

2.1 学习XOR

① 先用蓝色的线分，再用黄色的线分。

② 再对蓝色的线和黄色的线分出来的结果做乘法。

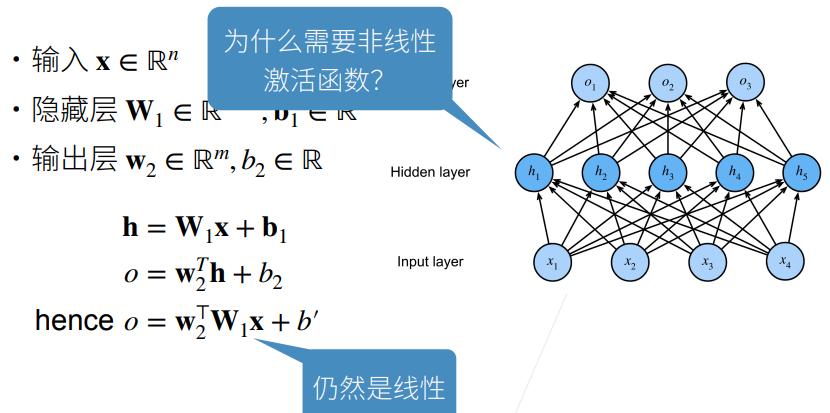
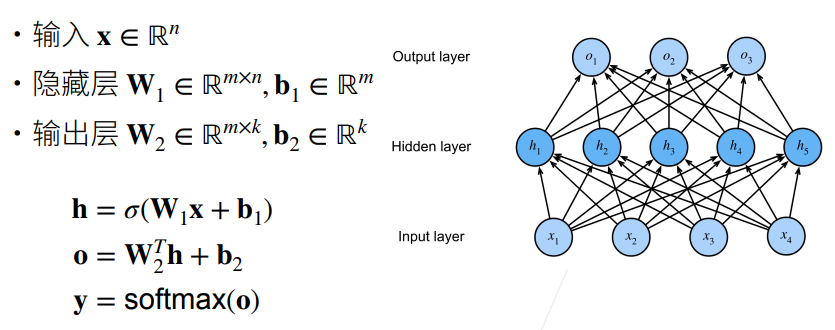
在这里插入图片描述

2.2 单隐藏层

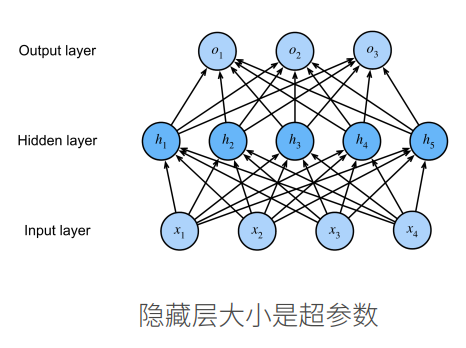
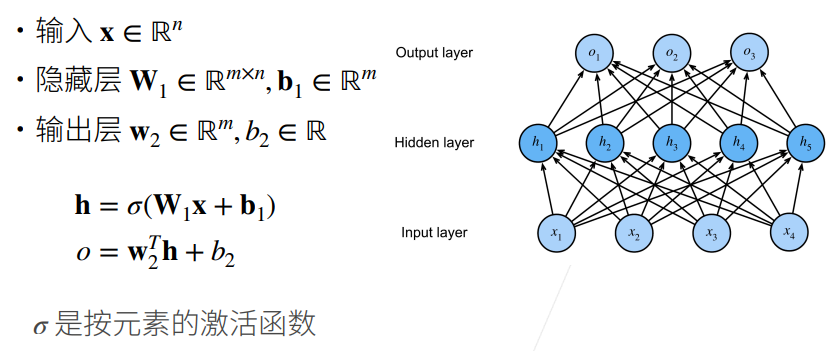
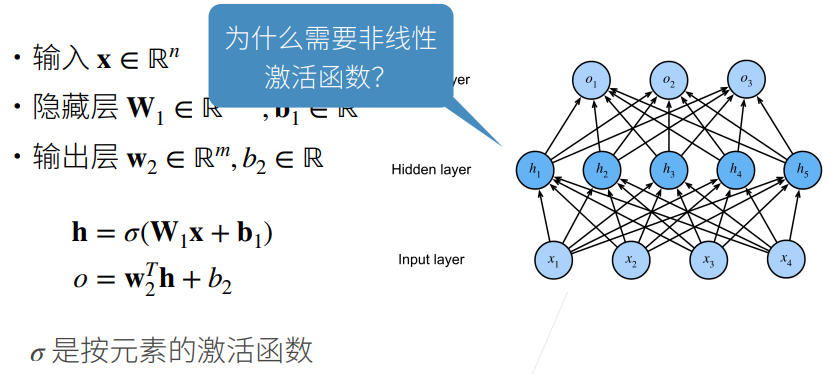
在这里插入图片描述

① 不用激活函数的话，所以全连接层连接在一起依旧可以用一个最简单的线性函数来表示。

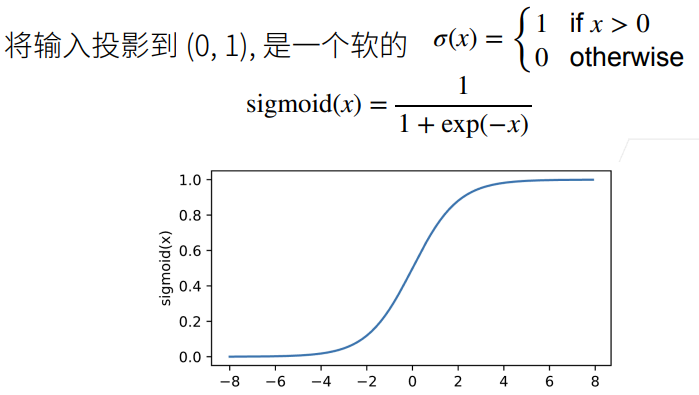
在这里插入图片描述

2.3 Sigmoid 函数

在这里插入图片描述

2.4 Tanh函数

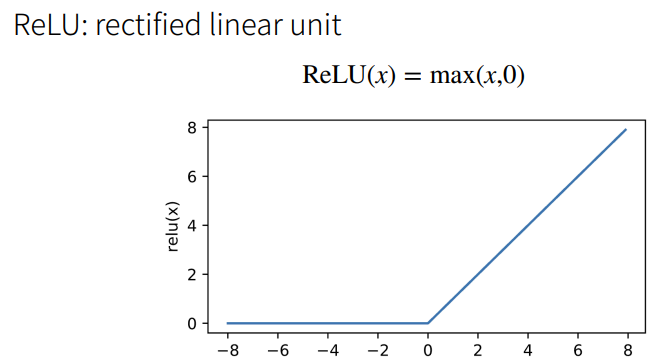
在这里插入图片描述

2.5 ReLU

① ReLU的好处在于不需要执行指数运算。

② 在CPU上一次指数运算相当于上百次乘法运算。

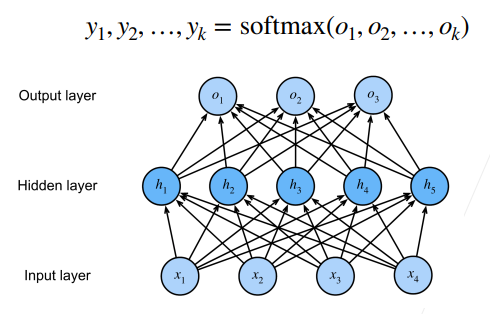
在这里插入图片描述

2.6 多类分类

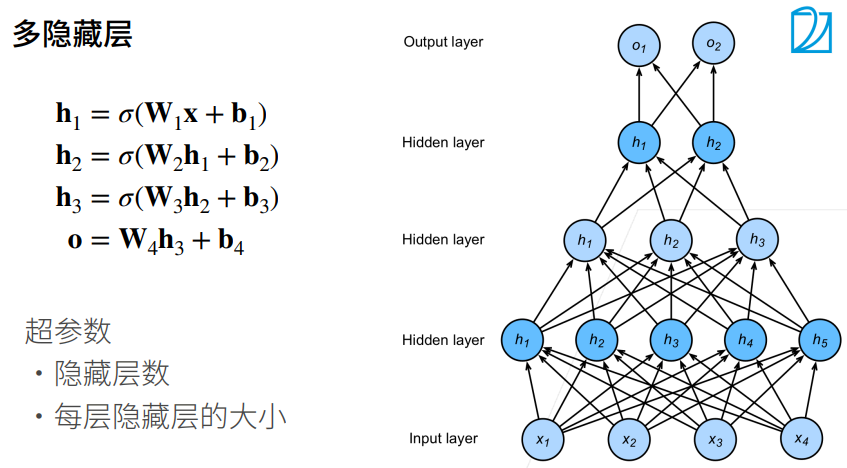
在这里插入图片描述

2.7 总结

在这里插入图片描述

1. 多层感知机（使用自定义）

import torch
from torch import nn
from d2l import torch as d2lbatch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)# 实现一个具有单隐藏层的多层感知机，它包含256个隐藏单元
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # 输入、输出是数据决定的，256是调参自己决定的
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1,b1,W2,b2]# 实现 ReLu 激活函数
def relu(X):a = torch.zeros_like(X) # 数据类型、形状都一样，但是值全为 0return torch.max(X,a)# 实现模型
def net(X):#print("X.shape:",X.shape)X = X.reshape((-1, num_inputs)) # -1为自适应的批量大小#print("X.shape:",X.shape)H = relu(X @ W1 + b1)#print("H.shape:",H.shape)#print("W2.shape:",W2.shape)return (H @ W2 + b2)# 损失
loss = nn.CrossEntropyLoss() # 交叉熵损失# 多层感知机的训练过程与softmax回归的训练过程完全一样
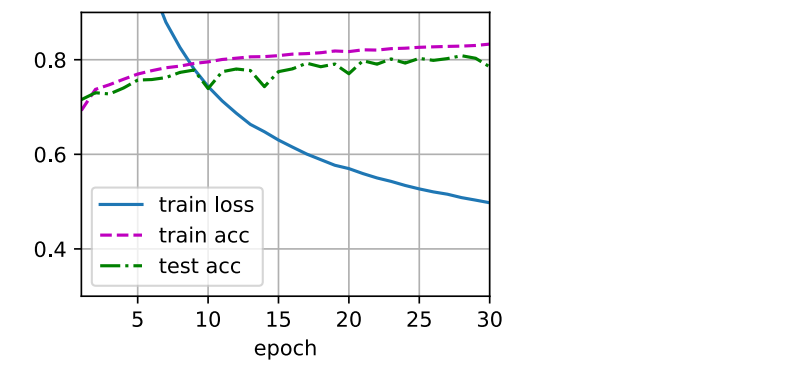
num_epochs ,lr = 30, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

在这里插入图片描述

2. 多层感知机（使用框架）

① 调用高级API更简洁地实现多层感知机。

import torch
from torch import nn
from d2l import torch as d2l# 隐藏层包含256个隐藏单元，并使用了ReLU激活函数
net = nn.Sequential(nn.Flatten(),nn.Linear(784,256),nn.ReLU(),nn.Linear(256,10))def init_weights(m):if type(m) == nn.Linear:nn.init.normal_(m.weight,std=0,)net.apply(init_weights)# 训练过程
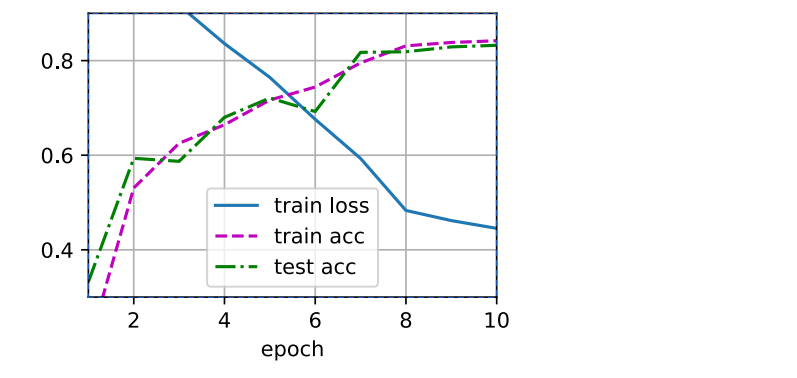
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

在这里插入图片描述

# 单层感知机函数
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l# 数据集
batch_size = 256
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size)# 初始化模型参数
num_inputs = 784
num_outputs = 10
num_hiddens = 256W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))params = [W1, b1]def relu(X):a = torch.zeros_like(X)return torch.max(X, a)# 定义网络
def net(X):X = X.reshape((-1, num_inputs))H = relu(X @ W1 + b1)return H# loss = nn.CrossEntropyLoss(reduction='none')
loss = nn.CrossEntropyLoss()num_epochs, lr = 10, 0.1
# updater = torch.optim.SGD(params, lr=lr)
updater = torch.optim.Adam(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

# 3层感知机函数
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l# 数据集
batch_size = 256
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size)# 初始化模型参数
num_inputs = 784
num_outputs = 10
num_hiddens1 = 256
num_hiddens2 = 128W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens1, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens1, num_hiddens2, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_hiddens2, requires_grad=True))
W3 = nn.Parameter(torch.randn(num_hiddens2, num_outputs, requires_grad=True) * 0.01)
b3 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))params = [W1, b1,W2,b2,W3,b3]def relu(X):a = torch.zeros_like(X)return torch.max(X, a)# 定义网络
def net(X):X = X.reshape((-1, num_inputs))H1 = relu(X @ W1 + b1)H2 = relu(H1 @ W2 + b2)return (H2 @ W3 + b3)# loss = nn.CrossEntropyLoss(reduction='none')
loss = nn.CrossEntropyLoss()
# 三层 学习率修改为0.01 效果会好一些
num_epochs, lr = 10, 0.01
# updater = torch.optim.SGD(params, lr=lr)
updater = torch.optim.Adam(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

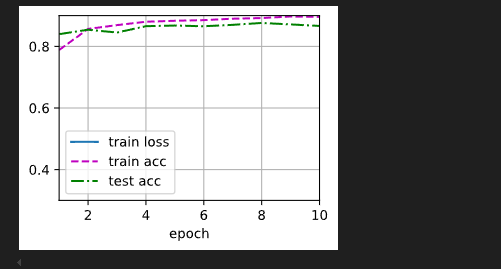
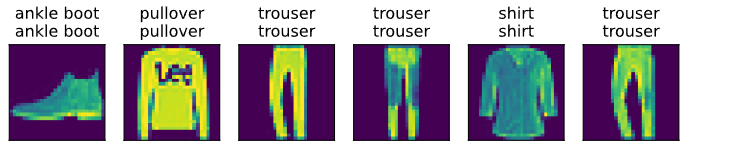
在这里插入图片描述

d2l.predict_ch3(net, test_iter)

在这里插入图片描述

感知机（Perceptron）简介

感知机（Perceptron）是最简单的神经网络模型之一，最早由 Frank Rosenblatt 在 1958 年提出。它是一个二分类模型，能够根据输入的特征，判断一个样本属于哪一类。尽管感知机本身非常简单，但它为后来的深度学习模型奠定了基础，尤其是多层感知机（MLP）和其他神经网络。

感知机是 线性分类器，意味着它只能对线性可分的任务进行有效的分类。对于无法用直线（或超平面）划分的任务，单层感知机是无法处理的，但通过将其扩展到多层神经网络，问题得到了很好的解决。

感知机的结构

感知机由以下几个部分组成：

输入层：感知机接受一个输入向量 $x=[x1,x2,...,xn]\mathbf{x} = [x_1, x_2, ..., x_n]$ ，表示样本的特征。
权重（Weights）：每个输入特征 $x_i$ 都有一个对应的权重 $w_i$ 。
偏置项（Bias）：为了使模型更具有表达能力，感知机还有一个偏置项 $b$ 。
激活函数：感知机通常使用一个阶跃函数（step function）作为激活函数，根据加权和与阈值的比较来决定输出。

感知机的数学表示

感知机的输出 $y$ 是通过以下步骤计算的：

加权和：

$\sum_{i=1}^{n} w_i x_i + b$

其中， $x_i$ 是输入特征， $w_i$ 是与 $x_i$ 对应的权重， $b$ 是偏置项。
激活函数（阶跃函数）：

$\begin{cases} 1 & \text{if } z \geq 0 \\ 0 & \text{if } z < 0 \end{cases}$

这里，阶跃函数（step function）会将加权和 $z$ 映射为一个二值输出 $y$ 。

感知机的推理过程

推理过程是指给定输入特征，感知机如何输出分类结果。其推理过程可以通过以下几个步骤来描述：

输入：将样本的特征 $x=[x1,x2,...,xn]\mathbf{x} = [x_1, x_2, ..., x_n]$ 输入到感知机中。
加权和计算：感知机首先计算输入特征和权重的加权和（即 $\sum_{i=1}^{n} w_i x_i + b$ ）。
激活函数应用：然后，感知机将加权和 $z$ 传递给阶跃激活函数，决定输出是 1 还是 0。
- 如果 $\geq 0$ ，则输出 1，表示样本属于一类。
- 如果 $z < 0$ ，则输出 0，表示样本属于另一类。
输出：感知机的最终输出 $y$ 是二值化的分类结果（0 或 1）。

感知机的推理示例

假设我们有以下输入特征 $x=[x1,x2]\mathbf{x} = [x_1, x_2]$ ，并且给定权重 $w=[w1,w2]\mathbf{w} = [w_1, w_2]$ 和偏置 $b$ ，感知机的输出通过以下步骤计算：

输入向量： $x=[x1,x2]=[1.0,2.0]\mathbf{x} = [x_1, x_2] = [1.0, 2.0]$
权重： $w=[w1,w2]=[0.5,0.5]\mathbf{w} = [w_1, w_2] = [0.5, 0.5]$
偏置项： $b = - 1.0$

首先，计算加权和 $z$ ：

$w_1 \cdot x_1 + w_2 \cdot x_2 + b = 0.5 \cdot 1.0 + 0.5 \cdot 2.0 - 1.0 = 0.5 + 1.0 - 1.0 = 0.5$

然后，使用阶跃激活函数对 $z$ 进行处理：

$\begin{cases} 1 & \text{if } z \geq 0 \\ 0 & \text{if } z < 0 \end{cases}$

由于 $\geq 0$ ，所以 $y = 1$ 。

感知机的训练过程

感知机的训练过程采用 感知机算法，该算法通过调整权重和偏置，使感知机的输出尽量接近实际目标。

初始化权重和偏置：权重和偏置通常被初始化为小的随机值。
预测输出：对于每个训练样本，计算感知机的预测输出。
计算误差：根据实际标签和预测输出之间的差异计算误差：

$\text{误差} = y_{\text{true}} - y_{\text{predicted}}$
权重更新：使用感知机学习规则来调整权重和偏置。如果预测错误，权重会根据误差进行调整。更新公式如下：

$w_i = w_i + \eta \cdot \text{误差} \cdot x_i$

$\eta \cdot \text{误差}$

其中 $η\eta$ 是学习率，控制更新的步长。
重复：通过迭代多个训练样本，直到误差为零或达到最大迭代次数。