关于线性子空间（Linear Subspace）的数学定义

1. 线性子空间（Linear Subspace）的数学定义

在数学上，一个向量空间 $V$ 的子集 $S$ 被称为线性子空间，当且仅当它满足以下三个条件：

1. 包含零向量：$0\in S$。这是最关键的一点，即必须包含原点。
2. 加法封闭性：如果 $\mathbf{u}\in S$ 且 $\mathbf{v}\in S$，那么 $\mathbf{u}+\mathbf{v}\in S$。
3. 数乘封闭性：如果 $\mathbf{u}\in S$ 且 $ c $ 是任意标量（实数或复数），那么 $c\mathbf{u}\in S$。

这三个条件是相互关联的。例如，由数乘封闭性可知，如果 $\mathbf{u}\in S$，那么 $0\cdot \mathbf{u}=0$ 也必须在 $S$ 中。因此，“包含原点”是线性子空间最基础、最本质的特性。

2. 几何直观理解

我们可以从几何角度来理解：

• 在二维空间 (${\mathbb{R}}^2$) 中：

  • 一个零维线性子空间：只有原点 $(0,0)$。
  • 一个一维线性子空间：一条穿过原点的直线。例如，直线 $y=2x$。这条直线上的任意两点相加，结果仍在该直线上；直线上任意一点乘以一个标量，结果也仍在该直线上。
  • 一个二维线性子空间：整个二维平面本身。
  • 反例：直线 $y=2x+1$ 不是一个线性子空间，因为它不经过原点。点 $(0,1)$ 和 $(1,3)$ 都在这条线上，但它们的和 $(1,4)$ 不在该直线上（因为 $4\ne 2\times 1+1$）。

• 在三维空间 (${\mathbb{R}}^3$) 中：

  • 一个零维线性子空间：原点 $(0,0,0)$。
  • 一个一维线性子空间：一条穿过原点的直线。
  • 一个二维线性子空间：一个穿过原点的平面。例如，X-Y平面 ($z=0$)。
  • 一个三维线性子空间：整个三维空间本身。
  • 反例：平面 $z=1$ 不是一个线性子空间，因为它平行于X-Y平面但不经过原点。点 $(0,0,1)$ 和 $(1,0,1)$ 都在这个平面上，但它们的和 $(1,0,2)$ 不在该平面上。

3. “数据样本精确地位于多个线性子空间的并集上”的含义

这句话描述了一种理想化的数据生成模型，是许多子空间聚类算法（如LRR、SSC）的理论基础。

• “位于…上”：意味着数据集中的每一个样本点 ${\mathbf{x}}_i$ 都可以被表示为它所属的那个线性子空间中其他点的线性组合。
  例如，如果样本 ${\mathbf{x}}_i$ 属于一个二维线性子空间（一个过原点的平面），那么它可以被该平面上任意两个不共线的基向量 ${\mathbf{v}}_1,{\mathbf{v}}_2$ 线性表示：${\mathbf{x}}_i=a_1{\mathbf{v}}_1+a_2{\mathbf{v}}_2$，其中 $a_1,a_2$ 是标量。

• “多个…的并集”：意味着整个数据集 X={x1,x2,...,xN}X = \{\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_N\}X={x1​,x2​,...,xN​} 并非全部位于一个单一的线性子空间内，而是分散在 $K$ 个不同的线性子空间 {S1,S2,...,SK}\{S_1, S_2, ..., S_K\}{S1​,S2​,...,SK​} 中。每个样本 ${\mathbf{x}}_i$ 只属于其中一个子空间 $S_k$。
  用集合论的语言，就是 $X\subseteq S_1\cup S_2\cup ...\cup S_K$。

• “精确地”：这是一个非常强的假设，意味着数据没有任何噪声或误差，每个点都完美地落在其所属的子空间内。

4. 为什么这个假设在现实中往往不成立？

正如论文中反复强调的，这个假设过于理想化，在现实世界中很难满足：

1. 数据噪声：真实采集的数据几乎总是包含噪声、遮挡、光照变化等干扰，导致样本点偏离其“真实”的子空间。
2. 仿射子空间更普遍：许多真实数据的结构更符合仿射子空间（Affine Subspace）模型。仿射子空间可以看作是线性子空间的一个“平移”。它不需要经过原点。
   • 例子1 (论文图1b)：在“Notting-Hill”人脸数据集中，不同人物的人脸图像可能形成不同的簇。这些簇（仿射子空间）在特征空间中可能表现为一些不经过原点的平面或直线。
   • 例子2：在运动分割中，一个刚体在视频帧中的运动轨迹点，通常位于一个仿射子空间中，而非必须经过原点的线性子空间。

5. 引入“必须包含原点”假设的后果

如果强行将本应属于仿射子空间的数据，用线性子空间模型来处理，会产生严重问题：

• 维度升高：为了用线性子空间表示一个 $d$ 维的仿射子空间，通常需要一个 $(d+1)$ 维的线性子空间（通过将原点“拉”进来）。这会人为地增加模型的复杂度。
• 子空间相交：不同仿射子空间在被强制转换为线性子空间后，它们更有可能在原点或其他地方相交。如论文图1b所示，两个本不相交的1D仿射子空间，在各自与原点构成2D线性子空间后，变成了同一个平面，完全无法区分。
• 破坏块对角结构：子空间学习的目标是学习一个块对角的自表示矩阵 $Z$，其中非零块对应于同一子空间内的样本。子空间的相交会直接破坏这种理想的块对角结构，导致聚类或分类性能下降。

总结来说，“数据样本精确地位于多个线性子空间的并集上”是一个核心但理想化的数学假设。其关键特性“必须包含原点”是为了满足线性代数中子空间的严格定义。然而，这个特性也成为了它的主要局限，因为它与许多现实世界数据的真实分布（仿射子空间）不符。这篇论文的核心贡献之一，就是通过引入仿射约束和非负约束，将模型从“线性子空间”推广到更普适、更贴近现实的“仿射子空间”，从而克服了这一根本性缺陷。

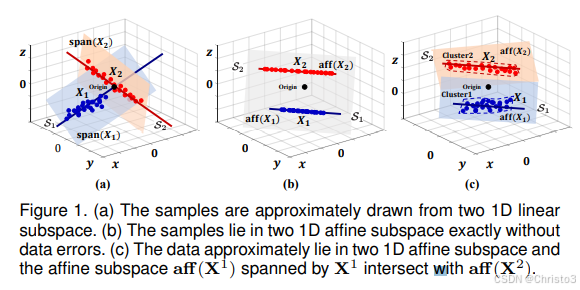
图1通过三个子图（a）、（b）、（c）清晰地展示了线性子空间（Linear Subspace）与仿射子空间（Affine Subspace）在数据建模上的根本差异，并揭示了传统方法（如LRR）的局限性以及本文提出的方法（ARLRR）的必要性。

整体理解

这张图的核心目的是说明：现实世界的数据更符合“仿射子空间”的分布模型，而非理想的“线性子空间”模型。 传统的低秩表示（LRR）方法假设数据位于线性子空间上，但这种假设在存在噪声或数据本身不经过原点时会失效，导致聚类性能下降。本文提出的“仿射约束”和“非负约束”正是为了解决这个问题。

---

逐个子图解析

(a) 图：理想化的线性子空间 (Ideal Linear Subspaces)

• 场景描述：该图展示了一个最理想的情况。两个数据簇 $X_1$ 和 $X_2$ 近似地分布在两条一维线性子空间（1D Linear Subspaces）上。
• 关键特征：
  • 过原点：这两条直线都精确地穿过坐标系的原点 (Origin)。这是线性子空间的定义性特征。任何线性子空间必须包含零向量（即原点）。
  • 符号解释：span(X₁) 和 span(X₂) 表示由数据集 $X_1$ 和 $X_2$ 张成的线性子空间。在这里，它们就是那两条红色的直线。
  • 问题所在：虽然这个模型很完美，但它是一个理想化假设。现实中，数据几乎总是包含噪声（data errors），并且数据簇的中心通常不会恰好在原点。因此，这个模型在真实应用中往往不成立。

(b) 图：精确的仿射子空间 (Exact Affine Subspaces)

• 场景描述：此图展示了一个更真实的场景。两个数据簇 $X_1$ 和 $X_2$ 精确地分布在两条一维仿射子空间（1D Affine Subspaces）上，且没有数据错误。
• 关键特征：
  • 不过原点：这两条直线都不经过原点。这正是“仿射子空间”的本质。一个仿射子空间可以看作是一个线性子空间平移（translate）后的结果。
  • 符号解释：aff(X₁) 和 aff(X₂) 分别表示由数据集 $X_1$ 和 $X_2$ 张成的仿射子空间。它们是两条平行于某个过原点的直线，但位置不同的直线。
  • 问题暴露：尽管没有噪声，但当我们将这些数据输入到传统的LRR等方法时，会发生什么？LRR会尝试寻找一个能包含所有数据的最小线性子空间。由于 $X_1$ 和 $X_2$ 都不经过原点，LRR会找到一个包含这两个仿射子空间和原点的更大的线性子空间。例如，它可能会找到一个二维平面来包含这两条直线。这就导致了子空间相交的问题。原本应该被分到不同簇的样本，在这个二维平面中可能变得非常接近，破坏了理想的“块对角结构”（Block Diagonal Property, BDP），使得聚类变得困难。

© 图：近似的仿射子空间且存在相交 (Approximate Affine Subspaces with Intersection)

• 场景描述：这是最贴近现实世界的一个例子。数据近似地分布在两个一维仿射子空间上，但存在数据错误（data errors），并且这两个仿射子空间相互交叉。
• 关键特征：
  • 近似分布：数据点 $X_1$ 和 $X_2$ 并不完全严格地落在一条直线上，而是围绕着各自的直线有轻微的散落，这代表了噪声或测量误差。
  • 子空间相交：图中明确标出了 aff(X¹) 和 aff(X²) 两个仿射子空间发生了相交。这可能是由于数据本身的复杂性或噪声导致的。
  • 后果严重：当两个子空间相交时，那些位于交点附近的样本就处于“两难境地”。它们既靠近 $X_1$ 的簇，也靠近 $X_2$ 的簇。传统的LRR方法在这种情况下会完全失效，因为它无法区分这些样本属于哪个簇，从而导致严重的聚类错误。

总结与核心洞见

综合这三个子图，我们可以得出以下结论：

1. 线性子空间模型的局限性：图(a)的理想情况在现实中很少出现。图(b)和©表明，数据更常分布在仿射子空间上。
2. 仿射子空间的挑战：即使数据分布在仿射子空间上，传统方法（如LRR）也会因为其固有的“过原点”假设而失败。它会将多个仿射子空间“拉”到一个更高的维度上，造成不必要的相交（如图b所示），或者直接处理不了复杂的相交情况（如图c所示）。
3. 本文的解决方案：本文提出的“仿射约束” (1^T Z = 1^T) 保证了自表示矩阵 $Z$ 的每一列和为1，这从数学上确保了每个样本只能用其所在仿射子空间内的其他样本进行仿射组合来表示。这解决了“过原点”的问题。
4. 非负约束的增强作用：在此基础上增加“非负约束” (0 ≤ Z_{ij} ≤ 1)，进一步将这种组合限制为凸组合（Convex Combination）。这不仅加强了仿射约束，还引入了局部几何信息，使得模型能够更好地利用数据在子空间内的局部分布结构（如凸包），从而在面对噪声和子空间相交的情况下，依然能学习到一个具有块对角结构的、鲁棒的自表示矩阵。

总而言之，图1生动地证明了为什么需要从“线性子空间”转向“仿射子空间”建模，并为本文提出的“仿射+非负”双重约束提供了直观的几何解释。

＃＃　块对角性质（Block Diagonal Property, BDP）。

这个定义是理解整个子空间聚类（Subspace Clustering）任务成功与否的核心。它描述了理想情况下，自表示矩阵 $Z$ 应该具有的结构。

1. 核心概念：块对角矩阵

想象一下一个大的 $N\times N$ 的方阵 $Z$。如果这个矩阵的非零元素只集中在沿着主对角线分布的几个“块”中，而这些块之间的区域都是零，那么这个矩阵就被称为块对角矩阵。

• 形式化表示：
  $$Z=\left[\begin{array}{cccc}{Z}^1& 0& \cdots & 0\\ 0& Z^2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & Z^K\end{array}\right]$$
  这里，$Z^k$ 是一个 $N_k\times N_k$ 的子矩阵，对应于第 $k$ 个子空间内的样本。

• 直观理解：

  • 矩阵 $Z$ 的每一列 $z_j$ 表示样本 $x_j$ 如何被其他所有样本 $x_i$（$i=1,2,...,N$）进行线性组合来重构。
  • 如果 $Z$ 具有块对角性质，就意味着：来自同一个子空间 $S_k$ 的样本 $x_j$，只能用同样来自 $S_k$ 的其他样本 $x_i$ 来重构，而不能用来自其他子空间 $S_{\ell }$ ($\ell \ne k$) 的样本来重构。
  • 例如，如果 $x_3$ 和 $x_5$ 都属于子空间 $S_1$，那么在 $Z$ 的第3列 $z_3$ 中，只有 $z_{3,5}$ 可能是非零的（表示 $x_3$ 被 $x_5$ 重构），而 $z_{3,7}$ 必须为零（因为 $x_7$ 属于另一个子空间 $S_2$，不能用于重构 $x_3$）。

2. 定义解析与关键点

让我们逐句分析定义：

• “Given a data matrix $X=[X^1,X^2,...,X^K]\in {\mathbb{R}}^{d\times N}$ drawn from a union of K subspaces…”

  • 这句话说明数据 $X$ 包含了 $N$ 个样本，这些样本分布在 $K$ 个不同的低维子空间上。
  • $X^k\in {\mathbb{R}}^{d\times N_k}$ 是一个子矩阵，包含了属于第 $k$ 个子空间的所有 $N_k$ 个样本。

• “…we say that $Z$ obeys the block diagonal property if $Z$ is K-block diagonal as follows:…”

  • 这是核心断言：我们希望自表示矩阵 $Z$ 具有这种理想的块对角结构。

• “where the nonzero entries $Z^k$ correspond to only $X^k$.”

  • 这是对块对角结构的补充说明。它强调了每个非零块 $Z^k$ 内部的系数，只与属于同一子空间 $X^k$ 的样本相关联。

3. 为什么块对角性质如此重要？

BDP 是子空间聚类成功的“圣杯”。它的意义在于：

1. 直接揭示聚类结果：一旦我们得到了一个具有 BDP 的 $Z$ 矩阵，聚类结果就一目了然。我们可以直接根据 $Z$ 的块结构，将样本分组到对应的子空间中。
2. 理论保证：许多经典的子空间聚类算法（如LRR、SSC）都建立在这样的理论基础上：如果数据是完美的（无噪声）、且子空间是线性独立的，那么通过求解其优化问题，得到的最优解 $Z$ 就会自动满足 BDP。
3. 实现聚类的桥梁：获得 $Z$ 后，通常会将其转换成一个相似度图（Affinity Graph）。对于 BDP 的 $Z$，这个图的连接关系非常清晰：同簇内的样本之间有强连接，不同簇间的样本之间没有连接。然后，应用谱聚类（Spectral Clustering）等方法，就能轻松地将样本分割成正确的簇。

4. 论文中的挑战：为何 BDP 很难保证？

正如论文在引言和图1中所阐述的，现实世界的数据往往不满足完美BPD所需的严格条件，这导致了传统方法的失效：

1. 数据误差 (Data Errors)：真实数据总是包含噪声、遮挡或测量误差。这些误差会导致样本点偏离其真实的子空间，使得它们的张成空间维度升高，从而可能与其他子空间产生交集。当两个子空间相交时，位于交集处的样本可以被来自不同子空间的点共同表示，破坏了BDP。
2. 仿射子空间 (Affine Subspaces)：如图1(b)所示，许多真实数据（如人脸、运动轨迹）更符合仿射子空间模型，即子空间不经过原点。传统的LRR假设数据在线性子空间上，但为了处理仿射子空间，LRR会将它们“拉”到一个更高维度的线性子空间中（必须包含原点），这增加了子空间相交的可能性，从而破坏了BDP。

5. 本文的解决方案：如何恢复 BDP？

这篇论文的核心贡献就是提出了一种新的方法，通过引入约束来强制模型学习一个近似满足BDP的 $Z$ 矩阵。

• 仿射约束 (1^T Z = 1^T)：确保每个样本 $x_j$ 的重构是其所在子空间内其他样本的仿射组合（Affine Combination），这允许处理仿射子空间。
• 非负约束 (0 ≤ Z_ij ≤ 1)：结合仿射约束，这使得 $x_j$ 的重构成为其所在子空间内其他样本的凸组合（Convex Combination）。

这两个约束的联合效果是：它迫使模型去寻找一种表示，使得每个样本尽可能地由其“邻居”（同簇内样本）进行重构，从而显式地利用了局部聚类结构信息。这种局部信息有助于模型在存在噪声和仿射结构的情况下，仍然能够学习到一个接近块对角的 $Z$ 矩阵，最终实现鲁棒的聚类。

总结来说， Definition 1 定义了子空间聚类的理想目标——块对角矩阵 $Z$。它是一个强有力的几何先验，意味着“同类样本只用同类样本来表示”。论文通过引入仿射和非负约束，旨在克服现实数据带来的挑战（噪声、仿射结构），从而逼近这一理想状态，这是其方法有效性的根本原因。