MATLAB基于博弈论-云模型的城市道路塌陷风险评价模型
基于博弈论-云模型的城市道路塌陷风险评价模型
1. 模型核心思想
该模型的核心在于优势互补:
- 博弈论:用于解决由层次分析法(AHP)确定的主观权重与由熵权法(EWM)确定的客观权重之间的冲突,寻求二者之间的“纳什均衡”,得到综合最优的组合权重。这避免了单一赋权法的片面性。
- 云模型:由李德毅院士提出,是一种用于处理定性概念与定量描述间不确定转换的模型,特别擅长处理模糊性(事物概念的不明确性)和随机性(概率分配的不确定性)。它通过期望(Ex)、熵(En)、超熵(He) 三个数字特征来定义一个概念,完美契合风险评价中“高风险”、“中风险”等语言值的特性。
流程简图:
风险指标体系建立 → 博弈论组合赋权 (AHP主观权重 + 熵权法客观权重) → 确定综合权重 → 云模型风险评价 (构建标准云、确定评估云、计算确定度) → 风险等级判定
2. 模型构建步骤
步骤一:建立城市道路塌陷风险评价指标体系 (U)
从系统论出发,从致灾因子、承灾体、孕灾环境等多维度筛选评价指标,构建一个多层次、多指标的评价体系。
- 目标层 (A):城市道路塌陷风险等级
- 准则层 (B) (示例):
- B1: 地质与管线条件:岩土体类型、地下水位、管线老化程度、管线渗漏隐患等。
- B2: 道路结构与荷载:道路年龄、路基质量、日均车流量、重载车辆比例等。
- B3: 环境与气候因素:年均降水量、极端降雨频率、周边施工活动强度、振动源等。
- B4: 监测与维护水平:巡检频率、探测技术应用、历史病害处置率等。
- 指标层 ©:为每个准则层细化具体的、可量化的评估指标。例如,
C11: 管线年龄(年),C12: 土体疏松程度(定性分级量化)等。
步骤二:基于博弈论的组合赋权
1. 主观权重 (ω1) - AHP法
- 邀请专家对同一层级内的指标进行两两比较,构建判断矩阵。
- 计算矩阵的特征向量,得到权重ω1,并进行一致性检验(CR<0.1)。
2. 客观权重 (ω2) - 熵权法
- 收集各评价指标在多个评价路段或历史时间点的原始数据,形成初始矩阵。
- 对数据进行标准化处理(消除量纲)。
- 计算各指标的信息熵,熵值越小,说明指标数据差异越大,其权重应越大。据此计算客观权重ω2。
3. 博弈论组合权重 (ω)*
- 将两种权重向量视为两个决策主体在进行博弈,目标是找到一组最稳定的权重,使得它与两种权重的一致性偏差最小。

步骤三:基于云模型的风险等级评价
1. 划分风险等级并构建标准云
- 将风险划分为5个等级(例如:低风险、较低风险、中风险、较高风险、高风险)。
- 为每个等级划分论域(数值范围),通常设定在[0,1]或[0,100]之间。
- 利用逆向云发生器,根据每个等级的数值区间,生成对应每个风险等级的标准云模型(Ex, En, He)。
- 期望Ex:区间的中心值,代表该等级最典型的值。
- 熵En:代表概念的模糊程度,通常
En = (区间上限 - 区间下限) / c,c为常数(通常取2.355或2.447,取决于99%或95%的隶属度覆盖区间)。 - 超熵He:代表熵的不确定性,即云的厚度,通常根据经验设定一个较小值。
2. 确定待评对象的评估云
- 收集待评价道路路段各指标C的实际数据X = (x1, x2, …, xn)。
- 结合步骤二得到的综合权重ω*,计算该路段的综合得分(或采用加权平均法)。
- 注意:需先将指标数据进行归一化,使所有指标处于同一量纲。
3. 计算确定度
- 将待评路段的综合得分作为输入,代入X条件云发生器。
- 计算该得分相对于每一个风险等级标准云的确定度(隶属度)μ。
- 生成一个以
En为期望,He为标准差的正态随机数En'。 - 计算确定度:
[
\mu = \exp{\left[ -\frac{(x - Ex)2}{2(En’)2} \right]}
]
- 生成一个以
- 为提高精度,此过程可重复N次(如1000次),取μ的平均值作为最终对该等级的确定度。
4. 评定风险等级
- 遵循最大确定度原则。比较待评路段相对于5个标准云的确定度,其归属的风险等级为确定度最大的那个等级。
Risk_Level = argmax(μ_i), 其中i=1,2,3,4,5
3. 模型优势与特点
- 科学赋权:博弈论组合赋权克服了单一赋权法的缺陷,使权重分配既符合主观认知,又尊重客观数据规律,结果更合理。
- 处理不确定性:云模型不仅能处理风险的模糊性(如“风险较高”这个概念本身是模糊的),还能处理其随机性(如测量误差、数据波动),评价结果更贴近现实。
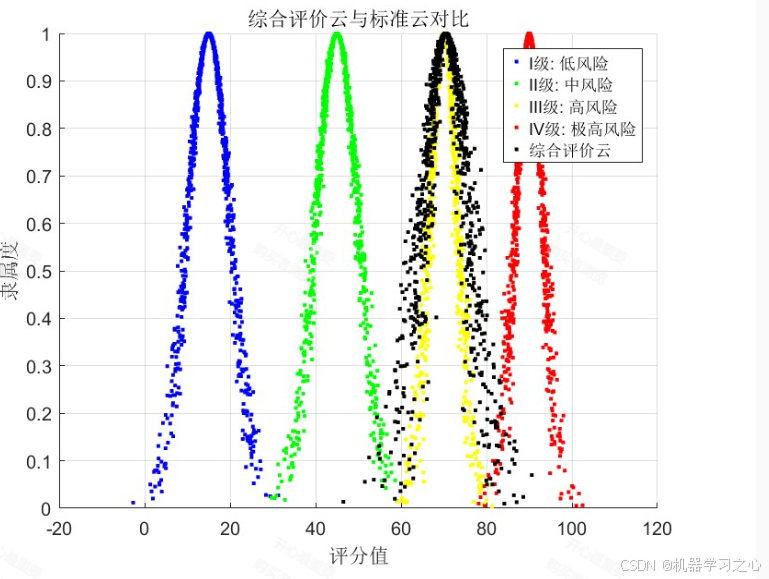
- 可视化强:云模型生成的风险等级云图非常直观,可以清晰地看到待评对象位于哪个等级的“云团”中,以及它介于两个等级之间的过渡状态。
- 精度高:通过多次计算取平均确定度,降低了随机性干扰,提高了评价结果的稳定性。
4. 应用示例(简化的概念性说明)
假设评价某路段“地质与管线条件(B1)”的风险。
- 指标:管线年龄(C11)、土体类型(C12)。
- 组合权重:ω*(C11)=0.6, ω*(C12)=0.4。
- 数据:该路段管线年龄50年(归一化后得分0.8),土体为疏松砂土(归一化后得分0.9)。
- 综合得分:
S = 0.6*0.8 + 0.4*0.9 = 0.84。 - 云评价:将0.84输入X条件云发生器,计算它相对于5个风险等级标准云的确定度。假设得到对“高风险”云的确定度最高(μ=0.75),则该路段B1准则层风险等级为“高风险”。
最后,可逐层向上聚合,得到该路段的最终整体风险等级。
5. 总结
该模型融合了博弈论和云模型的优点,为城市道路塌陷风险评价提供了一种兼顾主客观信息、有效处理不确定性、结果科学可靠的新方法。它不仅能够给出确定的风险等级,还能以“云”的形式展示评价过程中的不确定性,为城市基础设施的安全管理和风险预警提供更精细、更科学的决策支持。