112. 路径总和
目录
题目链接:
题目:
解题思路:
代码:
递归法
迭代法
总结:
题目链接:
112. 路径总和 - 力扣(LeetCode)
题目:
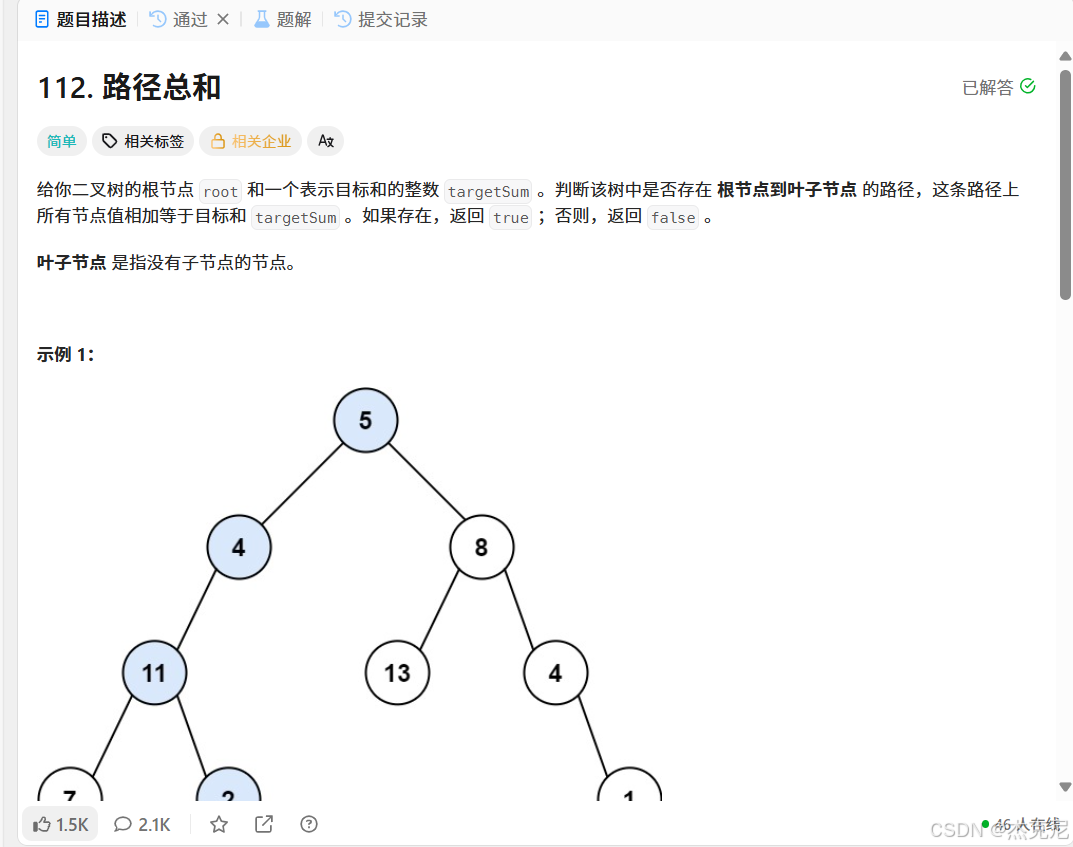
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
解题思路:
递归回溯法:使用前序遍历,(树的递归何时需要返回值,如果是找一条路径,需要返回值;如果是需要处理整颗树且不用处理返回值,则不需要),判断条件是遇到节点恰好值为目标值即可返回true;
迭代法也是可以的,但是需要俩栈,一个存储当前节点,一直存储当前值,判断是否需要返回
代码:
递归法
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if(root==null){return false;}return find(root,targetSum); }public boolean find(TreeNode root,int sum){if(root==null) return false;sum-=root.val;if(root.left==null&&root.right==null){return sum==0;}if(root.left!=null){boolean left=find(root.left,sum);if(left==true){return true;}}if(root.right!=null){boolean right=find(root.right,sum);if(right==true){return true;}}return false;}
}二叉树路径总和判断算法解析:深度优先搜索的递归实现
在二叉树的算法问题中,判断是否是否存在一条从根节点到叶子节点的路径,使得路径上所有节点值之和等于目标值,是一道经典的基础题目。这道题不仅考察了对二叉树结构的理解,也考验了递归遍历算法的应用。本文将详细解析一段基于深度优先搜索(DFS)的递归实现代码,从问题分析到代码执行流程,全面剖析这一问题的解决方案。
问题背景与定义解析
首先,我们需要明确问题的定义:
给定一棵二叉树和一个目标和targetSum
判断该树中是否存在一条从根节点到叶子节点的路径
路径上所有节点的值相加等于targetSum
叶子节点是指没有左子树和右子树的节点(即left == null && right == null)
例如,在下面的二叉树中,目标和为 22:
plaintext
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
存在一条路径5->4->11->2,节点值之和为 5+4+11+2=22,因此算法应返回true。
理解 "从根到叶子" 这一条件至关重要,很多初学者会误将任意路径(如非叶子节点结束的路径)考虑在内,这是需要特别注意的。
代码整体结构分析
这段代码采用递归深度优先搜索的思路,通过两个方法协作完成判断:
java
运行
class Solution {
// 主方法:判断是否存在符合条件的路径
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root==null){
return false;
}
return find(root,targetSum);
}
// 辅助递归方法:搜索路径
public boolean find(TreeNode root,int sum){
// 递归终止条件
if(root==null) return false;
// 减去当前节点值
sum -= root.val;
// 判断是否为叶子节点且sum已减为0
if(root.left==null&&root.right==null){
return sum==0;
}
// 递归搜索左子树
if(root.left!=null){
boolean left=find(root.left,sum);
if(left==true){
return true;
}
}
// 递归搜索右子树
if(root.right!=null){
boolean right=find(root.right,sum);
if(right==true){
return true;
}
}
// 左右子树都没有符合条件的路径
return false;
}
}
代码的整体结构遵循了 "主方法 + 辅助递归方法" 的模式:
主方法hasPathSum负责处理空树的边界情况,并启动递归搜索
辅助方法find实现核心的递归逻辑,包括:
递归终止条件判断
当前节点值处理
叶子节点判断与目标和校验
左子树和右子树的递归搜索
结果合并与返回
这种结构将边界处理与核心逻辑分离,使代码更清晰易读。
核心代码逐行解析
1. 主方法:边界条件处理
java
运行
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root==null){
return false;
}
return find(root,targetSum);
}
主方法的逻辑非常简洁:
首先判断根节点是否为null(空树),如果是,直接返回false,因为空树不可能有任何路径
如果根节点不为null,调用辅助方法find开始递归搜索,传入根节点和目标和
这一步处理了空树的特殊情况,避免了后续递归中可能出现的空指针异常。
2. 辅助方法:递归终止条件
java
运行
public boolean find(TreeNode root,int sum){
if(root==null) return false;
// ... 其他逻辑
}
这是递归的基本终止条件:当传入的节点为null时,返回false。这意味着当前路径无法继续延伸到有效节点,自然不可能形成符合条件的路径。
3. 当前节点值处理
java
运行
sum -= root.val;
这行代码是算法的核心操作之一:将当前节点的值从剩余和中减去。通过这种方式,我们追踪从根节点到当前节点的路径上已累积的节点值之和。当到达叶子节点时,如果剩余的sum为 0,说明这条路径的总和等于初始的目标和。
这种 "减法" 思路比 "加法" 思路(累加路径和再与目标和比较)更简洁,避免了额外的累加变量。
4. 叶子节点判断与结果校验
java
运行
if(root.left==null&&root.right==null){
return sum==0;
}
这是判断路径是否有效的关键条件:
首先检查当前节点是否为叶子节点(左右子节点都为null)
如果是叶子节点,检查经过该节点后剩余的sum是否为 0
如果sum == 0,返回true(找到符合条件的路径)
否则,返回false(该路径不符合条件)
这一步确保了只有 "从根到叶子" 的完整路径才会被考虑,符合问题的定义。
5. 左子树递归搜索
java
运行
if(root.left!=null){
boolean left=find(root.left,sum);
if(left==true){
return true;
}
}
这段代码处理左子树的递归搜索:
首先检查左子节点是否存在(root.left != null)
如果存在,递归调用find方法搜索左子树,传入左子节点和当前剩余的sum
接收递归返回的结果,如果为true(左子树中存在符合条件的路径),立即返回true
这种 "短路" 处理非常高效,一旦找到一条符合条件的路径,就可以立即返回,无需继续搜索其他路径。
6. 右子树递归搜索
java
运行
if(root.right!=null){
boolean right=find(root.right,sum);
if(right==true){
return true;
}
}
这段代码与左子树处理逻辑类似:
检查右子节点是否存在
递归搜索右子树
如果找到符合条件的路径,立即返回true
注意这里先搜索左子树,再搜索右子树,体现了深度优先搜索的特点。
7. 无符合条件路径的返回
java
运行
return false;
如果当前节点的左右子树都搜索完毕且没有找到符合条件的路径,返回false,表示从当前节点出发的所有路径都不符合条件。
算法执行流程示例
为了更直观地理解算法的执行过程,我们以上面提到的二叉树为例,目标和为 22:
plaintext
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
执行步骤分解:
初始调用 hasPathSum(5, 22)
根节点不为 null,调用 find(5, 22)
执行 find(5, 22)
5 不为 null
sum = 22 - 5 = 17
5 不是叶子节点(有左右子树)
左子树存在,调用 find(4, 17)
执行 find(4, 17)
4 不为 null
sum = 17 - 4 = 13
4 不是叶子节点(有左子树)
左子树存在,调用 find(11, 13)
执行 find(11, 13)
11 不为 null
sum = 13 - 11 = 2
11 不是叶子节点(有左右子树)
左子树存在,调用 find(7, 2)
执行 find(7, 2)
7 不为 null
sum = 2 - 7 = -5
7 是叶子节点(左右子树都为 null)
sum != 0,返回false
回到 find(11, 13) 的左子树处理
左子树搜索返回false,继续处理右子树
右子树存在,调用 find(2, 2)
执行 find(2, 2)
2 不为 null
sum = 2 - 2 = 0
2 是叶子节点
sum == 0,返回true
回到 find(11, 13) 的右子树处理
右子树搜索返回true,立即返回true
回到 find(4, 17) 的左子树处理
左子树搜索返回true,立即返回true
回到 find(5, 22) 的左子树处理
左子树搜索返回true,立即返回true
回到 hasPathSum 方法,返回true
整个过程清晰地展示了递归如何沿着路径5->4->11->2进行深度优先搜索,并在找到符合条件的路径后立即返回结果,避免了不必要的搜索。
算法复杂度分析
时间复杂度
在最坏情况下,算法需要遍历二叉树的所有节点(例如,当不存在符合条件的路径时)
对于包含 n 个节点的二叉树,时间复杂度为 O (n)
在最好情况下(例如,根节点到左叶子的路径就符合条件),时间复杂度为 O (1)(仅需访问几个节点)
空间复杂度
空间复杂度取决于递归调用栈的深度
在最坏情况下(斜树),递归深度为 n,空间复杂度为 O (n)
在最好情况下(平衡二叉树),递归深度为 log (n),空间复杂度为 O (log n)
此外,算法没有使用额外的辅助数据结构,空间效率较高
与迭代法(DFS)的对比
除了递归实现,我们还可以使用迭代法(基于栈)实现深度优先搜索:
java
运行
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) return false;
// 使用栈存储节点和当前路径的剩余和
Stack<Pair<TreeNode, Integer>> stack = new Stack<>();
stack.push(new Pair<>(root, targetSum - root.val));
while (!stack.isEmpty()) {
Pair<TreeNode, Integer> pair = stack.pop();
TreeNode node = pair.getKey();
int sum = pair.getValue();
// 检查是否为叶子节点且剩余和为0
if (node.left == null && node.right == null && sum == 0) {
return true;
}
// 右子节点入栈
if (node.right != null) {
stack.push(new Pair<>(node.right, sum - node.right.val));
}
// 左子节点入栈
if (node.left != null) {
stack.push(new Pair<>(node.left, sum - node.left.val));
}
}
return false;
}
两种实现方式的对比:
特性 递归实现 迭代实现
代码复杂度 低,逻辑清晰 较高,需要手动管理栈
空间复杂度 O (h),h 为树高 O (h),h 为树高
适用场景 树高较小时 树高较大时(避免栈溢出)
可读性 高,符合递归思维 较低,需要理解栈操作
性能 有函数调用开销 无函数调用开销,稍优
在实际开发中,递归实现更简洁直观,适合大多数情况;迭代实现则在处理极深的树时更可靠,不会出现栈溢出异常。
代码优化建议
这段代码的逻辑已经非常清晰,但可以从以下几个方面进行优化,提高可读性和效率:
1. 合并方法,减少代码量
可以将辅助方法find的逻辑合并到主方法中,减少方法调用开销:
java
运行
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) return false;
targetSum -= root.val;
// 叶子节点判断
if (root.left == null && root.right == null) {
return targetSum == 0;
}
// 递归搜索左右子树
return hasPathSum(root.left, targetSum) || hasPathSum(root.right, targetSum);
}
这个版本更为简洁,利用了逻辑或(||)的短路特性:如果左子树搜索返回true,则不会执行右子树搜索。
2. 避免不必要的 null 检查
原代码中对左右子节点的null检查可以省略,因为递归方法内部已经处理了root == null的情况:
java
运行
public boolean find(TreeNode root, int sum) {
if (root == null) return false;
sum -= root.val;
if (root.left == null && root.right == null) {
return sum == 0;
}
// 无需检查子节点是否为null,递归内部会处理
return find(root.left, sum) || find(root.right, sum);
}
这种方式减少了代码量,且逻辑更为紧凑。
3. 变量名优化
将sum改为remainingSum(剩余和)可以使代码意图更清晰:
java
运行
public boolean find(TreeNode root, int remainingSum) {
if (root == null) return false;
remainingSum -= root.val;
if (root.left == null && root.right == null) {
return remainingSum == 0;
}
return find(root.left, remainingSum) || find(root.right, remainingSum);
}
良好的变量名可以提高代码的可维护性,使其他开发者更容易理解代码逻辑。
常见错误与边界情况
在实现路径总和判断算法时,有一些常见的错误和边界情况需要注意:
1. 空树情况
当输入的根节点为null时,算法应返回false,原代码正确处理了这种情况。
2. 只有根节点的树
如果树中只有根节点,需要判断根节点的值是否等于目标和,且根节点是叶子节点:
plaintext
5
当目标和为 5 时,应返回true;否则返回false。
3. 目标和为负数的情况
算法应能正确处理目标和为负数的情况,例如:
plaintext
-2
\
-3
目标和为 - 5 时,路径-2->-3的和为 - 5,应返回true。
4. 节点值有负数的情况
当树中存在负数节点时,算法也应能正确判断,例如:
plaintext
1
/ \
-2 3
目标和为 - 1 时,路径1->-2的和为 - 1,应返回true。
常见错误实现
初学者常犯的错误包括:
没有检查节点是否为叶子节点,只要路径和等于目标和就返回true
累加路径和时出现计算错误
递归终止条件处理不当,导致空指针异常
没有利用短路特性,继续搜索已找到符合条件的路径
总结与思考
本文详细解析了基于递归深度优先搜索的二叉树路径总和判断算法,从代码结构到执行流程,再到复杂度分析和优化建议,全面展示了这一问题的解决方案。
这个算法的核心思想是:
利用递归进行深度优先搜索,遍历从根节点到叶子节点的所有可能路径
通过减去当前节点值的方式,追踪剩余需要满足的和
在叶子节点处检查剩余和是否为 0,以判断路径是否符合条件
利用短路特性,一旦找到符合条件的路径就立即返回
通过这个问题,我们可以学到:
递归在树结构遍历中的灵活应用
深度优先搜索的典型实现方式
路径问题的一般解决思路(追踪路径累积值)
边界条件处理的重要性
对于初学者来说,建议多动手模拟递归的执行过程,理解递归调用栈的变化和变量值的传递。同时,尝试用不同的方法(递归和迭代)解决同一问题,可以加深对算法思想的理解。
最后,这一问题的解决方案体现了 "减而治之" 的算法设计思想:将大问题(判断从根到叶子的路径和)分解为小问题(判断从当前节点到叶子的剩余和),通过解决小问题来最终解决大问题。这种思想在很多树和图的算法问题中都有广泛应用,掌握它对于提升算法设计能力非常有帮助。
迭代法
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*//*
*Stack Integer ArrayList String StringBuffer peek
*Collections imports LinkedList offer return
*empty polls offerLast pollFirst isEmpty
*List Deque append
*/
class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if(root==null) return false;Stack<TreeNode> jiedian=new Stack<>();Stack<Integer> zhi=new Stack<>();jiedian.push(root);zhi.push(root.val);while(!jiedian.isEmpty()){int size=jiedian.size();for(int i=0;i<size;i++){TreeNode node=jiedian.pop();int val=zhi.pop();if(node.left==null&&node.right==null&&val==targetSum){return true;}if(node.right!=null){jiedian.push(node.right);zhi.push(node.right.val+val);}if(node.left!=null){jiedian.push(node.left);zhi.push(node.left.val+val);}}}return false;}
}总结:
本文介绍了LeetCode 112题“路径总和”的两种解法:递归法和迭代法。递归法通过深度优先搜索(DFS)遍历二叉树,在叶子节点检查剩余和是否为零;迭代法则使用栈模拟递归过程。两种方法的时间复杂度均为O(n),空间复杂度取决于树的高度。文章详细解析了代码逻辑、执行流程和复杂度分析,并提供了优化建议和常见错误示例,帮助读者深入理解这一经典二叉树问题。
