动态规划算法的欢乐密码(五)：子数组系列(上)

专栏：算法的魔法世界

个人主页：手握风云

目录

一、例题讲解

1.1. 最大子数组和

1.2. 环形子数组的最大和

1.3. 乘积最大子数组

1.4. 乘积为正数的最长子数组长度

---

一、例题讲解

1.1. 最大子数组和

        在给定的数组中，我们需要找到一个连续的子数组，这个子数组中所有元素的和应该是所有可能的连续子数组中最大的。

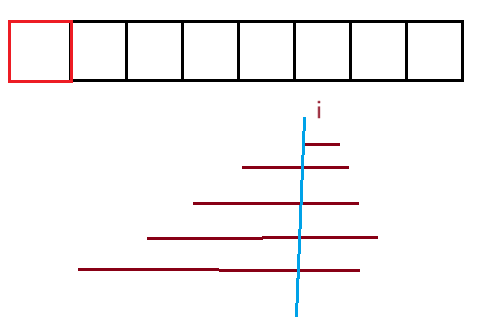
        我们以i位置为结尾，向前截取子数组，找出最大和，那么状态表示即为以i位置结尾，所有子数组的最大和。dp[i]可以分为两种情况：当子数组长度为1，最大和为nums[i]；当子数组长度大于1，nums[i]也得算上，和前面子数组的最大和，而前面的子数组又是以i-1位置为结尾，所以dp[i] = max(dp[i - 1] + nums[i - 1], nums[i - 1])。初始化的时候我们可以在前面加上虚拟头节点保证不越界，同时为了保证填表正确，可将dp[0]初始化为0。填表顺序从左到右。返回值，dp表中的最大值。

class Solution {public int maxSubArray(int[] nums) {int n = nums.length, ret = Integer.MIN_VALUE;int[] dp = new int[n + 1];for (int i = 1; i <= n; i++) {dp[i] = Math.max(dp[i - 1] + nums[i - 1], nums[i - 1]);ret = Math.max(dp[i], ret);}return ret;}
}

1.2. 环形子数组的最大和

        题目要求给定长度为`n`的“环形整数数组”nums，需找出“其中非空、且不重复使用原数组元素”的子数组的最大可能和，最终返回该最大值。核心特点：数组“环形”指末端与开头相连（子数组可同时包含原数组末尾和开头元素，如`nums=[5,-3,5]`的子数组`[5,5]`），但子数组不能重复取用原数组同一位置的元素；需覆盖两种子数组情况——不跨数组边界（如`[3]`）、跨数组边界（如`[5,5]`），取所有合法子数组的最大和。

        这道题可以分为两种情况，第一种情况：最终结果不在环上，相当于就是在求子数组的最大和。第二种情况：最终结果在环上，要想使子数组和最大，可以让环外部分的子数组和最小。

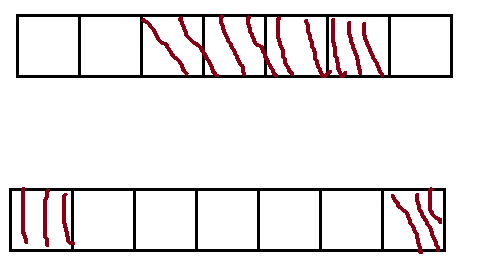
        那么本题的状态表示可以分为两种情况：f[i]表示以i位置为结尾所有子数组的最大和，g[i]表示以i位置为结尾所有子数组的最小和。参照上一题状态转移方程的推导，f[i] = max(f[i - 1] + nums[i], nums[i])，g[i] = min(g[i - 1] + nums[i], nums[i])。填表的时候可以在dp表前面引入虚拟头节点，当i = 1时，子数组最大和是它本身，那么f[0]和g[0]都可以初始化为0。填表顺序，从左到右。返回值，f需要返回里面的最大值。如果g里面全是负数，那么子数组最小和为本身，sum-sum(nums)=0，那么我们只需返回g里面的最小值；有正有负，sum-min(g)。

        完整代码实现：

class Solution {public int maxSubarraySumCircular(int[] nums) {int n = nums.length, sum = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i];}int fMax = Integer.MIN_VALUE, gMin = Integer.MAX_VALUE;int[] f = new int[n + 1];int[] g = new int[n + 1];for (int i = 1; i < (n + 1); i++) {f[i] = Math.max(f[i - 1] + nums[i - 1], nums[i - 1]);fMax = Math.max(f[i], fMax);g[i] = Math.min(g[i - 1] + nums[i - 1], nums[i - 1]);gMin = Math.min(g[i], gMin);}return sum == gMin ? fMax : Math.max(fMax, sum - gMin);}
}

1.3. 乘积最大子数组

        给定整数数组 nums，需找出数组中非空且连续的子数组，使得该子数组的乘积在所有可能的连续子数组中最大，最终返回这个最大乘积（题目保证结果为 32 位整数）。

        根据题目要求，本题的状态转移表示为：以i位置为结尾，所有子数组的最大乘积。如果子数组长度为1，dp[i] = nums[i]；如果子数组长度大于1，dp[i] = nums[i] * dp[i - 1]。这里需要判断dp[i - 1]与nums[i]正负情况。所以我们可以直接使用两个dp表f、g。f[i]表示以i位置为结尾，所有子数组的最大乘积；g[i]表示以i位置为结尾，所有子数组的最小乘积。如果nums[i] > 0，f[i] = max(nums[i], f[i - 1] * nums[i])；如果nums[i] < 0，f[i] = max(nums[i], g[i - 1] * nums[i])。我们不需要利用if-else判断，只需3个值取最大值。同理，g表的状态转移方程，min(nums[i], g[i - 1] * nums[i], f[i - 1] * nums[i] )。初始化的时候，因为是乘积，我们可以将2个dp表的第一个值初始化为1，同时保证下标的映射关系。填表顺序，从左到右两个表依次填写。返回值：返回f表里的最大值。

        完整代码实现：

class Solution {public int maxProduct(int[] nums) {int n = nums.length, ret = Integer.MIN_VALUE;int[] f = new int[n + 1];int[] g = new int[n + 1];f[0] = g[0] = 1;for (int i = 1; i <= n; i++) {f[i] = Math.max(nums[i - 1], Math.max(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]));ret = Math.max(ret, f[i]);g[i] = Math.min(nums[i - 1], Math.min(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]));}return ret;}
}

1.4. 乘积为正数的最长子数组长度

        给定整数数组nums，需找出其中乘积为正数的最长连续子数组，最终返回该子数组的长度。

        根据题目要求，本题的状态表示dp[i]为：以i位置为结尾，所有子数组乘积为正数的最大长度。当子数组长度为1时，如果nums[i]>0，dp[i]=1，如果nums[i]<0，dp[i]=0；当子数组长度大于1时，如果nums[i]>0，dp[i]=f[i]+1，如果nums[i]<0，要想乘积为正，那么就要使前面子数组的乘积<0，我们就会发现一个状态转移方程。

        f[i]以i位置为结尾，所有子数组乘积为正数的最大长度；g[i]以i位置为结尾，所有子数组乘积为负数的最大长度。如果g[i-1]==0，同时nums[i]<0，那么此时的f[i]应该=0，因为无法凑出乘积为正数。g[i-1]<0时，f[i]=g[i-1]+1。当nums[i]>0时，f[i]=f[i-1]+1；当nums[i]<0时，f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1。同样g表的状态转移方程也一样，当nums[i]>0时，g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1；当nums[i]<0时，g[i] = f[i - 1] + 1。填表顺序，两个表从左到右同时填写。返回值：f表里面的最大值。

        完整代码实现：

class Solution {public int getMaxLen(int[] nums) {int n = nums.length, ret = -1;int[] f = new int[n + 1];int[] g = new int[n + 1];f[0] = g[0] = 0;for (int i = 1; i <= n; i++) {if (nums[i - 1] > 0) {f[i] = f[i - 1] + 1;g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;} else if (nums[i - 1] < 0) {f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;}ret = Math.max(ret, f[i]);}return ret;}
}