运筹学——运输问题之表上作业法，西北角法，最小元素法

运输问题

常见的一个运输问题就是物流，这个是很贴合实际生活的。

数学模型

比如，共有m个产地A，n个销售地点B，每个产地的总产量为a_i，i = 1,2,3 ······m，且每个销售地点需要的货物数量b_j,j=1,2,3·····n，从A地到B地运输单位物资的单价c_ij,如表所示：

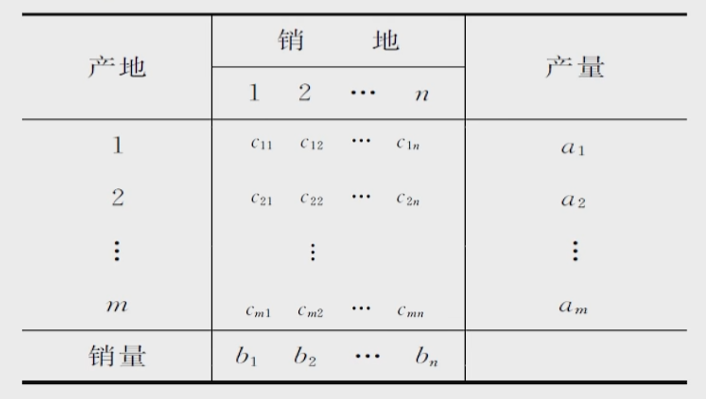
用x_ij表示从A_i到B_i的运输量，在产销平衡的条件下，要求总的运费最小的分配方案。运输货物的运费单价✖️运输量就是一共需要的运费开支，令这个开支最小就是这个运输问题的最优解，也就是min z = ∑c_ij ∑ x_ij，这个是两层的加和运算。
第一个约束条件就是每个产地的运输量都要达到，不能超出，也不能剩余，对应数学表达就是：∑x_ij=a_i，i=1,2,····n.（这个是行约束）
第二个约束条件就是每个销地所需要的货物需要全部送到位，对应的数学表达就是：∑x_ij=b_j，j=1,2,····m。（这个是列约束）
因此，综合下来就是如下所示的数学模型：

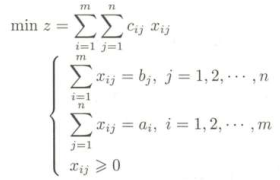
从这个数学模型上就很清晰的看到一共有mn个变量，有（m+n）个约束方程。

关于建立运输问题的数学模型，举个🌰会更好理解

假设一公司从两个产地A₁,A₂,把物品运输到三个销地B₁,B₂,B₃,各地的产量和销量，以及每件物品所需的运费如下表所示，那么如何调度才能使运费最少呢？

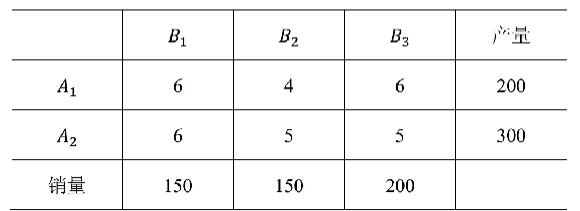
我们先列出这个问题的数学模型，过程如下：

假设，从A_i到B_i的运输量为x_ij,那么就可以列表为：

就有：

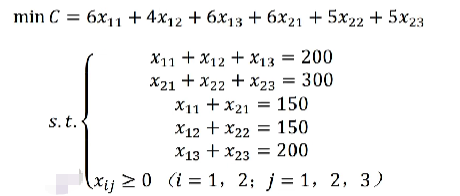
这个运输问题也可以用表格来表示就是：

其中，c_ij表示的是单位运价，x_ij表示的是这条路线上需要运输的货物量，当x_ij的值时0时，就表示不需要在这条路线上运输货物。

对于上面那个例题而言，它的系数矩阵为：

那么推广到一般情况的系数矩阵结构如下图所示：

这个系数矩阵的特点是：

1. 先看前m行，在第一行中，每个1所在位置对应的都是第一行中的元素，也就是x_1i第二行中，每个1的位置对应的都是第二行的元素，也就是x_2i，依次类推，前m行都对应的是行约束，
2. 再看后n行，第m+1行中，每一个1所在的位置都对应的是第1列，也就是x_i1，第m+2行中，每一个1所在的位置都对应的是第2列，也就是x_i2，依次类推，后n行所对应的都是列约束。

如果看文字有点不明白的话，那就拿刚才的例子来说：

因此，对于这类表，有以下的特点：
1，以列的方向上看，比如第一列向量P₁₁，对应的第一行和第m+1行的位置上元素都是1，其它的都是0，再比如列向量P₂₂，对应的第二行和第m+2行的元素为1，其它的都是0。如果把列单独拿出来看其实就是P_ij的列向量中，第i个元素和第m+j个元素都是1，其余的都是0.因此就得到一个式子：

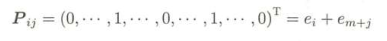
e_i = (0···，1，···0）^T表示的意思是第 i 个元素是1，其他的都是0。
2，因为是产销平销的运输问题，所以有产出就等于销量，这里令总量为Q，也就是有：

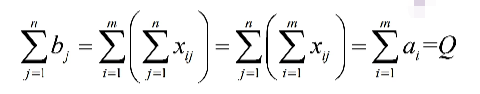
表达的意思就是不管是按列求和还是按行求和，总数都是一定的。

3，产销平衡的运输问题，一定存在可行解：

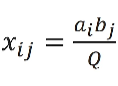
对于这个公式的应用，还是以上面的例子来解释：

x的解法如上图，想必现在已经懂了它的用法。

由于这个表有很多便于计算的特征，所以在求运输问题的时候，就习惯上称这种方法是表上作业法。

表上作业法

本质还是单纯形法

步骤

1，在产销平衡表上用西北角法，或者最小元素法，来找初始的基可行解，用Vogel法给出m+n-1,它们就是初始基变量的取值。
2，求非基变量的检验数，在表上计算空格的检验数，没有空的格检验数就是0，
3，确定出基变量与入基变量，找新的可行解，用闭回路法调整。
4，再重复2,3的步骤，一直到确定是否符合最优解的条件才停止。

西北角法

举个例子🌰：
还拿上面的例子来说明

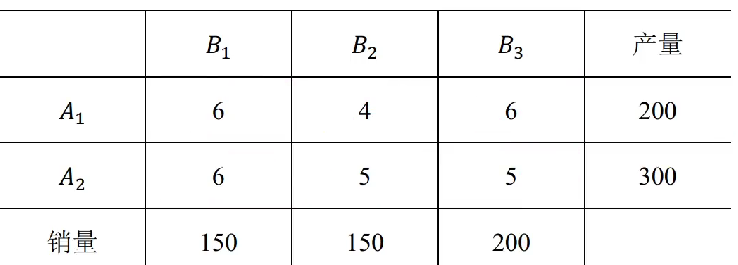
首先确定这个表中的产出是平衡的，行向和与纵向的和都是500。
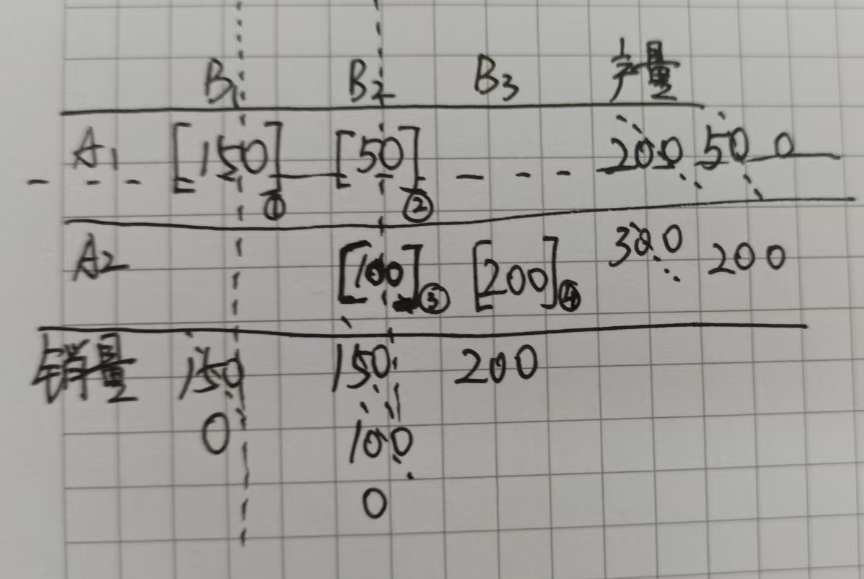
其次，就只看这个表的中间部分，有6个格子，那么西北角就对应的是A₁B₁。因为B一共需要150个，A₁的总产量是200，所以这个位置最大可以填150，此时A₁的产量就剩下200-150=50个，那么B₁的需求量就都得到了满足，所以销量在此时就是150-150=0，如下图：

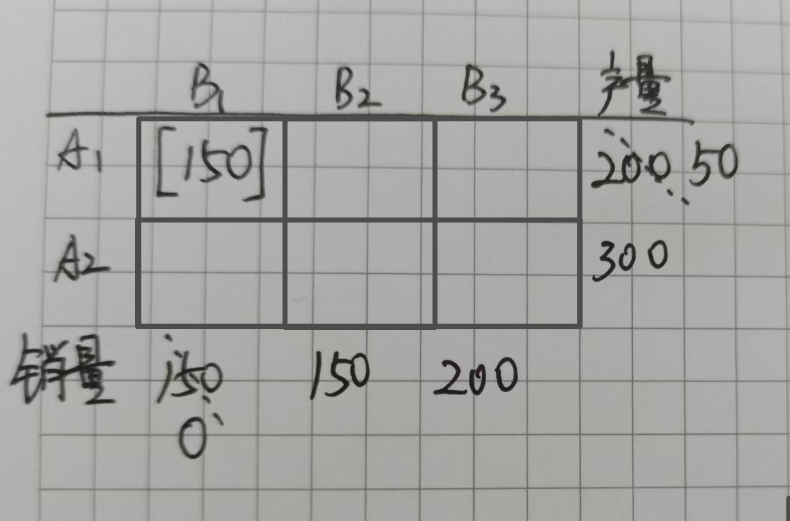
此时，由于B₁列的需求量都满足了，所以就可以划去第一列，如下图：

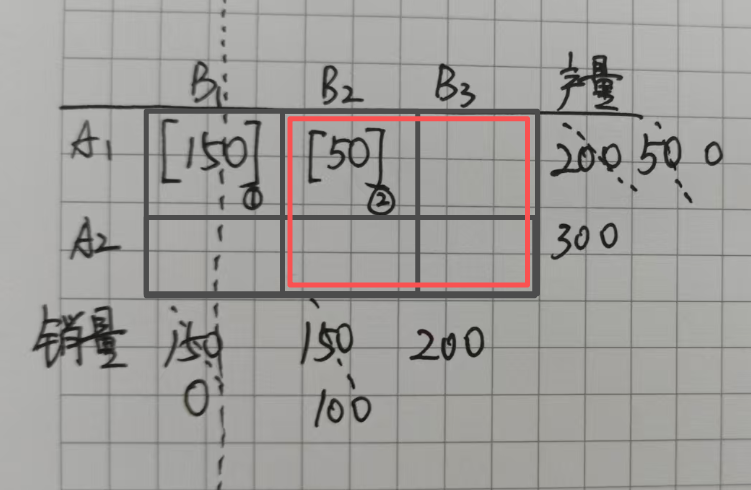
在剩下的表格中，西北角的位置就是A₁B₂，又B₂需要50个量，但是A₁的产出量只剩下50，所以这个位置只能填50，此时，B₂的需求量就是150-50=100，A₁的产出量就是50-50=0，这时，A₁的产出量都分配完了，所以可以划去第一行，如下所示：

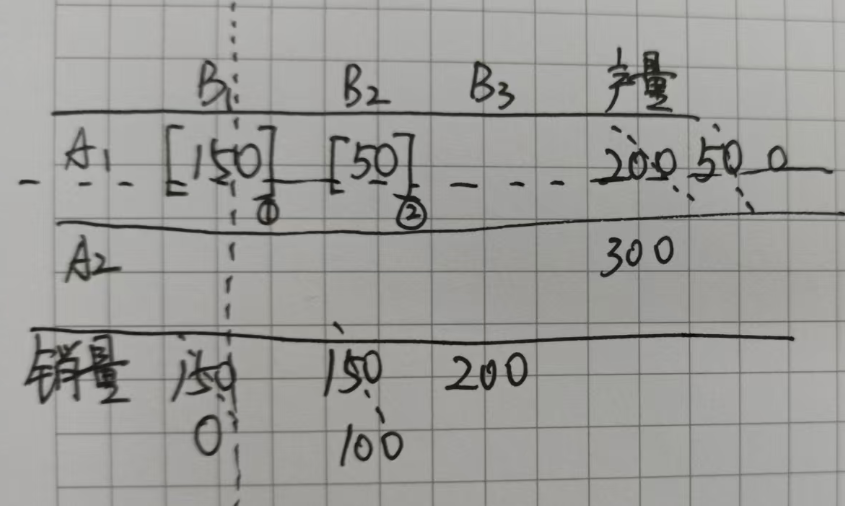
接着再看剩下空白格的西北角，也就是A₂B₂,B₂的需求量还剩100，A₂的产出有300，所以这个位置就要填100，此时，A₂的产出为300-100=200，B₂的需求已经全部满足，那么就可以划去B₂这一列，如下：

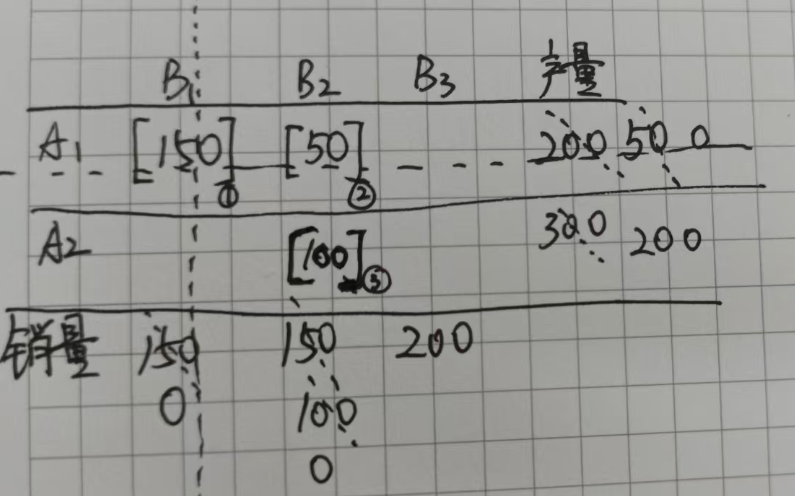
最后还剩一个空格就是A₂B₃的位置，这个时候A₂的产出还剩余200，B₃还需要200，正好填200，就保证了产销平衡，如下所示:

最小元素法

就近供应，优先选择单位价格低的优先供应

直接来举个例子说明这个方法：
假设表1是单位运价表，如下图：

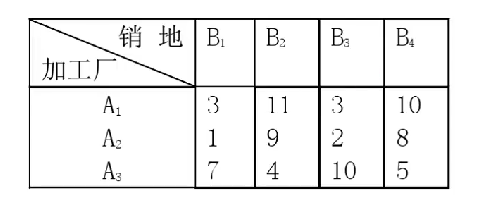
表2是产销平衡表，如下图：

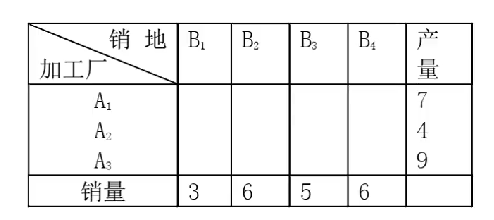
首先在表1的单位运价表中找最小的运价开始确定运销关系，表1中最小的是1，它对应的是A₂向B₁运输，在表2中发现A₂可以运输4个，但是B₁只需要3个，所以在3,4中填较小的数3，那么此时A₂的产量就是4-3=1个，B₁的销量就是3-3=0，所以就可以根据这个0划去表1中的第一列了，如下图：

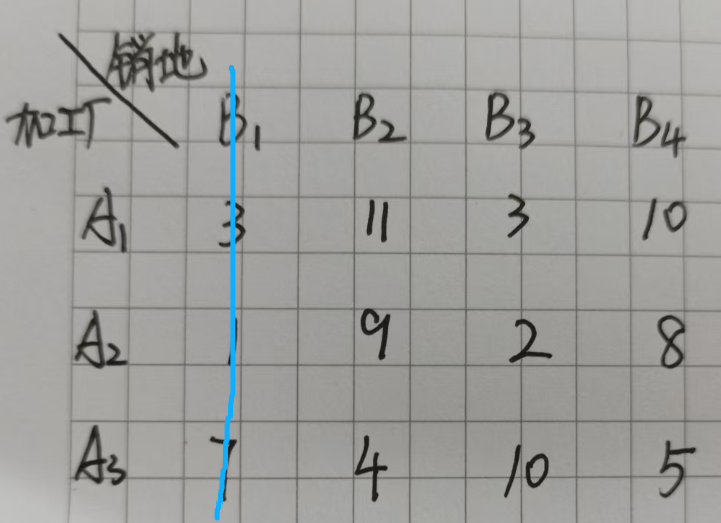
在表1中除了被划去的部分，在剩余的数值中找最小的数，发现是2。
又因为2代表的是A₂向B₃运输，所以在表2中发现B₃需求量是5，但是A₂的产量剩余1个，在4,1中选择小数填进去，那就是1，此时A₂产量此时就是1-1=0，B₃的需求量就是5-1=4，如下图：

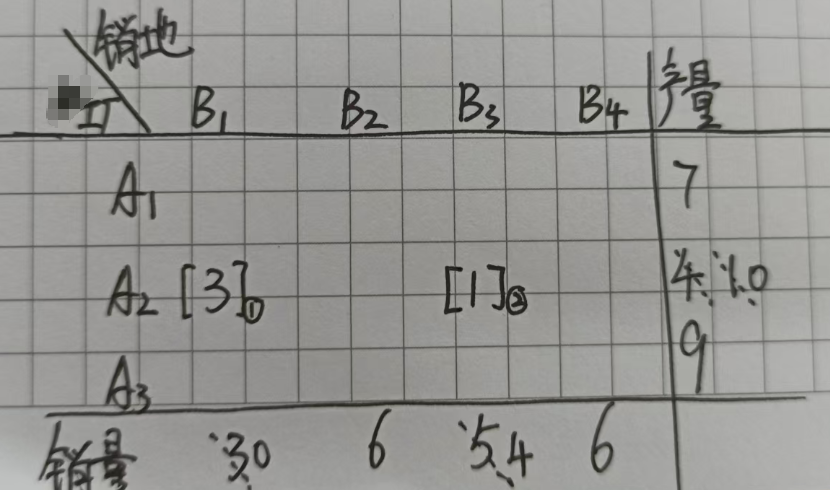
因为A₂对应的产量是0，所以在表1中就可以划去第二行，如下图：

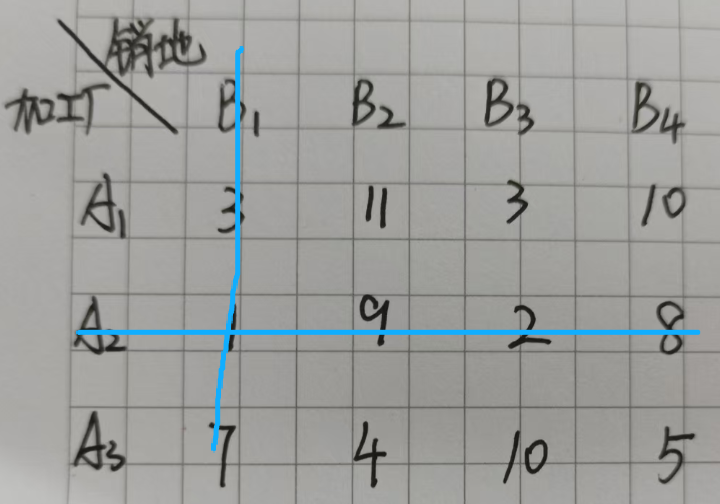
再在剩下的数值中找最小的数，发现是3。
依照上面的方法继续重复，一直到表1中所有的行列都划去完，就说明所有的货物运输方式都已经安排结束了，最后的结果如下图：

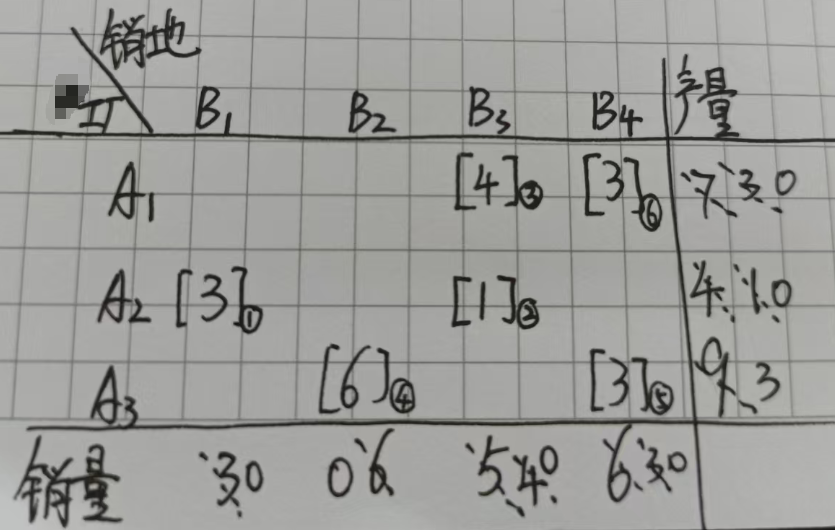
最后就得到如图所示的结果了，用变量表示就是：

其它的位置就是0
结合运价，结果就是：