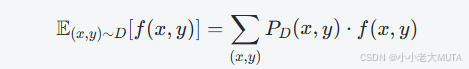DPO原理 | 公式推导
参考视频:DPO (Direct Preference Optimization) 算法讲解_哔哩哔哩_bilibili
预备知识掌握:
PPO原理详解 | 公式推导-CSDN博客
PPO的训练过程(伪代码)-CSDN博客
KL散度
KL散度,又称“相对熵”,是衡量两个概率分布之间差异的非对称性度量。
上面公式表示:P分布相对于Q分布的相似程度。KL散度大于等于0。
P和Q越相似,KL散度越接近0;如果P和Q分布完全一致,则KL散度等于0。
注意,KL(P || Q)等于 KL(Q || P).
Bradley-Terry模型
Bradley-Terry模型,是一种用于建模成对比较结果的概率模型,用于衡量不同“元素”或“选手”的相对实力,进而预测它们之间的胜负概率。
假设有若干个元素(选手、队伍等),对应的实力参数分别为 ,其中
>0 表示第 i 个元素的实力。
两个元素i 和 j 之间的胜负概率定义为:
- P(i>j) 表示元素 i 战胜元素 j 的概率。
举例如下:
| 对战 | 胜 | 负 |
|---|---|---|
| A 对 B | 8 | 4 |
| A 对 C | 3 | 5 |
假设观察到的比赛结果服从Bradley-Terry模型,目标是 通过最大化对数似然函数来估计示例参数。
对于 A和B 的12场比赛中,出现8胜4负结果的概率计算是下面这样的:
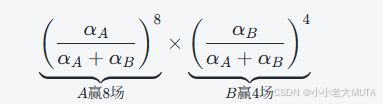
对于A和C之间的8场比赛,出现3胜5负的概率计算是这样的来的:
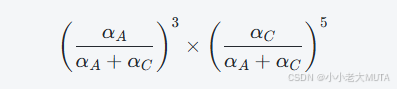
我们假设所有的比赛结果相互独立,那么整体观察到的比赛结果的概率就是所有比赛概率的乘积:
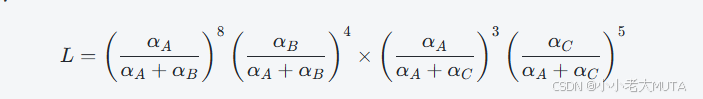
我们实际想要求解的参数是,通过最大化对数似然函数lnL,找出最优可能产生这个结果的观测参数
。
如何求得最大lnL?--->通过优化器。
将结果转换为损失,损失越小,lnL越大。
![]()
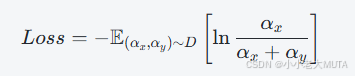
公式解释:
期望展开如下:
PD(x,y) 是“对战对 (x,y) 出现的概率”。对应了之前的8,4,3,5。
强化学习
在强化学习中,大模型输入是x,输出是y。通过Reward模型对输出y进行评估,评分可能是负值。
在RLHF中,数据中会有好的回答y1,分数为r(x,y1),以及不太好的回答y2,分数r(x,y2).
将r1和r2 用“回答 y1 更好于回答 y2”的概率P(y1>y2)将两个参数进行联系,我们希望通过训练使得y1尽可能优于y2,也就是希望P(y1>y2)尽可能趋近于1。
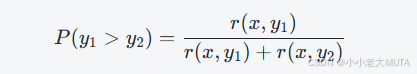
因为评分r可能出现负数,所以加上指数函数:
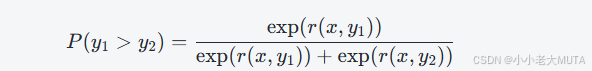
P(y1>y2) 表示根据Reward模型预测 y1 比 y2 更优的概率。
整体流程:
- 先用人工标注或模型训练得到Reward模型 r(x,y)。
- 给一组回答对,计算 P(y1>y2)。
- 用这个概率作为损失(负对数似然)训练Reward模型或引导策略更新。
如何通过训练将概率增大?将损失表示为概率的负数,通过优化器,损失越小,概率越大。
![]()
公式转换:
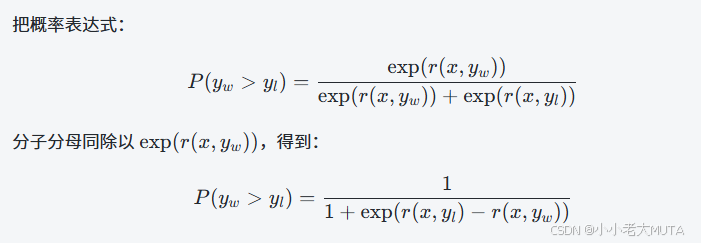
又因为sigmoid公式表示为:
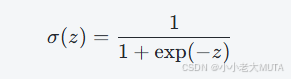
因此,概率表达式可以变换为:

损失就是:
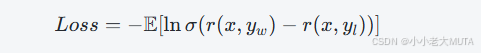
目标就是,使得越大越好。
RLHF-->DPO
在PPO中,引入KL散度的损失表达式如下:
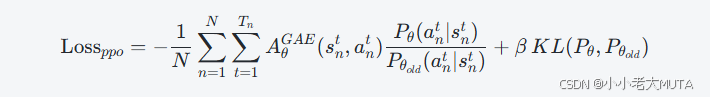
笼统的RLHF表达是:

对这个公式进行变换:
首先展开KL散度期望,最大化等价为最小化负值,利用对数指数等式
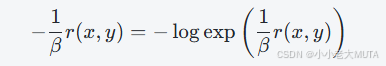
得到:
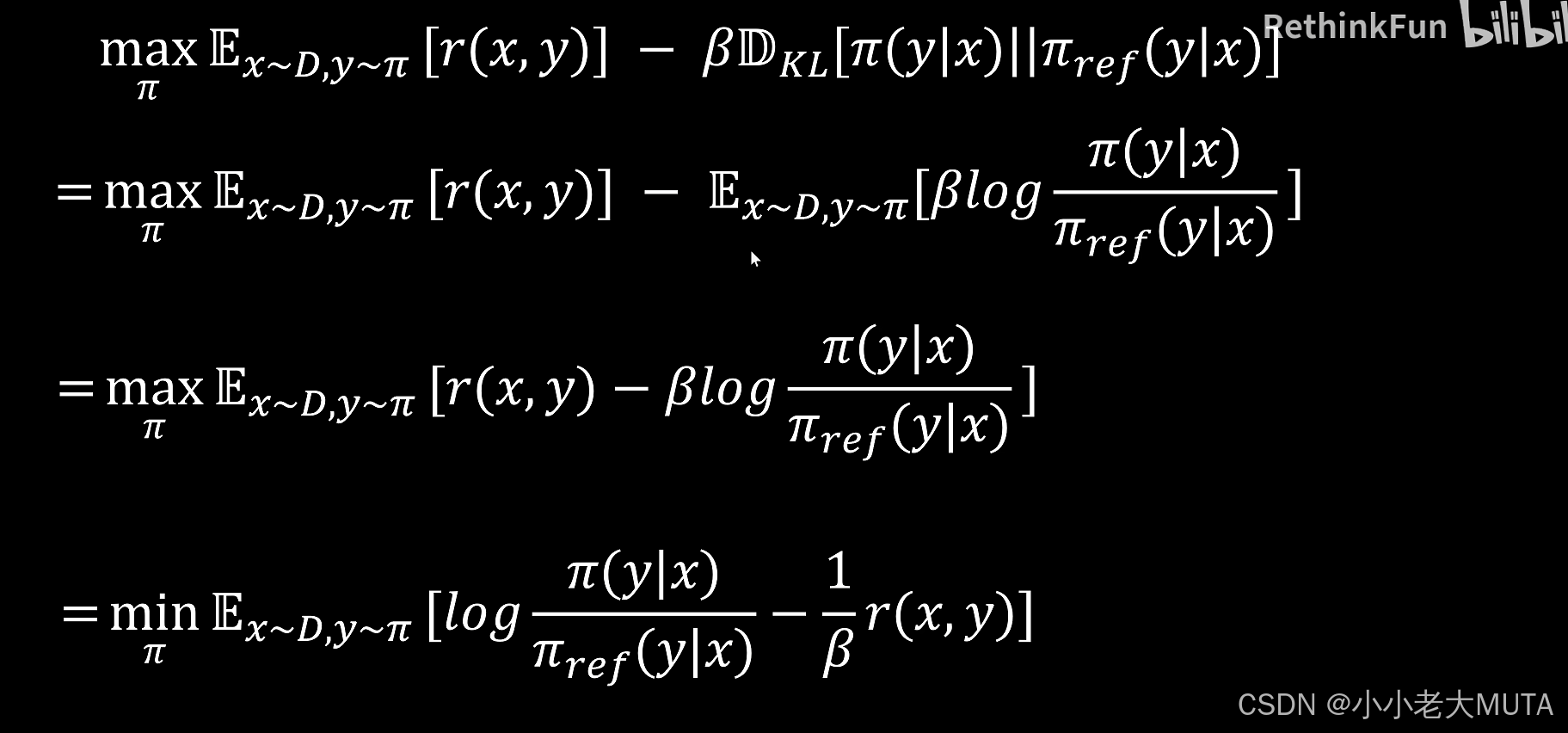
引入归一化常数Z(x),定义:
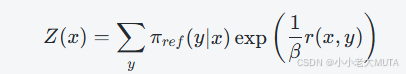
将分母调整为概率分布形式:
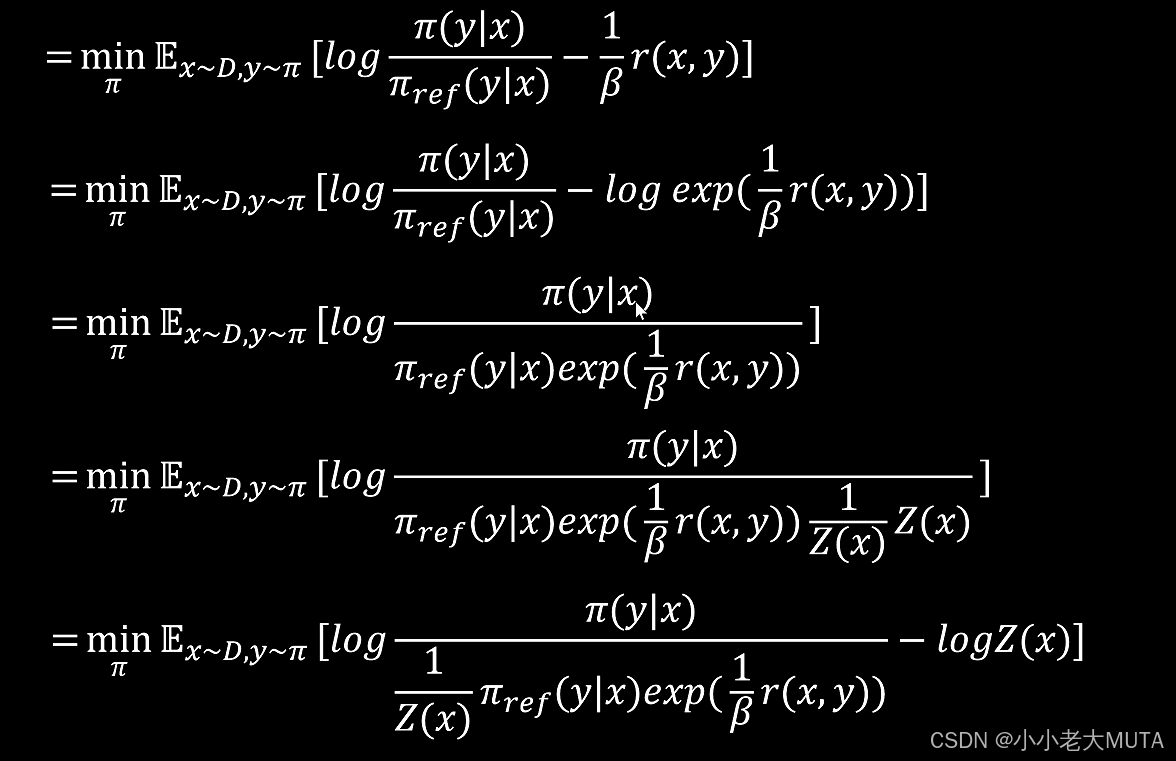
因为logZ(x)与优化无关(不依赖于Π),所以可以忽略这个常数项。
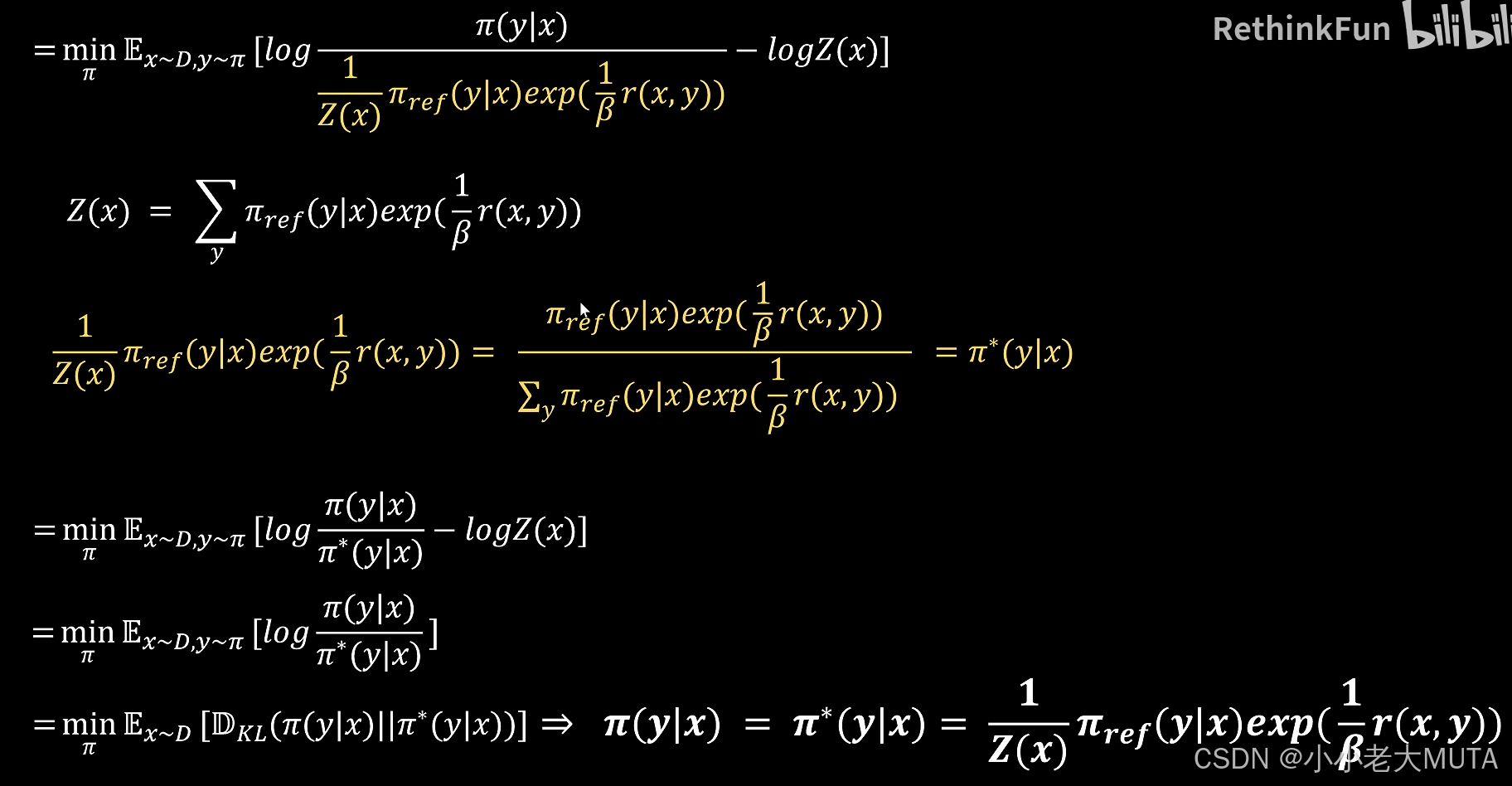
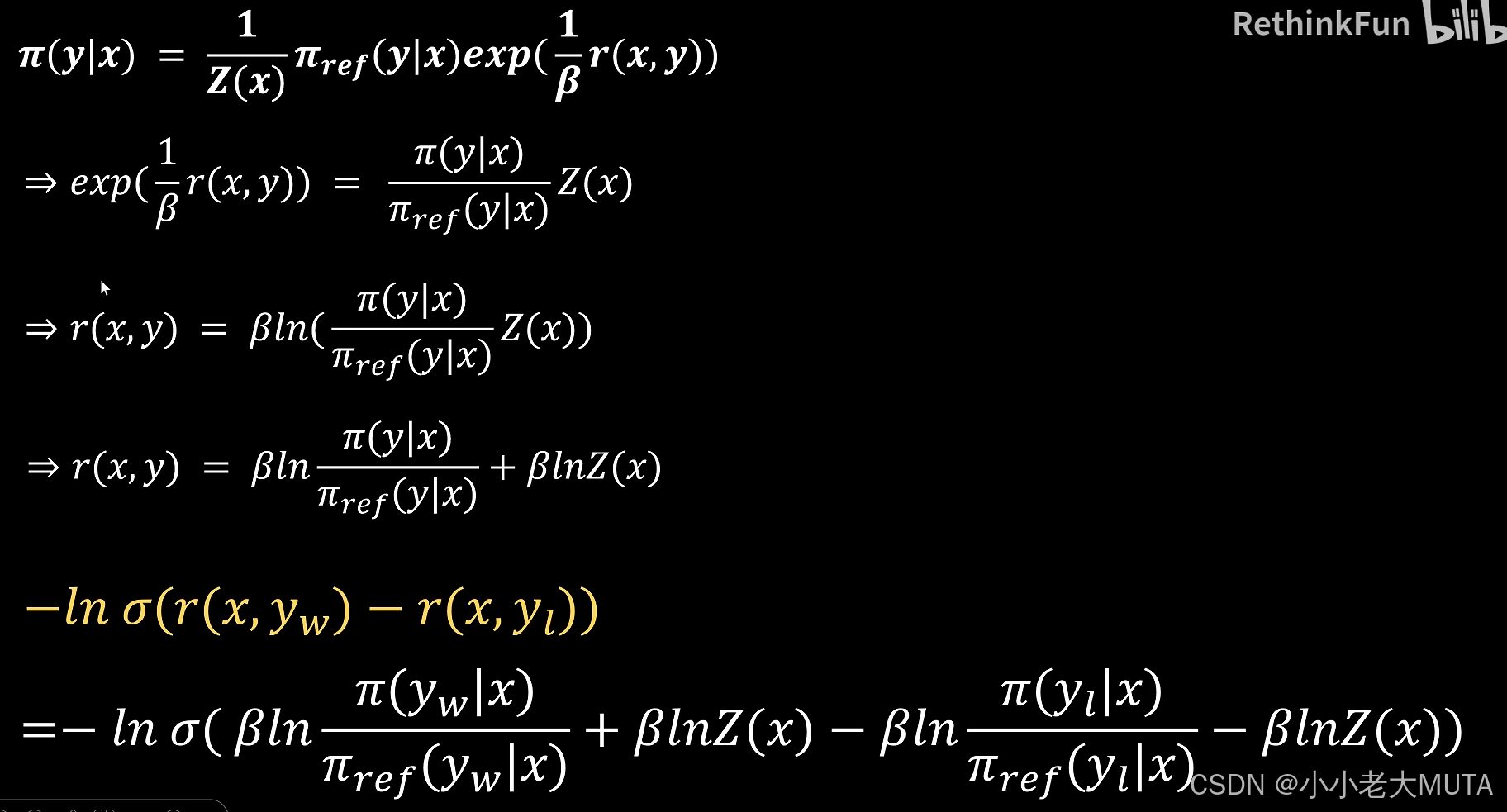
得到最终DPO Loss:
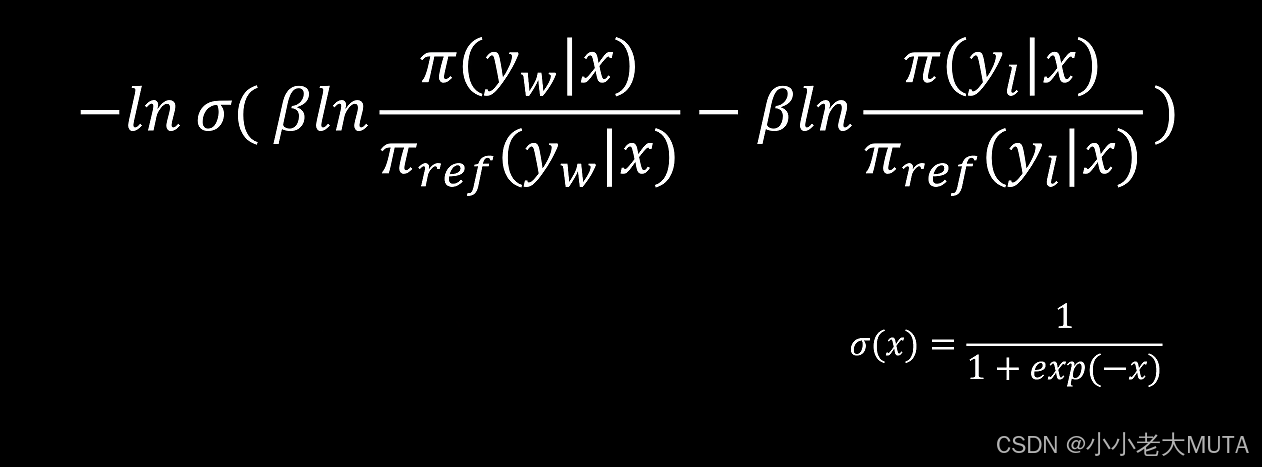
人麻了,,先截个图放这儿,,后期再详细注解。