当前位置：首页 > news >正文

2026年ESWA SCI1区TOP，适应性社会流动性重构差分进化算法ASMRDE，深度解析+性能实测

news 2025/9/10 9:40:43

1.摘要

差分进化算法（DE）被广泛认可为一种高效全局优化算法，大多数现有DE算法采用贪婪选择算子，这种简单而有效的策略主要关注个体级进化，忽视了种群级进化。因此，算法未能充分利用种群的整体信息，限制了其优化性能。为了解决这一问题，本文提出了自适应社会流动性重构差异进化算法（ASMRDE），该算法引入了一种社会代际选择机制，实现了种群级进化与个体级进化的同步进行，通过社会代际的迭代过程克服了传统方法局限性。此外，ASMRDE构建了一个外部档案，用于保存社会重构过程中被淘汰历史种群，这些历史信息在后续的社会重构和个体进化中得到了有效利用。ASMRDE还引入了一种基于狭义多样性的参数适应策略，并提出了一种新的变异策略，利用历史种群信息指导个体进化。

2.适应性社会流动性重构差分进化算法ASMRDE

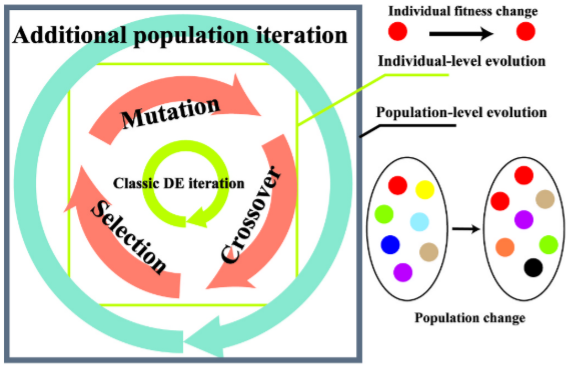
Schematic of social restructuring mechanism

ASMRDE算法引入了基于代际关系的社会代际选择机制、"DE/current-to-unique_pbest/1 with external archive”变异策略和基于狭义多样性指数的自适应控制参数机制，旨在解决全局优化问题。通过在个体级进化基础上引入种群级进化，ASMRDE保持种群结构健康，提升了算法的整体效率和性能，实现了探索与开发之间的平衡。

社会结构重构机制

社会结构重构机制模拟现实世界中的代际关系和社会结构，将迭代分为自然代（g）和社会代（G）。自然代代表时间的增长，社会代则对应历史区间内形成的群体，这些群体共享相似的历史经历和价值观，并通过代际冲突（IC）、代际公平（IE）和代际流动性（IM）等概念，反映了现实中的社会动态。

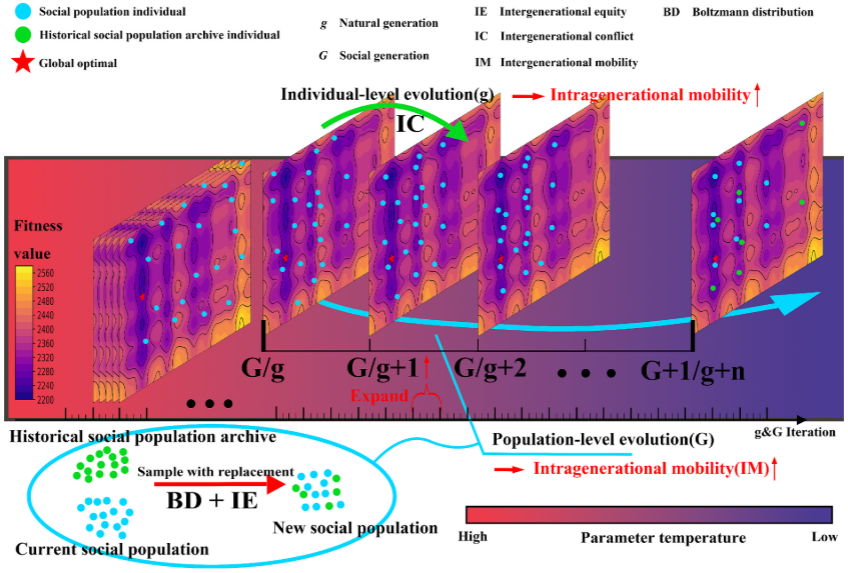
Social restructuring mechanism expands into a linear structure

ASMRDE引入了双层进化结构，包括个体级进化和种群级进化。在个体级进化中，采用贪婪选择过程来模拟个体的增长；在种群级进化中，通过社会重构机制实现种群更新。社会重构基于玻尔兹曼分布，从当前和历史种群中选择个体，并将未选中的个体加入历史档案，确保多样性和向上的代际流动性。

策略采用玻尔兹曼分布计算选择概率，根据个体适应度在社会重构过程中确定下一个社会个体。对适应度进行预处理规范化：
$Fi=fi−μσF_i=\frac{f_i-\mu}{\sigma}$

基于规范化适应度值，可以使用玻尔兹曼分布计算选择概率：
$probi=exp⁡(−Fi/T)∑m=1NPexp⁡(−Fm/T)prob_i=\frac{\exp(-F_i/T)}{\sum_{m=1}^{NP}\exp(-F_m/T)}$

参数适应策略

变异策略的贪婪度随着评估次数的增加而调整 $p$ 值：
$p=pmax−(pmax−pmin)×(nFEs/MFEs)p=p_{max}-(p_{max}-p_{min})\times(nFEs/MFEs)$

在算法中，狭义多样性定义为种群中非重复决策向量的比例，这有助于调节探索与开发之间的平衡。根据狭义多样性和评估次数，参数 $CR$ 也会相应调整，以提高局部开发的效率。
$div=NPuniqueNPdiv=\frac{NP_{unique}}{NP}$

$CR=max⁡(min⁡(N(MeanCR,0.1),1),0)CR=\max\left(\min\left(N(Mean_{CR},0.1),1\right),0\right)$

$MeanCR={0.92,ifdiv>0.74andnFEs/MFEs>0.50.90,otherwiseMean_{CR}= \begin{cases} 0.92, & \mathrm{if}div>0.74\mathrm{and}nFEs/MFEs>0.5 \\ 0.90, & \mathrm{otherwise} & \end{cases}$

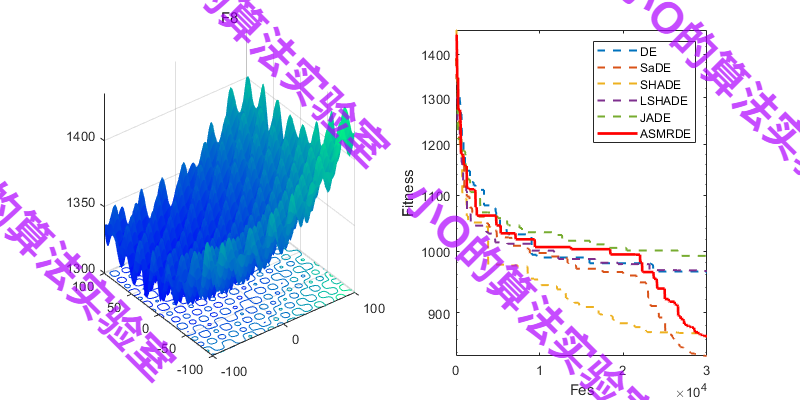
3.结果展示

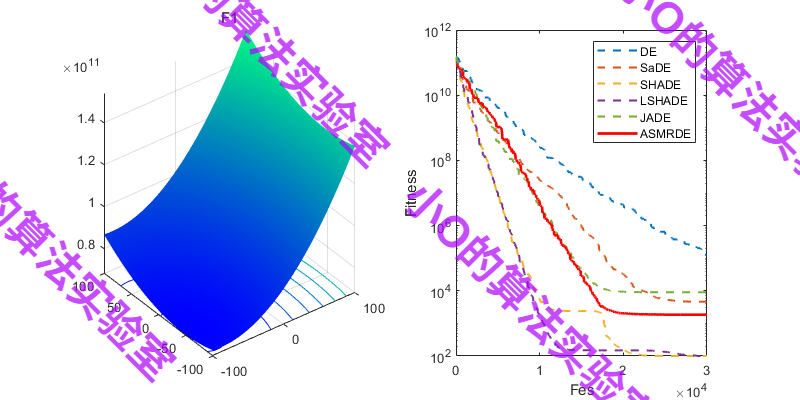
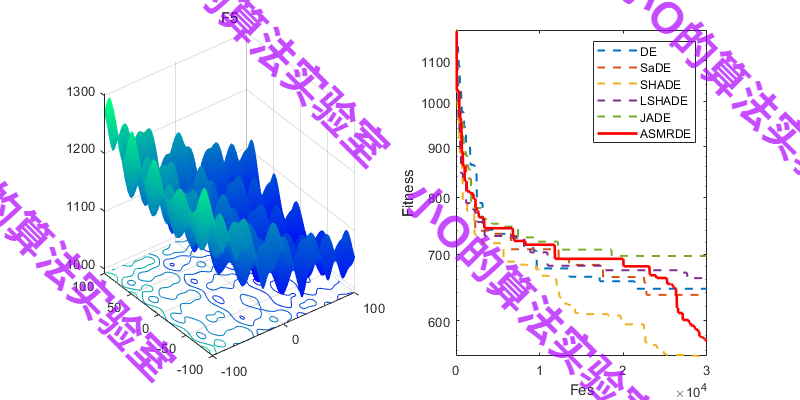
4.参考文献

[1] Zhuo Y, Yang Q. Adaptive social mobility-restructuring differential evolution for global optimization[J]. Expert Systems with Applications, 2026, 297: 129528.