当前位置：首页 > news >正文

SME-OLS

news 2025/9/10 9:30:08

OLS 三个式子

真实值与残差 (residual)

定义：

$ei=yi−y^ie_i = y_i - \hat{y}_i$
- $y_i$ ：第 i 个样本的真实观测值；
- $y^i\hat{y}_i$ ：回归模型给出的预测值；
- $e_i$ ：残差（residual），是“真实值 - 预测值”。

总体模型（理论模型）

形式：
$Yi=β1+β2Xi+εiY_i = \beta_1 + \beta_2 X_i + \varepsilon_i$
- $β1,β2\beta_1, \beta_2$ ：总体的真实参数（未知）；
- $εi\varepsilon_i$ ：随机误差项，捕捉未观测因素和随机性。

这是 理想中的经济学/统计学关系，但参数 $β\beta$ 和误差分布我们不知道。

样本估计模型（回归方程）

形式：

$Y^i=b1+b2Xi\hat{Y}_i = b_1 + b_2 X_i$
- $b_1, b_2$ ：由样本数据计算出来的 OLS 估计量（估计 $β1,β2\beta_1, \beta_2$ ）；
- $Y^i\hat{Y}_i$ ：预测值（fitted value）。

在样本数据上估计出来的拟合直线。

三者关系梳理

总体模型（理论层面）
$Yi=β1+β2Xi+εiY_i = \beta_1 + \beta_2 X_i + \varepsilon_i$

——描述数据的真实生成机制。
样本模型（估计层面）
$Y^i=b1+b2Xi\hat{Y}_i = b_1 + b_2 X_i$

——用 OLS 得到的估计直线，代替未知的真实直线。
残差（误差的样本体现）
$ei=yi−y^ie_i = y_i - \hat{y}_i$

——衡量预测值与观测值的差距。

b和 $β\beta$ 之间的联系

二者的关系

在统计学上, $b_1$ 和 $b_2$ 是 $β1,β2\beta_1, \beta_2$ 的 无偏估计量：

$E(b1)=β1,E(b2)=β2E(b_1) = \beta_1, \quad E(b_2) = \beta_2$
这意味着：如果我们无限次重复抽样并每次计算 $b_1$ ，它们的平均值会等于真实参数 $β1\beta_1$ 。

直观理解

β：真理（总体直线），但我们看不见；
b：猜测（样本直线），是用数据近似出来的；
b 不是 β，但在长期来看，bb的平均会逼近 β。

Least squares estimates

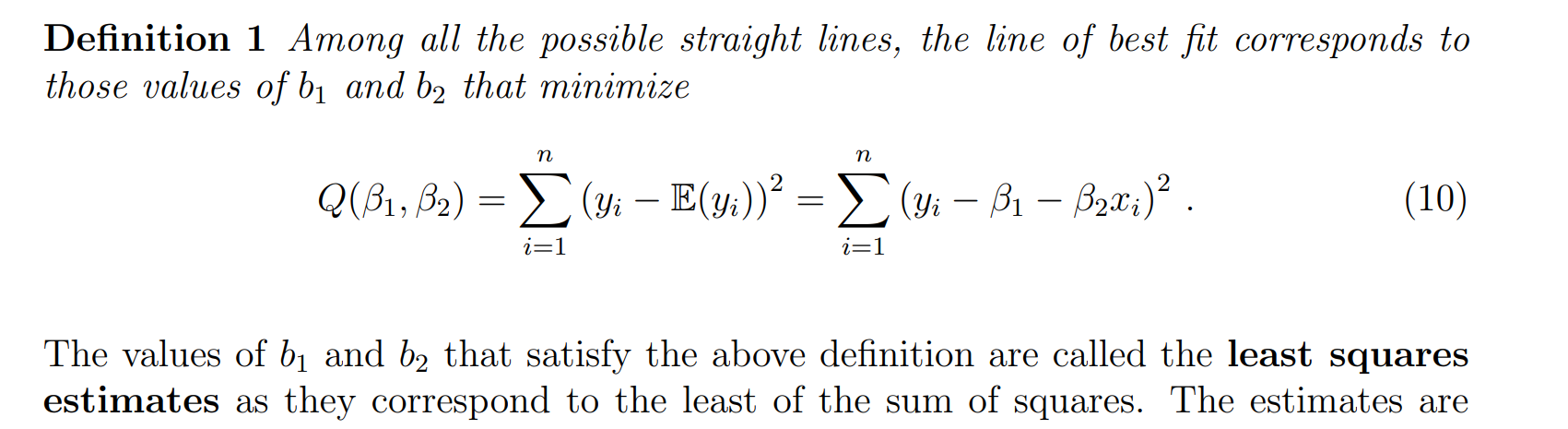
对β进行求偏导：
$∂Q∂β1=−2∑in=(yi−β1−β2xi)=0(1)\frac{ \partial Q }{ \partial \beta_{1} } = −2 \sum^n_{i}= (y_i − β_{1} − β_{2}x_{i}) = 0 \quad (1)$

$∂Q∂β2=−2∑in(yi−β1−β1xi)xi=0(2)\frac{ \partial Q }{ \partial \beta_{2} } = −2 \sum^n_{i} (y_{i} − β_1 − β_{1}x_{i}) x_{i} = 0 \quad (2)$

对 $（ 1 ）$ 进行化简：
$b1=yˉ−b2xˉ(3)b_{1}=\bar{y}-b_{2}\bar{x}\quad (3)$

对（2）进行化简：

$∑i=1nyixi−b1∑i=1nxi−b2∑i=1nxi2=0(4)\sum_{i=1}^ny_{i}x_{i}-b_{1}\sum_{i=1}^nx_{i}-b_{2}\sum_{i=1}^nx_{i}^2=0\quad(4)$

带入（3）到（4）

$b2=SxySxxb_{2}=\frac{S_{xy}}{S_{xx}}$

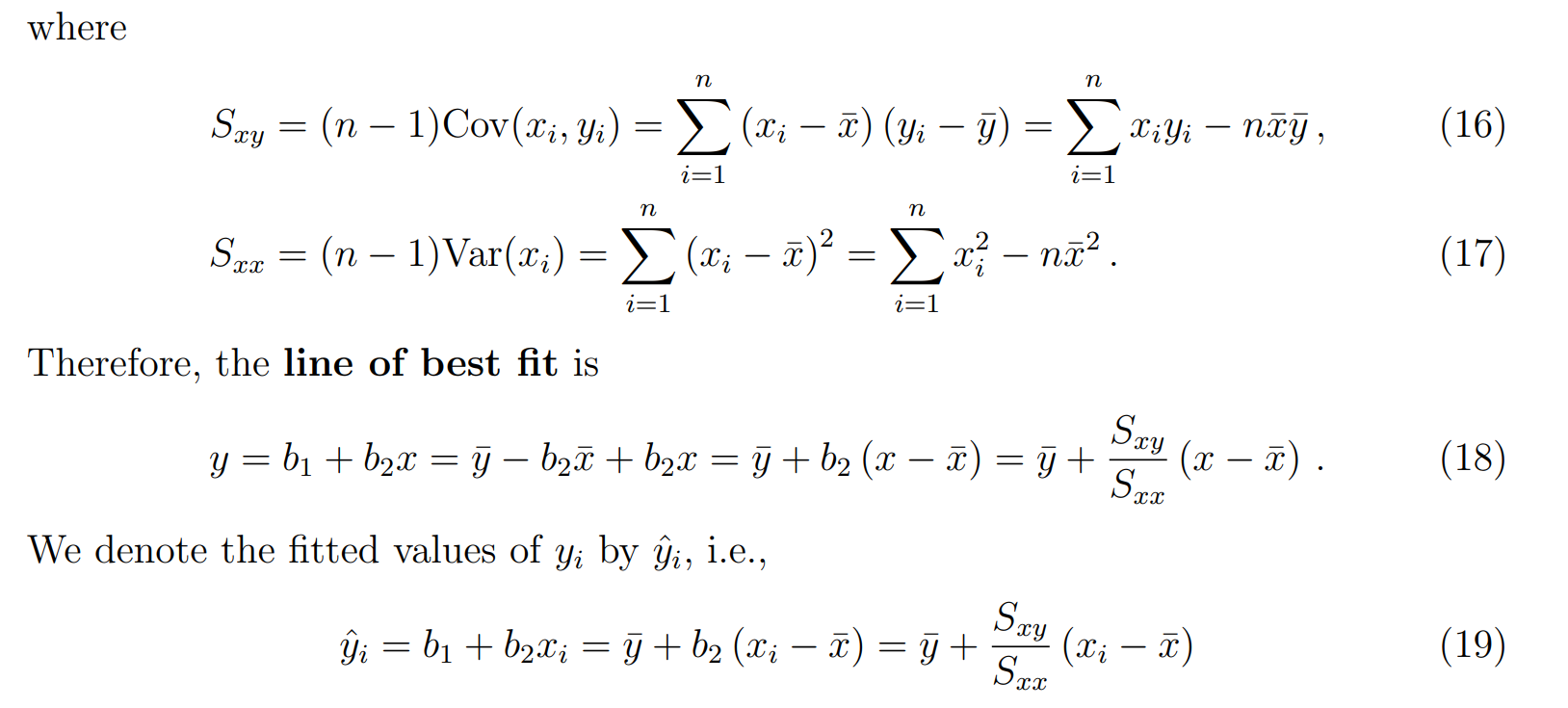
Properties of the fitted regression line

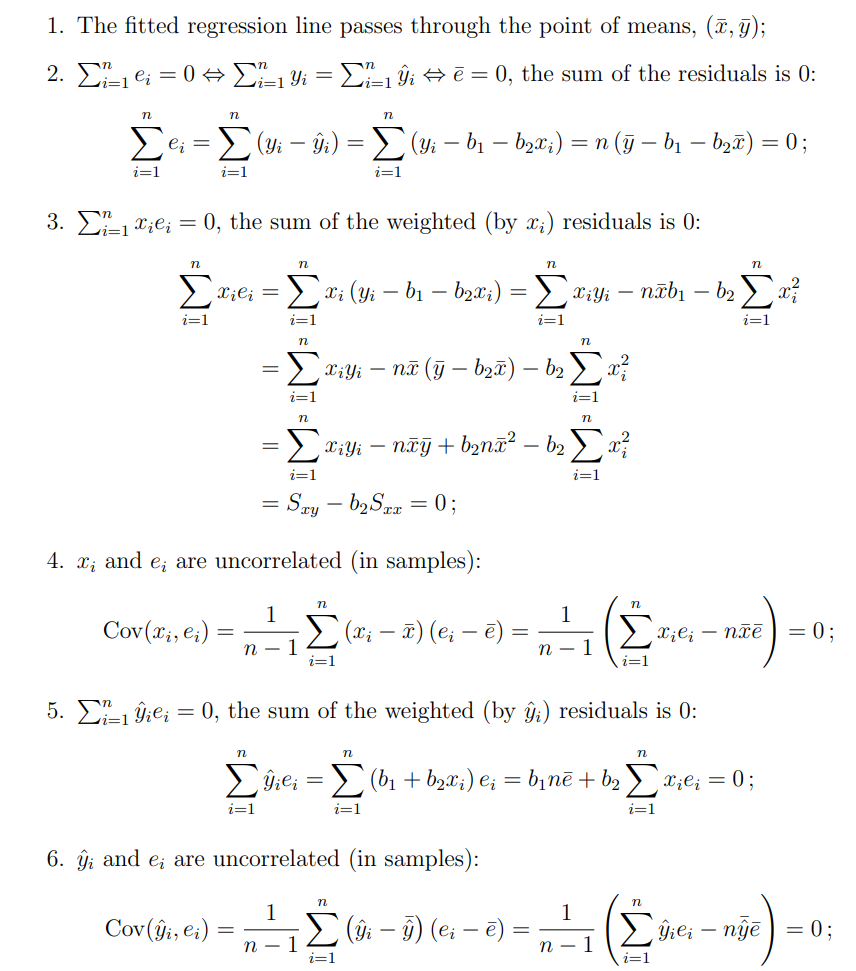
性质4：

性质6：

协方差的定义里一定要减去均值（否则只是内积，不是协方差）；

因为 $eˉ=0\bar{e} = 0$ ，所以：

$Cov(y^i,ei)=1n−1∑i=1n(y^i−y^ˉ)ei\mathrm{Cov}(\hat{y}_i, e_i) = \frac{1}{n-1} \sum_{i=1}^n (\hat{y}_i - \bar{\hat{y}}) e_i$

这就说明了：协方差公式里确实要减去 $y^\hat{y}$ 的均值，只是因为残差的均值为 0，才只剩下 $y^i−y^ˉ\hat{y}_i - \bar{\hat{y}}$ 。

Sample Correlation coefficient

回归分析中的作用

在 一元线性回归中：

$R^2 = r_{xy}^2$

也就是说，相关系数的平方等于判定系数 $R^2$ ，它衡量模型对因变量 y 变异的解释程度。
因此，相关系数不仅衡量关系强弱，还能告诉我们回归直线“拟合好不好”。

变量筛选与建模

在多元回归前，研究者会用相关系数矩阵查看自变量之间的相关性。
- 高度相关 → 多重共线性风险。
- 低相关 → 变量之间独立性更强，更适合一起放入模型。

Assessing the OLS estimator

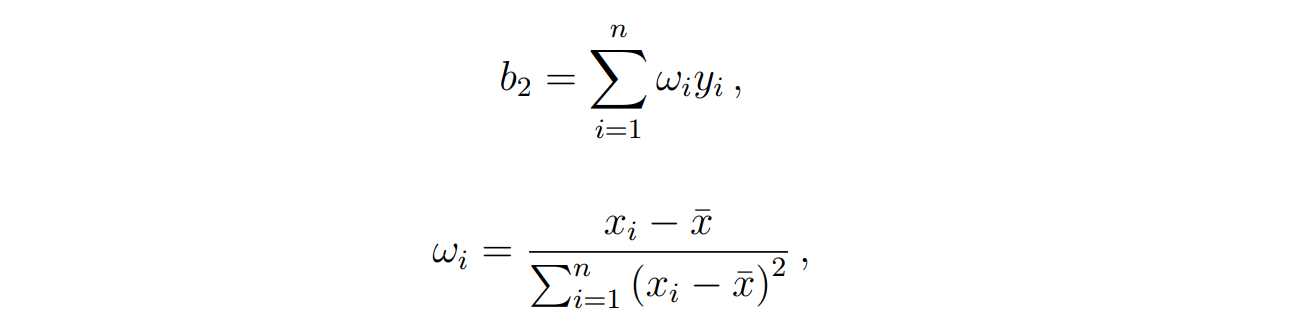
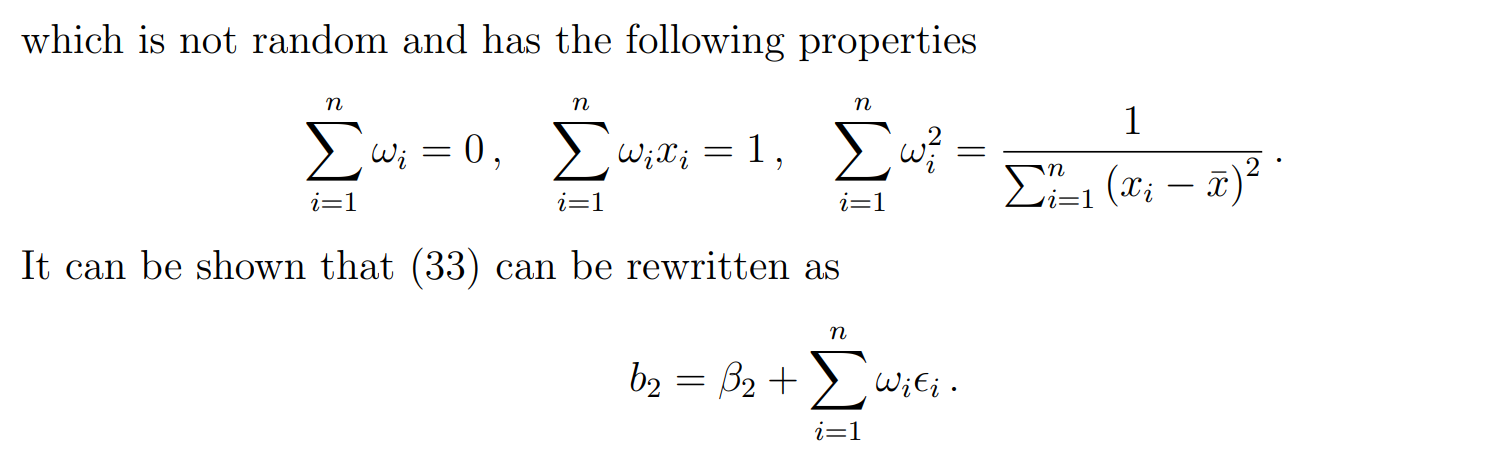
unbiasedness of the estimator

有意思的是:
这里证明无偏是先证明 $b_2$ 再到 $b_1$ ,前面计算最小二乘法是先用 $b_1$ 换元

variance of an estimator

Goodness-of-fit

在一元线性回归中，我们有经典的三分解：

$SST = SSR + SSE$

SST (Total Sum of Squares)：总平方和，度量 y 总的变异性。
SSR (Regression Sum of Squares)：回归平方和，被回归模型解释的那部分变异。
SSE (Error Sum of Squares)：残差平方和，模型没有解释掉的部分。

The Gauss–Markov theorem

这些构造的非 OLS 估计量没法实际拟合，它们的唯一用处就是作为参照物，帮助我们理解为什么 OLS 是 “Best Linear Unbiased Estimator”。

Coefficient of determination(判定系数)

一元回归： $R^2$ 既可以理解为 x 与 y 的相关性平方；
所有回归： $R^2$ 也可以理解为 y 与预测值 $y^\hat{y}$ 的相关性平方；

什么时候减 $y^\hat{y}$ 什么时候减去 $y^ˉ\bar{\hat{y}}$

1. 当 $y^\hat{y}$ 减去 $yˉ\bar{y}$ 的情况

出现在 方差分解 (SST = SSR + SSE) 里。

$SSR=∑i=1n(y^i−yˉ)2SSR = \sum_{i=1}^n (\hat{y}_i - \bar{y})^2$

为什么这里是 $yˉ\bar{y}$ 而不是 $y^ˉ\bar{\hat{y}}$

因为我们在分解的是因变量 y 的总变异性：

$∑(yi−yˉ)2=∑(y^i−yˉ)2+∑(yi−y^i)2\sum (y_i - \bar{y})^2 = \sum (\hat{y}_i - \bar{y})^2 + \sum (y_i - \hat{y}_i)^2$
这里必须用 $yˉ\bar{y}$ ，保证三项加起来正好等于总平方和 SST。
直观理解：我们关心的是回归线解释了多少 y 的变动，而 y的均值才是参照点。

2. 当 $y^\hat{y}$ 减去 $y^ˉ\bar{\hat{y}}$ 的情况

出现在 协方差或相关系数的定义里：

$ry,y^=∑(yi−yˉ)(y^i−y^ˉ)∑(yi−yˉ)2∑(y^i−y^ˉ)2r_{y,\hat{y}} = \frac{\sum (y_i - \bar{y})(\hat{y}_i - \bar{\hat{y}})}{\sqrt{\sum (y_i - \bar{y})^2 \sum (\hat{y}_i - \bar{\hat{y}})^2}}$