运筹学——对偶单纯形法，目标函数系数的敏感性分析

对偶单纯形法

学习这个方法的意义在于有时候，求max的线性规划问题比较复杂，解方程式的过程很繁琐，此时就可以求原线性规划问题max的对偶问题min，换一个思路就可以简单求出，这样的情景下比较实用。

话不多说，从实例中看具体的解法

假设现在有一个线性规划问题如下：

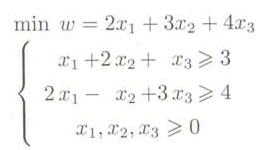
用对偶单纯形法解的过程如下：
我将用尽可能直白的语言描述这个过程，当然了，暂时还不能编成歌词当歌唱 ；）

第一步：写标准型（主要是为了得到对偶问题的初始可行基）
令z=-w，就得到：

为了使约束方程的系数矩阵方便找基阵，就把约束方程引入的两个剩余变量x₄,x₅前面的系数变换为正号，方程的左右两端都同时✖️ -1 ，就得到如下的形式：

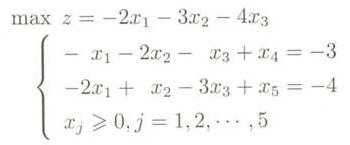
第二步：建单纯形表
（这个知识点忘记的铁子们记得回去复习哦~）

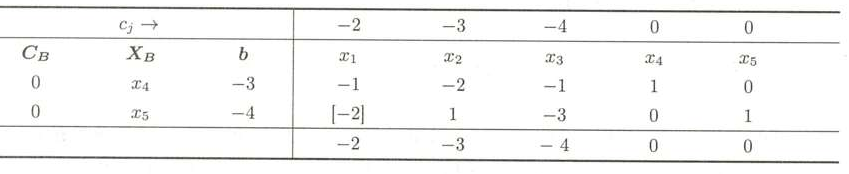
由这个初始单纯形表可知，当前的解是：X=（0,0,0 -3，-4）^T，是基不可行解。

对线性规划问题进行变换后，得到的初始单纯形表中，若检验数λ都是≤0，则对偶问题是基可行解
由于最后一行所有的检验系数都是≤0的，所以检验数行对应的对偶问题的解X’=（-2，-3，-4,0,0）是基可行解。

检验数必须始终保持非正才进行下一步的计算

只有在b对应列的数字中全部都是非负，且检验数全部都是非正时，才得到最优解
又由于b所对应列的数是-3，-4，都是＜0的负数，所以需要进行迭代，将b对应列的数都化为正数才是最优解，所以接下的工作就是-3，-4化为正数。

找出基变量：对比b列中数字，选最小的数，这个数对应的变量就是出基变量
找出基变量：这个例子中，b所对应列的数是-3，-4，最小的是 -4，并且 -4 对应的变量是x₅，所以出基就是x₅.

找入基变量：只看负的，0和正数都不看，用检验数 λ_i / a_ij ，找其中的值最小的，对应的变量就是入基变量
找入基变量：计算检验数λ_i/a_ij,这个表中就是只看X₅对应的行，这一行中0和正数不看，只看负的，所以就有：

（由于正数不计算，且检验数都是负数，所以这里得到的Θ都是正的）

在所有的Θ值中选最小的，就找到了出基变量的行与入基变量的列，它们交叉的位置就是主元素，然后就和之前的单纯形法的步骤一样了，把主元素化为1，主元素所在列的其他元素化为0，这样就得到新的表，再看b列和最后一行数值的正负情况进行判断是否为最优解。
Θ的值有1,4/3，所以选择1，那么1对应的变量x₁就是入基变量，且x₁的列就是入基变量的列，与之前的出基变量的行交叉位置的主元素是 -2 ，接下来就是进行初等行变换，并再算一遍检验数（若检验数行出现正数，就要小心了，或许是算错了，仔细检查一遍）：

这个表中，b对应列的负数只有 -1，那么 -1 所对应的变量x₄就是出基变量，再按照上面的方法计算对应的行的Θ值，就是：

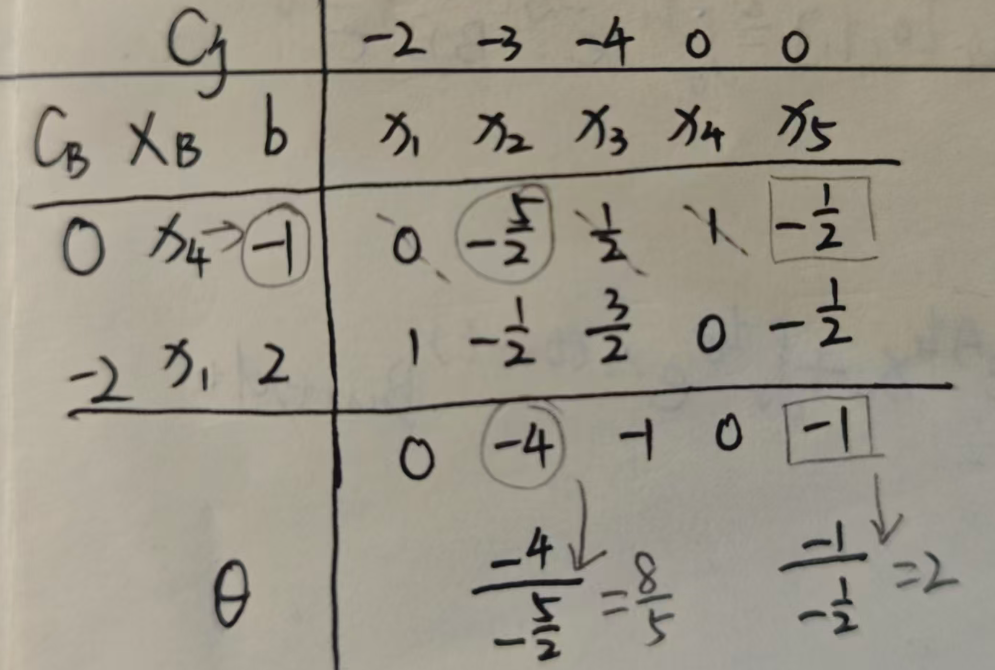
8/5与2，这两个值就选最小的8/5，那么对应的x₂就是入基变量，并且入基变量对应的列与出基变量对应行的交叉位置是 -5/2，所以要做初等行变换，把主元素-5/2化作1，这个列上其它元素化为0，要记得计算检验数，因此就有：

看表发现b对应的列都是正数，且检验数行都是负数，那么这个时候得到的解就是最优解，最优解为：X*=（11/5,2/5,0,0,0）^T。
若对应两个约束条件的对偶变量分别是y₁，y₂，那么对偶问题的最优解就是：Y*=（y₁^*，y₂^*）=（8/5,1/5）

结论
对偶单纯形法的特点
1，初始解可以的非可行解，检验数都是负数时可以进行换基迭代，不必再引入更多的人工变量就能计算。
2，变量个数比约束条件多时，或者变量个数较少，但约束条件很多的线性规划问题，就可以先转变为对偶问题，然后用对偶单纯形法来计算。

线性规划的敏感性分析

实际生活中，所有的数值都不是一成不变的，遇到数值变化的情况时，我们就需要考虑这些变化的数值能否影响最后的结果，具体影响的哪一方面的结果，影响范围是多少，这就是敏感性分析，用在线性规划中就是看对最优解是否有影响，若有，那会有具体什么样的变化，需不需要全部再重新计算？
敏感性分析有很多种分类，比如约束右边项的敏感性分析、目标函数系数的敏感性分析、工艺矩阵系数的敏感性分析、添加新变量的敏感性分析、添加新约束的敏感性分析。

这篇文章中只举例一个方面叙述。

目标函数系数的敏感性分析

我们还拿之前的例子来说明这个情况：

假设在如下的矩阵中，第一行的C_j中c1的数值从 -2 变化为 -2.5：

（也就是这个表中的第一行第一个数字）
此时，我们仔细回想一下刚才的过程，在做初等变换时，第一行的C_j并没有参与到初等变换中，因此，它不影响初等变换的结果，但是在计算检验数时，C_j就参与进来了，所以它影响的是检验数的值，那么怎么影响了呢，计算一下就知道原本检验值是0，更改之后的检验值就是 -0.1，因此发现c1从 -2 变化为 -2.5的过程中检验值是变小了。