【题解】洛谷 P4286 [SHOI2008] 安全的航线 [递归分治]
题面指路:https://www.luogu.com.cn/problem/P4286
1.我自己瞎想
第一眼看到就是懵逼,第二眼想到二分距离。
尝试二分距离 d,然后遍历航线上的点看看能不能满足与陆地的距离大于等于 d。
但又发现这个二分的 check 函数非常复杂,甚至说只要:
怎么合理遍历航线上的点?
解决了上面这个问题,那整道题就解决了。
那看来并不是这样做,考虑从上面的问题入手。
如果我们遍历航线上每一段线段,选它们的中点,再一层层的切半递归。
如果当前中点出来的答案加上线段长度 / 2,都比当前最优答案小,直接剪枝。
因为中点最多能移动线段长度 / 2,而最近的陆地点想离远点也就只能远离线段距离 / 2。
(还有线段长度小到一定值也要剪枝,因为题目精度要求小数点后两位,所以这个值定 1e-3)
大概想一下时间复杂度,递归分治的结束条件是线段长度小于 1e-3。
题目范围 -10,000 到 10,000,所以递归最深能到 ,也就是 24 左右。
而前面我们要遍历每块大陆的每个边界求距离,还要乘航线的线段数。
所以是 ,其中 k 为最大是 24 的常数,可以通过此题。
2.仔细分析
知道怎么遍历航线上的点了,但又怎么求点到每个大陆的距离呢?
首先我们要确定这个点在不在大陆上,如果在大陆内距离就为 0。
我们让这个点朝 y 轴的正方向射出一条射线,如果这条射线与多边形的交点个数为奇数,
那么这个点就在多边形内,反之在外。(读者自证不难)
接下来考虑不在大陆上的点 P 和大陆上的某条线段 AB。
根据 P 的对应方位,可以分成以下三组情况:
(1)P 在 AB 的中间,距离为 P 到 AB 的垂直线段。
(2)P 在 A 的左边,距离为 PA。
(3)P 在 B 的右边,距离为 PB。
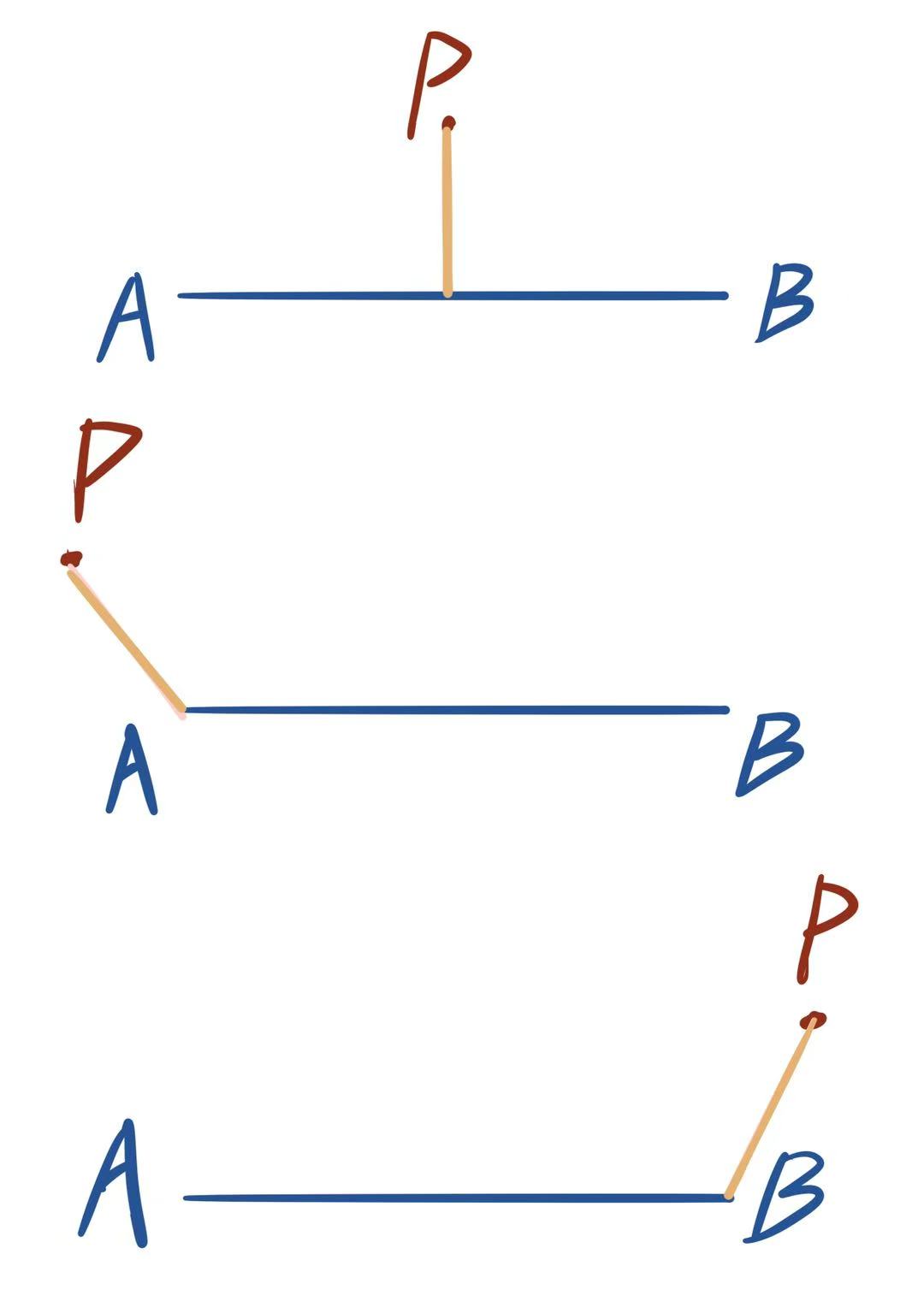
哎呀,这简单,不就用点到直线的距离公式嘛!
激情开打:
#include<bits/stdc++.h>
using namespace std;const int N = 50;
const double eps = 1e-8; //浮点数精度阈值,一般就是题目要求再多六位
int n, c, m[N];struct point {double x, y;
} A[N]; //航线点数组 struct line {point a, b;
} B[N * N]; //大陆边数组
int blen;double ans;double calc_len(point p) {return sqrt( p.x * p.x + p.y * p.y );
}bool equal(double a, double b) { //浮点数判断是否相等 return fabs(a - b) <= eps;
}bool gt(double a, double b) { //浮点数判断是否大于 return a - b > eps;
}// 下面这仨都是重载向量运算符
point operator+(point a, point b) {return {a.x + b.x, a.y + b.y};
}point operator-(point a, point b) {return {a.x - b.x, a.y - b.y};
}double calc_dis(point p, line li) {double xa = li.a.x, ya = li.a.y;double xb = li.b.x, yb = li.b.y;double k = (yb - ya) / (xb - xa);double b = ya - k * xa; if (gt(min(xa, xb), p.x)) { // 如果 p 在 a 的左边return calc_len(li.a - p);}else if(gt(p.x, max(xa, xb))) { // 如果 p 在 b 的右边return calc_len(li.b - p);}else { // p 在 ab 中间 double dis = fabs(k * p.x - p.y + b) / sqrt(1 + k * k);return dis;}
}/*
判断点p是否在陆地上
1. 从点 p 向 y 轴的正方向发射一条射线
2. 统计与多边形边的交点数量
3. 如果交点数量为奇数,则点在多边形内部;否则在外部
如果点 p 不在陆地上 return 0,否则 1
*/
bool check(point p) {int sum = 0;for (int i = 1; i <= blen; i++) {double xa = B[i].a.x, ya = B[i].a.y;double xb = B[i].b.x, yb = B[i].b.y;// 处理与 y 轴平行的线段 if (equal(xa, xb)) {if (equal(xa, p.x)) {return 1; // 点p在线段上}continue; // 不在就直接跳过 }if (gt(p.x, min(xa, xb)) && gt(max(xb, xa), p.x)) { //如果 xa < p.x < x.b double k = (yb - ya) / (xb - xa);double b = ya - k * xa; if (gt(k * p.x + b, p.y)) { // p 在线段上的映射点在 p 点之上// 也就是射线在线段上有交点 sum ++;}}}return sum & 1; // sum 是奇数就返回 1,反之 0
}/*
递归分治算法寻找航线中距离最近陆地最远的点
1. 将航线线段 ab 二分,得到中点 mid
2. 计算中点 mid 到最近陆地线段的距离 dis
3. 如果当前最佳答案 ans 比 dis 加上剩余可能增益还要大,则剪枝
4. 否则递归处理左右两半线段*/
void dfs(point a, point b) {double dis = 1e9, len = calc_len(b - a); //距离和当前航线线段长度 point mid = {(a.x + b.x) / 2, (a.y + b.y) / 2};if (check(mid)) { //如果在大陆上 dis = 0;}else {for (int i = 1; i <= blen; i++) {dis = min(dis, calc_dis(mid, B[i]));// cout << dis << "\n";}}if (gt(ans, dis + len / 2) || len < 1e-3) {return ; }ans = max(ans, dis);dfs(a, mid);dfs(mid, b);
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> c >> n;for (int i = 1; i <= n; i++) {cin >> A[i].x >> A[i].y;}blen = 0;for (int i = 1; i <= c; i++) { //把所有大陆的边放到 a 里面 cin >> m[i];point fir, pre;cin >> fir.x >> fir.y;pre = fir;for (int j = 2; j <= m[i]; j++) { //单个大陆的边连一起 point p;cin >> p.x >> p.y;blen ++;B[blen] = {pre, p};pre = p;}blen ++;B[blen] = {pre, fir}; //当前大陆的第一个点和最后一个点 }ans = 0;for (int i = 1; i < n; i++) {dfs(A[i], A[i + 1]); //递归分治航线上的每段边 }cout << fixed << setprecision(2) << ans;return 0;
}一交上去只有 50 分。。。而且错误数据答案都偏大。
检查发现还有线段与 y 轴平行的情况没考虑,如果近似平行的话:
这个 k 的分母就会无限小,这个就无限大,算出来的 dis 也很大。
(而且除以 0 会 RE)
那么我们精心设计的:
if (gt(ans, dis + len / 2) || len < 1e-3) {return ; }这个剪枝的前半部分就会因为 dis 巨大而无法起作用,可能超时。
修改 dis 函数:
double calc_dis(point p, line li) {double xa = li.a.x, ya = li.a.y;double xb = li.b.x, yb = li.b.y;if (equal(xa, xb)) { // 如果线段与 y 轴垂直 if (gt(min(ya, yb), p.y)) { // 如果 p 在 a 的下边return calc_len(li.a - p);}else if(gt(p.y, max(ya, yb))) { // 如果 p 在 b 的上边return calc_len(li.b - p);}else {return fabs(p.x - xa); // p 在 ab 中间 }}double k = (yb - ya) / (xb - xa);double b = ya - k * xa; if (gt(min(xa, xb), p.x)) { // 如果 p 在 a 的左边return calc_len(li.a - p);}else if(gt(p.x, max(xa, xb))) { // 如果 p 在 b 的右边return calc_len(li.b - p);}else { // p 在 ab 中间 double dis = fabs(k * p.x - p.y + b) / sqrt(1 + k * k);return dis;}
}线段与 y 轴平行的情况有三种,还得分开考虑,代码更长了。
交上去发现得了 60 分。。
到底还有哪里有问题呢?
其实还是与 y 轴平行线段的锅,我们判断平行的精度是 1e-8。
那么 的
最大就可以去到 1e7 级别。
除一个这么大的数,会让精度大大损失,从而导致答案偏差,俗称精度问题。
那应该怎么改呢?
如果你学过半平面交,就知道这个时候我们要使用向量了。
3.点积及运用
这里有两个向量:
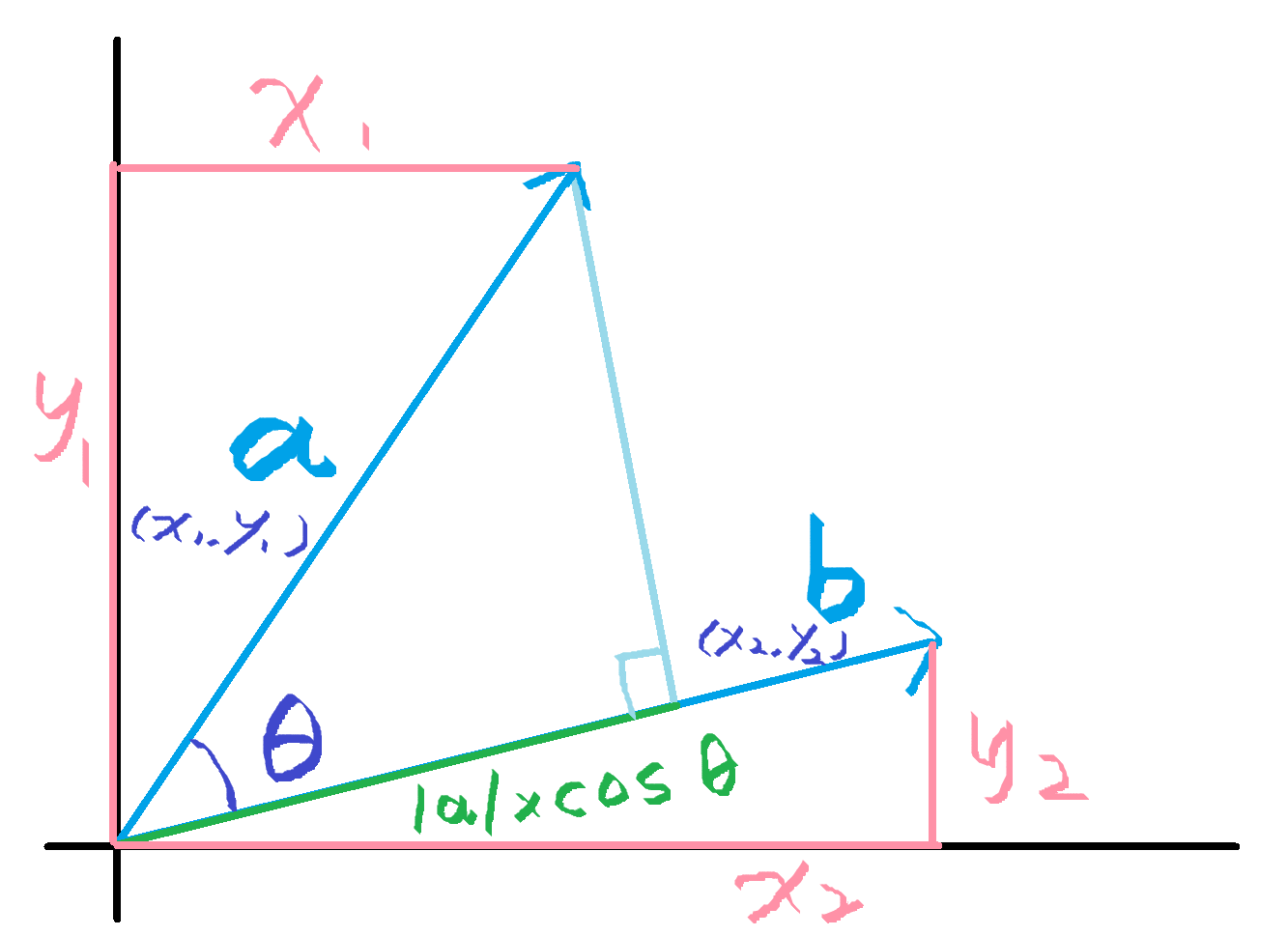
定义两个向量的点积为:
同时几何定义里也可以这么表示:
(其中 为向量
的模长,
为两向量的夹角)
和叉积不同,点积的计算结果是一个标量(数值)而非向量。
关于这个 和这个
为什么相等,需要用到余弦定理:
考虑由
、
和
构成的三角形,满足:
(下面就是余弦定理的百度百科,我懒得写了)
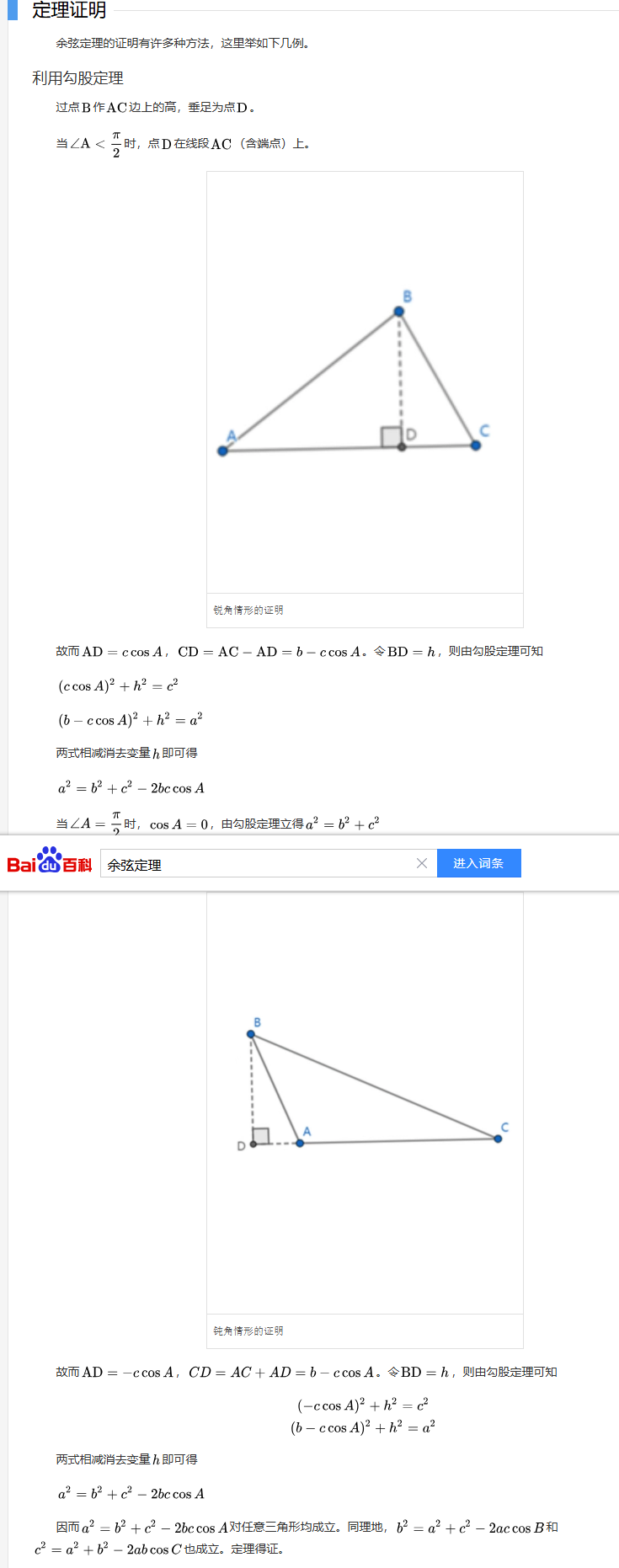
把这个式子的左边展开:
那么就有:
所以:
知道这个有啥用呢?
回到我们的点 P 和线段 AB,如果 P 在 AB 中间:
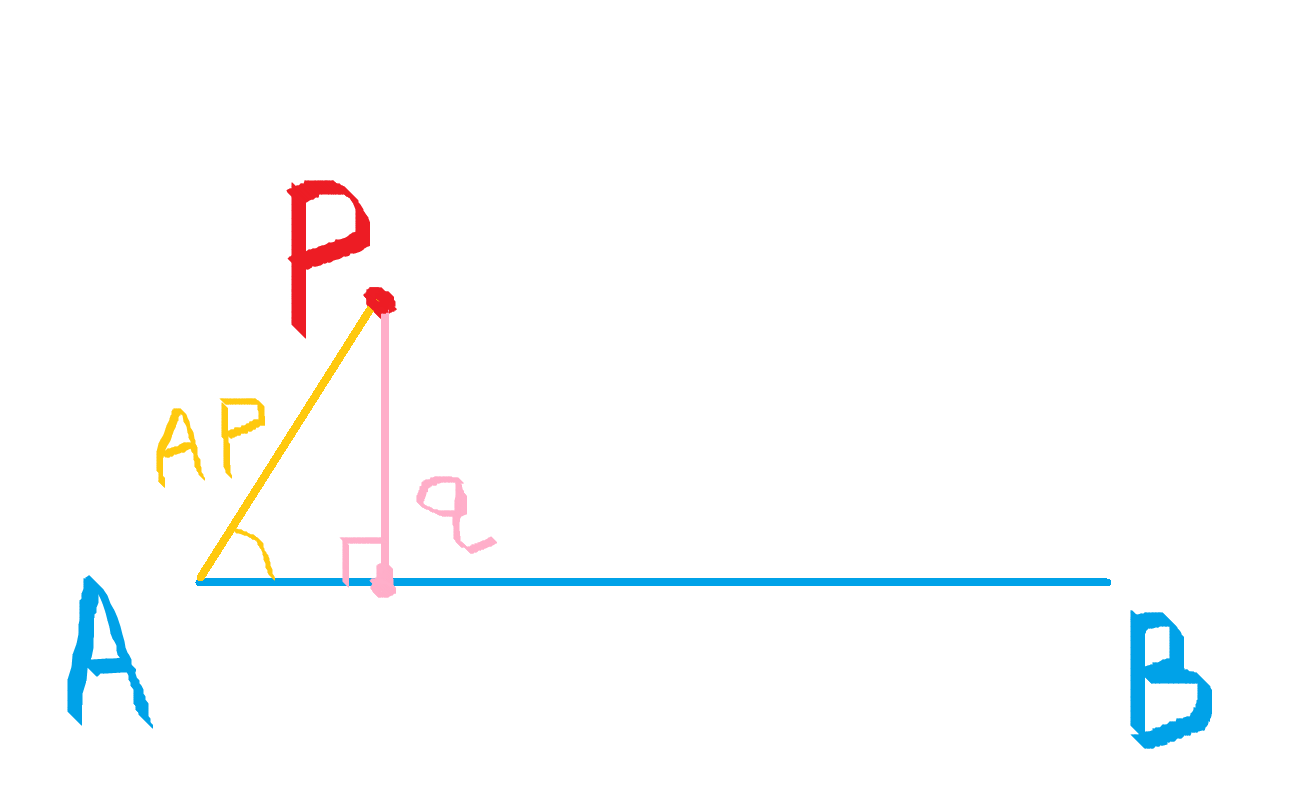
我们只要求出 P 在 AB 上的投影点 q,再求出 Pq 的长度就是距离。
考虑 AP 和 AB 的点积,,其中
就是 Aq 的长度。
那么只要求出 Aq 的长度与 AB 长度的比值 t,就可以进一步求出 Pq。
再看看其他两种情况:
P 在 A 的左边,距离为 PA。
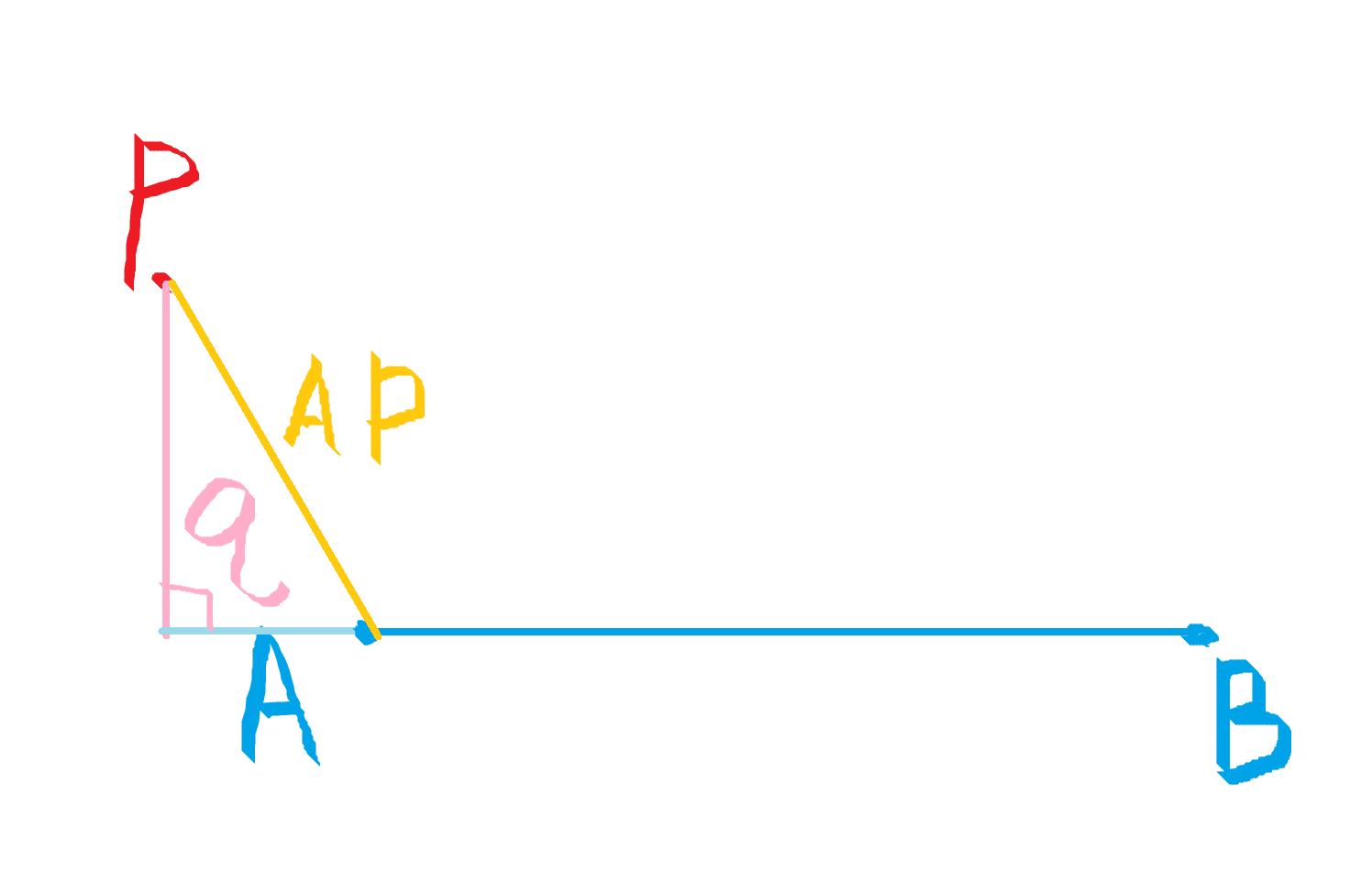
很明显,这里 是个负数,
也是个负数。
那只要特判比值 是不是负数,如果是就直接输出
。
P 在 B 的右边,距离为 PB。
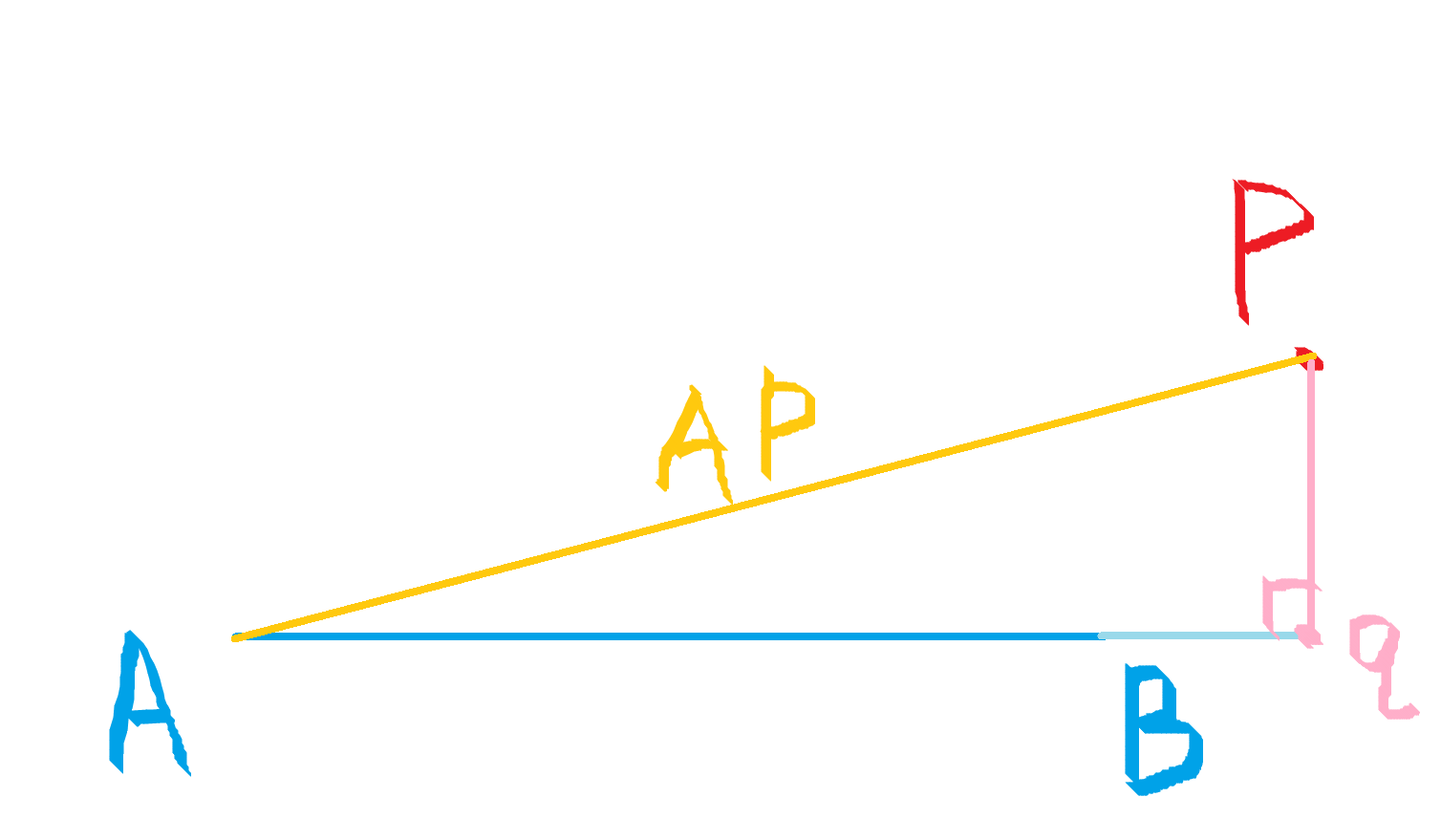
这里的 ,所以
大于 1。
那只要特判比值 是不是大于 1,如果是就直接输出
。
4.正确代码
对比之前的只改了 dis 函数和加了个点积重载:
#include<bits/stdc++.h>
using namespace std;const int N = 50;
const double eps = 1e-8; //浮点数精度阈值,一般就是题目要求再多六位
int n, c, m[N];struct point {double x, y;
} A[N]; //航线点数组 struct line {point a, b;
} B[N * N]; //大陆边数组
int blen;double ans;double calc_len(point p) {return sqrt( p.x * p.x + p.y * p.y );
}bool equal(double a, double b) { //浮点数判断是否相等 return fabs(a - b) <= eps;
}bool gt(double a, double b) { //浮点数判断是否大于 return a - b > eps;
}// 下面这仨都是重载向量运算符
point operator+(point a, point b) {return {a.x + b.x, a.y + b.y};
}point operator-(point a, point b) {return {a.x - b.x, a.y - b.y};
}double operator*(point a, point b) { //点积 return a.x * b.x + a.y * b.y;
}double calc_dis(point p, line li) {point a = li.a, b = li.b;point ap = p - a, ab = b - a, bp = p - b;double t = ap * ab / (ab.x * ab.x + ab.y * ab.y); // 计算投影比例 t = (ap·ab)/|ab|^2if (t < -eps) // 投影点在 a 点左侧return calc_len(ap);if (t - 1 > eps) // 投影点在 b 点右侧return calc_len(bp);// 投影点 q 在线段 ab上point pp = {ab.x * t, ab.y * t};point q = a + pp; return calc_len(p - q);
}/*
判断点 p 是否在陆地上
1. 从点 p 向 y 轴的正方向发射一条射线
2. 统计与多边形边的交点数量
3. 如果交点数量为奇数,则点在多边形内部;否则在外部
如果点 p 不在陆地上 return 0,否则 1
*/
bool check(point p) {int sum = 0;for (int i = 1; i <= blen; i++) {double xa = B[i].a.x, ya = B[i].a.y;double xb = B[i].b.x, yb = B[i].b.y;// 处理与 y 轴平行的线段 if (equal(xa, xb)) {if (equal(xa, p.x)) {return 1; // 点p在线段上}continue; // 不在就直接跳过 }if (gt(p.x, min(xa, xb)) && gt(max(xb, xa), p.x)) { //如果 xa < p.x < x.b double k = (yb - ya) / (xb - xa);double b = ya - k * xa; if (gt(k * p.x + b, p.y)) { // p 在线段上的映射点在 p 点之上// 也就是射线在线段上有交点 sum ++;}}}return sum & 1; // sum 是奇数就返回 1,反之 0
}/*
递归分治算法寻找航线中距离最近陆地最远的点
1. 将航线线段 ab 二分,得到中点 mid
2. 计算中点 mid 到最近陆地线段的距离 dis
3. 如果当前最佳答案 ans 比 dis 加上剩余可能增益还要大,则剪枝
4. 否则递归处理左右两半线段*/
void dfs(point a, point b) {double dis = 1e9, len = calc_len(b - a); //距离和当前航线线段长度 point mid = {(a.x + b.x) / 2, (a.y + b.y) / 2};if (check(mid)) { //如果在大陆上 dis = 0;}else {for (int i = 1; i <= blen; i++) {dis = min(dis, calc_dis(mid, B[i]));// cout << dis << "\n";}}if (gt(ans, dis + len / 2) || len < 1e-3) {return ; }ans = max(ans, dis);dfs(a, mid);dfs(mid, b);
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> c >> n;for (int i = 1; i <= n; i++) {cin >> A[i].x >> A[i].y;}blen = 0;for (int i = 1; i <= c; i++) { //把所有大陆的边放到 a 里面 cin >> m[i];point fir, pre;cin >> fir.x >> fir.y;pre = fir;for (int j = 2; j <= m[i]; j++) { //单个大陆的边连一起 point p;cin >> p.x >> p.y;blen ++;B[blen] = {pre, p};pre = p;}blen ++;B[blen] = {pre, fir}; //当前大陆的第一个点和最后一个点 }ans = 0;for (int i = 1; i < n; i++) {dfs(A[i], A[i + 1]); //递归分治航线上的每段边 }cout << fixed << setprecision(2) << ans;return 0;
}