集成学习：从理论到实践的全面解析

集成学习：从理论到实践的全面解析

摘要：本文深入浅出地讲解集成学习（Ensemble Learning）的核心思想、主流算法及其实际应用。我们将从 Bagging 与 Boosting 的基本概念出发，重点剖析随机森林、AdaBoost、GBDT 和 XGBoost 的原理与实现，并通过多个真实案例展示其强大性能。无论你是机器学习初学者，还是希望系统梳理集成学习知识的开发者，本文都将为你提供一份清晰、实用的指南。

---

一、什么是集成学习？

集成学习（Ensemble Learning）是一种“集思广益”的机器学习思想。它不追求单个模型的极致，而是通过组合多个“弱学习器”（Weak Learners），形成一个更强大的“强学习器”，从而提升整体预测的准确性与稳定性。

正如中国古话所说：“三个臭皮匠，赛过诸葛亮”。在机器学习中，多个表现平平的模型联合起来，往往能超越单一的复杂模型。

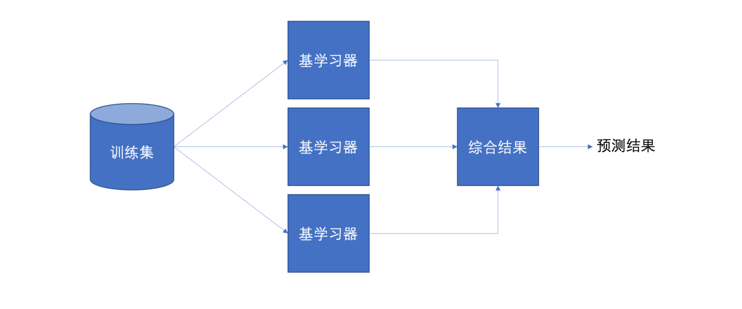
核心思想：

• 训练阶段：使用训练集训练多个弱学习器（如决策树）。
• 预测阶段：对新样本，让所有弱学习器进行预测，再通过投票或加权等方式得出最终结果。

---

二、集成学习的两大流派：Bagging vs Boosting

集成学习主要分为两类：Bagging 和 Boosting。它们在数据处理、训练方式和模型结合策略上存在显著差异。

特性	Bagging	Boosting
数据方面	有放回抽样，生成不同训练子集	使用全部数据，但样本权重动态调整
投票方式	平权投票（多数表决）	加权投票（性能好的模型权重更大）
学习顺序	并行训练，模型间无依赖	串行训练，后一个模型关注前一个的不足

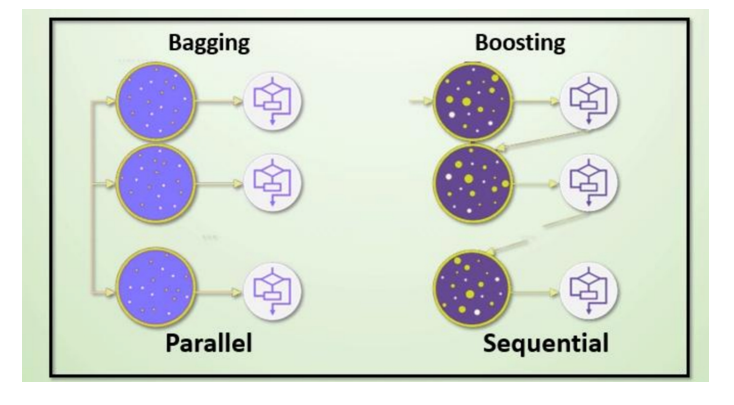
Bagging：随机森林
Boosting：Adaboost、GBDT、XGBoost、LightGBM

---

三、随机森林（Random Forest）

3.1 算法思想

随机森林是基于 Bagging 思想 的集成算法，其基学习器为 决策树。它通过两个“随机性”来增强模型的泛化能力：

1. 样本随机：从原始数据中有放回地抽取样本（Bootstrap）。
2. 特征随机：每次分裂节点时，只从随机选取的特征子集中选择最优分裂特征。

这两个随机性确保了每棵树的独立性，避免了过拟合。

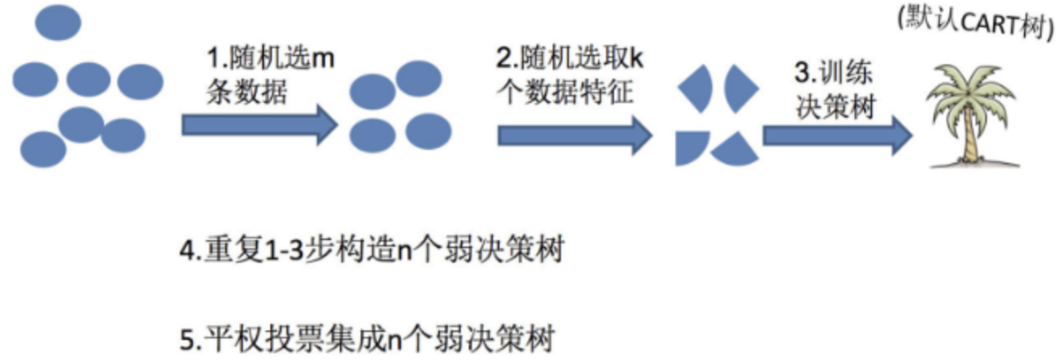
3.2 构建步骤

1. 有放回地抽取多个样本子集。
2. 对每个子集随机选择特征，构建决策树（通常不剪枝）。
3. 所有树构建完成后，对分类任务采用 多数表决，对回归任务采用 平均值 输出最终结果。

3.3 为什么需要随机抽样？

• 有放回抽样：保证每棵树的训练集有重叠，但又不完全相同，增加多样性。
• 若不随机抽样，所有树训练数据一致，最终模型将完全相同，失去集成意义。
  为什么要有放回地抽样？

3.4 为什么要有放回地抽样？

• 如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是“有偏的”，也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决。
• 综上：弱学习器的训练样本既有交集也有差异数据，更容易发挥投票表决效果

3.5 Scikit-learn 实现

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report# 加载数据（以泰坦尼克号为例）
titanic = pd.read_csv("data/train.csv")
X = titanic[['Pclass', 'Age', 'Sex']]
y = titanic['Survived']# 数据预处理
X['Age'].fillna(X['Age'].mean(), inplace=True)
X = pd.get_dummies(X)# 划分训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=22)# 训练随机森林
rfc = RandomForestClassifier(n_estimators=100, max_depth=6, random_state=9)
rfc.fit(X_train, y_train)# 预测与评估
y_pred = rfc.predict(X_test)
print("随机森林准确率:", rfc.score(X_test, y_test))
print(classification_report(y_test, y_pred))

---

四、AdaBoost

4.1 算法思想

AdaBoost（Adaptive Boosting）是一种自适应提升算法，其核心是：

• 关注难分样本：每轮训练后，提高被错分样本的权重。
• 器重好模型：分类误差小的弱学习器在最终投票中拥有更大权重。

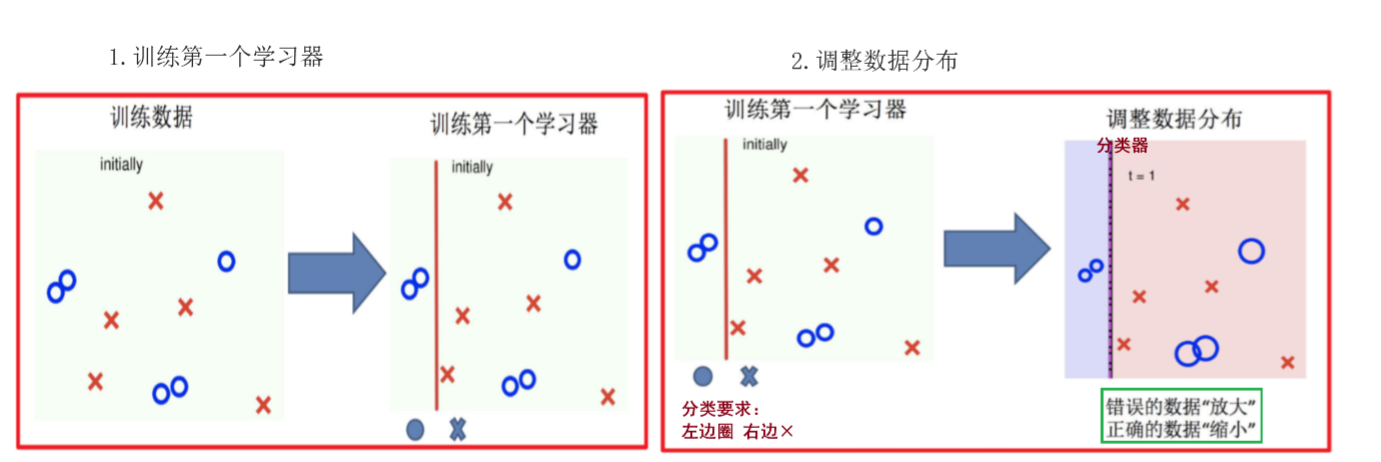
4.2 核心步骤

1. • 初始化所有样本权重相等，训练第 1 个学习器。
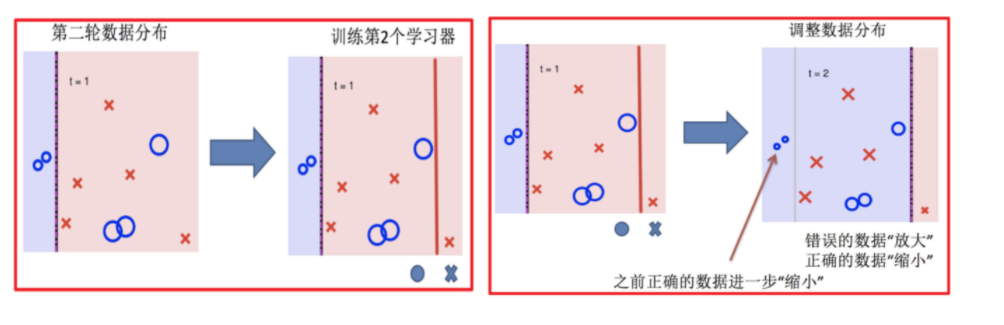
2. • 根据新权重的样本集 训练第 2 个学习器
   • 根据预测结果找一个错误率最小的分裂点计算、更新：样本权重、模型权重。
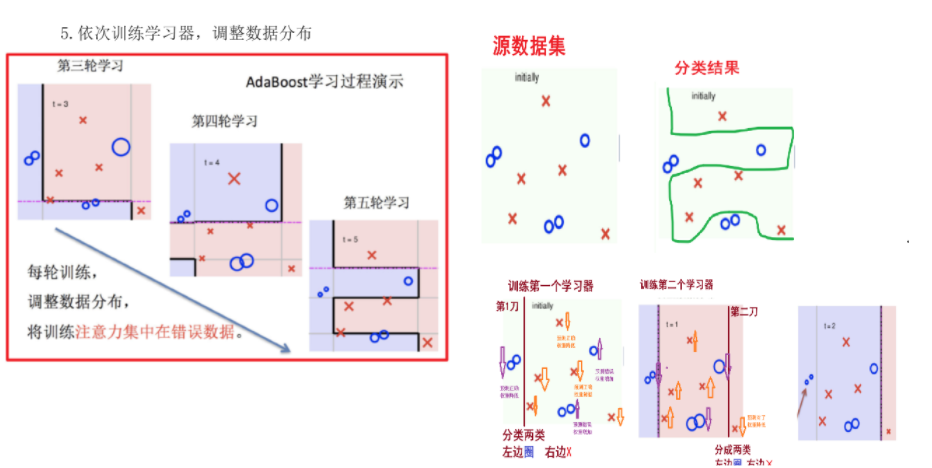
3. • 迭代训练在前一个学习器的基础上，根据新的样本权重训练当前学习器
   • 直到训练出 m 个弱学习器。
4. m 个弱学习器集成预测公式：
   • $H(x)=\text{sign}\left({\sum }_{i=1}^m{a}_i{h}_i(x)\right)$
   • α 为模型的权重，输出结果大于 0 则归为正类，小于 0 则归为负类。
5. 模型权重计算公式:
   • $a_t=\frac{1}{2}\ln \left(\frac{1-{\epsilon }_t}{{\epsilon }_t}\right)$ 为模型权重
   • ${\epsilon }_t$表示第 t 个弱学习器的错误率
6. 样本权重计算公式:
   $$D_{t+1}(x)=\frac{D_t(x)}{Z_t}\times \{\begin{array}{ll}{e}^{-a_t},& \text{预测值 = 真实值}\\ e^{a_t},& \text{预测值 }\ne \text{ 真实值}\end{array}$$
   • 其中 $Z_t$ 为归一化值（所有样本权重总和）
   • $D_t(x)$ 为样本权重
   • $a_t$ 为模型权重
     
     
     

4.3 实战：葡萄酒分类

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier# 使用单层决策树作为基学习器
base_estimator = DecisionTreeClassifier(criterion='entropy', max_depth=1)
ada = AdaBoostClassifier(base_estimator=base_estimator, n_estimators=500, learning_rate=0.1, random_state=0)# 训练与评估
ada.fit(X_train, y_train)
y_pred = ada.predict(X_test)
print("AdaBoost 准确率:", accuracy_score(y_test, y_pred))

结果分析：AdaBoost 通常能显著提升弱分类器的性能，且在训练集上表现优异，但需注意过拟合风险。

---

五、梯度提升树：GBDT

5.1 提升树思想

GBDT（Gradient Boosting Decision Tree）是 Boosting 的进阶版本。它不再简单地“纠正错误”，而是通过拟合残差来逐步优化模型。

类比：预测一个人的年龄。先用20岁预测，误差10岁；再用6岁预测误差，剩下4岁；再用3岁预测，误差仅1岁……最终将所有预测相加。

5.2 梯度提升的核心

GBDT 使用损失函数的负梯度来代替残差，适用于各种损失函数（如平方损失、LogLoss）。

假设：

1. 前一轮迭代得到的强学习器是： $f_{t-1}(x)$
2. 损失函数为平方损失是： $L(y,f_{t-1}(x))$
3. 本轮迭代的目标是找到一个弱学习器：$h_t(x)$
4. 让本轮的损失最小化：
   $$L(y,f_t(x))=L(y,f_{t-1}(x)+h_t(x))=(y-f_{t-1}(x)-h_t(x){)}^2$$
5. 则要拟合的负梯度为：
   $$\frac{\partial L(y,f(x_i))}{\partial f(x_i)}=f(x_i)-y_i$$
   $$-\left[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}\right]=y_i-f(x_i)$$

• 回归问题：负梯度 ≈ 残差
• 分类问题：负梯度 = LogLoss 的梯度

5.3 算法流程

1. 初始化模型（如所有样本预测为均值）。
2. 计算当前模型的负梯度（即残差）。
3. 训练一个CART树来拟合这些残差。
4. 更新模型：F(x) = F_prev(x) + 学习率 * 新树预测值
5. 重复2-4步，直到达到指定树的数量。

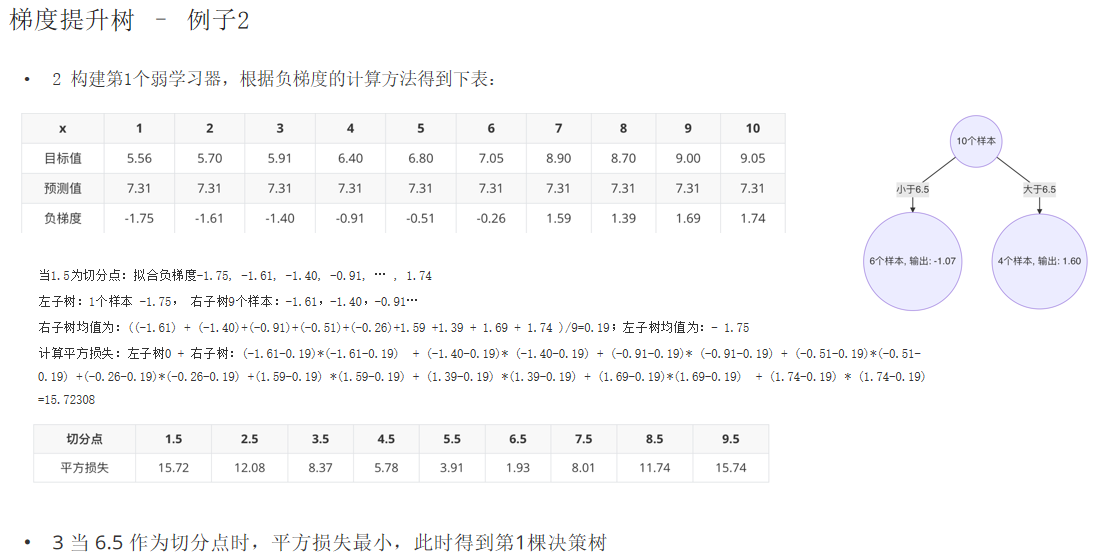
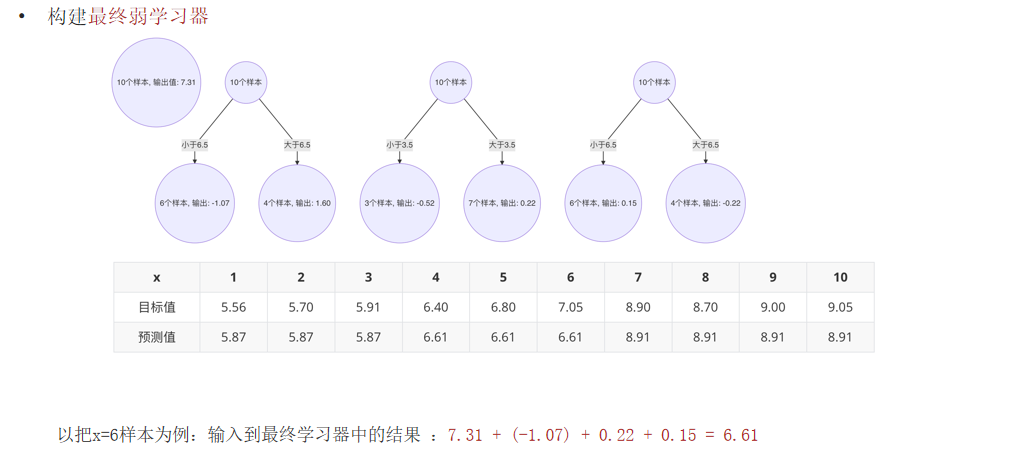
案例

5.4 Scikit-learn 实现

from sklearn.ensemble import GradientBoostingClassifiergbc = GradientBoostingClassifier(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=22)
gbc.fit(X_train, y_train)
y_pred = gbc.predict(X_test)
print("GBDT 准确率:", gbc.score(X_test, y_test))

---

六、XGBoost：极致的梯度提升

6.1 XGBoost 的优势

XGBoost（Extreme Gradient Boosting）是 GBDT 的高效实现，广泛应用于 Kaggle 竞赛。其改进点包括：

• 二阶泰勒展开：更精确地逼近损失函数。
• 正则化项：控制树的复杂度，防止过拟合。
• 自定义分裂指标：从目标函数直接推导出最优分裂点。

6.2 目标函数

XGBoost 的目标函数由两部分组成：

Obj = ΣL(y, y_pred) + ΣΩ(f_k)

其中：

• L 是损失函数（如交叉熵、平方误差）
• Ω(f_k) = γT + λ||w||² 是正则项
  • T：叶子节点数
  • w：叶子节点的预测值
  • γ, λ：正则化系数

6.3 树的构建

XGBoost 使用“打分函数”（Gain）来决定是否分裂：

Gain = 1/2 * [ (G_L²/(H_L+λ) + G_R²/(H_R+λ) - (G_L+G_R)²/(H_L+H_R+λ)) ] - γ

若 Gain > 0，则分裂；否则停止。

6.4 Python 实现

import xgboost as xgb
from sklearn.model_selection import GridSearchCV# 基础训练
estimator = xgb.XGBClassifier(n_estimators=100,max_depth=3,learning_rate=0.1,objective='multi:softmax',eval_metric='merror',use_label_encoder=False,random_state=22
)
estimator.fit(X_train, y_train)# 超参数调优
param_grid = {'max_depth': [3, 4, 5],'n_estimators': [50, 100, 150],'learning_rate': [0.05, 0.1, 0.15]
}
cv = GridSearchCV(estimator, param_grid, cv=5)
cv.fit(X_train, y_train)
print("最优参数:", cv.best_params_)

---

七、总结与对比

算法	类型	特点	适用场景
随机森林	Bagging	并行训练，抗过拟合，易于调参	分类、回归，通用性强
AdaBoost	Boosting	串行训练，关注难分样本，对噪声敏感	弱分类器提升
GBDT	Boosting	拟合残差，性能强，训练较慢	结构化数据预测
XGBoost	Boosting	二阶优化，正则化，速度快，精度高	竞赛、工业级应用

---

八、结语

集成学习是机器学习中的“瑞士军刀”，它通过组合多个模型，显著提升了预测性能。无论是随机森林的“民主投票”，还是 XGBoost 的“梯度优化”，都体现了“团结就是力量”的智慧。

掌握这些算法，不仅能提升你的模型性能，更能加深对机器学习本质的理解。建议动手实践本文中的案例，从代码中感受集成学习的魅力！

---