集成学习简介

集成学习介绍

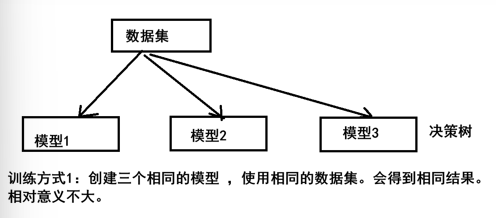
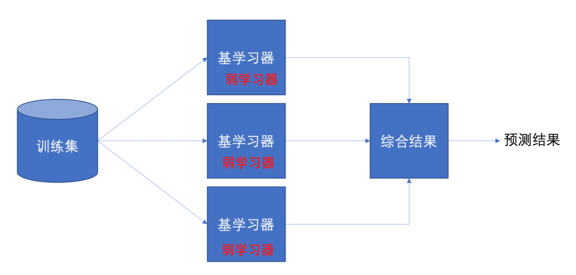
集成学习是机器学习中的一种思想，它通过多个模型的组合形成一个精度更高的模型，参与组合的模型成为弱学习器（弱学习器）。训练时，使用训练集依次训练出这些弱学习器，对未知的样本进行预测时，使用这些弱学习器联合进行预测

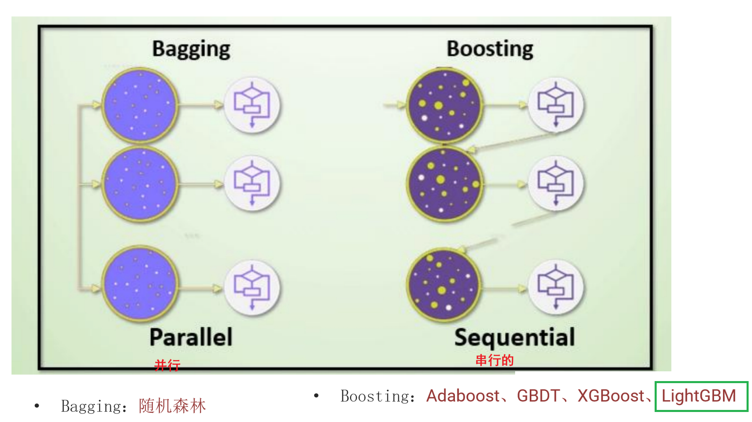
主要学两种思想：Bagging和boosting

集成学习：

bagging

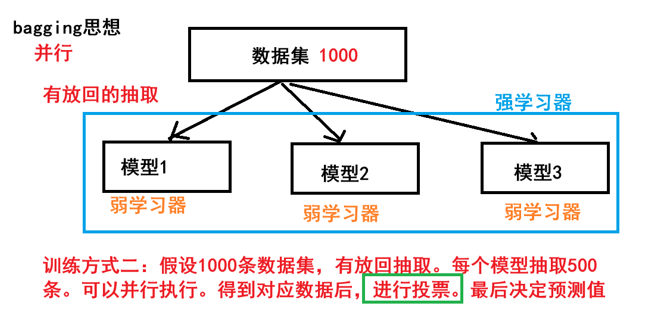
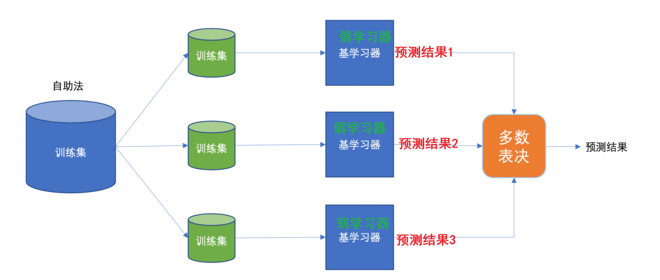
有放回的抽样(bootstrap抽样)产生不同的训练集，从而训练不同的学习器

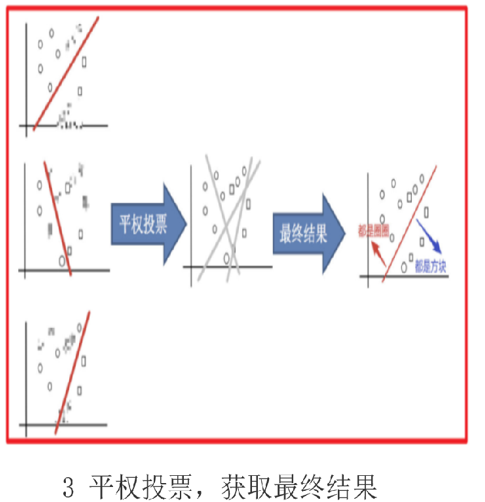
通过平权投票、多数表决的方式决定预测结果

弱学习器可以并行训练

例：

分类圈和方块

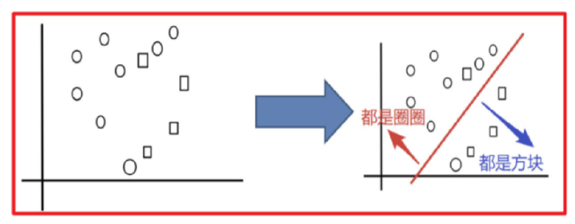
打码的图像表示此次未被抽取

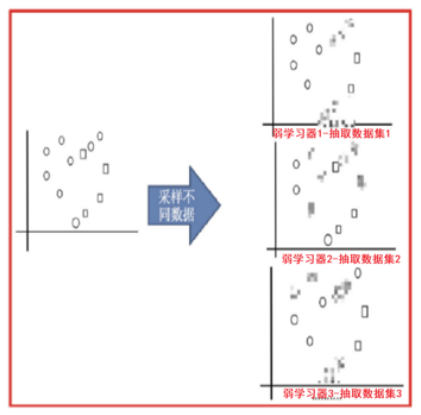
抽取三个训练集训练分类器之后会有三个不同的分类结果

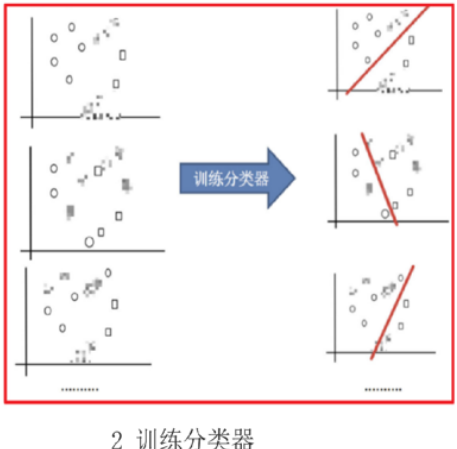
boosting

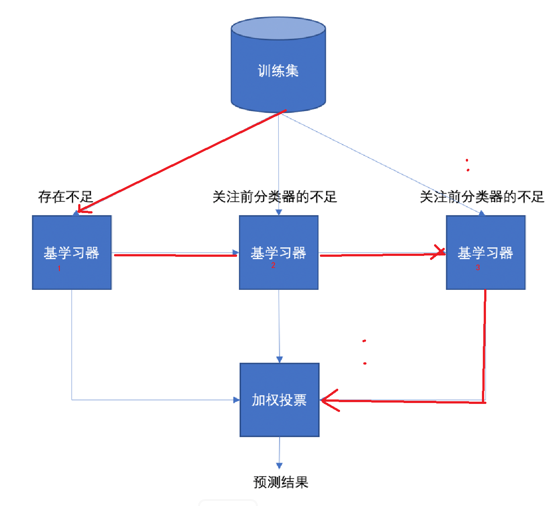
每一个训练器重点关注前一个训练器不足的地方进行训练

通过加权投票的方式，得出预测结果

串行的训练方式

随着学习的积累从弱到强

每新加入一个弱学习器，整体能力就会得到提升

代表算法：Adaboost，GBDT，XGBoost，LightGBM

随机森林算法

随机森林是基于 Bagging 思想实现的一种集成学习算法，采用决策树模型作为每一个弱学习器

步骤示意

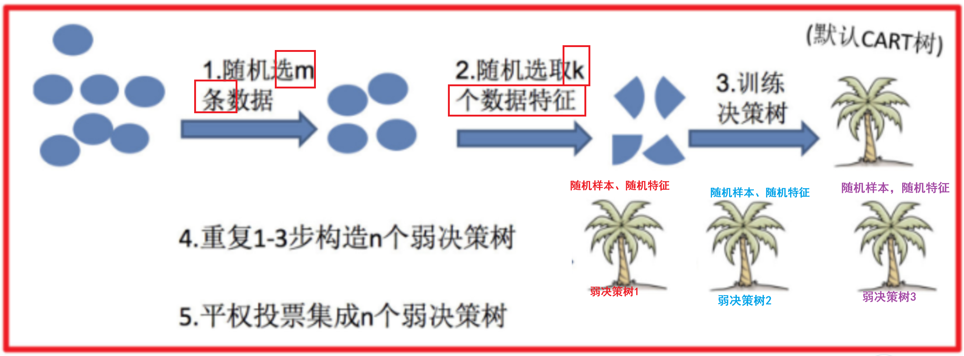
如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是“有偏的”，也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决。

综上：弱学习器的训练样本既有交集也有差异数据，更容易发挥投票表决效果

"""案例：演示   集成学习之bagging思想   随机森林算法代码集群学习：概述:把多个弱学习器， 组成1个强学习的过程 -》集成学习思想：bagging思想：1：有放回的随机抽样2：平权投票3：可以并行执行boosting思想：1：每次训练更关注上一个学习器异常数据2：加权投票-> 预测正确：权重降低  预测错误：权重增加3：串行执行bagging思想代表算法：随机森林算法、随机森林算法：1：每个弱学习器都是CART树（必须是二叉树）2：有放回的随机抽样 ，平权投票、并行执行
"""
#导包
import pandas as pd
from sklearn.model_selection import  train_test_split
from sklearn.tree import  DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier  #随机森林算法 （分类器）
from sklearn.model_selection import GridSearchCV  #网格搜索#1、获取数据
df=pd.read_csv("../data/train.csv")
df.info()
#2、数据预处理
#2.1 抽取特征 和标签
x=df[['Pclass','Sex','Age','Fare','SibSp']].copy()
y=df['Survived']#2.2空值处理
x['Age']=x['Age'].fillna(x['Age'].mean())#2.3热编码处理
x=pd.get_dummies(x)#2.4 划分数据集  训练集和测试集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=22)
#3、特性工程  略
#4、模型训练    预测    评估
#场景1：单1决策树
#4.1 创建决策树对象  演示：单一决策树
es1=DecisionTreeClassifier()
#4.2训练
es1.fit(x_train,y_train)
#4.3预测
y_pre = es1.predict(x_test)
#4.4评估
print(f"单一决策树的模型准确率:{es1.score(x_test,y_test)}")
print("*"*22)#场景2：随机森林算法 -》 默认参数
#4.1 创建随机森林对象  默认 多个决策树(baggding思想)
# 弱学习器个数 有！！ 使用默认的！！！ 100个   深度
es2=RandomForestClassifier(n_estimators=60,max_depth=7)
#4.2 模型训练
es2.fit(x_train,y_train)
#4.3预测
y_pre2=es2.predict(x_test)
print(f"随机森林的模型准确率:{es2.score(x_test,y_test)}")
print("*"*22)#场景3：随机森林算法 ->采用网格搜索
#4.1创建随机森林对象
es3=RandomForestClassifier()
#4.2 准备参数  构建网格搜索
params={'n_estimators':[30,50,60,90,110],'max_depth':[2,3,5,7,9]
}
#4.3寻找超参
gs_es = GridSearchCV(es3,param_grid=params,cv=4)
#4.4模型训练
gs_es.fit(x_train,y_train)
#4.5预测
y_pre3=gs_es.predict(x_test)
print(f"随机森林的模型准确率:{gs_es.score(x_test,y_test)}")
#4.6寻找最佳参数
print(f"最佳参数:{gs_es.best_params_}")

Adaboost算法

Adaptive Boosting(自适应提升)基于 Boosting思想实现的一种集成学习算法核心思想是通过逐步提高那些被前一步分类错误的样本的权重来训练一个强分类器

流程如：

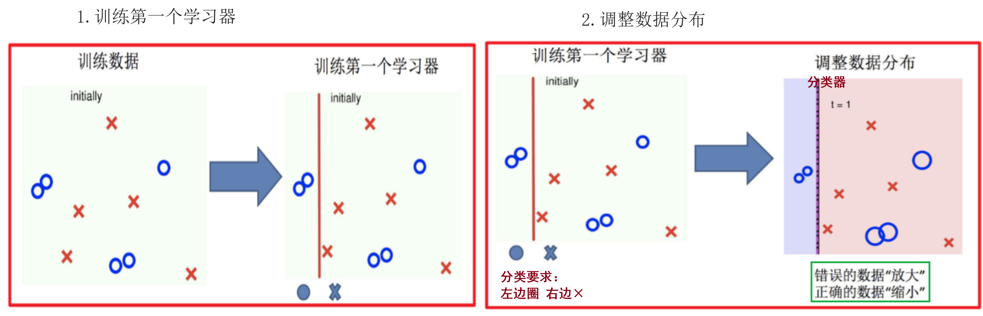
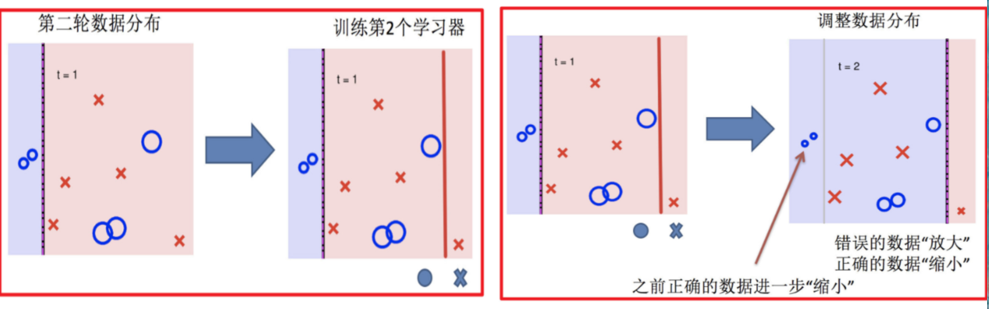
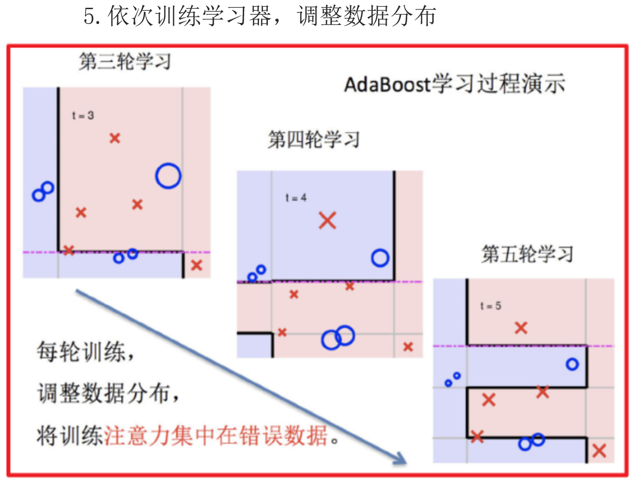
adaboost算法推导

1 初始化训练数据权重相等，训练第 1 个学习器

如果有 100 个样本，则每个样本的初始化权重为：1/100

根据预测结果找一个错误率最小的分裂点，计算、更新：样本权重、模型权重

2 根据新权重的样本集 训练第 2 个学习器

根据预测结果找一个错误率最小的分裂点计算、更新：样本权重、模型权重

3 迭代训练在前一个学习器的基础上，根据新的样本权重训练当前学习器

        直到训练出 m 个弱学习器

4  m 个弱学习器集成预测公式：

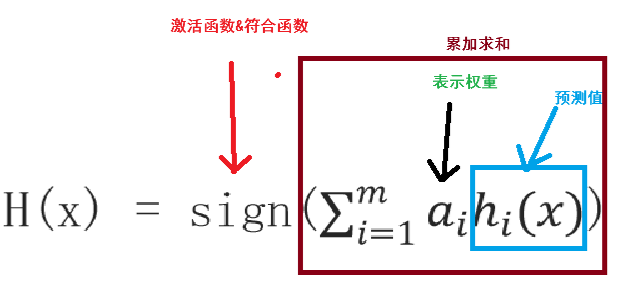
α 为模型的权重，输出结果大于 0 则归为正类，小于 0 则归为负类

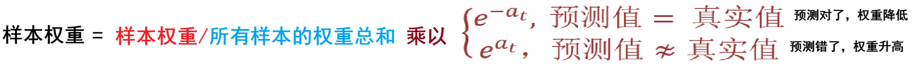
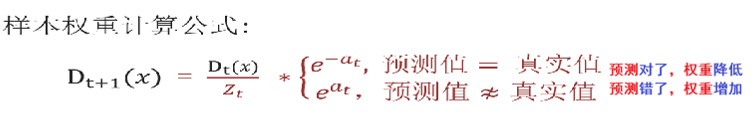
来个示例：

已知训练数据见下面表格，假设弱分类器由 x 产生，预测结果使该分类器在训练数据集上的分类误差率最低，试用 Adaboost 算法学习一个强分类器

构建第一个分类器

每个样本权重为0.1

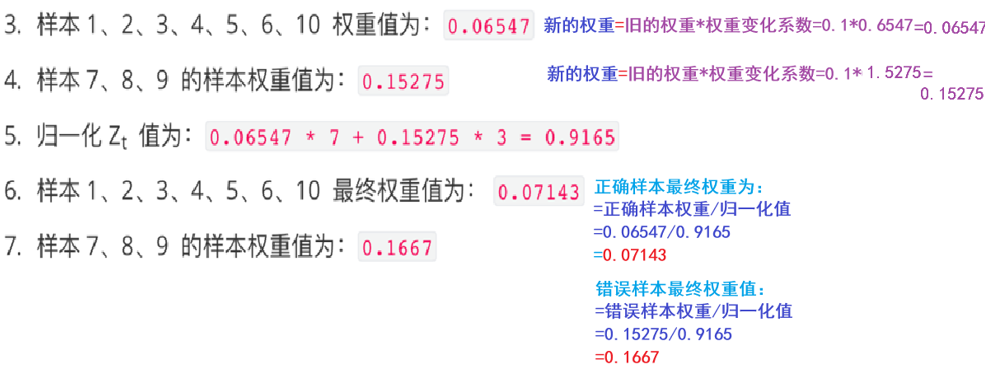
然后再以第一次得到的权重再去训练第二个分类器

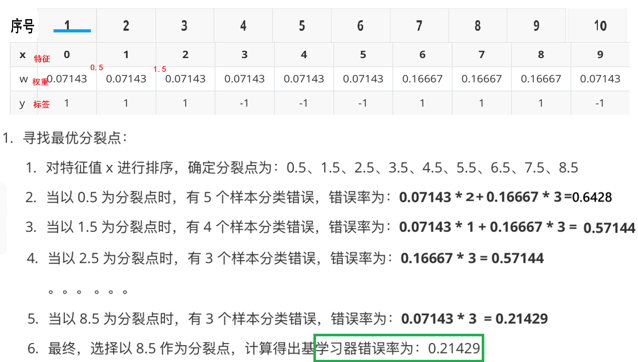
以此类推再去构建第三个分类器

最终得到一个强学习器

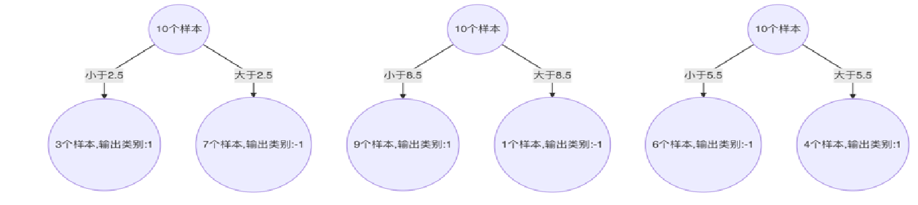
来个代码：

"""演示：adaboost算法 之葡萄酒案例adaboost算法介绍：属于boosting思想 ，即： 串行执行，每次使用全部样本，加权投票原理：1：使用全部样本 ，通过决策树模型（第1个弱分类器）进行训练，获取结果思路：预测正确-》权重下降预测错误-》权重上升2：把第1个弱分类器的处理结果，交给第2个弱分类进行训练，获取结果思路：预测正确-》权重下降预测错误-》权重上升3：以此类推，串行执行，直至最终获取结果
"""
import pandas as pd
from sklearn.preprocessing import LabelEncoder  # 标签编码器
from sklearn.model_selection import train_test_split  # 训练集、测试集分割
from sklearn.tree import DecisionTreeClassifier  # 决策树分类器
from sklearn.ensemble import AdaBoostClassifier  # AdaBoost分类器 -> 集成学习Boosting思想
from sklearn.metrics import accuracy_score  # 模型评估 -> 正确率
#1、获取数据集
df_wine=pd.read_csv("../data/wine0501.csv")
df_wine.info()
#2、数据预处理
# print(df['Class label'].unique())  # [1 2 3] 葡萄酒类别有3中 ，但是决策树CART树只能识别 二分类
# df_wine[df_wine['Class label']!=1]
#2.1 从标签列中 过滤标签1
df_wine=df_wine[df_wine['Class label']!=1] #过滤1类别   剩下2、3类别
#2.2 获取特征列 和标签列
x=df_wine[['Alcohol','Hue']]  #酒精  和  色泽
y=df_wine['Class label']     # 标签列
#2.3 打印一下
# print(x[:5])
# print(y[:5])
#2.4 通过标签编码器  2、3  标签编码器  0,1 [2,3]->[0,1]
le=LabelEncoder()
y=le.fit_transform(y)
# print(y)  #演示：标签编码器作用
#2.5 训练集和测试集切分
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=23,stratify=y)
#3、特征工程   此处略
#4、模型训练  预测  、评估
#场景一：单一决策树
#4.1 创建模型对象
es1=DecisionTreeClassifier(max_depth=3)
#4.2 训练模型
es1.fit(x_train,y_train)
#4.3模型预测
y_pre1=es1.predict(x_test)
print(f"单一决策树预测结果:{y_pre1}")
#4.4模型评估
print(f"单一模型预测正确率:{accuracy_score(y_test,y_pre1)}")
#场景2：adaboost -》集成学习 CART树   300棵
#4.1创建模型对象
#参1： 弱分类器（决策树对象）  参2：弱分类器个数 300   参3：学习率    参4：集成算法
es2=AdaBoostClassifier(estimator=es1,n_estimators=300,learning_rate=0.01,algorithm='SAMME.R')
#4.2
es2.fit(x_train,y_train)
#4.3模型预测
y_pre2=es2.predict(x_test)
print(f"Adaboost集成学习预测结果:{y_pre2}")
#4.4模型评估
print(f"Adaboost集成学习预测正确率:{accuracy_score(y_test,y_pre2)}")

提升树

引入残差概念

残差：真实值-预测值

预测某人的年龄为100岁

第1次预测：对100岁预测，预测成80岁；100 – 80 = 20（残差）

第2次预测：上一轮残差20岁作为目标值，预测成16岁；20 – 16 = 4 （残差）

第3次预测：上一轮的残差4岁作为目标值，预测成3.2岁；4 – 3.2 = 0.8（残差）

若三次预测的结果串联起来： 80 + 16 + 3.2 = 99.2

通过拟合残差可将多个弱学习器组成一个强学习器，这就是提升树的最朴素思想

梯度提升树

梯度提升树不再拟合残差，而是利用梯度下降的近似方法，利用损失函数的负梯度作为提升树算法中的残差近似值

GBDT 拟合的负梯度就是残差。如果我们的 GBDT 进行的是分类问题，则损失函数变为 logloss，此时拟合的目标值就是该损失函数的负梯度值

例子：

已知

初始化弱学习器

当模型预测值为何值时，会使得第一个弱学习器的平方误差最小，即：求损失函数对 f(xi) 的导数，并令导数为0

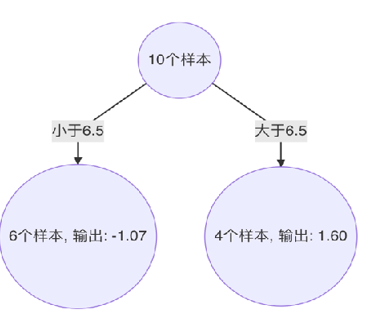
构建第一个弱学习器

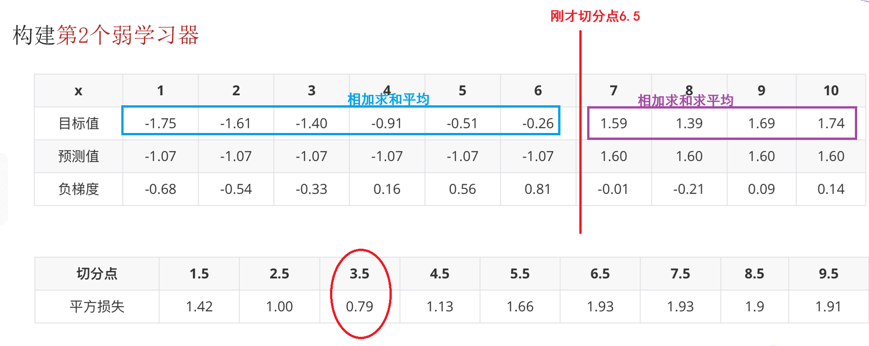
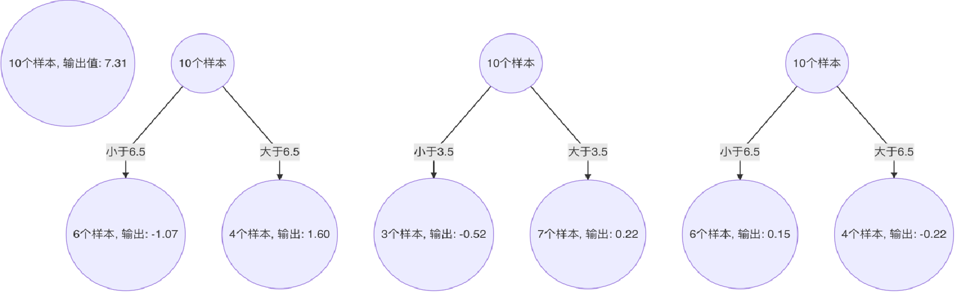
根据负梯度的计算方法得到下表：

当1.5为切分点：拟合负梯度-1.75, -1.61, -1.40, -0.91, … , 1.74

左子树：1个样本 -1.75， 右子树9个样本：-1.61，-1.40，-0.91…

右子树均值为：((-1.61) + (-1.40)+(-0.91)+(-0.51)+(-0.26)+1.59 +1.39 + 1.69 + 1.74 )/9=0.19；左子树均值为：- 1.75

计算平方损失：左子树0 + 右子树：(-1.61-0.19)*(-1.61-0.19)  + (-1.40-0.19)* (-1.40-0.19) + (-0.91-0.19)* (-0.91-0.19) + (-0.51-0.19)*(-0.51-0.19) +(-0.26-0.19)*(-0.26-0.19) +(1.59-0.19) *(1.59-0.19) + (1.39-0.19) *(1.39-0.19) + (1.69-0.19)*(1.69-0.19)  + (1.74-0.19) * (1.74-0.19)  =15.72308

•3 当 6.5 作为切分点时，平方损失最小，此时得到第1棵决策树

以3.5 作为切分点时，平方损失最小，此时得到第2棵决策树

构建最终弱学习器

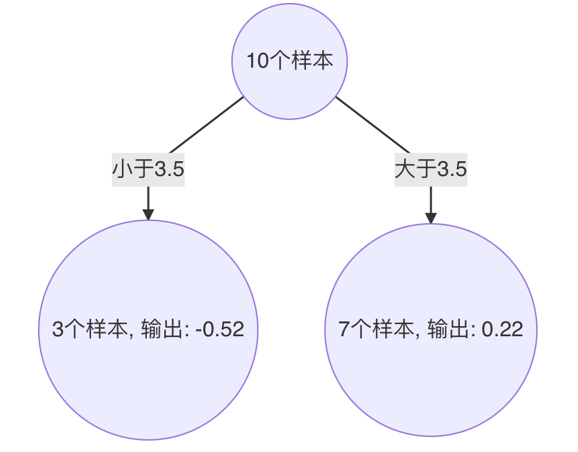
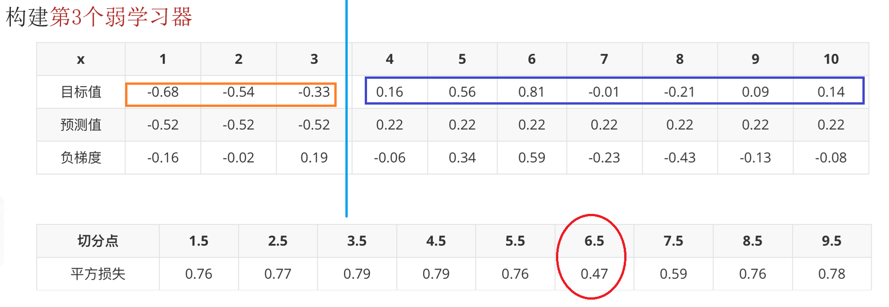
"""案例：演示：boosting 思想之GBDT  (梯度提升树) 处理泰坦尼克号案例GBDT: 梯度提升树解释：概述：通过拟合负梯度来获取一个强学习器流程：1：采用所有目标值的均值，作为第1个弱学习器的预测值 （初始化）2：目标值 -预测之 =负梯度（残差）该（列）值作为第2个弱学习器的 目标值3：针对于第1个弱学习器，依次计算每个分割点 的最小的平方和，找到最佳（）分割点。至此：第1个弱学习器搭建完毕4：把上述的分割点带入第2个弱学习，计算的预测值 = 以此分割点为界，目标值的均值，即为该部分预测值、5：计算第2个弱学习器的负梯度  最佳分割点 ，至此：第2个弱学习搭建完毕6：以此类推，直至程序结束
"""# 导入库
import pandas as pd
from sklearn.model_selection import train_test_split  # 切割训练集 和 测试集
from sklearn.tree import DecisionTreeClassifier  # 决策树分类器
from sklearn.ensemble import GradientBoostingClassifier  # 梯度提升树分类器
from sklearn.metrics import classification_report, accuracy_score  # 模型评估
from sklearn.model_selection import GridSearchCV  # 网格搜索# 1、读取数据
df = pd.read_csv("../data/train.csv")
df.info()
# 2、数据预处理
# 2.1提取特征和标签
x = df[['Pclass', 'Sex', 'Age']].copy()
y = df['Survived'].copy()# 2.2处理age
x['Age'] = x['Age'].fillna(x['Age'].mean())# 2.3热编码
x = pd.get_dummies(x)# 2.4 训练集 和 测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=18)# 3.特征工程# 4. 模型训练 预测 评估
# 场景1： 单个决策树 （CART）
# 4.1创建模型对象
es = DecisionTreeClassifier()# 4.2模型训练
es.fit(x_train, y_train)# 4.3模型预测
y_pre = es.predict(x_test)print(f"单个决策树对象预测结果:{y_pre}")# 4.4模型评估
print(f"单个决策树对象准确率:{accuracy_score(y_test, y_pre)}")# 场景2：梯度提升树对象（GBDT）
# 4.1创建模型对象
es2 = GradientBoostingClassifier()
# 4.2模型训练
es2.fit(x_train, y_train)
# 4.3模型预测
y_pre2 = es2.predict(x_test)
print(f"梯度提升树对象预测结果:{y_pre2}")# 4.4模型评估
print(f"梯度提升树对象准确率:{accuracy_score(y_test, y_pre2)}")# 场景3：针对GBDT模型，进行参数调优
param_dict = {'learning_rate': [0.3, 0.5, 0.8],'n_estimators': [50, 80, 120, 200],'max_depth': [3, 5, 7]
}
es3 = GradientBoostingClassifier()
es4=GridSearchCV(es3, param_dict,cv=2)
es4.fit(x_train,y_train)
print(f"网络搜索的模型准确率:{es4.best_score_}")
print(f"网格搜索和交叉验证后的模型参数:{es4.best_params_}")
print(f"网格搜索后的模型:{es4.best_estimator_}")

XGBoost

极端梯度提升树，集成学习方法的王牌

构建思想

1.构建模型的方法是最小化训练数据的损失函数

训练的模型复杂度较高，易过拟合。

2、在损失函数中加入正则化项

提高对未知的测试数据的泛化性能

XGBoost（Extreme Gradient Boosting）是对GBDT的改进，并且在损失函数中加入了正则化项

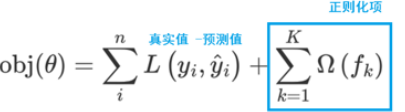
正则化项用来降低模型的复杂度

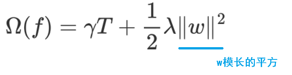
γT 中的 T 表示一棵树的叶子结点数量。

λ||w||2中的 w 表示叶子结点输出值组成的向量， ||w||是向量的模； λ是对该项的调节系数

怎么理解呢

emmm

假设我们要预测一家人对电子游戏的喜好程度，考虑到年轻和年老相比，年轻更可能喜欢电子游戏，以及男性和女性相比，男性更喜欢电子游戏，故先根据年龄大小区分小孩和大人，然后再通过性别区分开是男是女，逐一给各人在电子游戏喜好程度上打分：

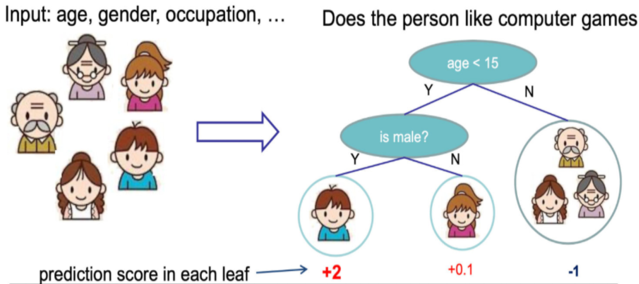
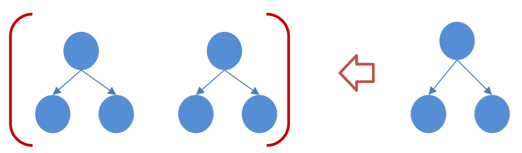
训练出tree1和tree2，类似之前gbdt的原理，两棵树的结论累加起来便是最终的结论

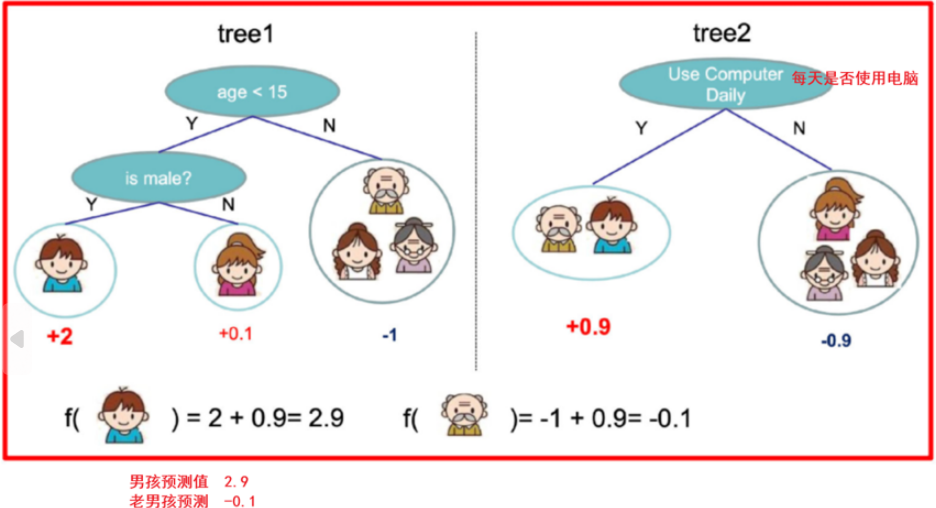
树tree1的复杂度表示为

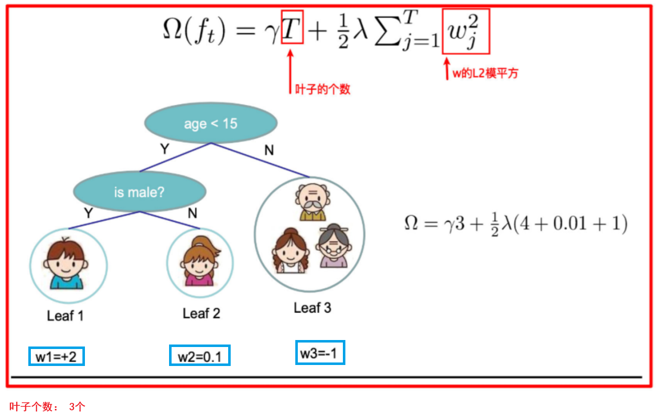
然后是XGBoost的推导过程，这个有点难

推导分析过程

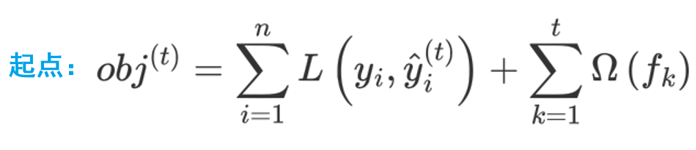
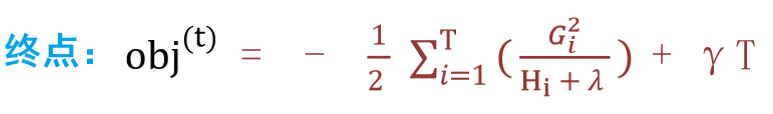
步骤：

1：在损失函数的基础上加上正则化项，要用到泰勒展开公式

2：基于泰勒展开进行转换，变为近似函数，还要转换问题角度

3：转换角度之后进行分析

4：得到最终结果，打分函数->Gain值越小越好

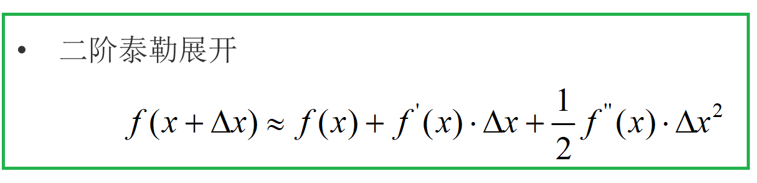
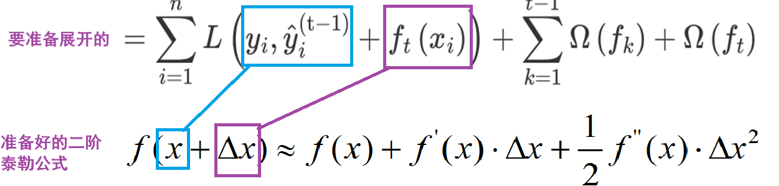
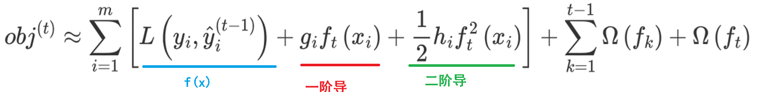
观察目标函数，发现以下两项表示t-1个弱学习器构成学习器的目标函数，都是常数，我们可以将其去掉

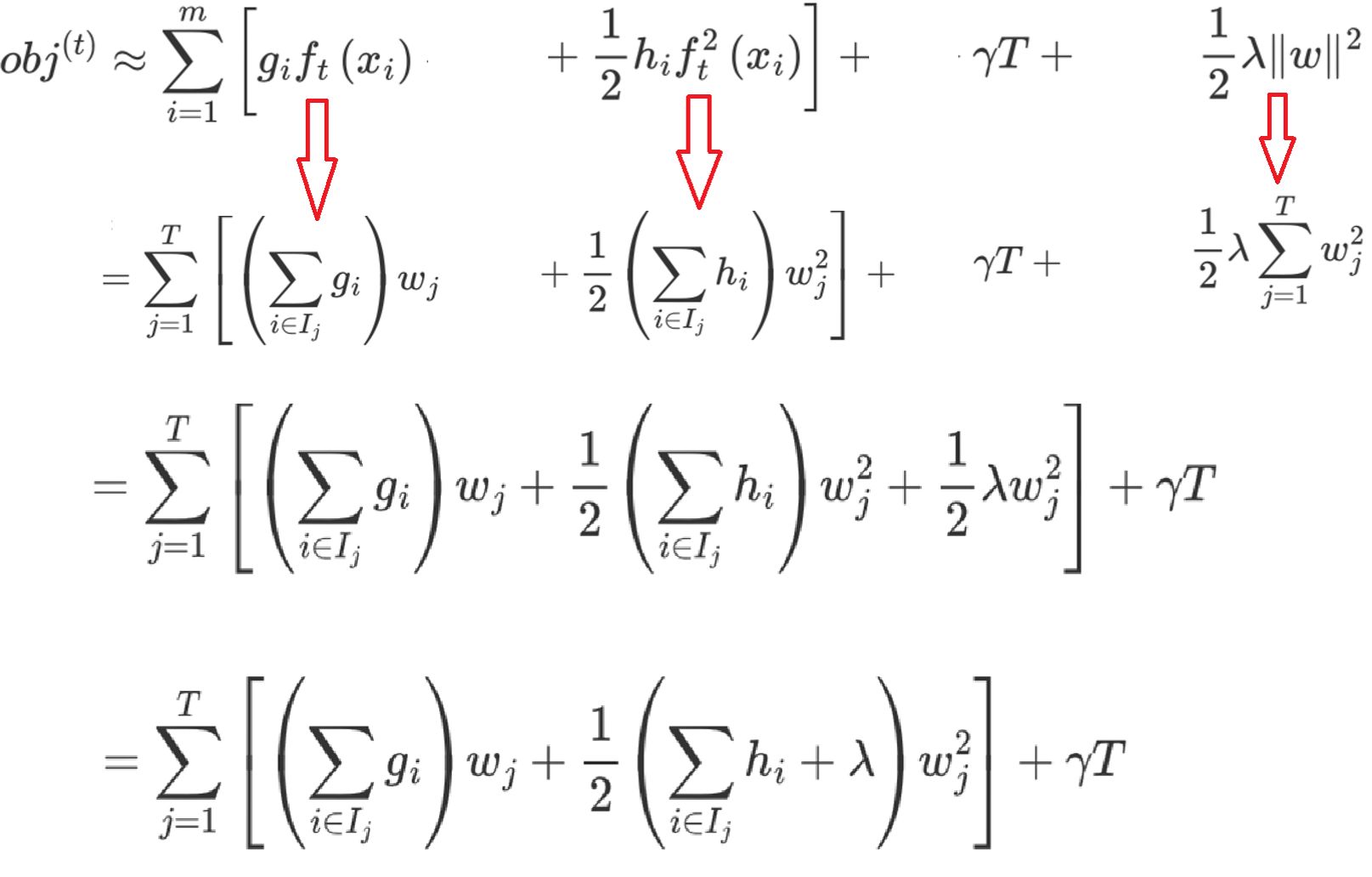
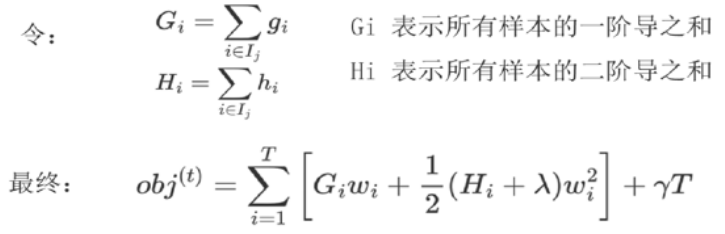求损失函数最小值，针对ωi进行求导

得到ωi之后我们代入原式

最终得到打分函数

会计算gain值来判断要不要分裂

来个小例子

计算10个样本在叶子节点上的输出表示

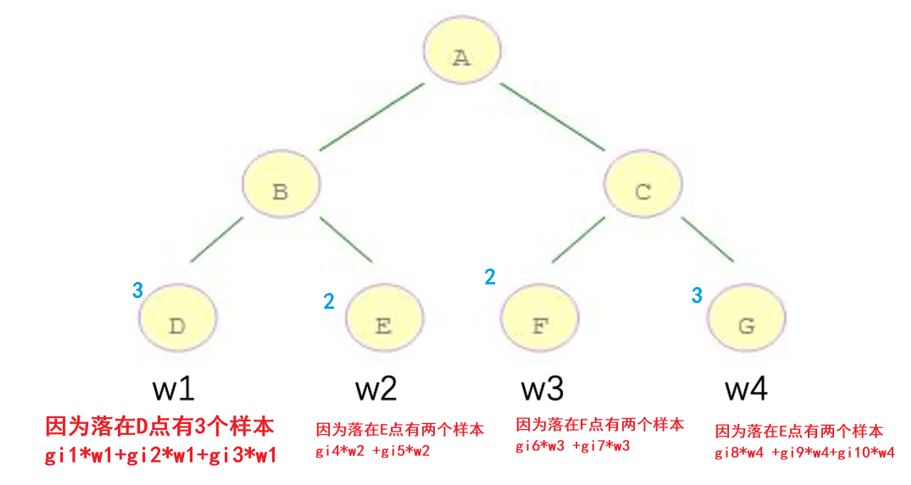
然后api的实现

import joblib  # 保存和加载模型
import numpy as np
import pandas as pd
import xgboost as xgb  # 极限梯度提升树对象
from collections import Counter  # 统计数据
from sklearn.model_selection import train_test_split, GridSearchCV  # 训练集和测试集的划分
from sklearn.metrics import classification_report, accuracy_score  # 模型(分类)评估报告
from sklearn.model_selection import StratifiedKFold  # 分层K折交叉验证, 类似于 网格搜索时 cv=折数
from sklearn.utils import class_weight  # 计算样本权重#1、定义函数 ，对红酒品质分类 -》 拆分 训练集 和 测试集   拆分后存储到CSV文件   [总csv] -》[训练集csv][测试集csv]
def dm01_data_split():#1、加载数据集df =pd.read_csv("../data/红酒品质分类.csv")#2、查看数据集# df.info()x=df.iloc[:,:-1]y=df.iloc[:,-1]-3  # 默认范围[3,8]  ->[0,5]# print(y)#3、数据是不均衡# print(f"{Counter(y)}")#4、切分训练集和测试集x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=23,stratify=y)#5、把上述的训练集特征 和标签数据拼接到一起  测试集特征 和标签数据拼接到一起pd.concat([x_train,y_train],axis=1).to_csv("../data/红酒品质分类_train.csv",index=False)  #忽略索引pd.concat([x_test, y_test], axis=1).to_csv("../data/红酒品质分类_test.csv", index=False)  # 忽略索引#2、定义函数  训练模型 并保存模型
def dm02_train_model():#1、读取训练集和测试集train_data=pd.read_csv("../data/红酒品质分类_train.csv")test_data=pd.read_csv("../data/红酒品质分类_test.csv")#2、提取训练集和测试集特征数据和标签数据x_train = train_data.iloc[:,:-1]y_train=train_data.iloc[:,-1]x_test = test_data.iloc[:, :-1]y_test = test_data.iloc[:, -1]#3、创建模型对象es=xgb.XGBClassifier(max_depth=5 , # 树的最大深度n_estimators=100,  #树的数量learning_rate=0.1, #学习率random_state=24, #随机种子objective='multi:softmax'  #多分类问题，使用多分类模型)#加入平衡权重 ，因为数据集是样本不均衡#参1：平衡权重#参2：标签数据（即：参考标签数据分布，平衡权重）cw=class_weight.compute_sample_weight("balanced",y_train)#4、模型训练es.fit(x_train,y_train,sample_weight=cw)#5、模型评估print(f"准确率:{es.score(x_test,y_test)}")#6、模型保存joblib.dump(es,"../model/红酒品质分类.pkl")print("模型保存成功")#3、定义函数 ，测试模型
def dm03_use_model():#1、读取训练集和测试集train_data=pd.read_csv("../data/红酒品质分类_train.csv")test_data=pd.read_csv("../data/红酒品质分类_test.csv")#2、提取训练集和测试集特征数据和标签数据x_train = train_data.iloc[:,:-1]y_train=train_data.iloc[:,-1]x_test = test_data.iloc[:, :-1]y_test = test_data.iloc[:, -1]#3、加载模型es=joblib.load("../model/红酒品质分类.pkl")#4、创建网络搜索+交叉验证（结合分层采样数据）param_dict={'max_depth' :[3,5,8,10,12],  # 树的最大深度'n_estimators' : [100,130,150,180,230],  # 树的数量'learning_rate' : [0.1,0.3,0.5,1.0,1.2]  # 学习率}#创建分层采样对象#参1：折数（cv）  参2：是否打乱数据  参3：随机种子skf=StratifiedKFold(n_splits=2,shuffle=True,random_state=23)#创建网格搜索ge_es=GridSearchCV(es,param_dict,cv=skf)ge_es.fit(x_train,y_train)y_pre=ge_es.predict(x_test)print(f"预测值为：{y_pre}")print(f"准确率:{accuracy_score(y_test,y_pre)}")print(f"最优估计器{ge_es.best_estimator_}")print(f"最优评分:{ge_es.best_score_}")if __name__ == '__main__':dm01_data_split()dm02_train_model()dm03_use_model()