2.链表算法
2.1 常见算法题
-
1. 合并两个有序链表
-
2. 分隔链表
-
3. 合并 K 个升序链表
-
4. 删除链表的倒数第 N 个结点
-
5. 链表的中间结点
-
6. 环形链表 I 、环形链表 II
-
7. 相交链表
这些解法都用到了双指针技巧,对于单链表相关的题目,双指针的运用是非常广泛的。
2.2 经典习题
-
8. 删除排序链表中的重复元素 II
-
9. 有序矩阵中第 K 小的元素
-
10. 查找和最小的 K 对数字
-
11. 两数相加、两数相加 II
2.3 花式翻转
反转单链表的迭代解法不是一个困难的事情,但是递归实现就有点难度了。如果再加一点难度,仅仅反转单链表中的一部分,是否能够同时用迭代和递归实现呢?再进一步,如果 k 个一组反转链表,阁下又应如何应对?
-
12. 反转链表
对于「分解问题」思路的递归算法,最重要的就是明确递归函数的定义。具体来说,我们的 reverseList 函数定义是这样的:输入一个节点 head,将「以 head 为起点」的链表反转,并返回反转之后的头结点。
不要跳进递归(你的脑袋能压几个栈呀?),而是要根据刚才的函数定义,来弄清楚递归代码会产生什么结果:

这个 reverseList(head.next) 执行完成后,整个链表就成了这样:
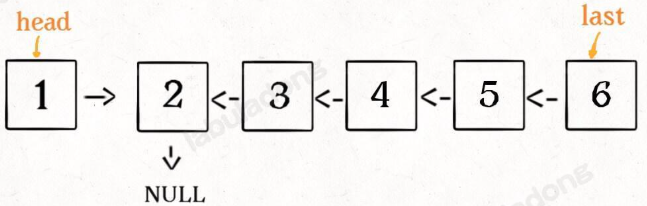
有两个地方需要注意:
- 递归函数要有 base case,意思是如果链表为空或者只有一个节点的时候,反转结果就是它自己,直接返回即可。
- 当链表递归反转之后,新的头结点是 last,而之前的 head 变成了最后一个节点,别忘了链表的末尾要指向 null。
❤️
递归操作链表的效率不如迭代
值得一提的是,递归操作链表并不高效。
递归解法和迭代解法相比,时间复杂度都是 O(N),但是迭代解法的空间复杂度是 O(1),而递归解法需要堆栈,空间复杂度是 O(N)。
所以递归操作链表可以用来练习递归思维,但是考虑效率的话还是使用迭代算法更好。
-
13. 反转链表 II
-
14. K 个一组翻转链表
总结:
递归的思想相对迭代思想,稍微有点难以理解,处理的技巧是:不要跳进递归,而是利用明确的定义来实现算法逻辑。
处理看起来比较困难的问题,可以尝试化整为零,把一些简单的解法进行修改,解决困难的问题。
2.4 回文链表
- 寻找回文串的核心思想是从中心向两端扩展。
- 而判断一个字符串是不是回文串就简单很多,不需要考虑奇偶情况,只需要双指针技巧,从两端向中间逼近即可。
-
15. 回文链表
最简单的办法就是,把原始链表反转存入一条新的链表,然后比较这两条链表是否相同。
优化后就是 先找到中间节点,翻转半部分链表再遍历对比。
2.2 常用技巧
- 「虚拟头节点」技巧:也就是dummy节点,当需要创造一条新的链表(并非是 new 一个)的时候,可以使用虚拟头结点简化边界情况的处理。如果不用就需要特判指针为 null 的情况去处理。
- 「快慢双指针」技巧:利用 fast、slow 指针,可以是 fast 先移动,也可以是同时移动,fast 每次移动多步,用 fast、slow 两个指针的状态或者位置来达到某个目标。
在题 6 链表判环中,fast 与 slow 相遇则有环,利用了两个指针的状态;
在题 5 寻找中间节点中,fast 走到终点,则表示 slow 走到中间,利用了两个指针的位置关系。
- 「链表分解」技巧:链表的分解技巧可以运用到很多单链表题目中,题目并不一定明确地要求你把链表分解成两部分,只要要求你从链表筛选出若干节点,都可以用这个技巧。
题 8 删除排序链表中的重复元素,就可以理解为 一条链表存放不重复的节点,另一条链表存放重复的节点
- 「多路归并」技巧:是指将多个有序序列合并成一个有序序列的算法技术。问题本质:有 K 个有序序列;需要将它们合并成一个有序序列;关键:每次选择当前所有序列中最小的元素,有些时候题目没有明确给出 K 个有序序列,但可以转化。使用优先队列(最小堆)来维护各个序列的当前最小元素,每次取出堆顶元素,然后将该元素所在序列的下一个元素加入堆中。
题 3、9、10 都可以用「多路归并」技巧解答,先将题目数据转化为 k 个有序序列,再结合优先队列维护最小堆,直接获取所需数据。
- 「虚拟链表」技巧:多用于将数组虚拟化为链表,逻辑上当链表来使用,如将二维问题转化为链表合并问题,在「多路归并」相关题目中使用较多。过程中还需「索引维护」以及「边界控制」等细节设计。
- 「分解问题」思路:如果问题有子问题结构,即可以转化为树形结构,那么可以用递归来求解子问题。
题 13、14 的反转链表就可以分解为子问题,不直接操作当前节点,而是反转子链表,然后与当前节点拼接,处理交给递归即可,定义好递归函数,以及 base case。
