当前位置：首页 > news >正文

老题新解|同行列对角线的格

news 2025/9/8 7:18:57

《信息学奥赛一本通》第99题：同行列对角线的格

题目描述
输入三个自然数 $N$ ， $i$ ， $j$ （ $\le i \le n$ ， $\le j \le n$ ），输出在一个 $\times N$ 格的棋盘中（行列均从 $1$ 开始编号），与格子 $(i$ ， $j)$ 同行、同列、同一对角线的所有格子的位置。
如： $n = 4$ ， $i = 2$ ， $j = 3$ 表示了棋盘中的第二行第三列的格子，
当 $n = 4$ ， $i = 2$ ， $j = 3$ 时，输出的结果是： $(2, 1) (2, 2) (2, 3) (2, 4)$ 同一行上格子的位置。
$(1, 3) (2, 3) (3, 3) (4, 3)$ 同一列上格子的位置。
$(1, 2) (2, 3) (3, 4)$ 左上到右下对角线上的格子的位置。
$(4, 1) (3, 2) (2, 3) (1, 4)$ 左下到右上对角线上的格子的位置。
输入格式
一行，三个自然数 $N$ ， $i$ ， $j$ ，相邻两个数之间用单个空格隔开 $\le N \le 10)$ 。
输出格式
第一行：从左到右输出同一行格子位置；
第二行：从上到下输出同一列格子位置；
第三行：从左上到右下输出同一对角线格子位置；
第四行：从左下到右上输出同一对角线格子位置。
其中每个格子位置用如下格式输出： $(x, y)$ ， $x$ 为行号， $y$ 为列号，采用英文标点，中间无空格。相邻两个格子位置之间用单个空格隔开。
输入输出样例 #1
输入 #1
4 2 3
输出 #1
(2,1) (2,2) (2,3) (2,4)
(1,3) (2,3) (3,3) (4,3)
(1,2) (2,3) (3,4)
(4,1) (3,2) (2,3) (1,4)

大家好，我是莫小特。
这篇文章给大家带来《信息学奥赛一本通》中的第99题：同行列对角线的格。

一、题目描述

洛谷的题号是：B2100 同行列对角线的格

二、题意分析

这道题是信息学奥赛一本通练习题的第 99 题。

根据输入格式的描述，输入有三个自然数，包含 N、i、j，数据范围： $\le N \le 10)$ ，使用 int 类型。

int N;
cin>>N;

接下来分析题意，根据题目意思，需要按要求输出相应的格式。

输出的第一行从左到右输出同一行格子的位置，也就是第 i 行所有格子的位置，第 i 行的特点是行的数据相同，而列的位置从 1 遍历到 N，使用 for 循环实现列的输出，注意输出时，将括号加上，最后一个括号要加上空格。

for(int a=1;a<=N;a++)
{cout<<"("<<i<<","<<a<<") ";	
}

接下来需要换行，再输出下一组数据。

cout<<endl;

第二行从上到下输出同一列格子位置，具有的特点是：列相同，而行从 1 遍历到 N。

for(int b=1;b<=N;b++)
{cout<<"("<<b<<","<<j<<") ";	
}

换行，之后再输出第三行。

第三行的要求是，从左上到右下输出同一对角线格子位置，具体的规则如下图，研究发现如果是对角线的话，行和列的值都相等。

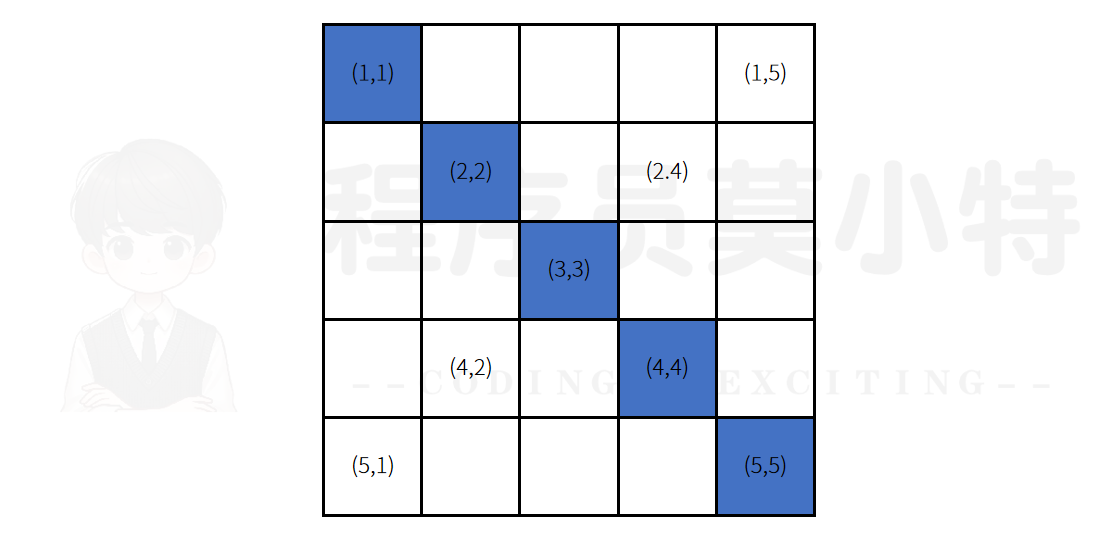
但如果是其他行的话，研究发现，行和列相减等于一个固定值，也就是： $i - j$ ，可以画出下图，对其进行分析。

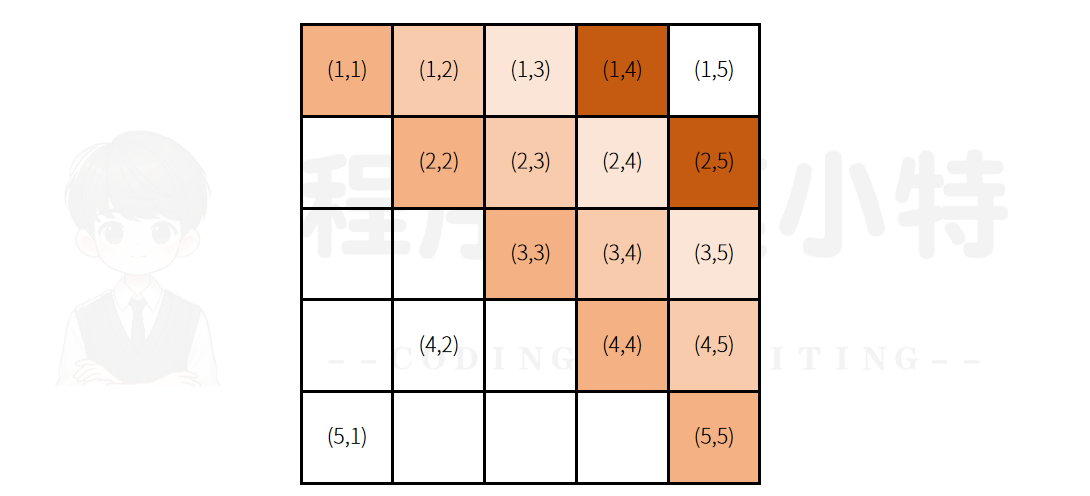
所以代码可写：

for(int c=1;c<=N;c++)
{for(int d=1;d<=N;d++){if(c-d==i-j){cout<<"("<<c<<","<<d<<") ";}}
}
cout<<endl;//一定要加换行

换行之后，来研究第四行：从左下到右上输出同一对角线格子位置，要注意哦，是从左下到右上，需要用倒序实现。

而行列的关系是，行和列相加等于一个固定值。

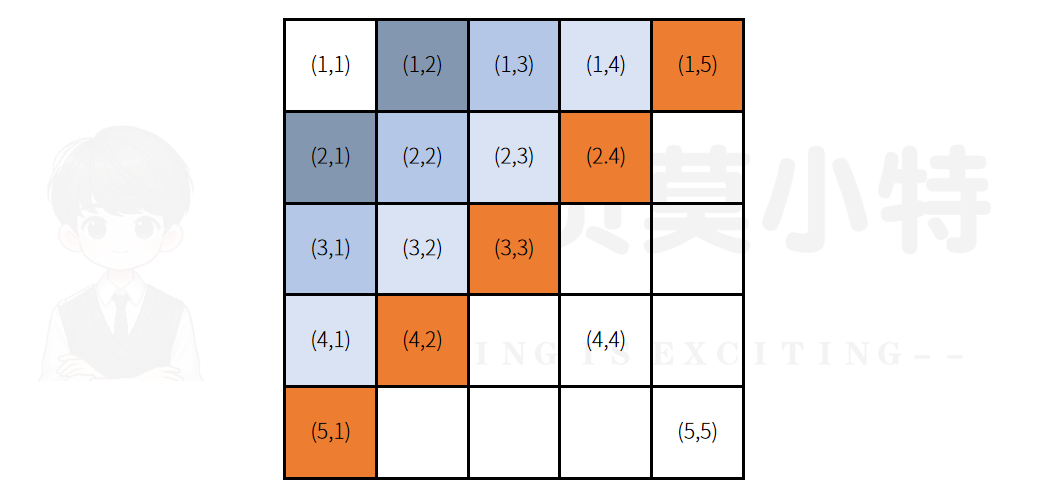
代码可写：

for(int c=N;c>=1;c--)
{for(int d=1;d<=N;d++){if(c+d==i+j){cout<<"("<<c<<","<<d<<") ";}}
}

按照样例输入数据，验证一下。

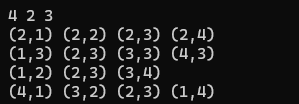
数据验证正确，提交到网站测评。

验证通过~

三、完整代码

该题的完整代码如下：

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int main()
{int N,i,j;cin>>N>>i>>j;for(int a=1;a<=N;a++){cout<<"("<<i<<","<<a<<") ";	} cout<<endl;for(int b=1;b<=N;b++){cout<<"("<<b<<","<<j<<") ";	} cout<<endl;for(int c=1;c<=N;c++){for(int d=1;d<=N;d++){if(c-d==i-j){cout<<"("<<c<<","<<d<<") ";}}} cout<<endl;for(int c=N;c>=1;c--){for(int d=1;d<=N;d++){if(c+d==i+j){cout<<"("<<c<<","<<d<<") ";}}}return 0;
}