九.弗洛伊德(Floyd)算法

弗洛伊德算法

佛洛依德(Floyd)算法介绍

1）和Dijkstra算法一样，弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一，1978年图灵奖获得者，斯坦福大学计算机科学系教授罗伯特.弗洛伊德命名

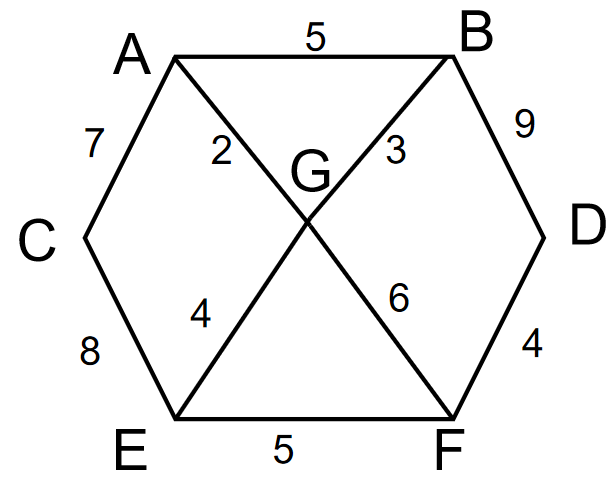
2）弗洛伊德算法(Floyd)计算图中各个顶点之间的最短路径，比如以A顶点为出发顶点到其他六个顶点的最短路径是多少，紧接着又会以B这个顶点为出发顶点，求出从B这个顶点到其他六个顶点的最短路径，依此类推

3）迪杰斯特拉算法用于计算图中某一个顶点到其他顶点的最短路径。

4）弗洛伊德算法VS迪杰斯特拉算法：迪杰斯特拉算法是选一个顶点，求出这个顶点到其他顶点的最短路径；而弗洛伊德算法是把每个顶点都看作出发顶点(比如有七个顶点，七个顶点都会依次作为出发顶点)，求出每个顶点到其他顶点的最短路径

弗洛伊德(Floyd)算法图解分析

1）设置顶点vi到顶点vk的最短路径已知为Lik (L表示Length, i表示i顶点， k表示k顶点), 顶点vk到vj的最短路径已知为Lkj , 顶点vi到vj的路径为Lij ,则vi到vj的最短路径为：

min((Lik+Lkj),Lij)，vk的取值为图中所有顶点，则可获得vi到vj的最短路径。

2）至于vi到vk的最短路径Lik或者vk到vj的最短路径Lkj，是以同样的方式获得的

i——k——j (i这个顶点通过k这个顶点到达j这个顶点) Lik+Lkj=Lij

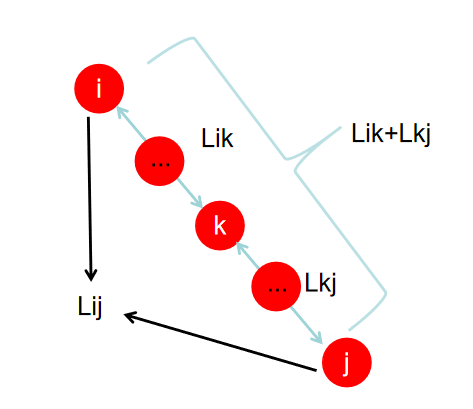
i——j (也有可能i和j是直接可以连通) Lij

通过比较才能知道i到j的最短路径是哪个，如果Lij小，则最短路径是Lij，如果Lik+Lkj小(也就是通过这个中间顶点到达的距离更小，就把这个和记为最短路径)，则最短路径为Lik+Lkj

3）弗洛伊德(Floyd)算法图解分析—举例说明

自己跟自己相连距离为0，N代表不可直连

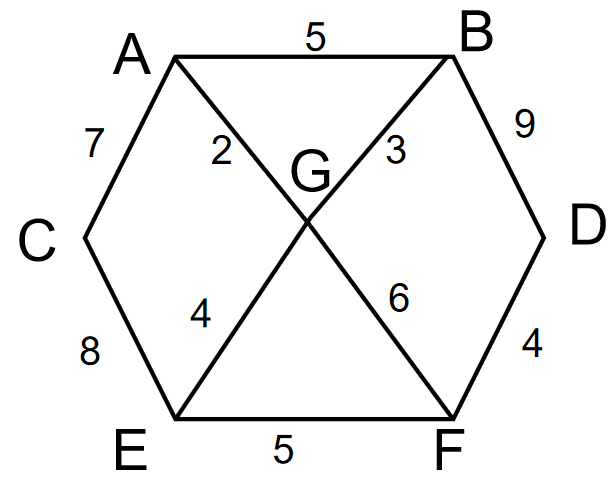
初始顶点前驱关系：

第一轮循环中，以A(下标为0)作为中间顶点

即把A作为中间顶点的所有情况都进行遍历，在遍历的过程中更新距离表和前驱关系表

将A作为中间顶点情况有

1. C—A—G [距离9]
2. C—A—B [距离12]
3. G—A—B [距离7]

距离表和前驱关系表更新为

第二轮循环中，以B(下标为:1)作为中间节点

第三轮循环中，以C(下标为:2)作为中间节点,依此类推

中间顶点 [A,B,C,D,E,F,G] k=0, 1, 2, 3, 4, 5, 6

出发顶点 [A,B,C,D,E,F,G] i=0, 1, 2, 3, 4, 5, 6

终点 [A,B,C,D,E,F,G] j=0, 1, 2, 3, 4, 5, 6

这里用到了三层for循环，最后得到每一个顶点到其他顶点的最短距离，最后的结果在距离表里面

弗洛伊德(Floyd)算法最佳应用—最短路径

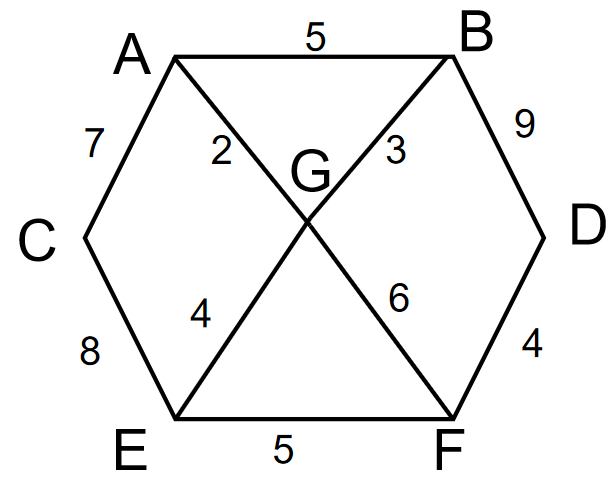
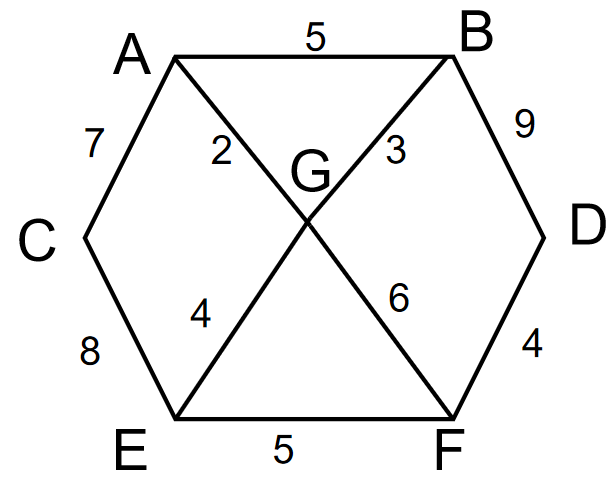
1）胜利乡有7个村庄(A, B, C, D, E, F, G)

2. 各个村庄的距离用边线表示(权)，比如A—B距离5公里

3）问：如何计算出各村庄到其他各村庄的最短距离？

代码实现

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;namespace Floyd
{class FloydAlgorithm{static void Main(string[] args){//测试图是否创建成功char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };  //  顶点数组//创建邻接矩阵int[,] matrix = new int[vertex.Length, vertex.Length];int N = 65535;  //表示不可直连matrix = new int[,]{{0,5,7,N,N,N,2 },{5,0,N,9,N,N,3 },{7,N,0,N,8,N,N },{N,9,N,0,N,4,N },{N,N,8,N,0,5,4 },{N,N,N,4,5,0,6 },{2,3,N,N,4,6,0 },};//创建图对象Grap grap = new Grap(vertex.Length, matrix, vertex);//调用弗洛伊德算法grap.floyd();grap.show();}}//创建图class Grap{//属性char[] vertex;  //存放顶点的数组private int[,] dis;  //距离表:从各个顶点出发到其他顶点的距离，最后的结果，也是保留在该数组private int[,] pre;  //保存到达目标顶点的前驱顶点//构造器/// <summary>/// /// </summary>/// <param name="length">顶点的个数</param>/// <param name="matrix">邻接矩阵</param>/// <param name="vertex">顶点数组</param>public Grap(int length,int[,] matrix,char[] vertex){this.vertex = vertex;this.dis = matrix;this.pre = new int[length, length];//对pre数组进行初始化,注意存放的是前驱节点的下标for (int i = 0; i < length; i++){for (int j = 0; j < length; j++){pre[i, j] = i;}}}//显示pre数组和dis数组public void show(){//先将pre数组输出for (int i = 0; i < vertex.Length; i++){for (int j = 0; j < vertex.Length; j++){Console.Write(vertex[pre[i,j]]+"  ");}Console.WriteLine();//将dis数组输出for (int j = 0; j < vertex.Length; j++){Console.Write("("+vertex[i]+"到"+vertex[j]+"的最短距离为"+dis[i,j]+")");}Console.WriteLine();Console.WriteLine();}}//弗洛伊德算法,比较容易理解，而且容易实现public void floyd(){int len;  //变量保存距离// 对中间顶点遍历，k就是中间顶点的下标 [A,B,C,D,E,F,G]for (int k = 0; k < vertex.Length; k++)   {//从i顶点开始出发[A,B,C,D,E,F,G]for (int i = 0; i < vertex.Length; i++){//从i顶点出发，经过k中间顶点，到达j顶点,j是这次的终点[A,B,C,D,E,F,G]for (int j = 0; j < vertex.Length; j++){len = dis[i, k] + dis[k, j];   //求出从i顶点出发，经过k中间顶点，到达j顶点的距离if (len < dis[i, j]) //如果len小于dis[i,j]直连距离{dis[i, j] = len;  //更新距离pre[i, j] = pre[k, j];   //更新前驱顶点}//如果len>dis[i,j]，我就不动}}}}}
}

代码运行结果

A A A F G G A
(A到A的最短距离为0)(A到B的最短距离为5)(A到C的最短距离为7)(A到D的最短距离为12)(A到E的最短距离为6)(A到F的最短距离为8)(A到G的最短距离为2)

B B A B G G B
(B到A的最短距离为5)(B到B的最短距离为0)(B到C的最短距离为12)(B到D的最短距离为9)(B到E的最短距离为7)(B到F的最短距离为9)(B到G的最短距离为3)

C A C F C E A
(C到A的最短距离为7)(C到B的最短距离为12)(C到C的最短距离为0)(C到D的最短距离为17)(C到E的最短距离为8)(C到F的最短距离为13)(C到G的最短距离为9)

G D E D F D F
(D到A的最短距离为12)(D到B的最短距离为9)(D到C的最短距离为17)(D到D的最短距离为0)(D到E的最短距离为9)(D到F的最短距离为4)(D到G的最短距离为10)

G G E F E E E
(E到A的最短距离为6)(E到B的最短距离为7)(E到C的最短距离为8)(E到D的最短距离为9)(E到E的最短距离为0)(E到F的最短距离为5)(E到G的最短距离为4)

G G E F F F F
(F到A的最短距离为8)(F到B的最短距离为9)(F到C的最短距离为13)(F到D的最短距离为4)(F到E的最短距离为5)(F到F的最短距离为0)(F到G的最短距离为6)

G G A F G G G
)(D到G的最短距离为10)

G G E F E E E
(E到A的最短距离为6)(E到B的最短距离为7)(E到C的最短距离为8)(E到D的最短距离为9)(E到E的最短距离为0)(E到F的最短距离为5)(E到G的最短距离为4)

G G E F F F F
(F到A的最短距离为8)(F到B的最短距离为9)(F到C的最短距离为13)(F到D的最短距离为4)(F到E的最短距离为5)(F到F的最短距离为0)(F到G的最短距离为6)

G G A F G G G
(G到A的最短距离为2)(G到B的最短距离为3)(G到C的最短距离为9)(G到D的最短距离为10)(G到E的最短距离为4)(G到F的最短距离为6)(G到G的最短距离为0)