pytorch非线性回归
一、线性回归回顾
1.1 线性回归回顾
在上两篇文章中,我们简单了解了线性回归训练逻辑,其中有这样一段矩阵定义:
- 输入矩阵(特征矩阵)
X=[x1x2…xn] \begin{gather*} X = \begin{bmatrix} x_1 & x_2 & \dots & x_n \end{bmatrix} \end{gather*} X=[x1x2…xn]
- XXX转置得到XTX^TXT,XTX^TXT增加一列全为1得到X′X'X′
X′=[x11x21…1xn1] \begin{gather*} X' = \begin{bmatrix} x_1 & 1\\ x_2 & 1\\ \dots & 1\\ x_n & 1 \end{bmatrix} \end{gather*} X′=x1x2…xn1111
- 权重偏置矩阵
W=[kb] \begin{gather*} W = \begin{bmatrix} k \\ b \end{bmatrix} \end{gather*} W=[kb]
- 目标向量矩阵
Y=[y1y2…yn] \begin{gather*} Y = \begin{bmatrix} y_1 \\ y_2 \\ \dots \\ y_n \end{bmatrix} \end{gather*} Y=y1y2…yn
- 预测值向量
Y′=X′⋅W=[x11x21…1xn1][kb]=[kx1+bkx2+b…kxn+b] \begin{gather*} Y' = X' \cdot W = \begin{bmatrix} x_1 & 1\\ x_2 & 1\\ \dots & 1\\ x_n & 1 \end{bmatrix} \begin{bmatrix} k \\ b \end{bmatrix} = \begin{bmatrix} kx_1+b \\ kx_2+b\\ \dots\\ kx_n+b \end{bmatrix} \end{gather*} Y′=X′⋅W=x1x2…xn1111[kb]=kx1+bkx2+b…kxn+b
- 损失函数
L(k,b)=1n∣Y′−Y∣2 \begin{gather*} L(k, b) = \frac{1}{n} |Y'-Y|^2 \end{gather*} L(k,b)=n1∣Y′−Y∣2
如果我们对上述式子稍微修改一下,把权重和偏置分开,做如下定义:
- 权重
W=[kk⋮k] \begin{gather*} W = \begin{bmatrix} k \\ k \\ \vdots \\ k \end{bmatrix} \end{gather*} W=kk⋮k
- 预测值向量(注意偏置b是标量),我们改为更通用的符号Y^\hat{Y}Y^表示
Y^=X⋅W+b=[x1x2…xn][kk⋮k]+b=[kx1+bkx2+b…kxn+b] \begin{gather*} \hat{Y} = X \cdot W + b = \begin{bmatrix} x_1 & x_2 & \dots & x_n \end{bmatrix} \begin{bmatrix} k \\ k \\ \vdots \\ k \end{bmatrix} + b = \begin{bmatrix} kx_1+b \\ kx_2+b \\ \dots \\ kx_n+b \end{bmatrix} \end{gather*} Y^=X⋅W+b=[x1x2…xn]kk⋮k+b=kx1+bkx2+b…kxn+b
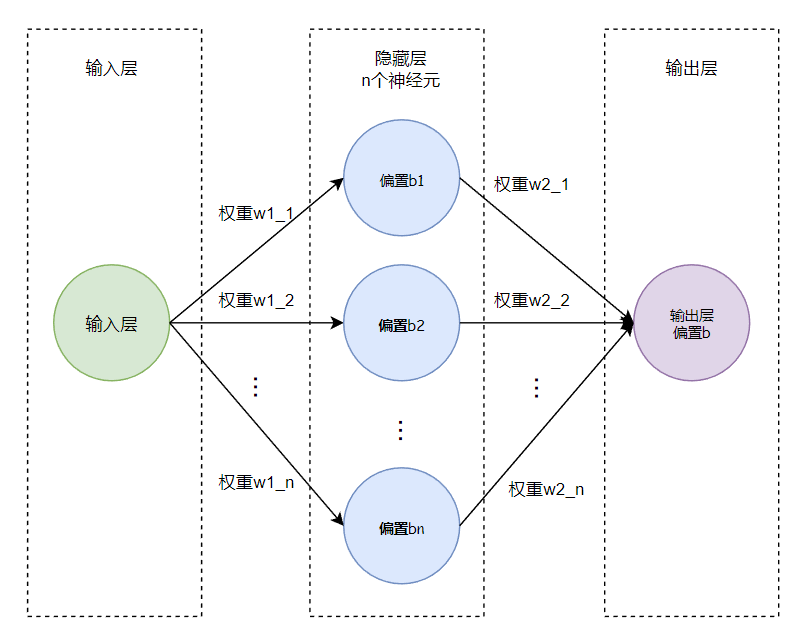
以一维特征输入(即一个特征值)、一个n神经元隐藏层的模型为例,可用如下图表示:
如果是多维特征输入(假设有m个特征值,每个特征值有n个样本),则有:
Y^=X⋅W+b=[x11x12…x1nx21x22…x2n⋮⋮⋮⋮xm1xm2…xmn][k1k2…kmk1k2…km⋮⋮⋮⋮k1k2…km]+b=[k1x11+bk1x12+b…k1x1n+bk2x21+bk2x22+b…k2x2n+b⋮⋮⋮⋮kmxm1+bkmxm2+b…kmxmn+b] \begin{gather*} \hat{Y} = X \cdot W + b = \begin{bmatrix} x_{11} & x_{12} & \dots & x_{1n} \\ x_{21} & x_{22} & \dots & x_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ x_{m1} & x_{m2} & \dots & x_{mn} \\ \end{bmatrix} \begin{bmatrix} k_1 & k_2 & \dots & k_m \\ k_1 & k_2 & \dots & k_m \\ \vdots & \vdots & \vdots & \vdots \\ k_1 & k_2 & \dots & k_m \\ \end{bmatrix} + b = \begin{bmatrix} k_1x_{11}+b & k_1x_{12}+b & \dots & k_1x_{1n}+b \\ k_2x_{21}+b & k_2x_{22}+b & \dots & k_2x_{2n}+b \\ \vdots & \vdots & \vdots & \vdots \\ k_mx_{m1}+b & k_mx_{m2}+b & \dots & k_mx_{mn}+b \\ \end{bmatrix} \end{gather*} Y^=X⋅W+b=x11x21⋮xm1x12x22⋮xm2……⋮…x1nx2n⋮xmnk1k1⋮k1k2k2⋮k2……⋮…kmkm⋮km+b=k1x11+bk2x21+b⋮kmxm1+bk1x12+bk2x22+b⋮kmxm2+b……⋮…k1x1n+bk2x2n+b⋮kmxmn+b
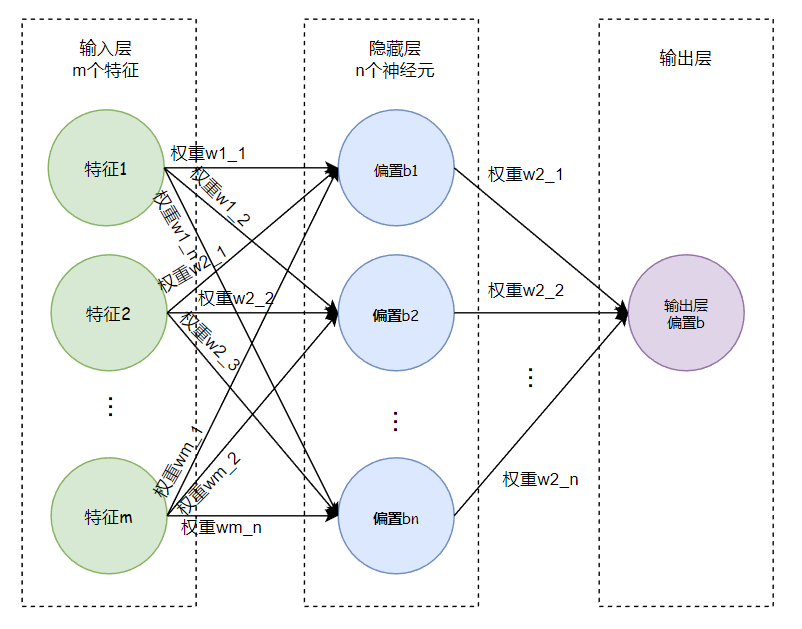
1.2 偏置共享与偏置独立
细心的读者会发现,在上述多维特征输入时,所有特征共用一个偏置b,但是按一维特征输入场景来推理来说,应该每个特征都有一个偏置bib_ibi。一个偏置(b=b1+b2+⋯+bnb = b_1+b_2+\dots+b_nb=b1+b2+⋯+bn)与多个偏置有什么差异呢?我们以二维输入特征来简单分析下:
- 模型定义
我们现在有两个不同的模型:
1、共享偏置模型:y^=w1∗x1+w2∗x2+b\hat{y} = w₁*x₁ + w₂*x₂ + by^=w1∗x1+w2∗x2+b
2、独立偏置模型:y^=w1∗x1+b1+w2∗x2+b2\hat{y} = w₁*x₁ + b₁ + w₂*x₂ + b₂y^=w1∗x1+b1+w2∗x2+b2
- 梯度设计
假设我们使用均方误差作为损失函数:1n∣Y^−Y∣2\frac{1}{n} |\hat{Y}-Y|^2n1∣Y^−Y∣2
1、共享偏置模型的梯度计算
对于y^=w1∗x1+w2∗x2+b\hat{y} = w₁*x₁ + w₂*x₂ + by^=w1∗x1+w2∗x2+b:
1)∂L∂w1=(y^−y)∗∂y^∂w1=(y^−y)∗x1\frac{\partial L}{\partial w_1}=(\hat{y}-y)*\frac{\partial \hat{y}}{\partial w_1}=(\hat{y}-y)*x_1∂w1∂L=(y^−y)∗∂w1∂y^=(y^−y)∗x1
2)∂L∂w2=(y^−y)∗∂y^∂w2=(y^−y)∗x2\frac{\partial L}{\partial w_2}=(\hat{y}-y)*\frac{\partial \hat{y}}{\partial w_2}=(\hat{y}-y)*x_2∂w2∂L=(y^−y)∗∂w2∂y^=(y^−y)∗x2
3)∂L∂b=(y^−y)∗∂y^∂b=(y^−y)∗1\frac{\partial L}{\partial b}=(\hat{y}-y)*\frac{\partial \hat{y}}{\partial b}=(\hat{y}-y)*1∂b∂L=(y^−y)∗∂b∂y^=(y^−y)∗1
关键点:偏置b只有一个梯度项,它直接反映整个模型的误差。
2、独立偏置模型的梯度计算
对于y^=w1∗x1+b1+w2∗x2+b2\hat{y} = w₁*x₁ + b1 + w₂*x₂ + b2y^=w1∗x1+b1+w2∗x2+b2
1)∂L∂w1=(y^−y)∗∂y^∂w1=(y^−y)∗x1\frac{\partial L}{\partial w_1}=(\hat{y}-y)*\frac{\partial \hat{y}}{\partial w_1}=(\hat{y}-y)*x_1∂w1∂L=(y^−y)∗∂w1∂y^=(y^−y)∗x1
2)∂L∂w2=(y^−y)∗∂y^∂w2=(y^−y)∗x2\frac{\partial L}{\partial w_2}=(\hat{y}-y)*\frac{\partial \hat{y}}{\partial w_2}=(\hat{y}-y)*x_2∂w2∂L=(y^−y)∗∂w2∂y^=(y^−y)∗x2
3)∂L∂b1=(y^−y)∗∂y^∂b1=(y^−y)∗1\frac{\partial L}{\partial b_1}=(\hat{y}-y)*\frac{\partial \hat{y}}{\partial b_1}=(\hat{y}-y)*1∂b1∂L=(y^−y)∗∂b1∂y^=(y^−y)∗1
4)∂L∂b2=(y^−y)∗∂y^∂b2=(y^−y)∗1\frac{\partial L}{\partial b_2}=(\hat{y}-y)*\frac{\partial \hat{y}}{\partial b_2}=(\hat{y}-y)*1∂b2∂L=(y^−y)∗∂b2∂y^=(y^−y)∗1
关键点:每个特征有自己的偏置梯度,但这两个梯度完全相同。
- 参数更新
使用梯度下降法,参数更新规则为:参数=参数−学习率×∂L∂∂参数参数 = 参数 - 学习率 × \frac {\partial L}{\partial ∂}参数参数=参数−学习率×∂∂∂L参数
1、共享偏置模型的更新
1)w1=w1−α∗(y^−y)∗x1w_1 = w_1 - \alpha * (\hat{y}-y) * x_1w1=w1−α∗(y^−y)∗x1
2)w2=w2−α∗(y^−y)∗x2w_2 = w_2 - \alpha * (\hat{y}-y) * x_2w2=w2−α∗(y^−y)∗x2
3)b=b−α∗(y^−y)b = b - \alpha * (\hat{y}-y)b=b−α∗(y^−y)
2、独立偏置模型的更新
1)w1=w1−α∗(y^−y)∗x1w_1 = w_1 - \alpha * (\hat{y}-y) * x_1w1=w1−α∗(y^−y)∗x1
2)w2=w2−α∗(y^−y)∗x2w_2 = w_2 - \alpha * (\hat{y}-y) * x_2w2=w2−α∗(y^−y)∗x2
3)b1=b1−α∗(y^−y)b_1 = b_1 - \alpha * (\hat{y}-y)b1=b1−α∗(y^−y)
4)b2=b2−α∗(y^−y)b_2 = b_2 - \alpha * (\hat{y}-y)b2=b2−α∗(y^−y)
- 分析与比较
1、数学等价性
如果我们令 b = b₁ + b₂,那么两个模型在数学上是完全等价的:
y^=w1∗x1+b1+w2∗x2+b2=w1∗x1+w2∗x2+(b1+b2)=w1∗x1+w2∗x2+b\hat{y} = w_1*x_1+b_1+w_2*x_2+b_2 = w_1*x_1+w_2*x_2+(b_1+b_2) = w_1*x_1+w_2*x_2+by^=w1∗x1+b1+w2∗x2+b2=w1∗x1+w2∗x2+(b1+b2)=w1∗x1+w2∗x2+b
这意味着两个模型有相同的表达能力,但独立偏置模型多了一个冗余参数。
2、优化过程的影响
虽然两个模型最终能学习到相同的函数,但它们的优化过程有所不同:
1)收敛速度:独立偏置模型有两个偏置参数接收相同的梯度信号,这相当于给偏置项分配了双倍的学习能力。在某些情况下,这可能加快收敛速度,但也可能导致 overshooting(超调)。
2)参数初始化:在独立偏置模型中,b₁和b₂需要分别初始化。如果它们的初始值不同,优化路径会与共享偏置模型不同。
3)正则化影响:如果使用L1或L2正则化,独立偏置模型会对两个偏置项分别施加正则化惩罚,而共享偏置模型只对一个偏置项施加惩罚。
3、实际训练中的表现
在实践中,共享偏置模型通常更优,因为:
1)参数效率:共享偏置模型使用更少的参数达到相同的效果,降低了过拟合风险。
2)优化稳定性:共享偏置模型的优化过程更加直接和稳定。
3)可解释性:共享偏置模型的结果更容易解释,因为偏置有一个明确的全局意义。
所以总结起来就是使用共享偏置(一个神经元一个标量b)在梯度计算和优化过程中是完全可行且通常更优的:
1)梯度计算:共享偏置的梯度计算简单直接,不会带来任何问题。
2)优化效率:共享偏置模型参数更少,训练更高效,泛化能力更好。
3)数学等价:独立偏置模型只是共享偏置模型的一种冗余表示,没有增加实际表达能力。
1.2 线性回归的局限性
假设现在有个线性模型f(x)=w1∗x+b1f(x)=w_1*x+b_1f(x)=w1∗x+b1,还有另外一个隐含层线性模型g(x)=w2∗x+b2g(x)=w_2*x+b_2g(x)=w2∗x+b2,则:
g(f(x))=w2∗f(x)+b2=w2∗(w1∗x+b1)+b2=w1∗w2∗x+w2b1+b2 g(f(x))=w_2*f(x)+b_2=w_2*(w_1*x+b_1)+b_2=w_1*w_2*x+w_2b_1+b_2 g(f(x))=w2∗f(x)+b2=w2∗(w1∗x+b1)+b2=w1∗w2∗x+w2b1+b2
如果令w=w1∗w2,b=w2b1+b2w=w_1*w_2,b=w_2b_1+b_2w=w1∗w2,b=w2b1+b2,则有:
g(f(x))=w∗x+b g(f(x))=w*x+b g(f(x))=w∗x+b
这个式子说明线性模型无论叠加多少层,最终的输出仍然是输入的一个线性组合,只不过权重矩阵变成了各层权重矩阵的连乘。这和一个没有隐藏层的线性模型在表达能力上没有任何本质区别。而现实世界中的绝大多数问题(如图像识别、语音识别、自然语言处理)都是高度非线性的,一个线性模型无法描绘这些复杂的数据分布。
二、非线性回归
2.1 激活函数
为了解决线性模型无法拟合复杂的非线性数据问题,于是考虑引入一个非线性函数,也就是激活函数,使得神经元变成如下形式:
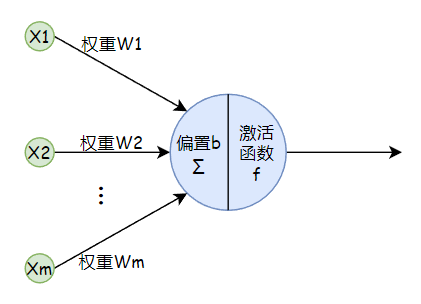
如果有多个隐藏层,一般每个隐藏层都有激活函数:
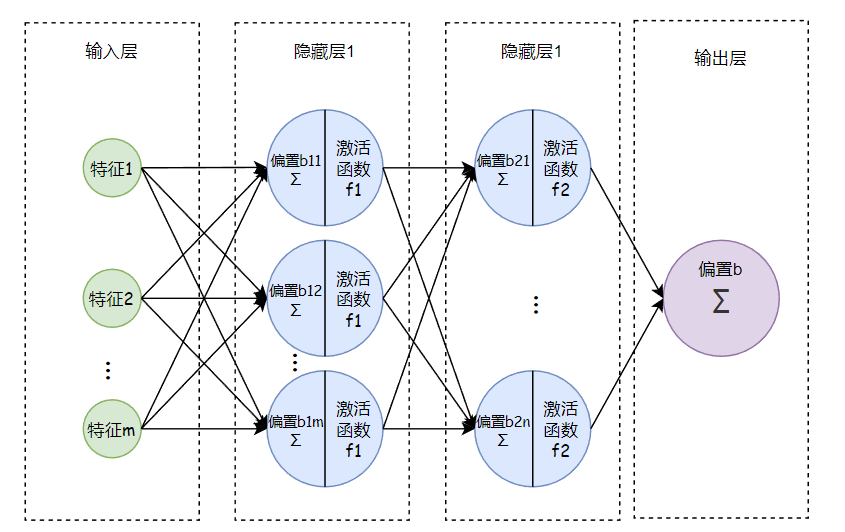
激活函数通常是一些简单的非线性函数,常见的激活函数有:
2.1.1 S型(Sigmoid)函数族
- Sigmoid (Logistic函数)
公式:f(x)=11+e−xf(x) = \frac{1}{1 + e^{-x}}f(x)=1+e−x1
值域:(0, 1)
导数: f′(x)=f(x)⋅(1−f(x))f'(x) = f(x) \cdot (1 - f(x))f′(x)=f(x)⋅(1−f(x))
优点:输出平滑,易于求导;输出可解释为概率(例如,用于二分类的输出层)。
缺点:梯度消失:当输入值的绝对值很大时,函数会进入饱和区,梯度接近于0。在反向传播时,梯度会不断相乘,导致浅层网络的梯度变得极小,权重无法有效更新;输出非零中心:输出恒为正,这会导致梯度更新时,权重向量的更新方向被束缚,优化路径呈锯齿状,降低收敛效率;涉及指数运算,计算较慢。
用途:二分类任务的输出层。
- Tanh (双曲正切函数)
公式: f(x)=ex−e−xex+e−x=2⋅sigmoid(2x)−1f(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} = 2 \cdot \text{sigmoid}(2x) - 1f(x)=ex+e−xex−e−x=2⋅sigmoid(2x)−1
值域:(-1, 1)
导数: f′(x)=1−(f(x))2f'(x) = 1 - (f(x))^2f′(x)=1−(f(x))2
优点:零中心:输出以0为中心,收敛速度通常比Sigmoid快。
缺点:同样存在梯度消失问题。
用途:在RNN(如LSTM、GRU)等模型中仍有应用,但现在在CNN的隐藏层中较少使用。
2.2.2 ReLU (Rectified Linear Unit) 家族
- ReLU
公式: f(x)=max(0,x)f(x) = \max(0, x)f(x)=max(0,x)
值域:[0, +∞)
导数:f′(x)={1if x>0 0if x≤0f'(x) = \begin{cases} 1 & \text{if } x > 0 \ 0 & \text{if } x \leq 0 \end{cases}f′(x)={1if x>0 0if x≤0
优点:有效缓解梯度消失:在正区间,梯度恒为1,彻底解决了梯度饱和问题;计算速度极快:只需比较和取最大值,没有指数等复杂运算;符合生物稀疏性:使得网络中的部分神经元输出为0,增加了网络的稀疏性,可能带来更好的表征能力。
缺点:Dying ReLU (死亡ReLU) 问题:一旦输入为负,梯度为0,神经元将永远无法被激活,相应的权重也无法更新;输出非零中心。
用途:绝大多数CNN和深度前馈网络的默认选择。
- Leaky ReLU (带泄露ReLU)
公式: f(x)={xif x>0 αxif x≤0f(x) = \begin{cases} x & \text{if } x > 0 \ \alpha x & \text{if } x \leq 0 \end{cases}f(x)={xif x>0 αxif x≤0 (其中 α\alphaα 是一个很小的常数,如0.01)
优点:有效缓解梯度消失:在正区间,梯度恒为1,彻底解决了梯度饱和问题;计算速度极快:只需比较和取最大值,没有指数等复杂运算;符合生物稀疏性:使得网络中的部分神经元输出为0,增加了网络的稀疏性,可能带来更好的表征能力。
缺点:Dying ReLU (死亡ReLU) 问题:一旦输入为负,梯度为0,神经元将永远无法被激活,相应的权重也无法更新;输出非零中心。
用途:绝大多数CNN和深度前馈网络的默认选择。
- Parametric ReLU (PReLU,参数化ReLU)
说明:Leaky ReLU的进阶版。它将负区间的斜率 α\alphaα 作为一个可学习的参数,让网络在训练过程中自己学习最优的斜率。
优点:比Leaky ReLU更灵活,性能可能更好。
缺点:引入了额外的参数。
- Exponential Linear Unit (ELU,指数线性单元)
公式: f(x)={xif x>0 α(ex−1)if x≤0f(x) = \begin{cases} x & \text{if } x > 0 \ \alpha(e^x - 1) & \text{if } x \leq 0 \end{cases}f(x)={xif x>0 α(ex−1)if x≤0
值域:[-α, +∞)
优点:负区域平滑,比Leaky ReLU更能缓解死亡ReLU问题;输出更接近零中心化,可能使学习 dynamics 更稳定。
缺点:涉及指数运算,计算量比ReLU稍大。
2.2.3 其他新兴激活函数
- Swish
公式: f(x)=x⋅sigmoid(βx)f(x) = x \cdot \text{sigmoid}(\beta x)f(x)=x⋅sigmoid(βx) (谷歌大脑提出,β\betaβ 可以是常数或可学习参数)
特点:平滑、非单调:在负区间不是完全平坦的,有一个小小的“凸起”;在实践中,尤其在非常深的网络中(如Transformer),其性能经常优于 ReLU;可被视为一种自门控机制(sigmoid 部分像一个自动学习的门,控制让多少原始输入 xxx 通过)。
用途:在许多现代架构中逐渐成为ReLU的有力竞争者。
- GELU (Gaussian Error Linear Unit)
公式: f(x)=x⋅Φ(x)f(x) = x \cdot \Phi(x)f(x)=x⋅Φ(x),其中 Φ(x)\Phi(x)Φ(x) 是标准正态分布的累积分布函数。常用近似实现:0.5x⋅(1+tanh[2π(x+0.044715x3)])0.5x \cdot (1 + \text{tanh}[\sqrt{\frac{2}{\pi}}(x + 0.044715x^3)])0.5x⋅(1+tanh[π2(x+0.044715x3)])
特点:与Swish类似,也是平滑且非单调的;被用于BERT、GPT等最先进的Transformer模型中,效果显著;其设计思想是基于随机正则化的理念,可以理解为“根据输入的大小,以一定的概率随机决定是否激活神经元”。
2.3 激活函数在前向传播和反向传播过程中的作用
2.3.1 在前向传播中的作用
前向传播是数据从输入层流向输出层的过程,目的是为了得到网络的预测结果,激活函数在前向传播中的核心作用就是引入非线性变换,塑造网络的表达能力。
1、加权求和
首先,每个神经元会计算其所有输入的加权和(加上偏置项):
z=(w1∗x1+w2∗x2+...+wn∗xn)+b z = (w1 * x1 + w2 * x2 + ... + wn * xn) + b z=(w1∗x1+w2∗x2+...+wn∗xn)+b
这一步是线性的。如果网络只做这一步,那么无论堆叠多少层,整个网络仍然等价于一个单层线性模型,无法学习复杂模式。
2、激活变换
然后,这个线性结果 z 被送入激活函数 f(.):
a=f(z)
a = f(z)
a=f(z)
这一步是非线性的。正是这个非线性函数 f 打破了线性限制,使得神经网络能够学习并模拟极其复杂的非线性关系。
2.3.2 在反向传播中的作用
反向传播是误差从输出层反向流回输入层的过程,目的是计算每个参数(权重 w 和偏置 b)对于总误差的“贡献”有多大(即梯度),以便后续用梯度下降法进行更新。
核心作用:提供梯度(导数),并控制误差信号如何反向流动。
反向传播的核心算法是链式法则。激活函数在这里扮演着梯度调节器的关键角色。
我们来看一下误差是如何通过一个神经元反向传播的。假设对于某个神经元,我们已知从它后面层反传回来的误差信号是 ∂Loss∂a\frac{\partial Loss}{\partial a}∂a∂Loss
1、计算误差关于加权输入 z 的梯度
根据链式法则,误差对线性输出 z 的梯度为:
∂Loss∂z=∂Loss∂a∗∂a∂z \frac{\partial Loss}{\partial z} = \frac{\partial Loss}{\partial a} * \frac{\partial a}{\partial z} ∂z∂Loss=∂a∂Loss∗∂z∂a
其中:
∂Loss∂a\frac{\partial Loss}{\partial a}∂a∂Loss:是从下一层反传回来的误差信号。
∂a∂z\frac{\partial a}{\partial z}∂z∂a:这就是激活函数在点 z 处的导数 f’(z)。
2、关键点
激活函数的导数 f’(z) 直接作为一个乘数因子,调节了反传回来的误差信号∂Loss∂a\frac{\partial Loss}{\partial a}∂a∂Loss的大小:
如果 f’(z) 很大(例如 ReLU 在正区的导数为1),误差信号可以几乎无损地传递回去。
如果 f’(z) 很小(例如 Sigmoid 在饱和区的导数接近0),误差信号经过这里后会急剧缩小。
3、继续反向传播
得到∂Loss∂a\frac{\partial Loss}{\partial a}∂a∂Loss后,我们就可以进一步计算误差对权重 w 和偏置 b 的梯度了:
∂Loss∂a=∂Loss∂z∗∂z∂w=∂Loss∂z∗x \frac{\partial Loss}{\partial a} = \frac{\partial Loss}{\partial z} * \frac{\partial z}{\partial w} = \frac{\partial Loss}{\partial z} * x ∂a∂Loss=∂z∂Loss∗∂w∂z=∂z∂Loss∗x
∂Loss∂b=∂Loss∂z∗∂z∂b=∂Loss∂z∗1 \frac{\partial Loss}{\partial b} = \frac{\partial Loss}{\partial z} * \frac{\partial z}{\partial b} = \frac{\partial Loss}{\partial z} * 1 ∂b∂Loss=∂z∂Loss∗∂b∂z=∂z∂Loss∗1
因此,激活函数的导数 f’(z) 是误差反向传播的“阀门”。它的大小直接决定了误差信号能有多少传递回更早的层,从而影响权重更新的幅度。梯度消失/爆炸问题很大程度上是由激活函数的导数特性决定的。
三、非线性回归实战
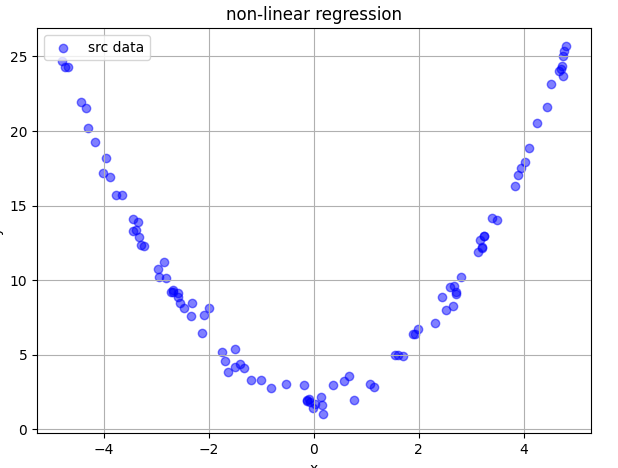
3.1 数据准备
基于$ y = x^2+2+\delta 初始化数据,其中初始化数据,其中初始化数据,其中\delta$是噪音:
def generate_data(n_samples=100, noise_std=0.5):x = np.random.uniform(-5, 5, n_samples)y = x ** 2 + 2 + np.random.normal(0, noise_std, n_samples) # 标准差为noise_std(默认0.5)的高斯噪声return x, y# [-5, 5]内生成100组数据,并转换成pytorch张量
x, y = generate_data()
x_tensor = torch.tensor(x, dtype=torch.float32).view(-1, 1)
y_tensor = torch.tensor(y, dtype=torch.float32).view(-1, 1)
3.2 非线性回归模型定义
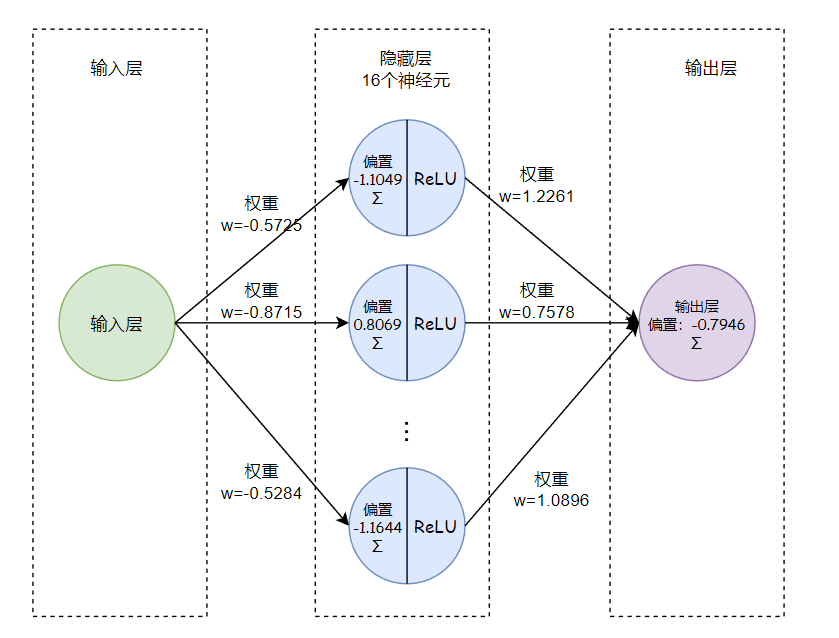
由于数据比较简单,我们把数据设置为一个隐藏层,该隐藏层有16个神经元(隐藏层数量和每层神经元个数可以根据结果适当调整),激活函数使用ReLU,模型逻辑如下:
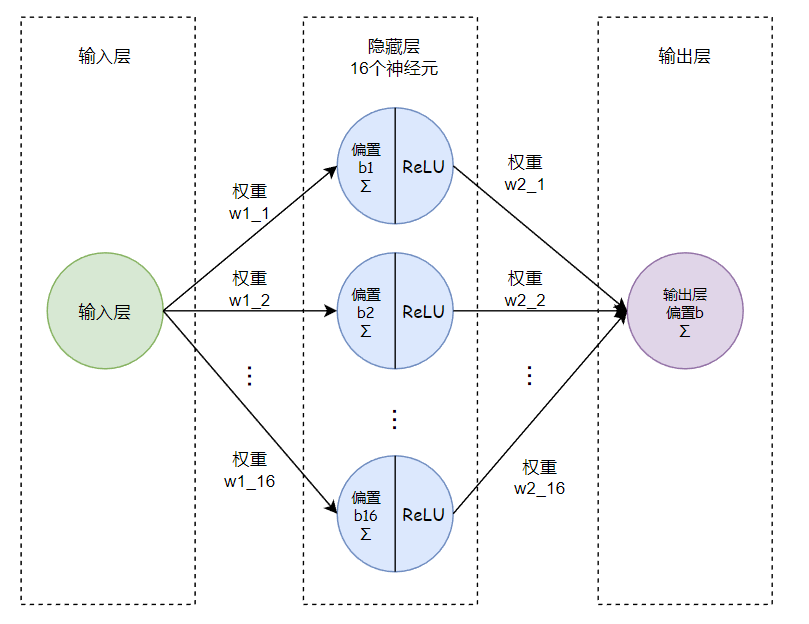
代码定义:
class NonlinearRegressionModel(nn.Module):def __init__(self, hidden_size=16):super(NonlinearRegressionModel, self).__init__()self.fc1 = nn.Linear(1, hidden_size) # 输入层->隐藏层,1个特征值->16个神经元self.fc2 = nn.Linear(hidden_size, 1) # 隐藏层->输出层,16个神经元->1个输出self.relu = nn.ReLU() # 激活函数# 反向传播定义def forward(self, x):x = self.relu(self.fc1(x)) # 输入层->隐藏层->激活函数ReLUx = self.fc2(x) # 输出层return x
3.2 训练
损失函数使用均方差,优化器采用随机梯度下降:
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-2)
再定义训练函数:
def train(x_tensor, y_tensor, model, optimizer, epochs=10000):global lossfor epoch in range(epochs):output = model(x_tensor)loss = criterion(output, y_tensor) # 损失函数计算optimizer.zero_grad() # 梯度清零loss.backward() # 反向传播optimizer.step() # 更新优化器权重和偏置print("model.parameters:", list(model.parameters()))print("loss", loss)
训练:
model = NonlinearRegressionModel()
train(x_tensor, y_tensor, model, optimizer)
根据训练好的模型生成预测数据:
with torch.no_grad():x_plot = torch.linspace(-5, 5, 100).view(-1, 1)y_pred = model(x_plot).numpy()
绘制原始数据、模型预测数据:
def draw_srs_data(x, y, x_plot, y_pred):plt.subplot(1, 2, 1)plt.scatter(x, y, alpha=0.5, label='src data', color='blue')# plt.plot(x, x ** 2 + 2, 'r-', label='real data(no noise)', linewidth=2)plt.plot(x_plot.numpy(), y_pred, 'g-', label='model predict', linewidth=2)plt.xlabel('x')plt.ylabel('y')plt.title('non-linear regression')plt.legend()plt.grid(True)
完整代码:
# non_linear.py
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as pltdef generate_data(n_samples=100, noise_std=0.5):x = np.random.uniform(-5, 5, n_samples)y = x ** 2 + 2 + np.random.normal(0, noise_std, n_samples)return x, yclass NonlinearRegressionModel(nn.Module):def __init__(self, hidden_size=16):super(NonlinearRegressionModel, self).__init__()self.fc1 = nn.Linear(1, hidden_size)self.fc2 = nn.Linear(hidden_size, 1)self.relu = nn.ReLU()def forward(self, x):x = self.relu(self.fc1(x))x = self.fc2(x)return xdef draw_srs_data(x, y, x_plot, y_pred):plt.subplot(1, 2, 1)plt.scatter(x, y, alpha=0.5, label='src data', color='blue')# plt.plot(x, x ** 2 + 2, 'r-', label='real data(no noise)', linewidth=2)plt.plot(x_plot.numpy(), y_pred, 'g-', label='model predict', linewidth=2)plt.xlabel('x')plt.ylabel('y')plt.title('non-linear regression')plt.legend()plt.grid(True)def train(x_tensor, y_tensor, model, optimizer, epochs=10000):global lossfor epoch in range(epochs):output = model(x_tensor)loss = criterion(output, y_tensor)optimizer.zero_grad()loss.backward()optimizer.step()print("model.parameters:", list(model.parameters()))print("loss", loss)x, y = generate_data()
x_tensor = torch.tensor(x, dtype=torch.float32).view(-1, 1)
y_tensor = torch.tensor(y, dtype=torch.float32).view(-1, 1)model = NonlinearRegressionModel()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-2)
train(x_tensor, y_tensor, model, optimizer)with torch.no_grad():x_plot = torch.linspace(-5, 5, 100).view(-1, 1)y_pred = model(x_plot).numpy()plt.figure(figsize=(12, 5))
draw_srs_data(x, y, x_plot, y_pred)plt.tight_layout()
plt.show()
3.3 结果
执行python non_linear.py,得到如下结果图:
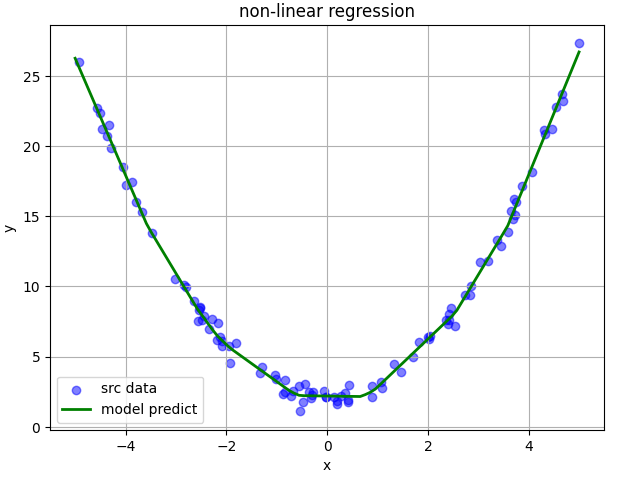
控制台会有如下输出:
r$ python non_linear.py
model.parameters: [Parameter containing:
tensor([[-0.5725],[-0.8715],[-0.6000],[ 0.4226],[ 0.3406],[ 0.7297],[ 1.1236],[ 0.8047],[-0.6204],[-0.6497],[-1.0850],[-0.8127],[ 1.3206],[ 0.9978],[-0.8070],[-0.5284]], requires_grad=True), Parameter containing:
tensor([-1.1049, 0.8069, 0.5919, -1.5139, 0.6573, 0.3944, 0.8038, -2.8824,-1.6015, -1.4321, -0.5863, -2.8985, -0.8921, -2.5376, 0.7211, -1.1644],requires_grad=True), Parameter containing:
tensor([[1.2261, 0.7578, 0.5869, 1.3730, 0.5185, 0.6679, 0.9325, 2.7502, 1.6487,1.4138, 0.9142, 2.8944, 1.2952, 2.5416, 0.9316, 1.0896]],requires_grad=True), Parameter containing:
tensor([-0.7946], requires_grad=True)]
loss tensor(0.2001, grad_fn=<MseLossBackward0>)
从控制台的输出可以看出,得到的模型损失值为0.2001,对应的模型为: